Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС

1. Лекция по учебной дисциплине «Цифровая схемотехника и обработка сигналов» (Д-0205-1) Тема № 9: «Описание ЛДС в частотной

ВОЕННАЯ АКАДЕМИЯ СВЯЗИ
Лекция
по учебной дисциплине «Цифровая схемотехника и обработка
сигналов»
(Д-0205-1)
Тема № 9: «Описание ЛДС в частотной области»
Занятие № 29: «Частотные характеристики ЛДС»
Руководитель занятия – доцент кафедры, к.т.н., доцент,
полковник Филимонов Василий Александрович
г. Санкт-Петербург
2018

2. Учебные цели:

2
Учебные цели:
Изучить частотные характеристики
ЛДС, их свойства и порядок расчёта.
2.
Изучить
влияние
параметров
передаточных функций на частотные
характеристики.
1.
Кафедра №2, ВАС

3. Учебные вопросы:

3
Учебные вопросы:
1. Определение
и
свойства
частотных характеристик ЛДС.
2. Вычисление
частотных
характеристик.
3. Взаимосвязь
между
характеристиками ЛДС.
Кафедра №2, ВАС

4. Литература для самостоятельной работы обучаемых:

4
Литература для самостоятельной работы обучаемых:
1. 1. Цифровая обработка сигналов. Краткий курс/ Д. А.
Улахович – СПб.: ВАС, 2017. – 408 с. (стр. 88-99).
2. Цифровая обработка сигналов./ Авторы: Д. А. Улахович
/ Электронное учеб. пособие /– СПб.: ВАС, 2015.
Кафедра №2, ВАС

5. Первый учебный вопрос

5
Первый учебный вопрос
Определение и свойства
частотных характеристик
ЛДС
Кафедра №2, ВАС

6. Первый учебный вопрос

6
Первый учебный вопрос
1. Определение частотных характеристик ЛДС
Воздействие – отрезок дискретного комплексного гармонического
сигнала
ˆ )e j ˆ n Ax (
ˆ )e j x ( ˆ ) , 0 n
x(n) Ax (
(1)
Кафедра №2, ВАС

7. Первый учебный вопрос

7
Первый учебный вопрос
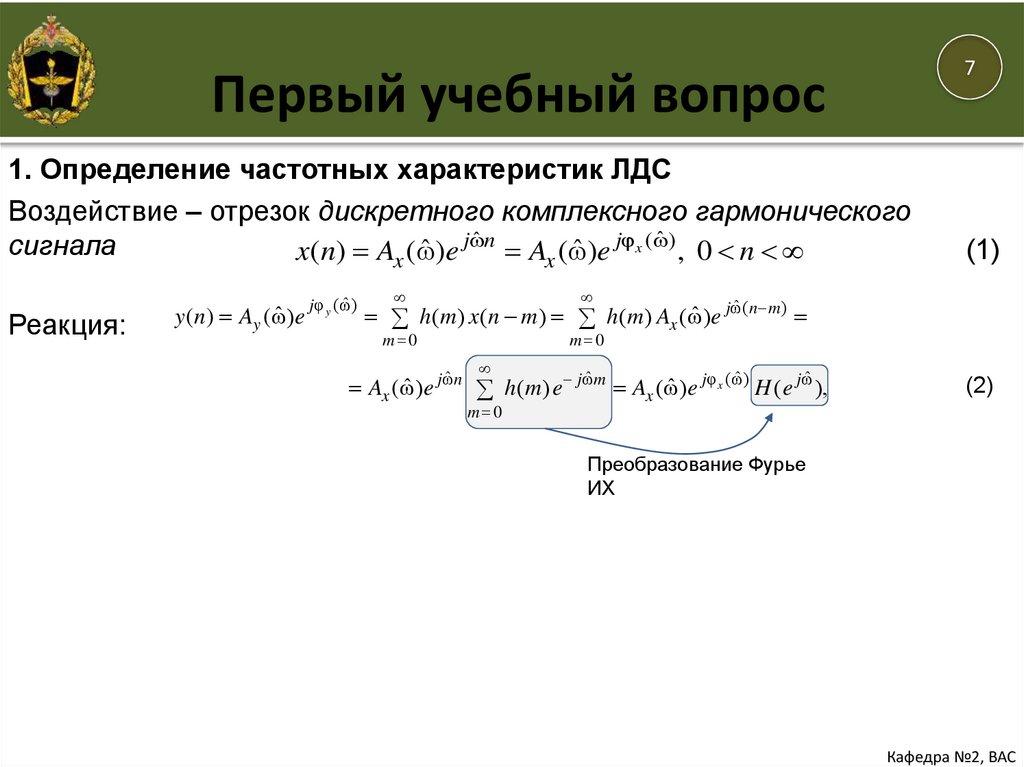
1. Определение частотных характеристик ЛДС
Воздействие – отрезок дискретного комплексного гармонического
сигнала
ˆ )e j ˆ n Ax (
ˆ )e j x ( ˆ ) , 0 n
x(n) Ax (
Реакция:
ˆ e
y ( n ) Ay (ω)
ˆ
jφ y (ω)
m 0
m 0
(1)
ˆ e jω̂( n m )
h( m) x ( n m ) h (m ) Ax (ω)
ˆ e
Ax (ω)
jωˆ n
ˆ
ˆ
ˆ e jφ x (ω)
H ( e jωˆ ),
h(m) e jωm Ax (ω)
(2)
m 0
Преобразование Фурье
ИХ
Кафедра №2, ВАС

8. Первый учебный вопрос

8
Первый учебный вопрос
1. Определение частотных характеристик ЛДС
Воздействие – отрезок дискретного комплексного гармонического
сигнала
ˆ )e j ˆ n Ax (
ˆ )e j x ( ˆ ) , 0 n
x(n) Ax (
Реакция:
ˆ e
y ( n ) Ay (ω)
ˆ
jφ y (ω)
m 0
m 0
ˆ e jω̂( n m )
h( m) x ( n m ) h (m ) Ax (ω)
ˆ e jωˆ n h( m) e jωˆ m Ax (ω)
ˆ e jφ x (ω) H ( e jωˆ ),
Ax (ω)
ˆ
m 0
ˆ )e
Ay (
jω̂
H (e )
(1)
ˆ)
j y (
ˆ )e
Ax (
ˆ e
Ay (ω)
ˆ
jφ y (ω)
ˆ e
Ax (ω)
ˆ
jφ x (ω)
Преобразование Фурье
ˆ)
ˆ
j ИХ
j
x (
ˆ
Ay (ω)
ˆ
Ax (ω)
H (e )
e
ˆ φ x (ω)
ˆ
j φ y (ω)
(2)
(3)
(4)
Кафедра №2, ВАС

9. Первый учебный вопрос

9
Первый учебный вопрос
1. Определение частотных характеристик ЛДС
Воздействие – отрезок дискретного комплексного гармонического
сигнала
ˆ )e j ˆ n Ax (
ˆ )e j x ( ˆ ) , 0 n
x(n) Ax (
Реакция:
ˆ e
y ( n ) Ay (ω)
ˆ
jφ y (ω)
m 0
m 0
ˆ e jω̂( n m )
h( m) x ( n m ) h (m ) Ax (ω)
ˆ e jωˆ n h( m) e jωˆ m Ax (ω)
ˆ e jφ x (ω) H ( e jωˆ ),
Ax (ω)
ˆ
m 0
ˆ )e
Ay (
jω̂
H (e )
(1)
ˆ)
j y (
ˆ e
Ay (ω)
ˆ )e
Ax (
ˆ
jφ y (ω)
ˆ
jφ x (ω)
Преобразование Фурье
ˆ)
ˆ
j ИХ
j
x (
ˆ
Ay (ω)
ˆ
Ax (ω)
H (e )
e
ˆ φ x (ω)
ˆ
j φ y (ω)
(2)
(3)
(4)
ˆ e
Ax (ω)
Определение 1:
Комплексной частотной характеристикой линейной дискретной системы называется
частотная зависимость отношения реакции к дискретному гармоническому воздействию
в установившемся режиме.
H ( z ) jω̂ H (e jω̂ )
(5)
z e
Кафедра №2, ВАС

10. Первый учебный вопрос

jωˆ
jωˆ
H (e ) H (e ) e
10
A(ω)
ˆ
ˆ e jφ(ω)
j arg H ( e jω̂ )
Кафедра №2, ВАС

11. Первый учебный вопрос

Аргумент
jωˆ
H (e ) H (e
jωˆ
) e
Модуль
jω̂
j arg H ( e )
ˆ e
A(ω)
ФЧХ
ˆ
j φ(ω)
11
(6)
АЧХ
Кафедра №2, ВАС

12. Первый учебный вопрос

Аргумент
jωˆ
H (e ) H (e
jωˆ
) e
jω̂
j arg H ( e )
ˆ e
A(ω)
ФЧХ
ˆ
j φ(ω)
12
(6)
АЧХ
Модуль
Определение 2:
Амплитудно-частотной характеристикой линейной дискретной системы
называется частотная зависимость отношения амплитуды реакции к
амплитуде дискретного гармонического воздействия в установившемся
(7)
режиме:
ˆ
A (ω)
ˆ
H (e jω̂ ) A(ω)
y
ˆ
Ax (ω)
.
Кафедра №2, ВАС

13. Первый учебный вопрос

Аргумент
jωˆ
H (e ) H (e
jωˆ
) e
jω̂
j arg H ( e )
ˆ e
A(ω)
ФЧХ
ˆ
j φ(ω)
13
(6)
АЧХ
Модуль
Определение 2:
Амплитудно-частотной характеристикой линейной дискретной системы
называется частотная зависимость отношения амплитуды реакции к
амплитуде дискретного гармонического воздействия в установившемся
(7)
режиме:
ˆ
Ay (ω)
ˆ
H (e jω̂ ) A(ω)
ˆ
Ax (ω)
.
Определение 3:
Фазочастотной характеристикой линейной дискретной системы называется
(8)
частотная зависимость разности начальных фаз реакции и дискретного
гармонического воздействия в установившемся режиме:
ˆ φ y (ω)
ˆ φ x (ω).
ˆ
φ(ω)
Кафедра №2, ВАС

14. Первый учебный вопрос

14
Связь частотной характеристики с передаточной функцией :
N 1
Частотная
характеристика
рекурсивной цепи
Частотная
характеристика
нерекурсивной цепи
ˆ
j
H ( z ) z e j ˆ H (e )
bi e j i
i 0
M 1
ˆ
1 bi e
ˆk
j
Y (e j ˆ )
X (e j ˆ )
(9)
k 1
ˆ
j
N 1
H ( z ) z e j ˆ H (e ) bi e
i 0
ˆi
j
Y (e j ˆ )
X (e j ˆ )
(9,а)
Кафедра №2, ВАС

15. Первый учебный вопрос

15
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
экспоненты e jωT и тригонометрических функций: sin, cos, tg и arctg.
Кафедра №2, ВАС

16. Первый учебный вопрос

16
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
экспоненты e jωT и тригонометрических функций: sin, cos, tg и arctg.
1. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочнонепрерывные) функции частоты по определению.
Кафедра №2, ВАС

17. Первый учебный вопрос

17
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
jω T
экспоненты e
и тригонометрических функций: sin, cos, tg и arctg.
1. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочнонепрерывные) функции частоты по определению.
2. Периодичность: ЧХ, АЧХ и ФЧХ — периодические функции частоты с
периодом, равным частоте дискретизации
2
д
(10)
T
Кафедра №2, ВАС

18. Первый учебный вопрос

18
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
jω T
экспоненты e
и тригонометрических функций: sin, cos, tg и arctg.
1. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочнонепрерывные) функции частоты по определению.
2. Периодичность: ЧХ, АЧХ и ФЧХ — периодические функции частоты с
периодом, равным частоте дискретизации
2
д
(10)
T
j ωT 2πk
e
e jωT e j 2πk
Кафедра №2, ВАС

19. Первый учебный вопрос

19
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
jω T
экспоненты e
и тригонометрических функций: sin, cos, tg и arctg.
1. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочнонепрерывные) функции частоты по определению.
2. Периодичность: ЧХ, АЧХ и ФЧХ — периодические функции частоты с
периодом, равным частоте дискретизации
2
д
(10)
T
e
j ωT 2πk
e jωT e j 2πk e jωT , k 0, 1, ...
=
1
Кафедра №2, ВАС

20. Первый учебный вопрос

20
2.Свойства частотных характеристик ЛДС
Свойства частотных характеристик определяются свойствами комплексной
jω T
экспоненты e
и тригонометрических функций: sin, cos, tg и arctg.
1. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочнонепрерывные) функции частоты по определению.
2. Периодичность: ЧХ, АЧХ и ФЧХ — периодические функции частоты с
периодом, равным частоте дискретизации
2
д
(10)
T
e
j ωT 2πk
e jωT e j 2πk e jωT , k 0, 1, ...
=
1
В зависимости от используемой шкалы частот период равен:
ˆ 2π.
f f д ; fˆ 1; ω ωд ; ω
Кафедра №2, ВАС

21. Первый учебный вопрос

21
3. Чётность и нечётность частотных характеристик (коэффициенты ПФ
вещественные):
Кафедра №2, ВАС

22. Первый учебный вопрос

22
3. Чётность и нечётность частотных характеристик (коэффициенты ПФ
вещественные):
АЧХ
H (e jωT ) H (e jωT )
- чётная функция частоты
Кафедра №2, ВАС

23. Первый учебный вопрос

23
3. Чётность и нечётность частотных характеристик (коэффициенты ПФ
вещественные):
H (e jωT ) H (e jωT )
АЧХ
ФЧХ
- чётная функция частоты
arg H (e jωT ) arg H (e jωT )
- нечётная функция частоты
Кафедра №2, ВАС

24. Второй учебный вопрос

24
Второй учебный вопрос
Вычисление частотных
характеристик ЛДС
Кафедра №2, ВАС

25. Второй учебный вопрос

25
1. Получить КЧХ
H ( z ) z e jω̂ H (e jω̂ )
(12)
Кафедра №2, ВАС

26. Второй учебный вопрос

1. Получить КЧХ
H ( z ) z e jω̂ H (e jω̂ )
26
N 1
(12)
H (e jω̂ )
ˆ
bi e j (iω)
i 0
M 1
(13)
ˆ
1 ak e j ( kω)
k 1
Кафедра №2, ВАС

27. Второй учебный вопрос

1. Получить КЧХ
H ( z ) z e jω̂ H (e jω̂ )
27
N 1
(12)
H (e jω̂ )
ˆ
bi e j (iω)
i 0
M 1
(13)
ˆ
1 ak e j ( kω)
k 1
jkωˆ
ˆ j sin(kω);
ˆ e jiωˆ cos(iω)
ˆ j sin(iω)
ˆ (14)
cos(kω)
2. Разложить экспоненты: e
Кафедра №2, ВАС

28. Второй учебный вопрос

1. Получить КЧХ
H ( z ) z e jω̂ H (e jω̂ )
28
N 1
(12)
H (e jω̂ )
ˆ
bi e j (iω)
i 0
M 1
(13)
ˆ
1 ak e j ( kω)
k 1
jkωˆ
ˆ j sin(kω);
ˆ e jiωˆ cos(iω)
ˆ j sin(iω)
ˆ (14)
cos(kω)
2. Разложить экспоненты: e
3. Выделить вещественные и мнимые части в числителе и знаменателе
КЧХ:
Re j Imч
H (e jω̂ ) ч
Reз j Imз
Кафедра №2, ВАС

29. Второй учебный вопрос

1. Получить КЧХ
29
N 1
H ( z ) z e jω̂ H (e jω̂ )
(12)
H (e jω̂ )
ˆ
bi e j (iω)
i 0
M 1
(13)
ˆ
1 ak e j ( kω)
k 1
jkωˆ
ˆ j sin(kω);
ˆ e jiωˆ cos(iω)
ˆ j sin(iω)
ˆ (14)
cos(kω)
2. Разложить экспоненты: e
3. Выделить вещественные и мнимые части в числителе и знаменателе
КЧХ:
N 1
N 1
ˆ j bi sin(iω)
ˆ
b0 bi cos(iω)
H (e jω̂ )
Re ч j Im ч
i 1
i 1
Re з j Im з M 1
M 1
ˆ j ak sin(kω)
ˆ
1 ak cos(kω)
k 1
k 1
(15)
Кафедра №2, ВАС

30. Второй учебный вопрос

30
Второй учебный вопрос
4. Записать АЧХ и ФЧХ согласно их определениям:
2
jω̂
ˆ H (e )
A(ω)
Reч 2 Im ч 2
Reз Im з
2
2
2
N 1
N 1
ˆ bi sin(iω)
ˆ
b0 bi cos(iω)
i 1
i 1
;
2
2
M 1
M 1
ˆ ak sin(kω)
ˆ
1 ak cos(kω)
k 1
k 1
(16)
Кафедра №2, ВАС

31. Второй учебный вопрос

31
Второй учебный вопрос
4. Записать АЧХ и ФЧХ согласно их определениям:
2
jω̂
ˆ H (e )
A(ω)
Reч 2 Im ч 2
Reз Im з
2
2
2
N 1
N 1
ˆ bi sin(iω)
ˆ
b0 bi cos(iω)
i 1
i 1
;
2
2
M 1
M 1
ˆ ak sin(kω)
ˆ
1 ak cos(kω)
k 1
k 1
(16)
Im
Im
ˆ arg H (e jω̂ ) arctg ч arctg з
φ(ω)
Reч
Reз
N 1
M 1
ˆ
bi sin(iω)
arctg
i 1
N 1
ˆ
b0 bi cos(iω)
i 1
M 1
ˆ
ak sin(kω)
arctg
k 1
M 1
ˆ
1 ak cos(kω)
k 1
ˆ
ak sin(kω)
arctg
k 1
M 1
ˆ
1 ak cos(kω)
k 1
(17)
N 1
bi sin(iωˆ )
arctg
i 1
N 1
.
ˆ
b0 bi cos(iω)
i 1
Кафедра №2, ВАС

32. Второй учебный вопрос

Пример 1.
H ( z)
32
b0 b1z 1
1 a1z 1
Кафедра №2, ВАС

33. Второй учебный вопрос

Пример 1.
H ( z)
b0 b1z 1
1 a1z 1
H (e jω̂ )
33
ˆ jb1 sin(ω)
ˆ
[b0 b1 cos(ω)]
ˆ ja1 sin(ω)
ˆ
[1 a1 cos(ω)]
Кафедра №2, ВАС

34. Второй учебный вопрос

Пример 1.
H ( z)
b0 b1z 1
1 a1z 1
ˆ 2 [b1 sin(ω)]
ˆ 2
[b0 b1 cos(ω)]
ˆ
A(ω)
ˆ 2 [a1 sin(ω)]
ˆ 2
[1 a1 cos(ω)]
H (e jω̂ )
34
ˆ jb1 sin(ω)
ˆ
[b0 b1 cos(ω)]
ˆ ja1 sin(ω)
ˆ
[1 a1 cos(ω)]
ˆ arctg
φ(ω)
ˆ
ˆ
a1 sin(ω)
b1 sin(ω)
arctg
ˆ
ˆ
1 a1 cos(ω)
b0 b1 cos(ω)
Кафедра №2, ВАС

35. Второй учебный вопрос

35
Второй учебный вопрос
Пример 1.
H ( z)
b0 b1z 1
H (e jω̂ )
1 a1z 1
ˆ 2 [b1 sin(ω)]
ˆ 2
[b0 b1 cos(ω)]
ˆ
A(ω)
ˆ 2 [a1 sin(ω)]
ˆ 2
[1 a1 cos(ω)]
Пример 2.
H ( z)
b0 b1z 1 b2 z 2
1 a1z 1 a2 z 2
H (e jω̂ )
ˆ jb1 sin(ω)
ˆ
[b0 b1 cos(ω)]
ˆ ja1 sin(ω)
ˆ
[1 a1 cos(ω)]
ˆ arctg
φ(ω)
ˆ
ˆ
a1 sin(ω)
b1 sin(ω)
arctg
ˆ
ˆ
1 a1 cos(ω)
b0 b1 cos(ω)
ˆ b2 cos(2ω)]
ˆ j b1 sin(ω)
ˆ b2 sin(2ω)
ˆ
[b0 b1 cos(ω)
ˆ a2 cos(2ω)]
ˆ j a1 sin(ω)
ˆ a2 sin(2ω)
ˆ
[1 a1 cos(ω)
ˆ b2 cos(2ω)]
ˆ 2 [b1 sin(ω)
ˆ b2 sin(2ω)]
ˆ 2
[b0 b1 cos(ω)
ˆ
A(ω)
ˆ a2 cos(2ω)]
ˆ 2 [a1 sin(ω)
ˆ a2 sin(2ω)]
ˆ 2
[1 a1 cos(ω)
ˆ arctg
φ(ω)
ˆ a2 sin(2ω)
ˆ
ˆ b2 sin(2ω)
ˆ
a1 sin(ω)
b1 sin(ω)
arctg
ˆ a2 cos(2ω)
ˆ
ˆ b2 cos(2ω)
ˆ
1 a1 cos(ω)
b0 b1 cos(ω)
Кафедра №2, ВАС

36. Третий учебный вопрос

36
Обобщающая схема связей
характеристик ЛДС
Кафедра №2, ВАС

37. Третий учебный вопрос

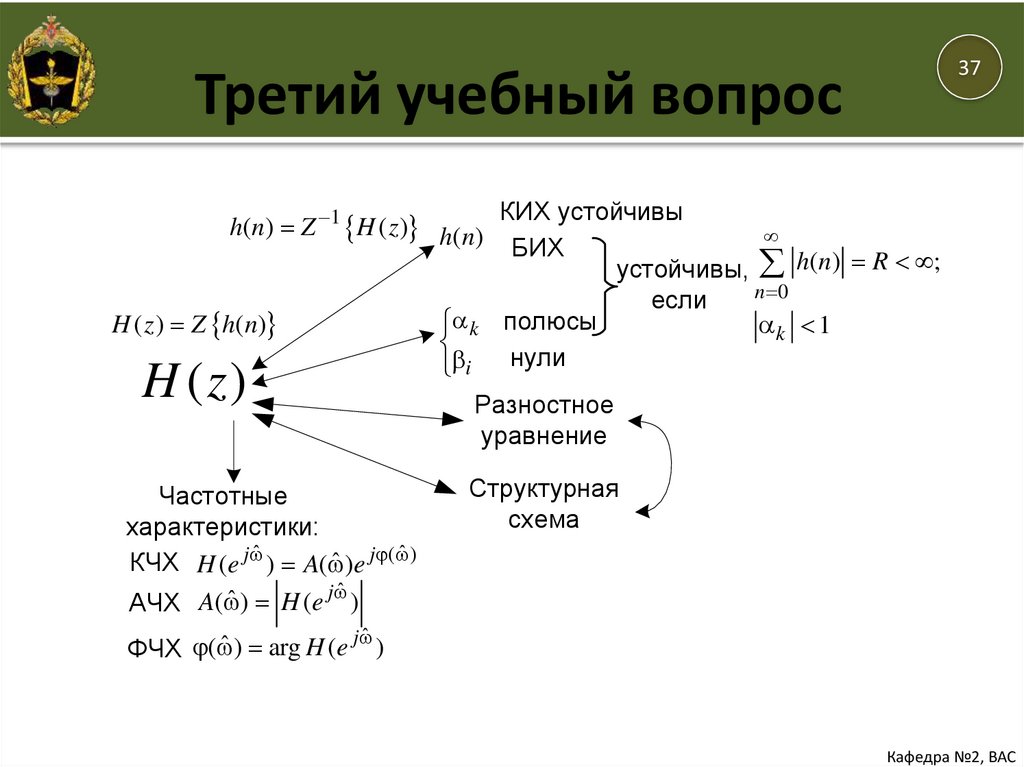
37
Третий учебный вопрос
h(n) Z 1 H ( z ) h(n)
H ( z ) Z h(n)
H ( z)
Частотные
характеристики:
ˆ )e j ( ˆ )
КЧХ H (e j ˆ ) A(
ˆ ) H (e j ˆ )
АЧХ A(
k
i
КИХ устойчивы
БИХ
устойчивы, h(n) R ;
n 0
если
полюсы
k 1
нули
Разностное
уравнение
Структурная
схема
ˆ ) arg H (e j ˆ )
ФЧХ (
Кафедра №2, ВАС

38.

ЛЕКЦИЯ ЗАВЕРШЕНА!