Similar presentations:
Расчёт частотных и импульсных характеристик БИХ-цепей 1-го порядка
1. Лекция по учебной дисциплине «Цифровая схемотехника и обработка сигналов» (Д-0205-1) Тема № 9: «Описание ЛДС в частотной
ВОЕННАЯ АКАДЕМИЯ СВЯЗИЛекция
по учебной дисциплине «Цифровая схемотехника и обработка
сигналов»
(Д-0205-1)
Тема № 9: «Описание ЛДС в частотной области»
Занятие № 30: «Расчёт частотных и импульсных
характеристик БИХ-цепей 1-го порядка»
Руководитель занятия – доцент кафедры, к.т.н., доцент,
полковник Филимонов Василий Александрович
г. Санкт-Петербург
2018
2. Учебные цели:
2Учебные цели:
Сформировать у курсантов навыки
самостоятельного расчёта и анализа
передаточных функций, частотных и
импульсных характеристик БИХ- цепей.
2.
Подготовить
курсантов
к
лабораторной работе
1.
Кафедра №2, ВАС
3. Учебные вопросы:
3Учебные вопросы:
1. Расчёт ИХ БИХ-цепей 1-го
порядка.
2. Расчёт
частотных
характеристик БИХ-цепей 1-го
порядка.
Кафедра №2, ВАС
4. Первый учебный вопрос
4Первый учебный вопрос
Расчёт ИХ БИХ-цепей 1-го
порядка
Кафедра №2, ВАС
5. Первый учебный вопрос
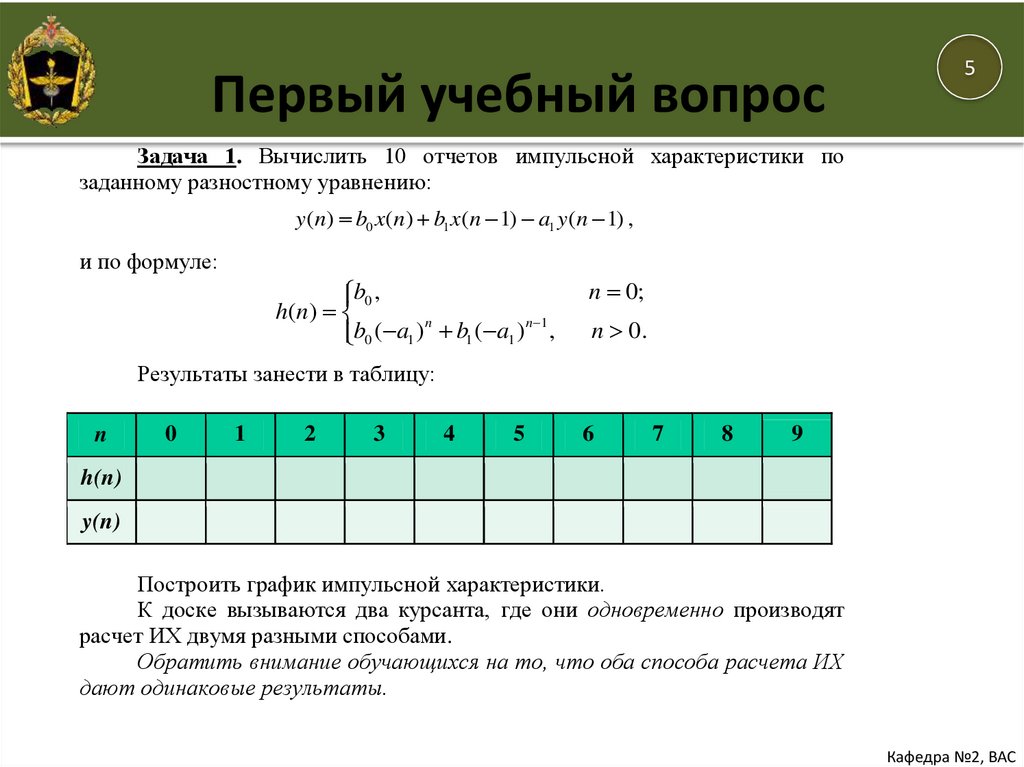
5Задача 1. Вычислить 10 отчетов импульсной характеристики по
заданному разностному уравнению:
y (n) b0 x(n) b1 x(n 1) a1 y (n 1) ,
и по формуле:
b0 ,
h( n)
n
n 1
b0 ( a1 ) b1 ( a1 ) ,
n 0;
n 0.
Результаты занести в таблицу:
n
0
1
2
3
4
5
6
7
8
9
h(n)
y(n)
Построить график импульсной характеристики.
К доске вызываются два курсанта, где они одновременно производят
расчет ИХ двумя разными способами.
Обратить внимание обучающихся на то, что оба способа расчета ИХ
дают одинаковые результаты.
Кафедра №2, ВАС
6. Второй учебный вопрос
6Второй учебный вопрос
Расчёт частотных
характеристик БИХ-цепей
1-го порядка
Кафедра №2, ВАС
7.
Второй учебный вопрос7
Задача 2. Получить выражения для АЧХ, ФЧХ и формулы экспрессанализа для вычисления АЧХ БИХ-цепи по заданному разностному
уравнению:
y (n) b0 x(n) b1 x(n 1) a1 y (n 1) .
Решение.
Y ( z ) b0 X ( z ) b1z 1 X ( z ) a1z 1Y ( z )
Y ( z ) 1 a1 z 1 X ( z ) b0 b1 z 1 .
Передаточная функция:
Y ( z ) b0 b1z 1
;
H ( z)
X ( z ) 1 a1z 1
Нуль z0 и полюс α z* передаточной функции (ПФ) вычисляются
по формулам:
b
z0 1 , z* a1
b0
Комплексная частотная характеристика в полной и показательной
формах записи:
Re1
H (e jω̂ ) H ( z )
z e jω̂
Im1
ˆ j b1 sin ω
ˆ
b0 b1e jω̂ b0 b1 cos ω
ˆ j a1 sin ω
ˆ
1 a1e jω̂
1 a1 cos ω
Re 2
H (e jω̂ ) e jargH ( e
jω̂
)
ˆ e
A(ω)
Im 2
ˆ
jφ ω
Кафедра №2, ВАС
8.
Второй учебный вопрос8
получается после подстановки в передаточную функцию:
ˆ
z e jωˆ ; z 1 e jωˆ cosωˆ j sin ω;
ˆ j sin ω
ˆ cos 2 ω
ˆ sin 2 ω
ˆ 1.
z 1 e jωˆ cosω
Обратить внимание на то, что при изменении частот от 0 до 2π
описывается окружность (как в тригонометрии!).
Для удобства сравнения частотных характеристик различных
цифровых цепей и задания требований к этим характеристикам обычно
частоту и АЧХ нормируют. Нормированные характеристики отмечаются
знаком , например fˆ , ̂ и т. д.
Нормированной частотой fˆ называется отношение текущей частоты f
к частоте дискретизации f д :
f
fˆ
fT .
fд
Тогда интервал частот f [0; f д / 2] преобразуется в интервал частот
fˆ [0; 0,5] .
Кафедра №2, ВАС
9.
Второй учебный вопрос9
Нормированная круговая частота определяется соотношением
ˆ
f
2
2 fˆ 2 fT T [рад].
fд
fд
Частотам fˆ , расположенным в интервале [0; 0,5] , соответствуют
частоты ̂ из интервала [0; ] .
Амплитудно-частотная характеристика:
ˆ
A(ω)
Re12 Im12
Re22 Im 22
b0 b1 cosωˆ b1 sin ωˆ
2
2
1 a1 cos ωˆ a1 sin ωˆ
2
2
;
при этом обычно используется нормированная АЧХ:
ˆ
Aˆ (ω)
ˆ
A(ω)
1.
ˆ
max A(ω)
ω̂
Фазочастотная характеристика определяется как разность аргументов
числителя
ˆ
ˆ
b1 sin ω
b1 sin ω
ˆ arctg
arg числителя φ1 (ω)
arctg
ˆ
ˆ
b0 b1 cosω
b0 b1 cosω
и знаменателя
ˆ
a sin ω
ˆ arctg 1
arg знаменателя φ2 (ω)
:
ˆ
1 a1 cosω
ˆ
ˆ
b1 sin ω
a sin ω
ˆ arg H (e jω̂ φ1 (ω)
ˆ φ 2 (ω)
ˆ arctg
φ(ω)
arctg 1
.
ˆ
ˆ
b
b
cos
ω
1
a
cos
ω
0
1
1
Кафедра №2, ВАС
10.
Второй учебный вопрос10
Формулы экспресс-анализа для цепей 1-го порядка записывают при
ˆ π 2 :
ˆ π,ω
ˆ 0,ω
ω
1. ω̂ 0 ;
b b
b b
H (e jω̂ ) ω̂ 0 H (1) 0 1 ; A(0) 0 1 ;
1 a1
1 a1
2. ω̂ π ;
b b
b b
H (e jω̂ ) ω̂ π H ( 1) 0 1 ; A(0) 0 1 ;
1 a1
1 a1
3. ω̂ π 2 ;
H (e
jπ 2
b jb1 sin ωˆ
) H ( j) 0
1 ja1 sin ωˆ
ω̂
π
2
b02 b12
b0 jb1
π
.
; A
1 a12
1 ja1
2
Кафедра №2, ВАС
11.
Второй учебный вопрос11
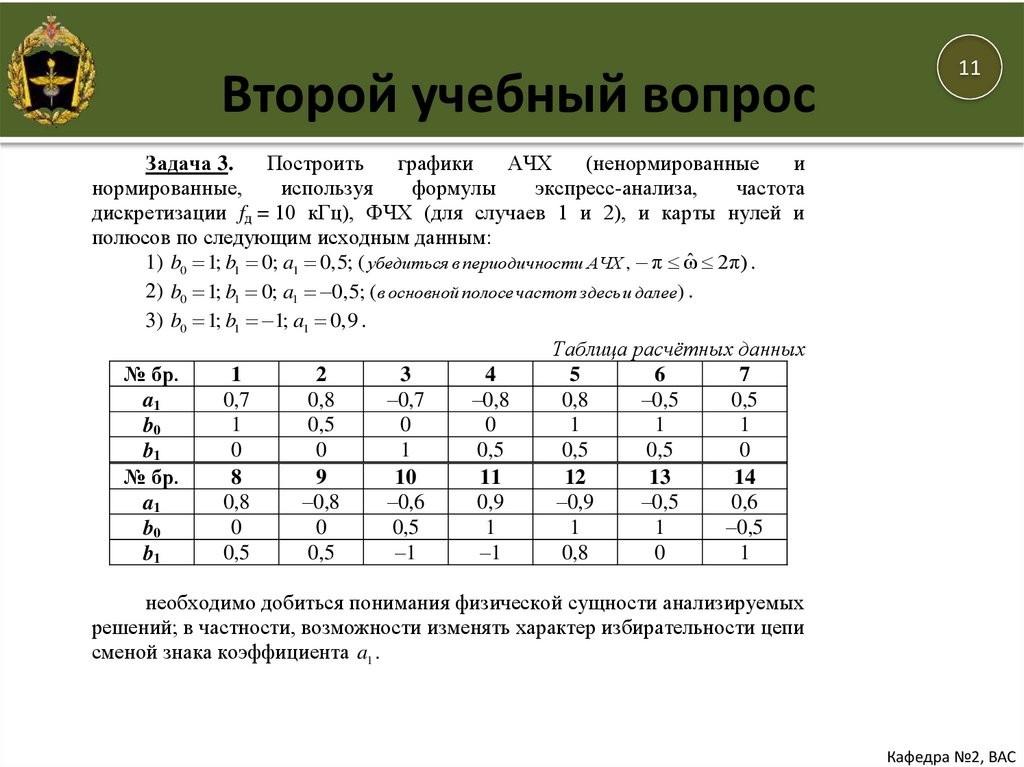
Задача 3.
Построить
графики
АЧХ
(ненормированные
и
нормированные,
используя
формулы
экспресс-анализа,
частота
дискретизации fд = 10 кГц), ФЧХ (для случаев 1 и 2), и карты нулей и
полюсов по следующим исходным данным:
ˆ 2π) .
1) b0 1; b1 0; a1 0,5; ( убедиться в периодичности АЧХ , π ω
2) b0 1; b1 0; a1 0,5; (в основной полосечастот здесьи далее) .
3) b0 1; b1 1; a1 0,9 .
Таблица расчётных данных
№ бр.
1
2
3
4
5
6
7
0,7
0,8
–0,7
–0,8
0,8
–0,5
0,5
a1
1
0,5
0
0
1
1
1
b0
0
0
1
0,5
0,5
0,5
0
b1
№ бр.
8
9
10
11
12
13
14
0,8
–0,8
–0,6
0,9
–0,9
–0,5
0,6
a1
0
0
0,5
1
1
1
–0,5
b0
0,5
0,5
–1
–1
0,8
0
1
b1
необходимо добиться понимания физической сущности анализируемых
решений; в частности, возможности изменять характер избирательности цепи
сменой знака коэффициента a1 .
Кафедра №2, ВАС
12.
Второй учебный вопрос12
Анализ полученных решений:
частотные характеристики являются периодическими функциями
частоты;
нули и полюсы цепей первого порядка являются вещественными;
изменение знака коэффициента a1 приводит к инверсии АЧХ;
увеличение коэффициента a1 по модулю приводит к более высокой
избирательности АЧХ;
АЧХ цифровой цепи может превышать 1, т. е. цифровые цепи обладают
свойством усиления;
ˆ 0 на частоте ω̂ 0 , если b0 b1 , и на
при b0 b1 получаем A(ω)
частоте ω̂ π , если b0 b1 ;
импульсная характеристика при a1 0 является знакопостоянной
(случай НЧ-фильтра), а при a1 0 – знакопеременной (случай ВЧ-фильтра).
Кафедра №2, ВАС










 mathematics
mathematics








