Автоматика и управление. Тема 4. Частотные характеристики ЛСС. Лекция 4. Реакция ЛСС на гармонический входной сигнал

1.

Автоматика и управление
Тема 4. Частотные
характеристики ЛСС
Лекция 4. Реакция ЛСС на гармонический входной сигнал, заданный в
комплексном виде. Определение амплитудно-фазовой частотной
характеристики (АФЧХ). Годограф АФЧХ. Вещественная, мнимая,
амплитудная (АЧХ) и фазовая (ФЧХ) частотные характеристики.
Логарифмические
частотные
характеристики
(ЛЧХ). Частотные
характеристики элементарных динамических звеньев. Частотные
характеристики соединений звеньев.

2.

4.1. Реакция ЛСС на гармонический входной сигнал,
заданный в комплексном виде
Как будет реагировать система на гармонический входной сигнал
различной частоты?
Как зависят динамические свойства системы от частоты гармонического
входного сигнала?
Такая зависимость выражается частотными характеристиками (ЧХ)
Частотные характеристики - это динамические
характеристики, являющиеся функциями частоты
гармонического входного сигнала и определяющие
реакцию системы на этот сигнал.

3.

Рассмотрим одномерную ЛСС с одним входом
any(n)(t)+an-1y(n-1)(t)+...+a1y(1)(t)+a0y(t)= вmx(m)(t)+ вm-1x(m-1)(t) +...
+в1x(1)(t)+в0x(t)
Передаточная функция
B( p) вm p m в1 p в0
B( p)
Ф( p )
n
an ( p p1 )( p p2 ) ( p pn )
A( p) an p a1 p a0
где pi - полюса передаточной функции Ф(p), i = 1, n
Подадим на вход гармонический входной сигнал
где Ax - амплитуда входного сигнала,
x(t) = Ax Sin(ω t + x)
- частота входного сигнала,
x - фаза входного сигнала.
В комплексном виде:
x( t ) Ax e
A x Ax e j
x
j ( t x )
Ax e e
j t
j x
j t
Ax e
t = t0 = 0
A x Ax
arg A x x
- комплексная амплитуда входного сигнала

4.

:
Найдем изображение по Лапласу входного сигнала X(p):
X(p) = L[x(t)] = L[ A x e j t ] = A x L[e j t ]
L [ e t ]
Пусть j = , тогда
1
p
A x
X(p) = L[x(t)] =
p j
Y(p) = X(p)Ф(p)
A x
B ( p ) / an
Y ( p)
( p j ) ( p p1 )( p p2 ) ( p pn )
Допустим, корни характеристического уравнения A(p)=O
простые, некратные и Re[pi] < 0 Тогда по теореме разложения
~
~
n
C0
Ci
Y ( p ) Ax
p
j
p
p
i 1
i

5.

~
Определим коэффициент C0
~
C0
B( p)
B ( j )
B ( j )
Ф ( j )
(1)
(1)
[( p j ) A( p)] p j A( j ) ( j j ) A ( j ) A( j )
Применив операцию обратного преобразования Лапласа,
получим оригинал выходного сигнала ЛСС, находящейся под
воздействием гармонического входного сигнала:
y(t) = A x [ Ф(j )e
j t
~ pit
Ci e ] y в ( t ) y c ( t )
i 1
вынужденная гармоническая составляющая
выходного сигнала ЛСС, имеющая частоту
входного сигнала
если Re [pi] < 0
n
свободная составляющая выходного
сигнала ЛСС, которая существует в
переходный период
A C~ e p t 0
lim x i
n
yc(t)=
i
t
i 1
y(t) ≈ yв (t)

6.

4.2. Определение амплитудно-фазовой частотной
характеристики (АФЧХ)
Найдем отношение вынужденной составляющей выходного
сигнала ЛСС к гармоническому входному сигналу
yв ( t ) A xФ(j )e j t
Ф(j ) Ф(р)
j t
x( t )
Ax e
p j
Амплитудно-фазовой частотной характеристикой Ф(j )
(АФЧХ) ЛСС или комплексным коэффициентом усиления
называется отношение вынужденной составляющей
выходного сигнала к гармоническому входному сигналу,
представленным в комплексной форме.

7.

Получают АФЧХ ЛСС Ф(j ) путем замены в передаточной
функции системы комплексной переменной p на мнимую
переменную j :
Ф(j )
в m (j )m в m-1 (j )m 1 в0
a n (j )n a n 1 (j )n 1 a0
АФЧХ, являясь функцией частоты входного сигнала , зависит
от параметров ai , вi системы.

8.

4.3. Вещественная, мнимая, амплитудная и фазовая
частотные характеристики
Ф(j ) = Фa( )ej ( )= R( ) + jI(ω)
Фa( ) = Ф(j )
yв ( t )
x( t )
Ay ( )
Ax
( ) = argФ(j )
y ( ) x
Функция Фa( ) = |Ф(j )| называется амплитудночастотной характеристикой (АЧХ) ЛСС или
коэффициентом усиления по амплитуде гармонического
сигнала.
Функция ( ) = аrg Ф(j ) называется фазовой частотной
характеристикой (ФЧХ) ЛСС.

9.

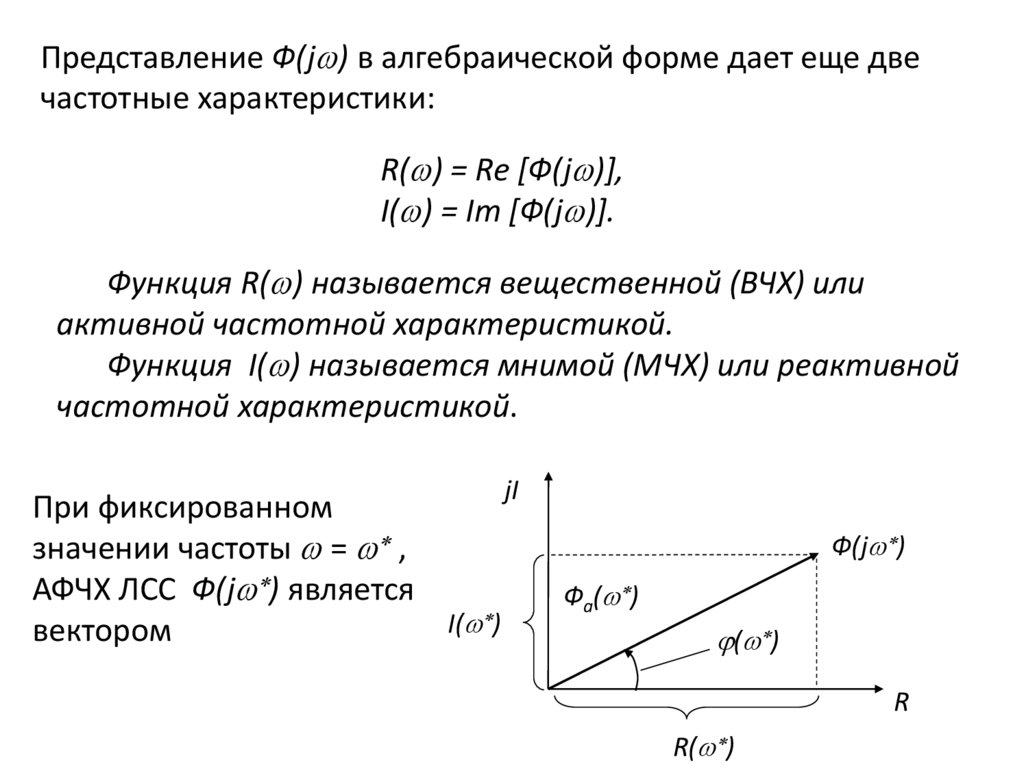
Представление Ф(j ) в алгебраической форме дает еще две
частотные характеристики:
R( ) = Re [Ф(j )],
I( ) = Im [Ф(j )].
Функция R( ) называется вещественной (ВЧХ) или
активной частотной характеристикой.
Функция I( ) называется мнимой (МЧХ) или реактивной
частотной характеристикой.
При фиксированном
значении частоты = ,
АФЧХ ЛСС Ф(j ) является
I( )
вектором
jI
Ф(j )
Фа( )
( )
R
R( )

10.

Фа ( ) R 2 ( ) I 2 ( ),
R( ) Фa ( ) cos ( )
I( )
( ) arctg
,
R( )
I ( ) Фa ( ) sin ( )
Фа ( ) Ф(j )
Bj )
Aj )
R B2 ( ) I B2 ( )
R A2 ( ) I A2 ( )
.
I в ( )
I А ( )
( ) = argФ(j ) = argB(j )-argA(j ) = arctg
- arctg R ( )
R в ( )
А
RB( ) = в0 –в2 2+в4 4 +...- вещественная часть B(j ),
IB( ) = в1 –в3 3+в5 5 +...- мнимая часть B(j ),
RA( ) = a0 –a2 2+a4 4 +...- вещественная часть A(j ),
IA( ) = a1 –a3 3+a5 5 +...- мнимая часть A(j )

11.

yв(t) ≈ y(t) = A x Ф(j )еj t= Ax еj( t+ x) Ф(j )
Ф( j ) Ф ( )е j ( )
y(t) = Ax еj( t+ x) Фa( ) еj ( ) = AxФa( )еj[ t+ x+ ( ])
Ay= Ax Фa( ) x
y= ( )
x + x
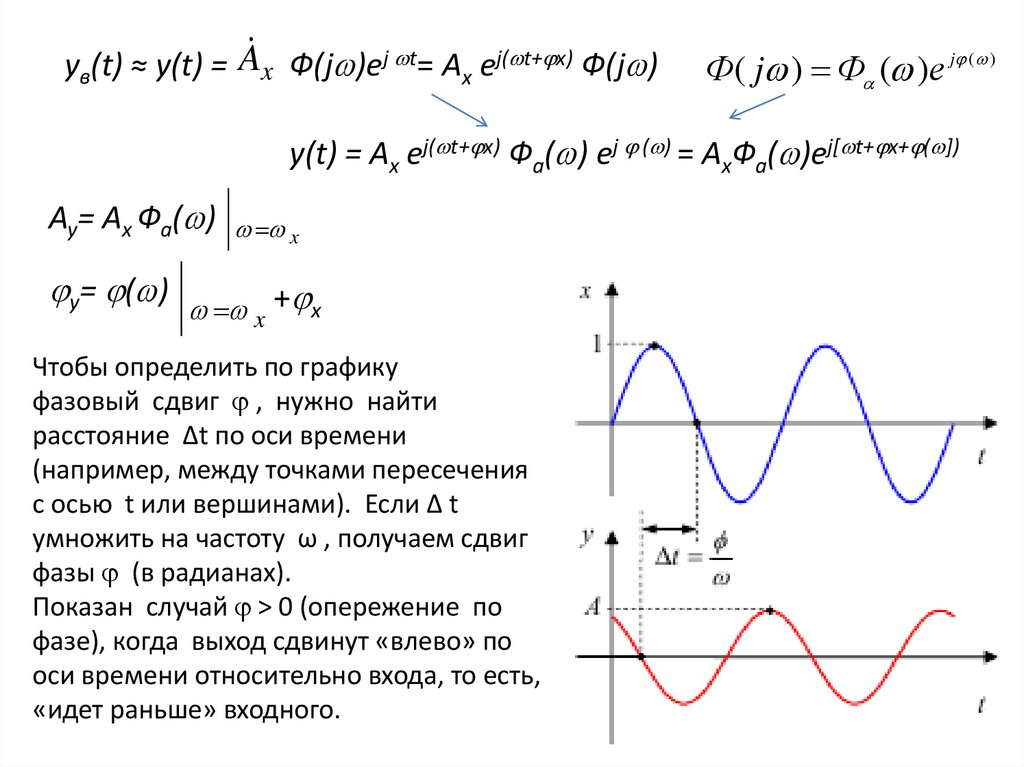
Чтобы определить по графику
фазовый сдвиг , нужно найти
расстояние ∆t по оси времени
(например, между точками пересечения
с осью t или вершинами). Если ∆ t
умножить на частоту ω , получаем сдвиг
фазы (в радианах).
Показан случай > 0 (опережение по
фазе), когда выход сдвинут «влево» по
оси времени относительно входа, то есть,
«идет раньше» входного.

12.

1. Реакция ЛСС в установившемся режиме на гармонический
входной сигнал x(t)=Ax Sin( x t+ x) с частотой x, есть
также гармонический сигнал с той же частотой x:
y(t)=AySin( x t+ y).
2. Амплитуда выходного сигнала Ay зависит от амплитуды
входного сигнала Ax, его частоты x и параметров ai , вi
(собственных свойств) системы.
3. Фаза выходного сигнала y зависит от фазы входного
сигнала x, его частоты x и параметров ai, вi системы.
Выражения также справедливы для вычисления ошибки АС в
установившемся режиме. В этом случае необходимо
оперировать с ЧХ АС от соответствующего входного сигнала к
ошибке.

13.

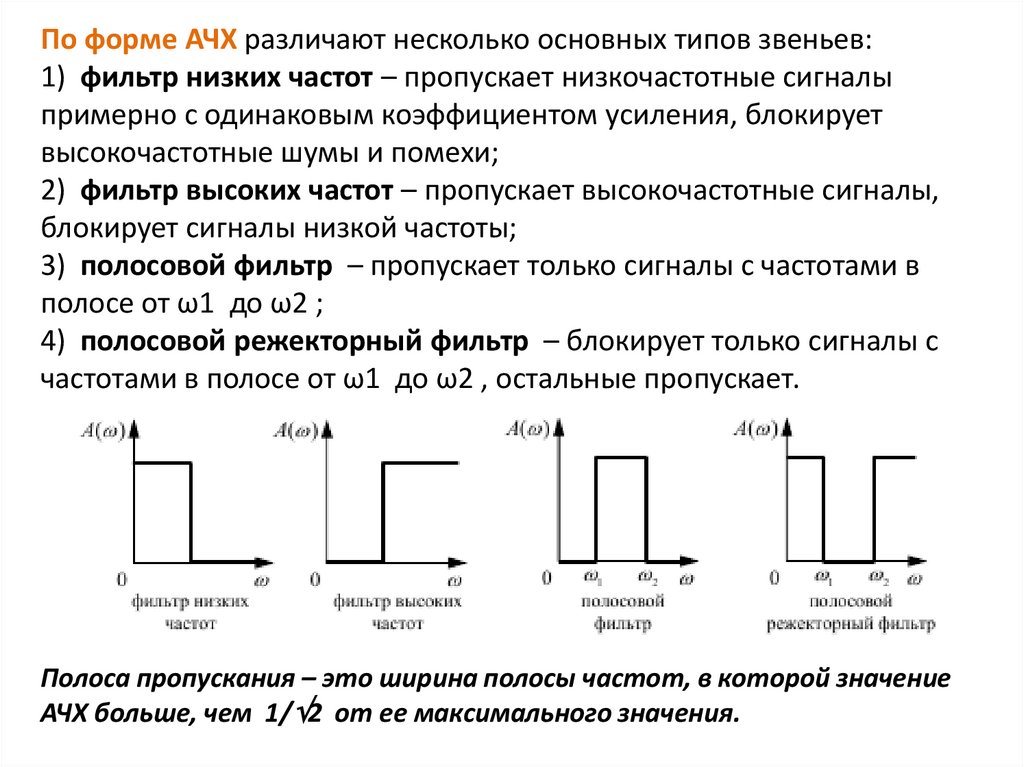
По форме АЧХ различают несколько основных типов звеньев:
1) фильтр низких частот – пропускает низкочастотные сигналы
примерно с одинаковым коэффициентом усиления, блокирует
высокочастотные шумы и помехи;
2) фильтр высоких частот – пропускает высокочастотные сигналы,
блокирует сигналы низкой частоты;
3) полосовой фильтр – пропускает только сигналы с частотами в
полосе от ω1 до ω2 ;
4) полосовой режекторный фильтр – блокирует только сигналы с
частотами в полосе от ω1 до ω2 , остальные пропускает.
Полоса пропускания – это ширина полосы частот, в которой значение
АЧХ больше, чем 1/ 2 от ее максимального значения.

14.

Годограф АФЧХ
Если изменять частоту входного сигнала от 0 до , то точка,
отображающая конец радиус-вектора АФЧХ Ф(j ), опишет
некоторую траекторию на комплексной плоскости
Траектория точки, отображающей АФЧХ
Ф(j ) на
комплексной плоскости при изменении частоты от 0 до ,
называется годографом АФЧХ системы.
Один из точных методов
построения годографа АФЧХ
ЛСС - по параметрам
скалярных частотных
характеристик: R( ), I( ), или
Фa( ) и ( ) в декартовых или
полярных координатах,
соответственно.
jI
=
1< 2< 3
Ф(j 3)
3
Ф(j 2)
Ф(j0)
2
1
=0
Ф(j 1)
R

15.

Логарифмические частотные характеристики ЛСС
Для наглядного графического изображения частотных
характеристик в широком диапазоне частот, используют
логарифмические частотные характеристики (ЛЧХ).
Логарифмические частотные характеристики – это
совокупность двух графиков:
1. Логарифмическая амплитудно-частотная
характеристика (ЛАХ)
L( ) - это характеристика, вычисленная по формуле
L( ) = 20lgWа( )
и построенная в функции логарифма частоты
2. Логарифмическая фазо - частотная характеристика
(ЛФХ) - это график фазо - частотной характеристики ( ),
построенной в функции логарифма частоты .

16.

При построении графиков ЛЧХ, за единицу логарифмического
масштаба по оси частот (абсцисс) принята декада.
Декада - это отрезок оси частот, на котором частота
изменяется в 10 раз.
10
1 декада = lg10 - lg = lg
= lg10 = 1
Декада не зависит от выбора частоты отсчета и
графически изображается отрезком постоянной длины:
1 декада
0,1
1 декада
1
10
100
,с-1

17.

Так как, при =0 lg =lg0=- , то за начало отсчета может быть
принята любая частота 0 0.
Как правило, 0 выбирается с учетом рабочего диапазона
частот данной АС.
Тогда расстояние l от выбранного начала координат 0 до
точки с частотой будет
0
l
l=lg -lg 0=lg
0
При построении ЛАХ по оси ординат вместо коэффициента
усиления по амплитуде Wа(ω) откладывается величина
L( )=20lgWa( ). Единицей масштаба по этой оси является
децибел.
Один децибел соответствует такому коэффициенту
усиления АС по амплитуде К0=Аy /Аx , что 20lgК0 =1, т.е.
К0 =100,05=1,21

18.

При построении ЛФХ по оси ординат, точно так же как и при построении
ФЧХ АС ( ), фазовый сдвиг откладывается в обычных единицах, т.е. в
градусах или радианах.
Зависимость коэффициента усиления АС по амплитуде,
выраженного в децибелах [L( )], от логарифма частоты
lg / 0 , называется логарифмической амплитудной
характеристикой (ЛАХ);
Зависимость фазового сдвига АС ( ), выраженного в
градусах или радианах, от логарифма частоты lg / 0,
называется логарифмической фазовой характеристикой
(ЛФХ).
Вместе ЛАЧХ и ЛФЧХ называются логарифмической
амплитудно-фазовой частотной характеристикой
(ЛАФЧХ) или диаграммой Боде.
Частота , при которой ЛАХ пересекает ось абсцисс, то есть
L( с)=0, a Wa( с )=1, называется частотой среза.

19.

Логарифмические характеристики обладают двумя ценными
свойствами:
1) ЛАЧХ и ЛФЧХ для произведения W1(p) W2(p) вычисляются
как суммы ЛАЧХ и ЛФЧХ отдельных звеньев:
20 lgWa ( ) 20 lgWa1 ( ) 20 lgWa 2 ( )
( ) 1 ( ) 2 ( )
2) в области высоких и низких частот ЛАЧХ асимптотически
приближаются к прямым, наклон которых составляет ±20
дБ/дек (децибел на декаду), ±40 дБ/дек и т.д.

20.

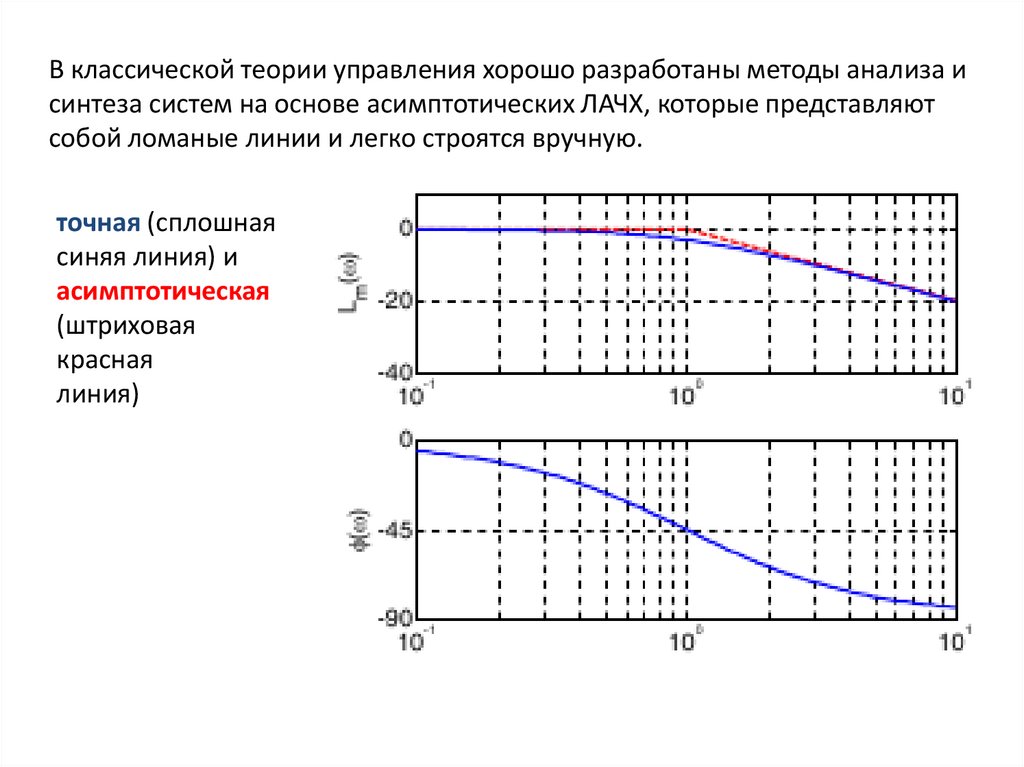
В классической теории управления хорошо разработаны методы анализа и
синтеза систем на основе асимптотических ЛАЧХ, которые представляют
собой ломаные линии и легко строятся вручную.
точная (сплошная
синяя линия) и
асимптотическая
(штриховая
красная
линия)

21.

Частотные характеристики элементарных динамических
звеньев
Усилительное звено a0 y(t)=в0 x(t) или y(t)=K x(t)
W(p)=K
Если на вход усилителя действует синусоидальный сигнал, на
выходе он усиливается в k раз без изменения фазы, поэтому
амплитудная и фазовая частотная характеристики не зависят от
частоты входного сигнала:
в0
K
a0
Wa(ω) =k , (ω) =0
,град
jI
L, дб
L( ),K>1
W(j )
L( ),K=1
180
40
90
20
20lgK
( )
L( ),K<1
0 0
0
R
АФЧХ
1
10
100
ЛАЧХ и ЛФЧХ
, c-1

22.

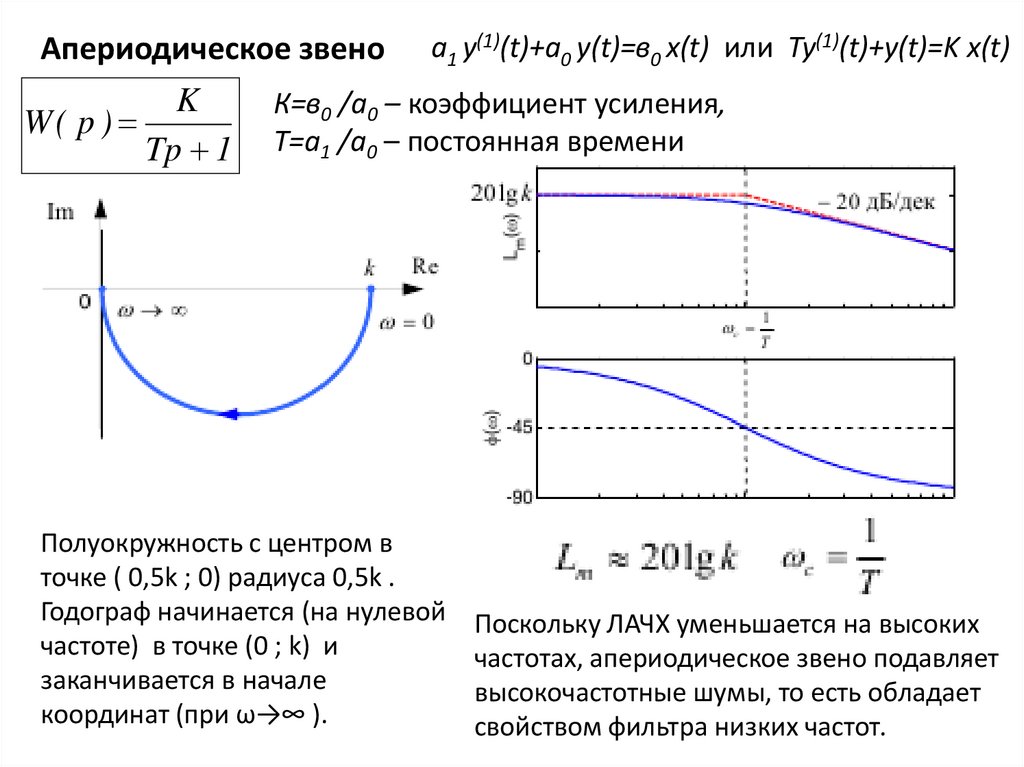
Апериодическое звено
K
W( p )
Tp 1
a1 y(1)(t)+a0 y(t)=в0 x(t) или Ty(1)(t)+y(t)=K x(t)
К=в0 /а0 – коэффициент усиления,
Т=а1 /а0 – постоянная времени
Полуокружность с центром в
точке ( 0,5k ; 0) радиуса 0,5k .
Годограф начинается (на нулевой
частоте) в точке (0 ; k) и
заканчивается в начале
координат (при ω→∞ ).
Поскольку ЛАЧХ уменьшается на высоких
частотах, апериодическое звено подавляет
высокочастотные шумы, то есть обладает
свойством фильтра низких частот.

23.

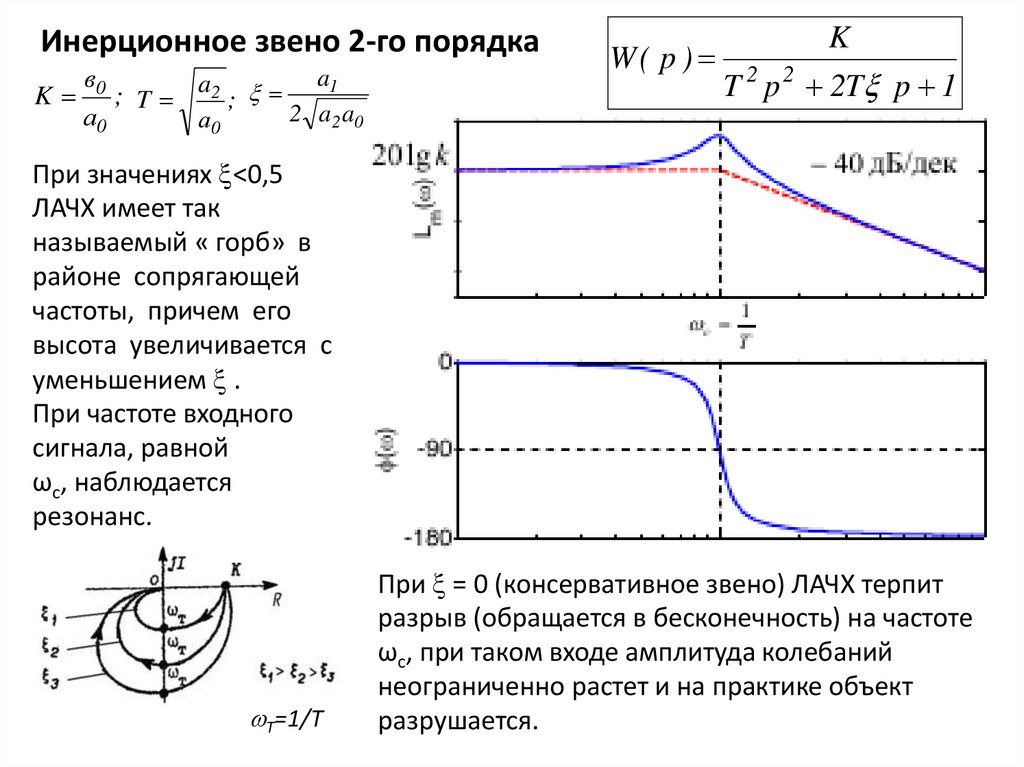
Инерционное звено 2-го порядка
a1
в
K 0 ; T a2 ;
2 a2 a0
а0
а0
W( p )
K
T 2 p 2 2T p 1
При значениях <0,5
ЛАЧХ имеет так
называемый « горб» в
районе сопрягающей
частоты, причем его
высота увеличивается с
уменьшением .
При частоте входного
сигнала, равной
ωc, наблюдается
резонанс.
T=1/Т
При = 0 (консервативное звено) ЛАЧХ терпит
разрыв (обращается в бесконечность) на частоте
ωc, при таком входе амплитуда колебаний
неограниченно растет и на практике объект
разрушается.

24.

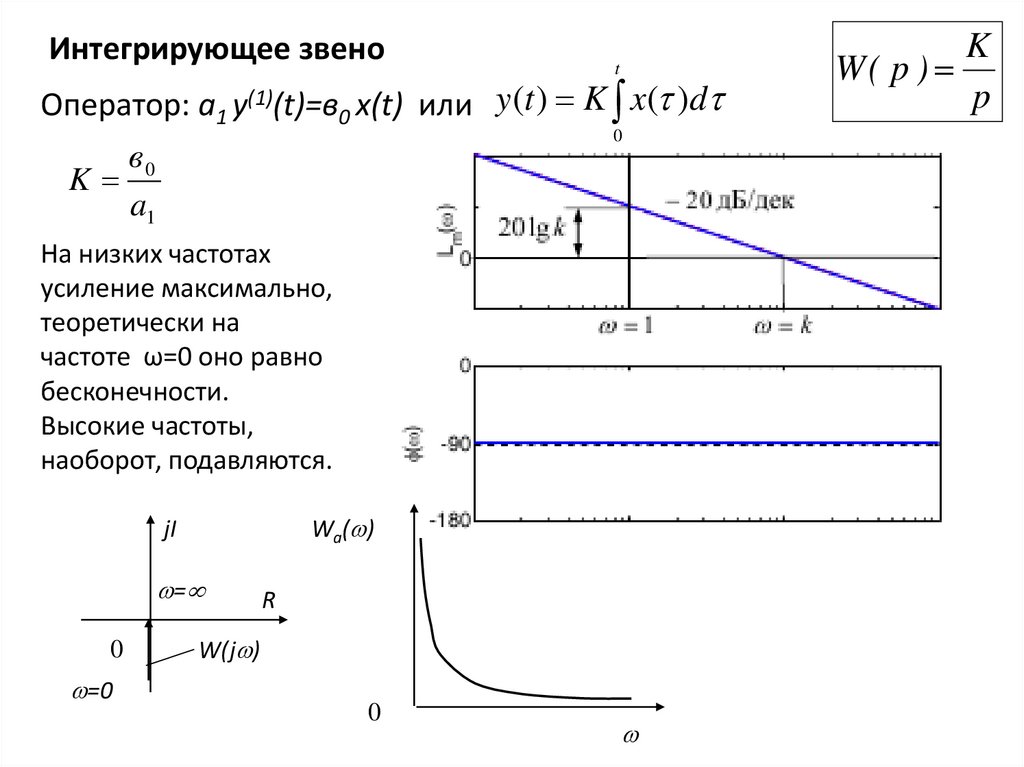
Интегрирующее звено
t
Оператор: a1 y(1)(t)=в0 x(t) или y (t ) K x( )d
0
в0
K
a1
На низких частотах
усиление максимально,
теоретически на
частоте ω=0 оно равно
бесконечности.
Высокие частоты,
наоборот, подавляются.
Wa( )
jI
=
0
=0
R
W(j )
0
K
W( p )
p

25.

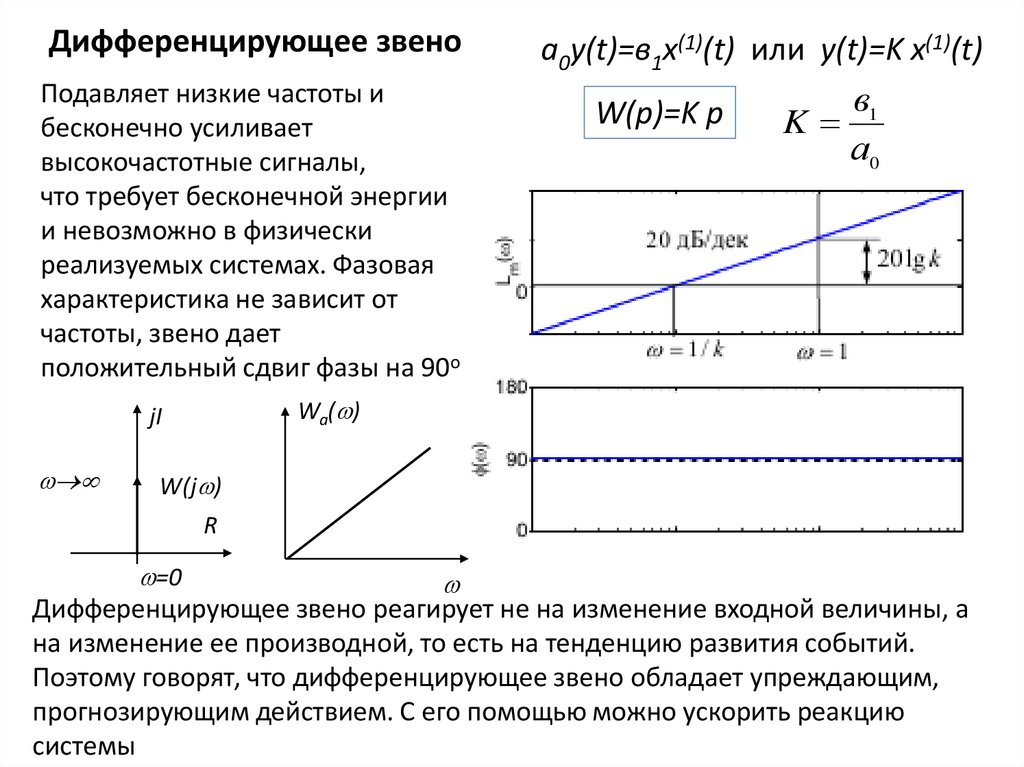
Дифференцирующее звено
Подавляет низкие частоты и
бесконечно усиливает
высокочастотные сигналы,
что требует бесконечной энергии
и невозможно в физически
реализуемых системах. Фазовая
характеристика не зависит от
частоты, звено дает
положительный сдвиг фазы на 90o
W(p)=K p
в1
K
а0
Wa( )
jI
a0y(t)=в1х(1)(t) или y(t)=K x(1)(t)
W(j )
R
=0
Дифференцирующее звено реагирует не на изменение входной величины, а
на изменение ее производной, то есть на тенденцию развития событий.
Поэтому говорят, что дифференцирующее звено обладает упреждающим,
прогнозирующим действием. С его помощью можно ускорить реакцию
системы

26.

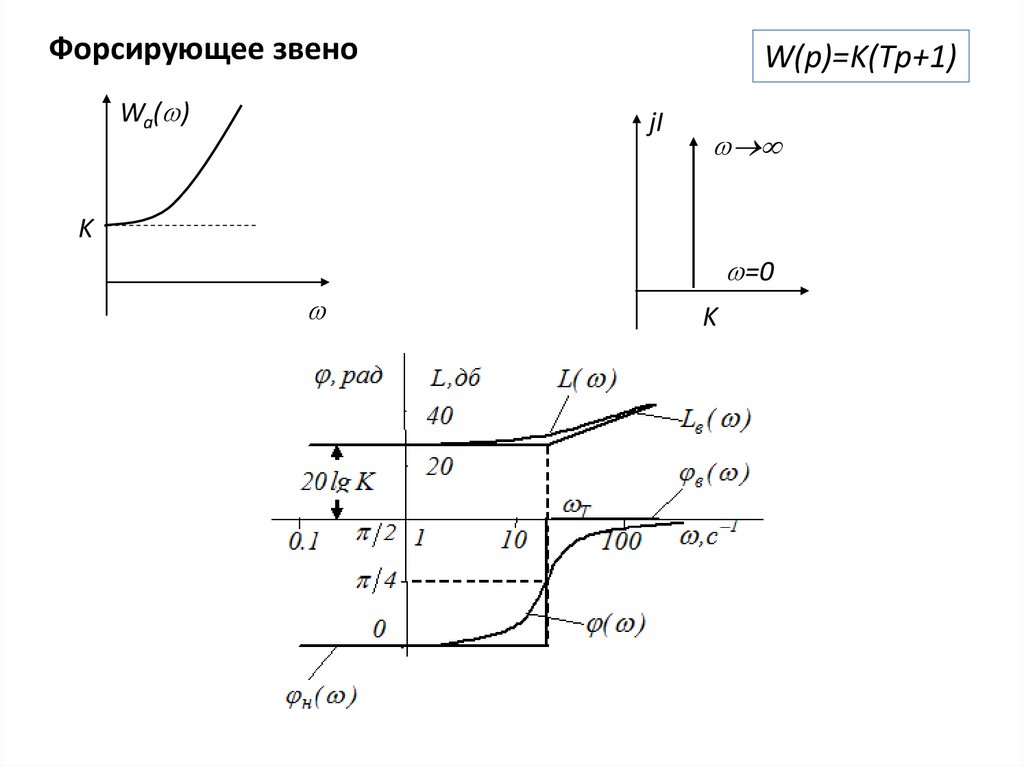
Форсирующее звено
Wa( )
W(p)=K(Тp+1)
jI
K
=0
K

27.

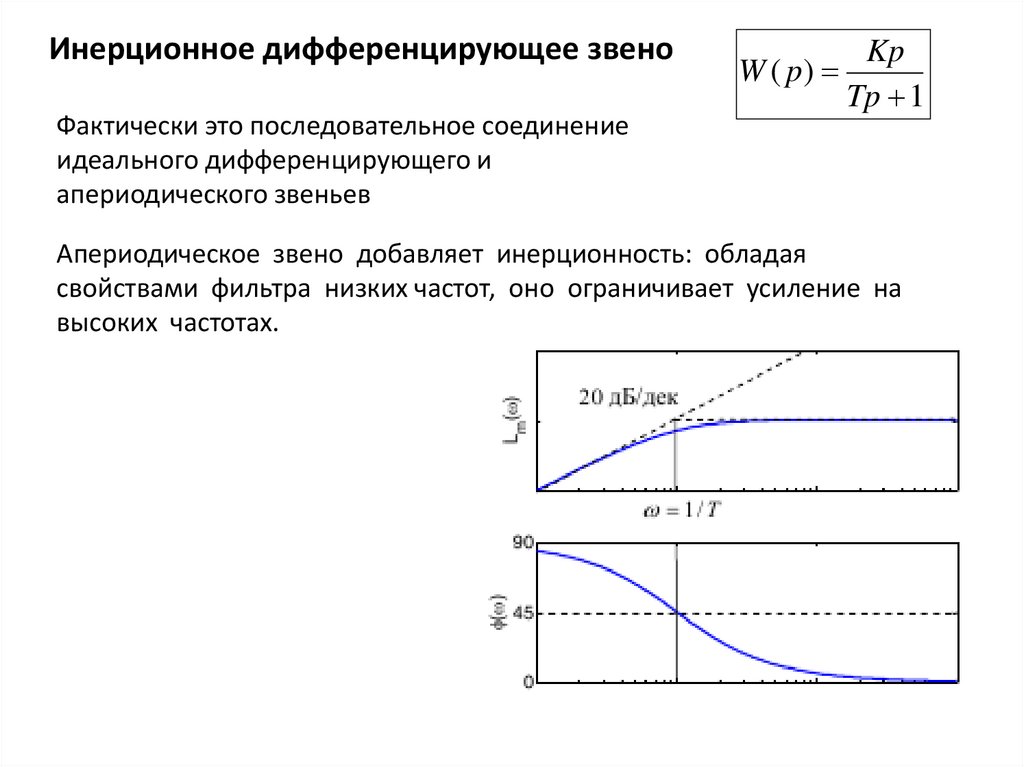
Инерционное дифференцирующее звено
Фактически это последовательное соединение
идеального дифференцирующего и
апериодического звеньев
W ( p)
Kp
Tp 1
Апериодическое звено добавляет инерционность: обладая
свойствами фильтра низких частот, оно ограничивает усиление на
высоких частотах.

28.

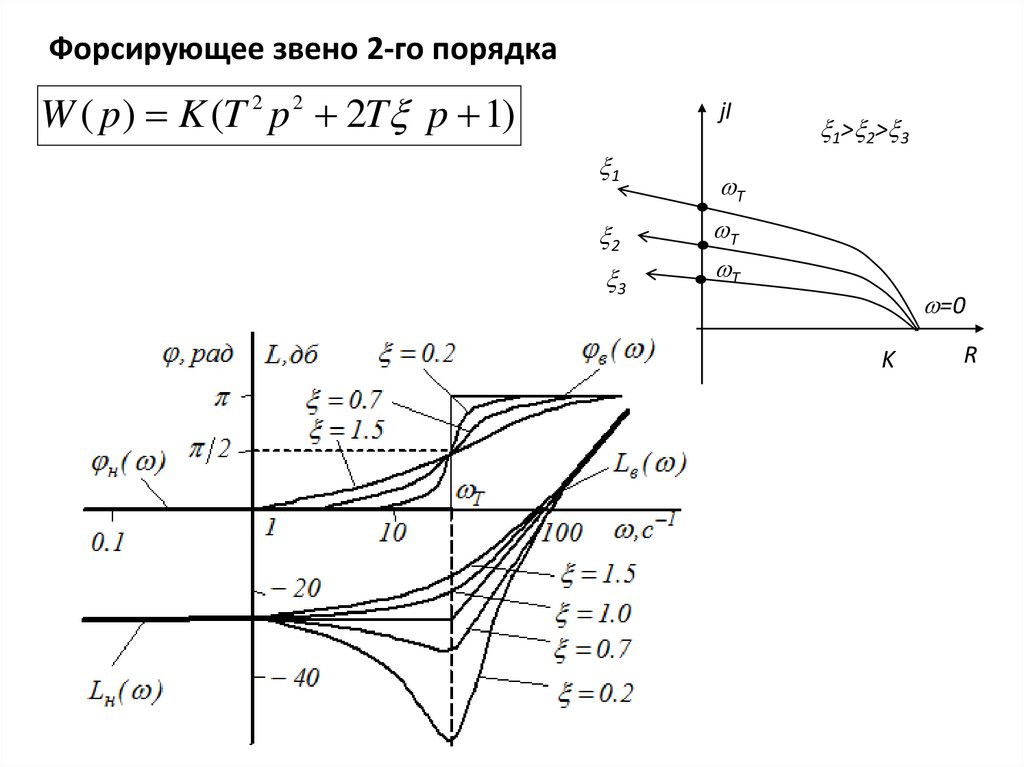
Форсирующее звено 2-го порядка
W ( p ) K (T 2 p 2 2T p 1)
jI
1
2
3
1> 2> 3
T
T
T
=0
K
R

29.

W(p)=K e-p
Звено запаздывания
При гармоническом входном сигнале запаздывание не
изменяет амплитуду, но вносит дополнительный
отрицательный сдвиг фазы.
W ( j ) Ke j
( ) argW ( j )
Wa ( ) W ( j ) K
Фазовая частотная характеристика звена запаздывания –
линейная функция частоты ω , чем больше частота, тем
больше фазовый сдвиг.
,рад L,дб
jI
40
K
-K
K
=0
-K
R
L( )
20
20lgK
- /2
-
( )

30.

Частотные характеристики соединений звеньев
1. АФЧХ последовательного соединения равна произведению АФЧХ всех
звеньев соединения:
k
W ( j ) Wi ( j ).
i 1
2. АЧХ последовательного соединения равна произведению АЧХ всех
звеньев соединения, т.к. модуль произведения равен произведению
модулей сомножителей
k
Wa ( ) Wai ( ).
i 1
3. ФЧХ последовательного соединения равна сумме ФЧХ всех звеньев
соединения, т.к. аргумент произведения равен сумме аргументов
сомножителей
k
( ) i ( )
i 1
4. ЛАХ последовательного соединения L( ) равна сумме ЛАХ всех
звеньев соединения, т.к. логарифм произведения равен сумме
k
логарифмов сомножителей:
L( ) Li ( )
Li( ) = 20lgWai( )
i 1

31.

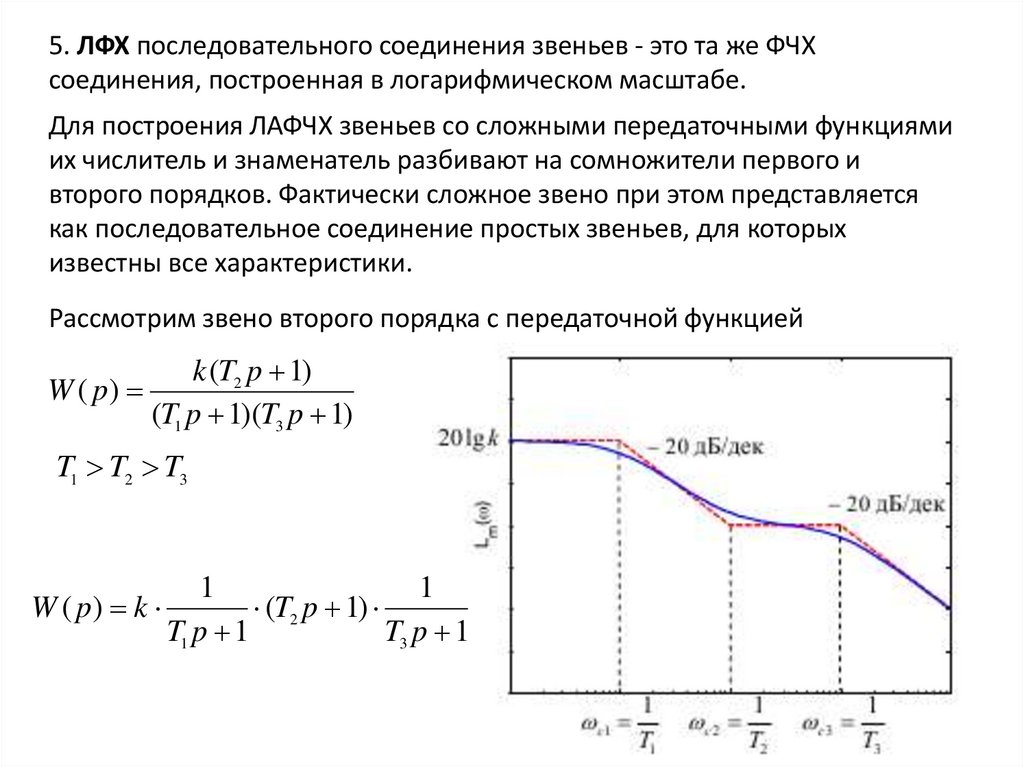
5. ЛФХ последовательного соединения звеньев - это та же ФЧХ
соединения, построенная в логарифмическом масштабе.
Для построения ЛАФЧХ звеньев со сложными передаточными функциями
их числитель и знаменатель разбивают на сомножители первого и
второго порядков. Фактически сложное звено при этом представляется
как последовательное соединение простых звеньев, для которых
известны все характеристики.
Рассмотрим звено второго порядка с передаточной функцией
k (T2 p 1)
W ( p)
(T1 p 1)(T3 p 1)
T1 T2 T3
1
1
W ( p) k
(T2 p 1)
T1 p 1
T3 p 1

32.

Самостоятельно
Частотные характеристики встречно-параллельного
соединения звеньев
Частотные характеристики параллельного соединения
звеньев