Временные и частотные характеристики

1.

Временные и частотные
характеристики

2.

Временные характеристики
Для того, чтобы можно было сравнивать поведение объектов и систем во времени, используют временные
характеристики или реакции на некоторые типовые воздействия, полученные при одинаковых условиях.
Переходная функция h(t)– это описание реакции объекта или системы на единичное входное воздействие,
полученной при нулевых начальных условиях.
Весовая функция w(t) – описание реакции объекта или системы на воздействие в виде δ-функции, полученной
при нулевых начальных условиях.
Единичная ступенчатая функция и δ-функция относятся к обобщенным функциям, обладающими рядом
специфических свойств.
Единичное ступенчатое воздействие (функция Хевисайда):
или
Дельта-функция ( -функция или функция Дирака):
Функция δ(t) описывает импульс, длительность которого стремится к 0, а площадь удовлетворяет условию:
.
Дельта-функция и единичная ступенчатая функция связаны соотношением

3.

Фильтрующие свойства дельта-функции δ(τ) и ее производных:
,…
,
.
Преобразования Лапласа от ступенчатой функции и дельта -функции:
В преобразованиях Лапласа переходная и весовая функции, полученные через определение передаточной функции
Ws)=Y(s)/V(s):
H(s)=W(s)/s , где 1/s - изображение по Лапласу единичной ступенчатой функции
H(s)=W(s)/s=L{h(t)}
L{w(t)}=W(s)
т.е. изображение по Лапласу весовой функции есть передаточная функция в изображениях по Лапласу.
Поскольку деление на s изображения функции соответствует интегрированию оригинала, то переходная функция
может быть выражена через весовую как
,
или
, т.е. весовая функция есть производная от переходной функции.

4.

Интегральная форма уравнения динамики
объекта или системы
Для описания объектов и систем наряду с дифференциальными уравнениями используют также интегральные
уравнения динамики, полученные из следующих преобразований:
Y(s)=W(s)X(s),
где X(s)- вход в преобразованиях Лапласа;
Y(s)- выход; W(s) – передаточная функция объекта или системы.
Выполняя обратное преобразование Лапласа от левой и правой частей выражения для Y(s), получим
y(t)=L-1{W(s)X(s)}
Обратное преобразование Лапласа от произведения изображений дает, как известно, интеграл свертки
оригиналов:
Эти выражения и есть интегральные уравнения динамики .
Линейные системы удовлетворяют принципу суперпозиции т.е. реакция системы на воздействие, состоящее из
суммы нескольких воздействий равна сумме реакций на каждое отдельно взятое воздействие (при одних и тех же
начальных условиях). Это позволяет разбивать системы на элементы с одним входом и упрощать их анализ.

5.

Комплексная частотная характеристика
Комплексной частотной характеристикой называется весовая функция объекта или системы в преобразованиях
Фурье, т.е.
Зачастую комплексная частотная характеристика (КЧХ) получается путем замены в передаточной функции
комплексного аргумента s=σ+jω на jω, что соответствует принятию σ=0. Это позволяет получать частотную характеристику
для расходящихся весовых функций, для которых преобразование Фурье не существует.
Комплексная частотная характеристика является комплексной функцией действительного аргумента –
круговой частоты ω, единица измерения которой – рад/с: ω=2πf.
КЧХ может бать представлена в виде суммы действительной и мнимой частей: W(jω)=ReW(jω)+jImW(jω), или
выражена в показательной форме через модуль комплексной функции или длину вектора комплексной функции и угол,
образуемый вектором с положительной действительной полуосью (смотри рисунок): W(jω)=A(ω)ejφ(ω)
A(ω)-модуль (длина) вектора;
φ(ω)-фазовый угол вектора.
•Фазовый угол, отсчитываемый против часовой стрелки, считают
•положительным, по часовой - отрицательным
Выражения для модуля КЧХ и фазового угла носят
названия амплитудной частотной характеристики A(ω)
(АЧХ) и фазовой частотной характеристики φ(ω) (ФЧХ):
т.е. A(ω)=|W(jω)|=
Комплексная частотная характеристика называется также амплитудно-фазовой частотной характеристикой
,

6.

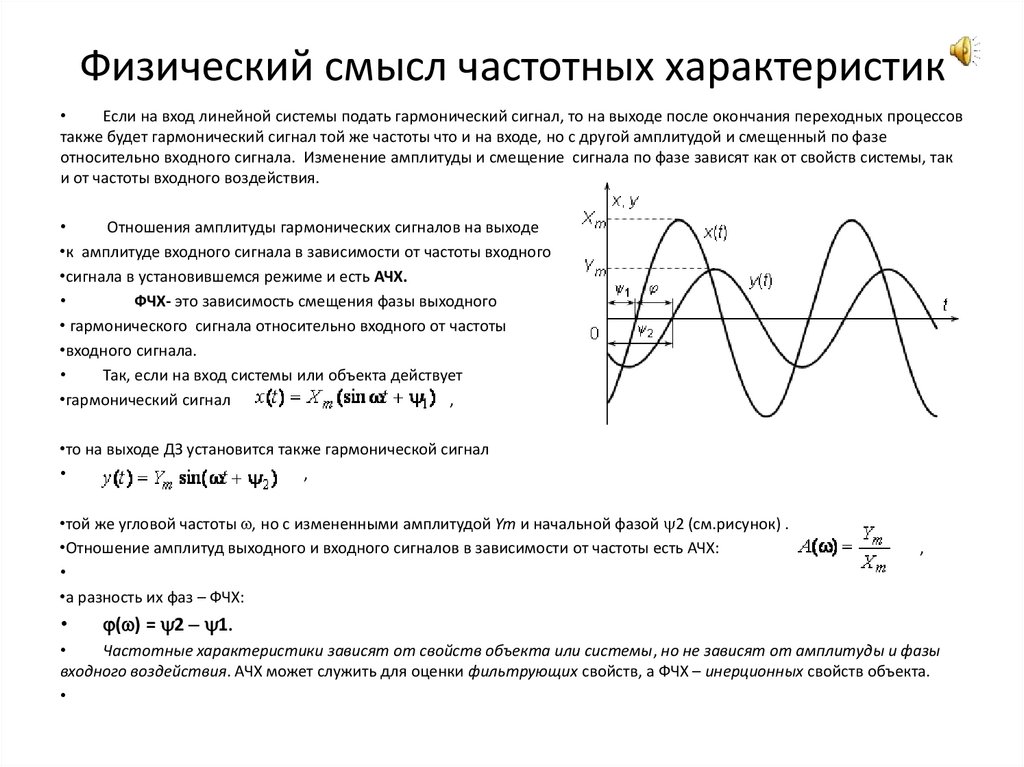
Физический смысл частотных характеристик
Если на вход линейной системы подать гармонический сигнал, то на выходе после окончания переходных процессов
также будет гармонический сигнал той же частоты что и на входе, но с другой амплитудой и смещенный по фазе
относительно входного сигнала. Изменение амплитуды и смещение сигнала по фазе зависят как от свойств системы, так
и от частоты входного воздействия.
Отношения амплитуды гармонических сигналов на выходе
•к амплитуде входного сигнала в зависимости от частоты входного
•сигнала в установившемся режиме и есть АЧХ.
ФЧХ- это зависимость смещения фазы выходного
• гармонического сигнала относительно входного от частоты
•входного сигнала.
Так, если на вход системы или объекта действует
•гармонический сигнал
,
•то на выходе ДЗ установится также гармонической сигнал
,
•той же угловой частоты , но с измененными амплитудой Ym и начальной фазой 2 (см.рисунок) .
•Отношение амплитуд выходного и входного сигналов в зависимости от частоты есть АЧХ:
•а разность их фаз – ФЧХ:
,
( ) = 2 1.
Частотные характеристики зависят от свойств объекта или системы, но не зависят от амплитуды и фазы
входного воздействия. АЧХ может служить для оценки фильтрующих свойств, а ФЧХ – инерционных свойств объекта.

7.

Логарифмические частотные характеристики
Достаточно часто также используется логарифмические частотные характеристики: ЛАЧХ (логарифмическая
амплитудная частотная характеристика) или ЛАХ: L(θ)=20lgA( ),
θ=lg(ω),
и ЛФЧХ (логарифмическая фазовая частотная характеристика) или ЛФХ: ψ(θ)= ( ).
• Эти характеристики удобны тем, что небольшим графиком может быть охвачен широкий диапазон частот. При этом
одинаково наглядно отображается изменение частотных свойств как на малых, так на средних и высоких частотах.
При построении амплитудной логарифмической характеристики по оси ординат откладывается логарифм
амплитудной характеристики, умноженный на 20, причем, изменения амплитуды в 10 раз соответствует изменению
ЛАХ на 20 децибел (дБ).
По оси абсцисс откладывается аргумент θ в декадах. Изменению частоты ω в 10 раз соответствует изменению θ на 1
декаду, нулевой частоте соответствует θ =lg0 = .
При построении фазовой логарифмической характеристики по оси ординат откладывается значения ФЧХ в радианах
или градусах, а по оси абсцисс - логарифм частоты в декадах.
Зачастую по оси абсцисс помимо логарифма частоты откладывается также и сама частота.
Частота, на которой убывающая ЛАХ пересекает ось абсцисс называется частотой среза ЛАХ.
Использование логарифмических характеристик упрощает анализ и синтез систем и делает более наглядным
графические изображения характеристик.
Помимо точных логарифмических характеристик используют также асимптотические или приближенные
характеристики. В этом случае ЛАЧХ и ЛФЧХ изображают отрезками прямых (асимптот) ( см.рисунок ).
Асимптоты ЛАЧХ имеют отрицательный и положительный наклон, кратный 20 дБ на декаду. Для построения
асимптотической ЛАЧХ проводят простые вычисления, так как любую асимптоту можно построить по двум точкам.
В англоязычной технической литературе и современных математических системах (MATLAB, Maple и др.) АФЧХ ,
АЧХ, ФЧХ называют диаграммами Найквиста, ЛАЧХ и ЛФЧХ называют диаграммами Боде (Bode diagramms).