Лекцiя 4. Геометричні характеристики поперечних перерізів

1.

ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНИХ ПЕРЕРІЗІВ
Величина нормальних напружень у поперечному перерізі розтягнутого (стиснутого) стержня залежить від площі цього
перерізу. Таким чином, площа поперечного перерізу є геометричною характеристикою, що визначає напруження при
розтягуванні (стисканні). У випадку інших видів напружено-деформованого стану (згин, кручення), напруження залежать не від
площі, а від деяких інших геометричних характеристик поперечного перерізу.
Площа поперечного перерізу:
A = ò dA.
A
yC
y
Статичні моменти площі поперечного перерізу:
dy
dA
C
y xC
yC
O
x dx
xC
S x = ò ydA; S y = ò xdA.
A
A
x Статичні моменти використовуються при
визначенні положення центру ваги:
Визначення координат центру ваги.
Використаємо, наприклад, метод розбиття
на декілька елементарних елементів:
S yi å xi Ai
å
xC =
=
;
A
A
å i å i
xC =
Sy
A
; yC =
Sx
.
A
S xi å yi Ai
å
yC =
=
.
A
A
å i å i
Тут xi, yi - координати центрів ваги простих фігур, для яких вони відомі або легко
знаходяться.
Осі, що проходять через центр ваги фігури, називаються центральними. Слід відмітити,
що відносно центральних осей, статичні моменти площі перетворюються в нуль.

2.

Методи визначення центра ваги складних фігур
1. Метод розбиття – складна фігура розбивається на сукупність простих фігур, для
яких відомі положення центра ваги або вони легко визначаються:
y
1
xC =
2
x
x1
å xi Ai = x1 A1 + x2 A2
A1 + A2
å Ai
x2
2. Метод від’ємних площ – так само, як і в методі розбиття, складна фігура розбивається
на сукупність простих фігур, для яких відомі положення центра ваги або вони легко
визначаються, але при наявності отворів або пустот зручно їх представлення у вигляді
«від’ємних» областей.
Наприклад, дану фігуру замість розбиття на 4 звичайних прямокутника, можна
представити як сукупність двох прямокутників, один з яких має негативну площу:
y
xC =
2
1
x
x1
x2
å xi Ai = x1 A1 + x2 (- A2 )
A1 + (- A2 )
å Ai
Примітка. Оскільки координата, наприклад, x2, може бути
негативна, то не слід представляти цей вираз з використанням
різниць:
x A -x A
xC = 1 1 2 2
A1 - A2

3.

3. Метод симетрії – за наявності у фігури осі або площини симетрії, центр ваги лежить на
цій осі або в цій площині. З урахуванням цієї властивості зменшується кількість
координат центру ваги, що підлягають визначенню.
4. Метод інтегрування – за наявності у фігури досить простого контуру, що описується
відомим рівнянням (коло, парабола тощо), вибирається елементарна площадка або
смужка і виконується аналітичне інтегрування. При більш складному контурі, який
може бути розбитий на більш прості граничні відрізки використовується попередньо
метод розбиття. При складнощах з аналітичним інтегруванням використовуються
чисельні методи інтегрування.
5. Метод підвішування – експериментальний метод, заснований на тому, що при
підвішуванні тіла або фігури за яку-небудь довільну точку центр ваги знаходиться на
одній вертикалі з точкою підвісу. Для визначення положення центра ваги плоскої
фігури достатньо її підвісити по черзі за дві будь-які точки і прокреслити відповідні
вертикалі, наприклад, за допомогою виска. Тоді точка на перетині цих прямих
відповідає положенню центру ваги фігури.

4. Порядок вирішення задач на визначення центра ваги:

5.

Приклад 1 - Визначити положення центру ваги куткового поперечного перерізу.
4
y
1. Вибираємо систему координат x, y з початком
в нижньому лівому куті перерізу.
1
C
12
O
2
4 x
x1
x2
20
2. Розбиваємо фігуру на два прямокутники,
обчислюємо площі і координати центрів ваги кожного:
A1 = 4 × 12 = 48;
x1 = 2; y1 = 6;
20 - 4
+ 4 = 12; y2 = 2;
2
3. Обчислюємо статичні моменти і координати центру ваги всього перерізу:
S y1 = x1 A1 = 2 × 48 = 96;
S x1 = y1 A1 = 6 × 48 = 288;
A2 = (20 - 4) × 4 = 64;
S x 2 = y2 A2 = 2 × 64 = 128;
x2 =
S y 2 = x2 A2 = 12 × 64 = 768;
4. Обчислюємо координати центру ваги всього перерізу:
xC =
å S yi = S y1 + S y 2 = 96 + 768 = 864 = 7,71.
å Ai A1 + A2 48 + 64 112
yC =
å S xi = S x1 + S x 2 = 288 + 128 = 416 = 3,71.
å Ai A1 + A2 48 + 64 112

6.

Момент інерції площі поперечного перерізу – це інтеграл
(сума) добутків елементарних площадок на квадрат відстані
від цих площадок до розглядуваної осі (точки).
I x = ò y dA;
2
A
I xy = ò xydA
I y = ò x dA
2
dy
- осьові моменти інерції площі.
A
y
- відцентровий момент інерції площі.
O
A
I r = ò ( x 2 + y 2 )dA = ò r 2 dA
A
y
dA
r
x
dx
x
- полярний момент інерції площі.
A
Моменти інерції площі використовуються при визначенні напружень при згині і крученні.
Відцентровий момент інерції щодо осей, одна з яких збігається з віссю симетрії,
дорівнює нулю. Це твердження базується на тому, що в цьому випадку елементарній
площі dA з координатами (x, y) завжди буде відповідати така ж площа з координатами (-x, y)
або (x, -y). Підсумовування (інтегрування) похідних xydA дасть нуль. Далі буде доведено, що
для будь-якої, в тому числі несиметричної, фігури можна знайти таке положення осей, при
якому відцентровий момент інерції перетворюється в нуль.
Полярний момент інерції не залежить від орієнтації координатних осей х, у та завжди
дорівнює сумі осьових моментів інерції:
I r = ò r 2 dA = ò ( x 2 + y 2 )dA = ò x 2 dA + ò y 2 dA = I y + I x .
A
A
A
A

7.

Моменти інерції площі найпростіших перерізів
Прямокутник
y
2
C
yC
b
dy
h
xC
y
x
2
0
A
dA
xC
h
I x = ò y dA = ò y bdy = b ò
yC
h
0
3 h
y
y dy = b
3
2
0
bh3
=
.
3
Відомо, що центр ваги прямокутника знаходиться на перетині
осей симетрії (xC = b / 2, yC = h / 2).
Для обчислення моментів інерції відносно центральних осей
слід врахувати, що координата y вимірюється від центральної
осі xc. Тобто необхідно змінити межі інтегрування:
I Xc
3 h/2
y
=ò
y bdy = b ò
y dy = b
-h / 2
-h/ 2
3
h/2
Аналогічно одержимо для інших осей:
2
h/2
2
hb3
hb3
Iy =
; IYc =
.
3
12
Відцентровий момент інерції (за рахунок симетрії):
I XcYc = 0.
-h / 2
bh3
=
.
12

8.

Трикутник
у
Елементарна площа має змінну ширину
і залежить від її координати по осі y:
dA
by
h- y
h- y
=
; by =
b;
b
h
h
h- y
dA = by dy =
bdy.
h
I x = ò y 2 dA = ò
A
h
0
yC
xC
by
C
x
b
h
3
æ
ö
h
b
b
y
y
bh
h
y
2
3
.
y2
bdy = ò0 (hy - y )dy = ç h ÷ =
h
h
3
4
12
h
è
ø0
3
2h / 3
3
æ
ö
b 2h / 3 2
b
y
y
bh
= ò
(hy - y 3 )dy = ç h =
.
÷
h
/
3
h
hè 3
4 ø
36
-h /3
3
Момент інерції щодо центральної осі yC:
IYc = 2 IYc (b / 2)
h
xC
yC
Момент інерції відносно центральної осі xC:
I Xc
dy
y
h(b / 2)3 hb3
=2
=
.
12
48
4
4

9.

Круглий переріз
y
Обчислимо спочатку полярний момент інерції:
dr
R
r
0
pR 4 pD 4
=
=
.
2
32
pR 4 pD 4
Ix = I y =
=
=
.
2
4
64
Ir
Кільцевий переріз
y
Достатньо змінити межі інтегрування:
dr
r
2
Моменти інерції щодо центральних
осей з урахуванням симетрії:
dA
R
4 R
r
I r = ò r dA = ò r 2prd r = 2p
4
A
0
2
x
R
4 R
r
x
r
I r = 2p
4
r
p( R 4 - r 4 ) p( D 4 - d 4 )
=
=
.
2
32
Моменти інерції щодо центральних осей
з урахуванням симетрії:
dA
p( R 4 - r 4 ) p( D 4 - d 4 )
Ix = I y =
=
=
.
2
4
64
Ir

10.

Моменти інерції площі складених перерізів обчислюються, так само як і при
обчисленні координат центру ваги, методом розбиття на прості фігури, для яких відомі
або легко обчислюються координати центрів ваги і моменти інерції.
Наприклад, момент інерції кільцевого перерізу може бути обчислений як різниця
моментів інерції круглого суцільного перерізу радіусу R і такого ж перерізу, але радіуса r.
Зауважимо, що при додаванні моментів інерції по кожній з координатних осей для кожної
з фігур моменти інерції повинні обчислюватися відносно осей, які є загальними для
розглянутого перерізу і всіх складових фігур. Звідси випливає необхідність оперувати
формулами, що дозволяють переходити від одних до інших осей.
ЗАЛЕЖНІСТЬ МІЖ МОМЕНТАМИ ІНЕРЦІЇ ПРИ ПАРАЛЕЛЬНОМУ ПЕРЕНОСІ ОСЕЙ
Y1
2
2
2
2
y
dA
+
2
a
ydA
+
a
dA
.
I X 1 = y1 dA = ( y + a ) dA =
y
ò
ò
ò
A
ò
A
A
x1 = b + x;
A
Ix
y1 = a + y
Аналогічно для осі Y1 і X1Y1 :
ò
A
Sx
dA
x1
A
y1
O
I X 1 = I x + 2aS x + a 2 A.
2
IY1 = I y + 2aS y + b A.
O1 b
x
A
Формули спрощуються, якщо вихідні осі є центральними, т.я. SxC = SyC = 0:
I X 1 = I xC + a 2 A.
IY1 = I yC + b 2 A.
x
a
I X 1Y1 = ò x1 y1dA = ò ( y + a )( x + b)dA = I xy + aS y + bS x + abA.
A
y
I X 1Y1 = I xC yC + abA.
X1

11.

ЗАЛЕЖНІСТЬ МІЖ МОМЕНТАМИ ІНЕРЦІЇ ПРИ ПОВОРОТІ ОСЕЙ
v
Координати елементарної площадки dA в
системі координат u, v виражаються через
вихідні координати x, y лінійними залежностями:
y
x dA
u
xcos
u = x cos + y sin ;
v = - x sin + y cos .
y
u
ycos
xsin
x
ysin
x
O1
v
Осьові моменти інерції щодо осей u і v:
2
2
2
2
I u = ò v 2 dA = ò ( y cos - x sin ) 2 dA = cos ò y dA - 2sin cos ò xydA + sin ò x dA.
A
A
sin 2
A
A
A
Iy
I xy
Ix
I u = I x cos 2 + I y sin 2 - I xy sin 2 .
2
2
2
2
I v = ò u 2 dA = ò ( y sin + x cos ) 2 dA = sin ò y dA + 2sin cos ò xydA + cos ò x dA.
A
A
I u + I v = I x + I y = const
Сума осьових моментів інерції щодо двох
перпендикулярних осей не залежить від кута
і при повороті осей зберігає постійне значення.
sin 2
A
Ix
A
A
I xy
I v = I x sin 2 + I y cos 2 + I xy sin 2 .
Iy

12.

13.

ГОЛОВНІ ОСІ ТА ГОЛОВНІ МОМЕНТИ ІНЕРЦІЇ
Отримані залежності показують, що при зміні кута повороту осей значення моментів
інерції змінюються, при цьому сума осьових моментів інерції залишається постійною.
Це означає, що можна визначити таке положення осей, при якому один з осьових
моментів досягає максимального значення, а інший - відповідно мінімального значення.
Максимальні та мінімальні осьові моменти інерції називаються головними
моментами інерції, а осі, щодо яких вони обчислюються, - головними осями.
Для визначення положення головних осей досить прирівняти до нуля першу похідну
осьового моменту інерції по куту повороту:
I u = I x cos 2 + I y sin 2 - I xy sin 2 .
¶I u
= I x (-2cos )sin + I y 2sin cos - I yx 2cos 2 = - ( I x - I y )sin 2 - 2 I xy cos 2 = 0.
¶
sin 2
sin 2
Отриманий результат показує, що для шуканого положення осей відцентровий момент
перетворюється в нуль.
Звідси можна знайти положення головних осей:
tg2 = -
2 I xy
Ix - I y
Оскільки тангенс має однакові значення для кутів, що
відрізняються один від одного на 1800, отриманий вираз
визначає два положення осей, що відрізняються один від
одного на 900.
Таким чином, обидві головні осі взаємно перпендикулярні.
.

14.

Для довідки. Визначення головних моментів інерції без тригонометричних формул
I u = I x cos 2 + I y sin 2 - I xy sin 2 .
cos 2 =
Iu =
tg2 = -
1 - cos 2
1 + cos 2
sin 2 =
2
2
Ix + I y
2
+
Ix - I y
2
Iu =
cos 2 - I xy sin 2
2 I xy
I xy
Ix - I y
Ix + I y
2
+
I x - I y sin 2
=2 cos 2
Ix - I y
2
1
.
cos 2
1
= ± 1 + tg 2 2
cos 2
tg2 = -
2 I xy
Ix - I y
1
1
2
=±
( I x - I y ) 2 + 4 I xy
.
cos 2
Ix - I y
Підставляючи останній вираз і скорочуючи
різницю моментів інерції отримуємо остаточно:
I max =
min
Ix + I y
2
1
±
2
( Ix - I y )
Знак плюс перед другим доданком відноситься до максимального моменту,
знак мінус - до мінімального.
2
2
+ 4 I xy
.

15.

Обчислення моментів інерції складних фігур - виконується в наступному порядку:
1.Переріз розбивається на частини, для яких відомі координати центрів ваги і моменти
інерції або легко знаходяться.
2.Вибираються початкові осі, щодо яких обчислюються координати центру ваги перерізу.
3.Обчислюються координати центра ваги перерізу.
4.Проводяться центральні осі (що проходять через центр ваги перерізу), щодо яких
обчислюються моменти інерції.
5.Обчислюються осьові і відцентрові моменти інерції всього перерізу щодо центральних
осей.
6.Обчислюються головні центральні моменти і визначається положення головних осей.
Приклад 1 - Визначити головні центральні моменти інерції і положення головних осей
кутикового поперечного перерізу.
y
t2
yC
1
C
h
O
1
xC
2
t x
x1
x2
a
x × A + x2 × A2
t
h
xc = 1 1
x1 = , y1 = , A1 = h × t
A1 + A2
2
2
;
a+t
t
y1 × A1 + y 2 × A2
x2 =
, y 2 = , A2 = ( a - t ) × t yc =
2
2
A1 + A2
( a - t) × t3 + A × a2 ,
t × h3
+ A1 × a12 +
2
2
12
12
3
h × t3
t × ( a - t)
2
2
I yC = å ( I yВЛ + A × b ) =
+ A1 × b1 +
+ A2 × b22 ,
12
12
I xyC = å ( I xyВЛ + A × a × b ) = 0 + A1 × a1 × b1 + 0 + A2 × a2 × b2 .
I xC = å ( I xВЛ + A × a 2 ) =
tg 2 = -
2 I xy
Ix - Iy
.
I u = I x cos 2 + I y sin 2 - I xy sin 2 .
I u = I x sin 2 + I y cos 2 + I xy sin 2 .
a1 = y1 - yc
a 2 = y 2 - yc
b1 = x1 - xc
b2 = x2 - xc

16.

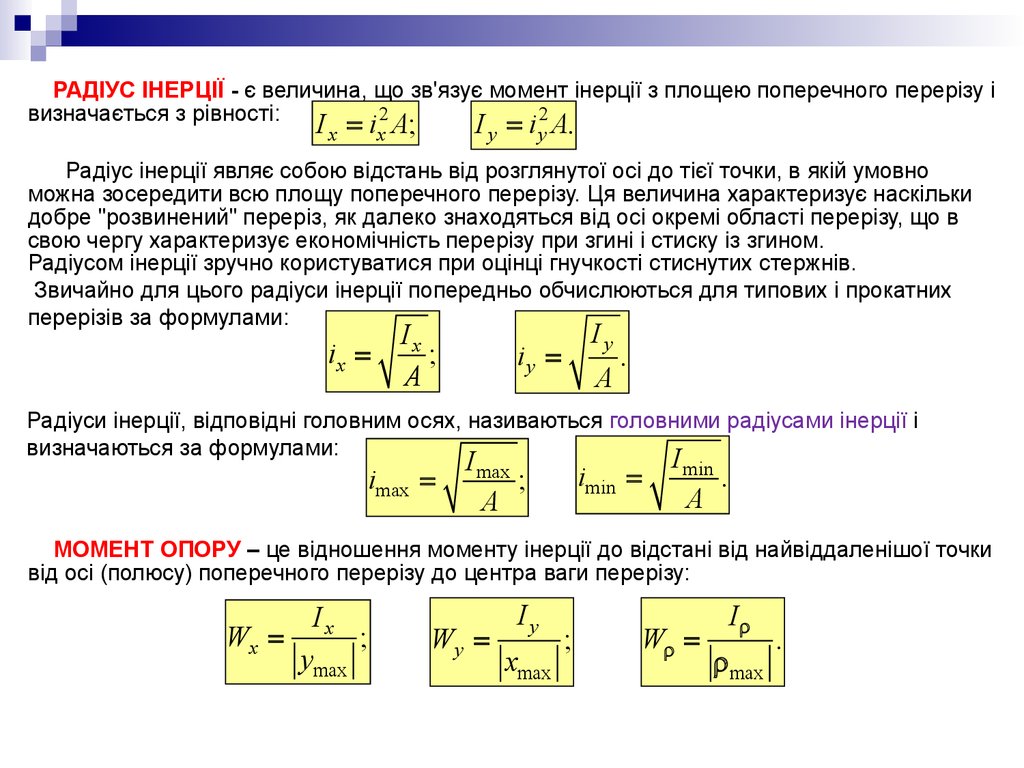
РАДІУС ІНЕРЦІЇ - є величина, що зв'язує момент інерції з площею поперечного перерізу і
2
2
визначається з рівності:
I x = ix A;
I y = i y A.
Радіус інерції являє собою відстань від розглянутої осі до тієї точки, в якій умовно
можна зосередити всю площу поперечного перерізу. Ця величина характеризує наскільки
добре "розвинений" переріз, як далеко знаходяться від осі окремі області перерізу, що в
свою чергу характеризує економічність перерізу при згині і стиску із згином.
Радіусом інерції зручно користуватися при оцінці гнучкості стиснутих стержнів.
Звичайно для цього радіуси інерції попередньо обчислюються для типових і прокатних
перерізів за формулами:
ix =
Ix
;
A
Iy
iy =
A
.
Радіуси інерції, відповідні головним осях, називаються головними радіусами інерції і
визначаються за формулами:
imax =
I max
;
A
imin =
I min
.
A
МОМЕНТ ОПОРУ – це відношення моменту інерції до відстані від найвіддаленішої точки
від осі (полюсу) поперечного перерізу до центра ваги перерізу:
I
Wx = x ;
ymax
Wy =
Iy
xmax
;
Wr =
Ir
r max
.

English Русский Rules