Косий згин. Лекція 9

1. 1. Косий згин.

Лекція 9.
1. Косий згин.
СКЛАДНІ ВИДИ ОПОРУ: 1. Косий згин.
2. Позацентровий стиск.
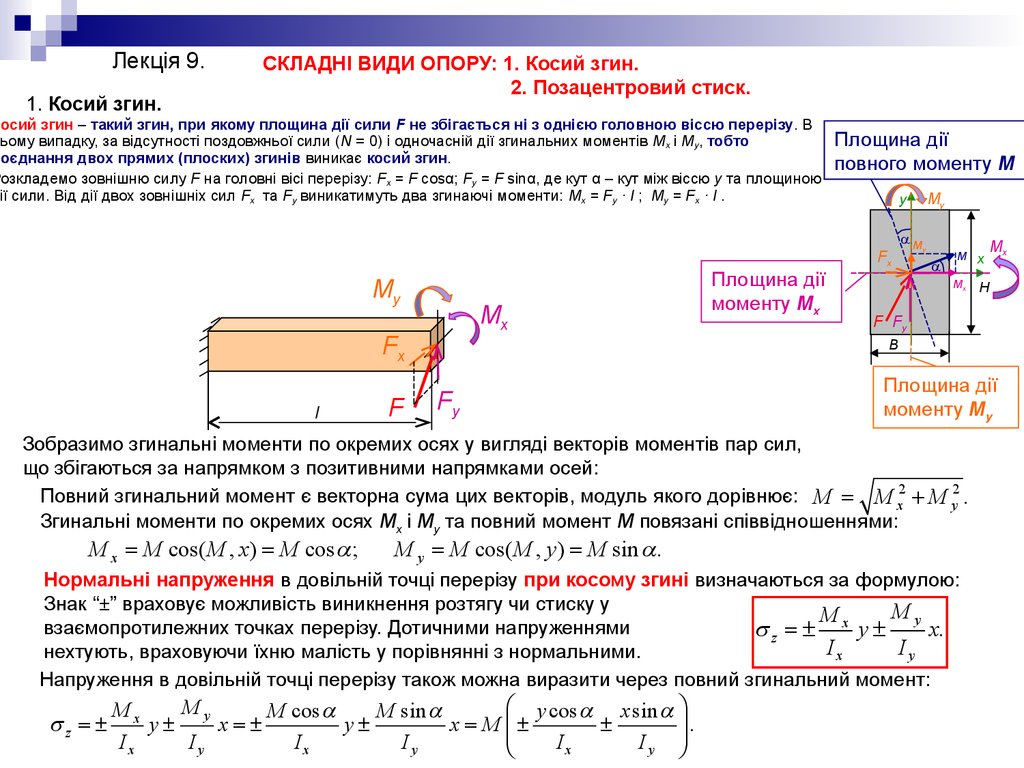
Косий згин – такий згин, при якому площина дії сили F не збігається ні з однією головною віссю перерізу. В
ьому випадку, за відсутності поздовжньої сили (N = 0) і одночасній дії згинальних моментів Mx і My, тобто
поєднання двох прямих (плоских) згинів виникає косий згин.
Розкладемо зовнішню силу F на головні вісі перерізу: Fx = F cosα; Fy = F sinα, де кут α – кут між віссю у та площиною
дії сили. Від дії двох зовнішніх сил Fx та Fу виникатимуть два згинаючі моменти: Mx = Fy · l ; My = Fx · l .
My
Mx
Fx
l
F
Площина дії
моменту Mx
Площина дії
повного моменту M
My
y
Fx
aM
у
a
M
Mx
H
B
Площина дії
моменту My
Fy
M y = M cos( M , y ) = M sin a .
Нормальні напруження в довільній точці перерізу при косому згині визначаються за формулою:
Знак “±” враховує можливість виникнення розтягу чи стиску у
M
M
взаємопротилежних точках перерізу. Дотичними напруженнями
s z = ± x y ± y x.
Ix
Iy
нехтують, враховуючи їхню малість у порівнянні з нормальними.
Напруження в довільній точці перерізу також можна виразити через повний згинальний момент:
sz = ±
Mx
F Fy
Зобразимо згинальні моменти по окремих осях у вигляді векторів моментів пар сил,
що збігаються за напрямком з позитивними напрямками осей:
Повний згинальний момент є векторна сума цих векторів, модуль якого дорівнює: M = M x2 + M y2 .
Згинальні моменти по окремих осях Мх і Му та повний момент М повязані співвідношеннями:
M x = M cos( M , x) = M cos a ;
x
æ y cos a x sin a
My
Mx
M cos a
M sin a
y±
x=±
y±
x = M ç±
±
ç
Iх
Iy
Ix
Iy
I
Iy
x
è
ö
÷÷ .
ø

2.

Визначимо положення нульової лінії – геометричного місця точок, у яких напруження рівні нулю,
прирівнявши вираз для визначення напружень до нуля:
æ y cos a x sin a
sz = M ç
+
ç Ix
Iy
è
ö
÷÷ = 0.
ø
y cos a x sin a
+
= 0.
Ix
Iy
y = -tga
Ix
x.
Iy
Рівняння нульової лінії являє собою рівняння прямої, що проходить через початок координат.
При однакових Іх та Іу косий згин не спостерігається. Тангенс кута β нахилу нульової лінії дорівнює:
tg b = -tga
Ix
.
Iy
При цьому знак “-” означає, що площина дії сили та нульова лінія завжди лежать в різних четвертях.
Площина дії
повного моменту M
y
β
aM
n
β
у
a
M
Mx
x
H
n
B
Для балок, що працюють в основному на вертикальне навантаження, висоту перерізу приймають
більшу ніж ширину. Тоді Ix > Iy і кут нахилу нульової лінії β більше кута нахилу повного згинального
моменту α. Це означає, що повний прогин не збігається з площиною дії повного моменту. Звідси і
походить назва косого згину.

3.

Підбір поперечного перерізу при косому згині.
Запишемо умову міцності при косому згині:
Винесемо 1/Wx за дужки:
Mx My
sz =
+
£ [s ].
Wx Wy
ö
Wx
1 æ
M
+
×
M
= s ,
ç x
y÷
÷ [ ]
Wx çè
Wy
ø
Wx =
ö
W
1 æ
çç M x + x × M y ÷÷
Wy
[s ] è
ø
формула підбору поперечного перерізу при косому згині.
Після підбору розмірів перерізу при косому згині перевірка
умови міцності обов’язкова. Тут приймають: Wx h
=
- для прямокутного перерізу;
Wy b
Wx
= 6...11
Wy
- для прокатних профілів.
Для довідки. Навіть незначне відхилення від вертикалі навантаження або відхилення від вертикалі
положення перерізу призводить до досить значного збільшення напружень в поперечному перерізі і
деформацій (прогинів) таких балок.
Наприклад, нехай відхилення від вертикалі поперечного перерізу балки двотаврового перерізу №20 з
моментами опору Wx = 184 см3, Wy = 23.1 см3 та моментами інерції Ix = 1840 см4, Iy = 115 см4 складає
всього 2о. Тоді максимальні напруження збільшуються на 27.7% від розрахункового значення (без
відхилення по вертикалі), а максимальний прогин - на 14.5%.

4. 2. Позацентровий стиск.

■
Під час одночасної дії поздовжньої сили (виникнення деформацій розтягу чи стиску) і згинальних
моментів (виникнення деформацій згину) у поперечних перерізах стержня виникатимуть нормальні
напруження, які можуть обчислюватися окремо і додаватися відповідно до принципу незалежності дії сил:
sz
y
x
My
=
N
A
x Mx
-
y
N
z
My
Mx
x
y +
Iy
Ix
+
+
+
+
sz =
+
+
My
N Mx
+
y+
x,
A Ix
Iy
тут x, y - координати точки, в якій знаходяться напруження.
Іноді формулу для визначення напружень при спільній дії поздовжньої сили і згинальних моментів із
врахуванням можливості виникнення розтягу чи стиску у взаємопротилежних точках перерізу
My
записують у вигляді:
N Mx
sz = ±
A
±
Ix
y±
Iy
x,
тут x, y - відстані до точки від координатних осей, в якій знаходяться напруження;
згинальні моменти беруться за модулем;
знаки доданків присвоюються за характером деформацій (розтягу або стиску) від кожного з
моментів.
Вираз показує, що напруження в точці лінійно залежать від координат x та y. Для визначення
максимальних напружень, необхідно знайти точку, максимально віддалену від нульової (нейтральної
осі), що зазвичай співпадає з координатними осями, проведеними через центр ваги перерізу.
Тоді вираз для визначення максимальних напружень прийме вигляд:
sz
max
=
N Mx My
+
+
.
A Wx Wy

5.

Для отримання рівняння нульової лінії слід прирівняти
вираз для визначення напружень до нуля:
My
N Mx
+
y+
x = 0.
A Ix
Iy
Нульову лінію можна побудувати за допомогою відрізків,
N × Iy
що відсікаються цією прямою на координатних осях,
x0 = ;
почергово прирівнявши до нуля кожну з координат:
My × A
Таким чином, максимальні напруження виникають у точці,
розташованій у правому верхньому куті розглянутого
прямокутного поперечного перерізу, яка найбільш віддалена
від нульової лінії:
sz
max
N M H My B N Mx My
= + x× +
× = +
+
.
A Ix 2
I y 2 A Wx Wy
y0 = -
y
n
sz
max
s Mx
σmax
sN
+
x0
x
y0
+
σmax
H
-
Цей же результат для даного простого поперечного перерізу можна
отримати без знаходження положення нульової лінії, розглядаючи
знаки доданків напружень у кутових точках:
My
My
N M
N M
= ± x ×y±
×x = ± x ±
.
A Ix
Iy
A Wx Wy
N × Ix
.
Mx × A
B
n
+
+
sMy
sN

6.

Таким чином, позацентровий розтяг-стиск виникає при дії розтягуючої або стискаючої сили F, точка прикладення якої не
збігається з віссю стержня, а має деякі зміщення щодо центральних осей (ексцентриситети) xF і yF. При перенесенні сили
паралельно самій собі в новий центр виникатимуть згинаючі моменти Mx і My:
■
F
My
Mx
xF
yF
z
y
C
x
Тобто, в довільному перерізі стержня маємо внутрішні зусилля:
N = - F; Mx = - F ∙ yF; My = - F ∙ xF.
Умова міцності при позацентровому стиску запишеться так:
M
N M
s z = + x + y £ [s ] .
A Wx Wy
- F - F × yF
- F × xF
+
× y0 +
× x0 = 0
A
Ix
Iy
Рівняння нульової лінії приймає вигляд:
або з використанням радіусів інерції перерізу:
Iy
I
i = x ; i y2 =
Þ
A
A
2
x
1+
yF × y0 xF × x0
+ 2 = 0.
ix2
iy
i y2
ix2
x0 = - ; y0 = - .
xF
yF
При проектуванні масивних стиснутих стійок з матеріалів, що мають межу міцності на розтяг значно
менше ніж на стиск (наприклад, бетон, цегляна кладка, чавун) необхідно забезпечити в поперечному
перерізі відсутність розтягуючих напружень, тобто нульова лінія не повинна перетинати контур
поперечного перерізу. Таким чином, постає питання про допустимі зміщення стискаючої сили щодо
центральних осей поперечного перерізу.
Область допустимих положень поздовжньої сили, при яких в усьому перерізі виникають
напруження одного знаку, називається ядром перерізу.

7.

Побудова
ядра
перерізу.
для простоти
прямокутний
переріз
розміром
BxH:в якій
Рівняння
нульової
лінії
показує,Розглянемо
що координати
точки прикладання
сили
і координати
точки,
3
2
3
I y HBв тому,
напруження
дорівнюють
нулю,2 володіють
Радіуси інерції
перерізу:
1 щоBякщо силу
I x BH "взаємністю",
1
H 2 що виражається
2
i
=
=
×
=
.
i
=
=
×
=
;
y
x
помістити в будь-яку точку знайденої
нульової лінії, то нова нульова
через
A лінія
12 пройде
BH обов'язково
12
A
12 BH 12
точку, в якій була раніше сила.
Задамо положення нульової лінії по верхньому обрізу перерізу і визначимо координати точки
Отже при русі точки прикладання сили по прямій, що збігається з первісною нульовою лінією,
прикладання поздовжньої сили, що відповідають цій нульової лінії.
наприклад, по верхньому краю перерізу, нова нульова лінія буде продовжувати проходити через ту ж
H
точку, обертаючись навколоyнеї,= оскільки
нульової лінії залишається в силі.
, x01 =рівняння
¥;
Рівняння нульової лінії:
01
2
З рівнянь нульової лінії можна визначити координати сили:
xF1 = -
i
2
y
¥
= 0;
2
x
2
i
H 2
H
yF1 = =× =- .
y01
12 H
6
xF
Задамо положення нульової лінії по правому краю перерізу і визначимо координати
точки прикладання поздовжньої сили, що відповідають цій нульової лінії.
B
, y02 = ¥;
2
ix2
B2 2
B
=× = - ; yF2 = - = 0.
12 B
6
¥
Рівняння нульової лінії:
xF2 = -
i y2
x02
x02 =
n2
y
n1 n4
3
H
4
2
n1
x
yF
1
n3
n3
B
n4
n2
Потім, повторюючи подібні дії для двох інших сторін перерізу, отримуємо
взаємопротилежні положення поздовжньої сили. Отримані точки є вершинами ядра
перерізу.
Можна довести, що при зміні положення точки прикладання поздовжньої сили нульової лінії по прямій,
що сполучає дві вершини ядра перерізу, нульова лінія, залишаючись дотичною до перерізу, лише
повертається. Або навпаки, при повороті нульової лінії навколо кута перерізу (n1 - n1 переходить в n2 n2) точка прикладання поздовжньої сили переміщається по прямій, що з'єднує вершини 1 і 2: