Similar presentations:
Аналіз зв’язку між змінними: кореляція і регресія
1. Аналіз зв’язку між змінними: кореляція і регресія
Поняття кореляційного зв’язку.Кореляційний і регресійний аналіз.
2. Параметричний кореляційний аналіз.
3. Непараметричний кореляційний аналіз.
4. Регресійний аналіз. Лінійна регресія.
1.
2. 1. Поняття регресійного аналізу.
Функціональний зв’язок –вид зв’язку, коли
конкретному значенню
одного показника відповідає
єдине значення іншого
показника
Кореляційний зв’язок –
вид зв’язку, коли
конкретному значенню
одного показника відповідає
деякий діапазон значень
іншого показника.
Зв’язок поділяють :
- за напрямком: прямий і
зворотній,
- за силою: слабкий, середній
і сильний,
- за формою: лінійний
(рівномірна зміна х та y) і
нелінійний (рівномірна зміна
х та нерівномірна зміна у)
3. Кореляційний аналіз
Кореляційний аналіз – цесукупність статистичних
прийомів, за допомогою
яких досліджується зв’язок
між ознаками
Параметричний коефіцієнт r
– коли обидві вибірки вибрані з
нормально розподілених
сукупностей,
Непараметричний
коефіцієнт r – коли або хоч
одна з вибірок взята з
генеральної сукупності,
розподіленої не за нормальним
законом, або розподіли
невідомі.
4. Коефіцієнт кореляції Пірсона
Емпіричний коефіцієнтКоефіцієнт кореляції
(вибірковий r, генеральний ρ)
– показник, який показує силу
і напрямок зв’язку між двома
параметрами (наприклад, х і
у)
Коваріація – усереднена
величина добутків відхилень
кожної пари змінних від їх
середніх; вказує, в якій мірі
більшим (меншим) значенням
хі відповідають більші (менші)
значення уі.
кореляції:
n
rxy
( x x )( y
i 1
i
n x y
i
y)
0<|r|<1
NB!: характеризує тільки
лінійний зв’язок
Коваріація:
n
( xi x )( yi y )
cov i 1
n
NB!: не коректно вживати для
величин х і у з різною
розмірністю
5. Напрямок і сила зв’язку:
|r|>0.75 – сильний0.5<|r|<0.75 середній
|r|<0.5 -слабкий
r<0 – негативна
кореляція,
r>0 – позитивна
кореляція
6.
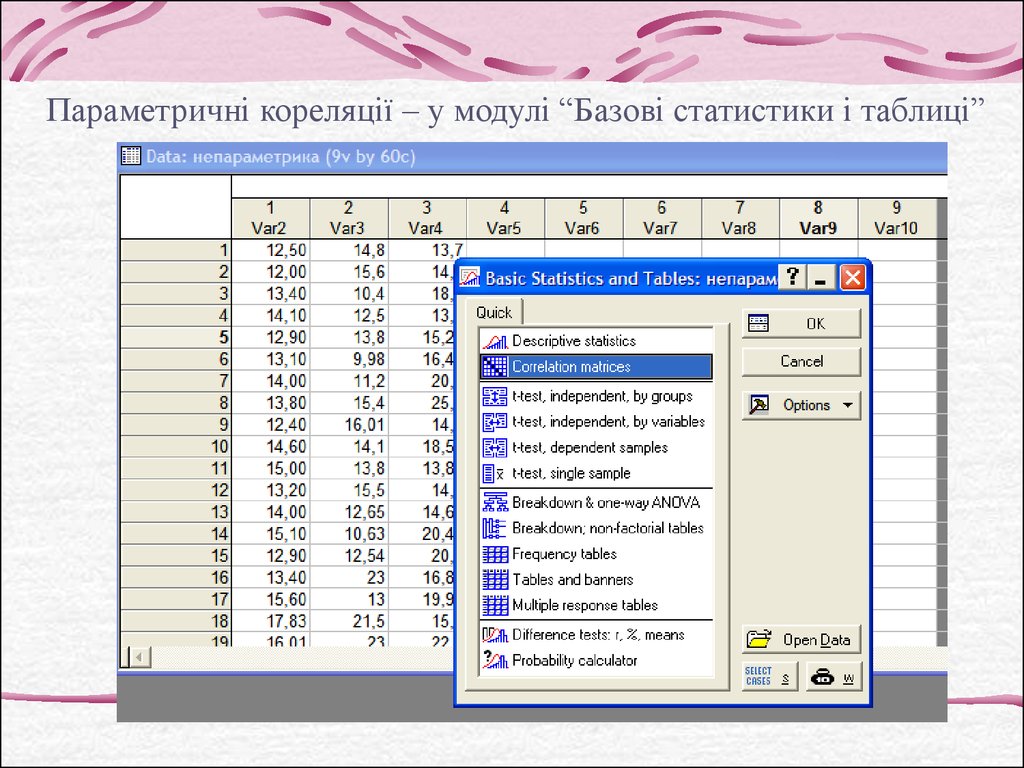
Параметричні кореляції – у модулі “Базові статистики і таблиці”7.
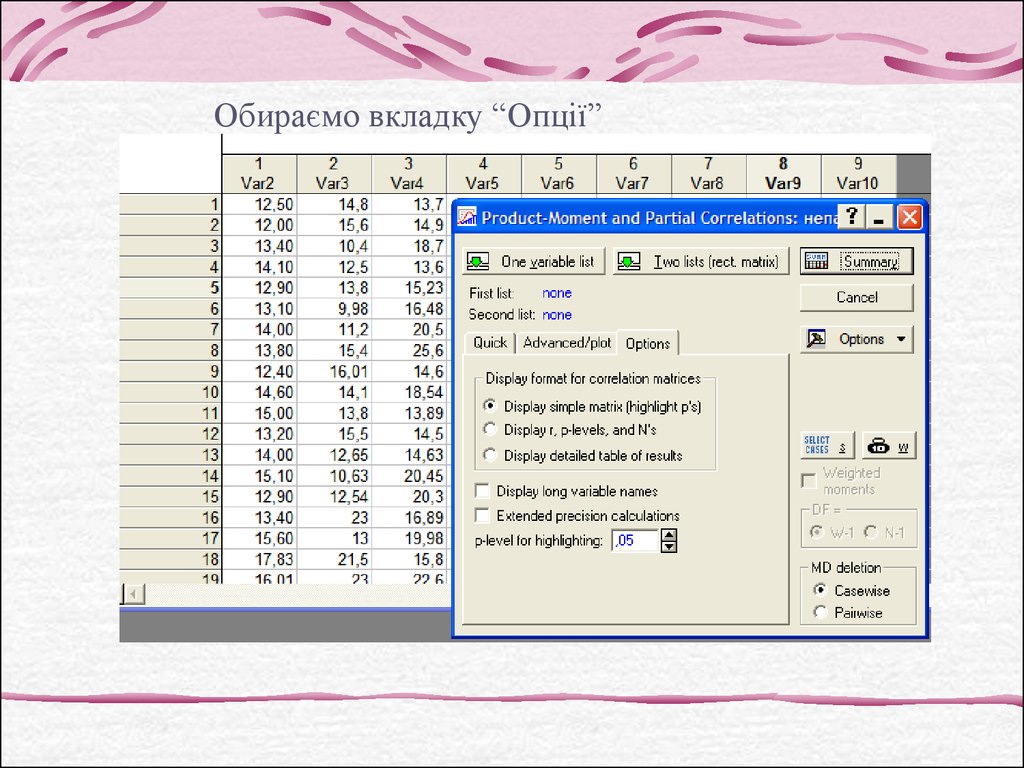
Обираємо вкладку “Опції”8.
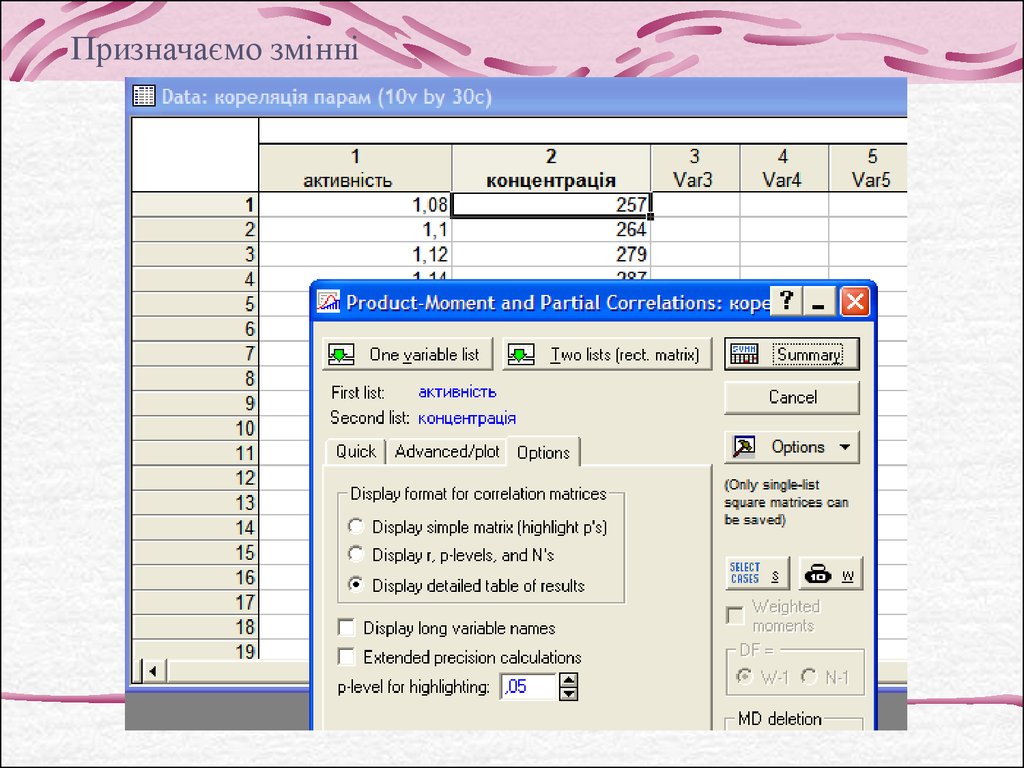
Призначаємо змінні9.
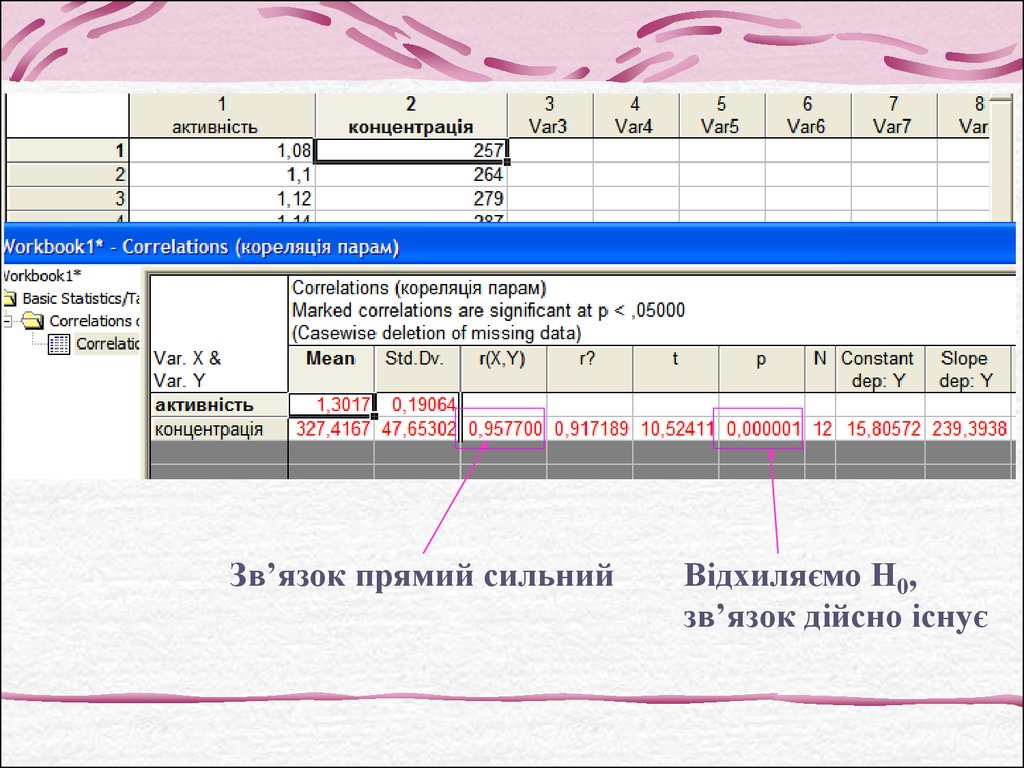
Зв’язок прямий сильнийВідхиляємо Н0,
зв’язок дійсно існує
10. Cтатистична похибка коефіцієнта кореляції та довірчий інтервал:
Вибірковий коефіцієнт rхарактеризує генеральний
параметр ρ зі статистичною
похибкою:
Довірчий інтервал
коефіцієнта кореляції:
r t sr r t sr
1 r 2
sr
n 2
Статистична значущість
коефіцієнта r:
Н0: зв’язок між х і у відсутній,
ρ=0
Перевіряють за критерієм
Стьюдента:
r
t
sr
Табличне значення:
tтабл (α, n-2)
При tтабл > t, приймають Н0
11. Коефіцієнт кореляції для малих вибірок:
Для вибірок з n<30 вводятьпоправку:
1 r 2
r* r 1
2
(
n
3
)
Для малочисельних вибірок,
коли r<=0.2 або r>0.5
використовують
перетворення Фішера, r
замінюють на z:
1 1 r
z ln
2 1 r
Похибка z:
Критерій значущості z:
z
z n 3
sz
Табличне значення: tтабл(α, n-2)
При tтабл > t, приймають Н0
t
sz
1
n 3
12. Статистична значущість різниці коефіцієнтів кореляції
Н0: вибірки взяті з одноїгенеральної сукупності або з
генеральних сукупностей з
однаковим типом зв’язку між
показниками
Для великих вибірок n>100:
t
r1 r2
s s
2
r1
2
r2
tтабл (α, n1+n2-4)
При t<tтабл приймаємо Н0
Коли n<100 і r>0.5,
порівнюють коефіцієнти
кореляції після перетворення в
z:
z z
t
1
2
1
1
n1 3 n2 3
tтабл (α, n1+n2-4)
При t<tтабл приймаємо Н0
13. 2. Непараметричний кореляційний аналіз (коефіцієнти кореляції рангів)
Застосовують: безпередбачення про характер
розподілу
Коефіцієнт кореляції
рангів Спірмена:
rs 1
6
n( n 2
(R
1)
x
Ry ) 2
Rx, Ry – різниця між рангами
спряжених значень ознак х і у
(коли значення у вибірці
співпадають, ранги
усереднюються)
0<r <1
s
Значущість коефіцієнта rs
перевіряють за критерієм
Стьюдента:
n 2
t | rs |
2
1 rs
Н0: зв’язок між х і у відсутній,
ρ=0
tтабл (α, n - 2)
При t<tтабл приймаємо Н0
14.
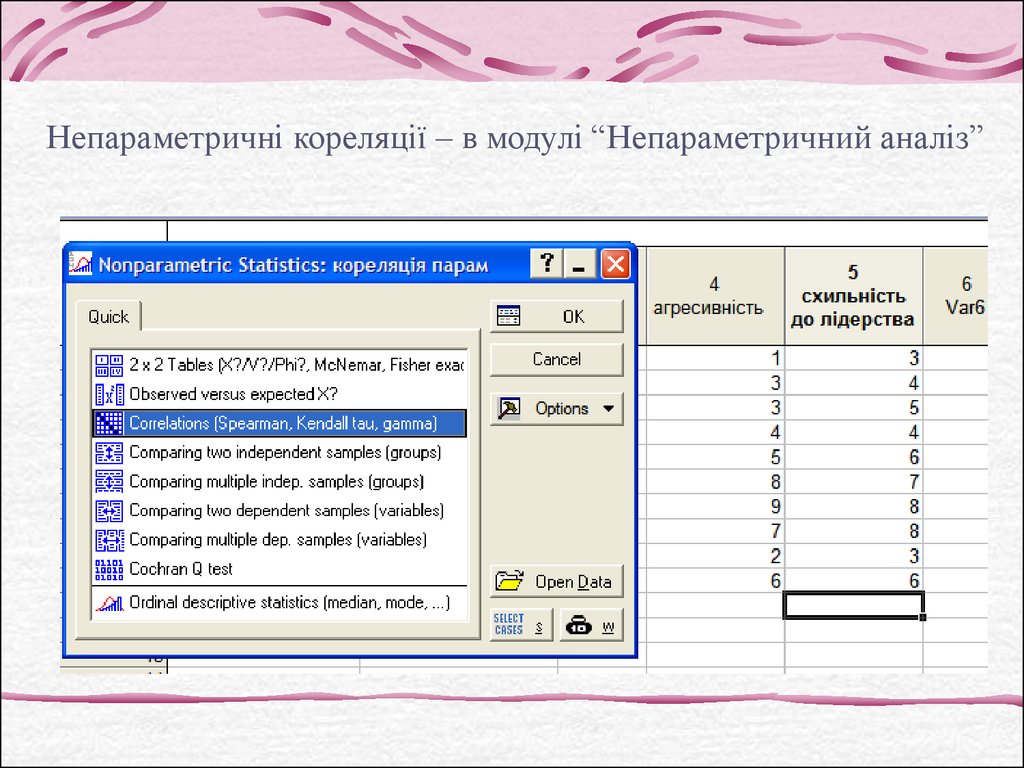
Непараметричні кореляції – в модулі “Непараметричний аналіз”15.
16.
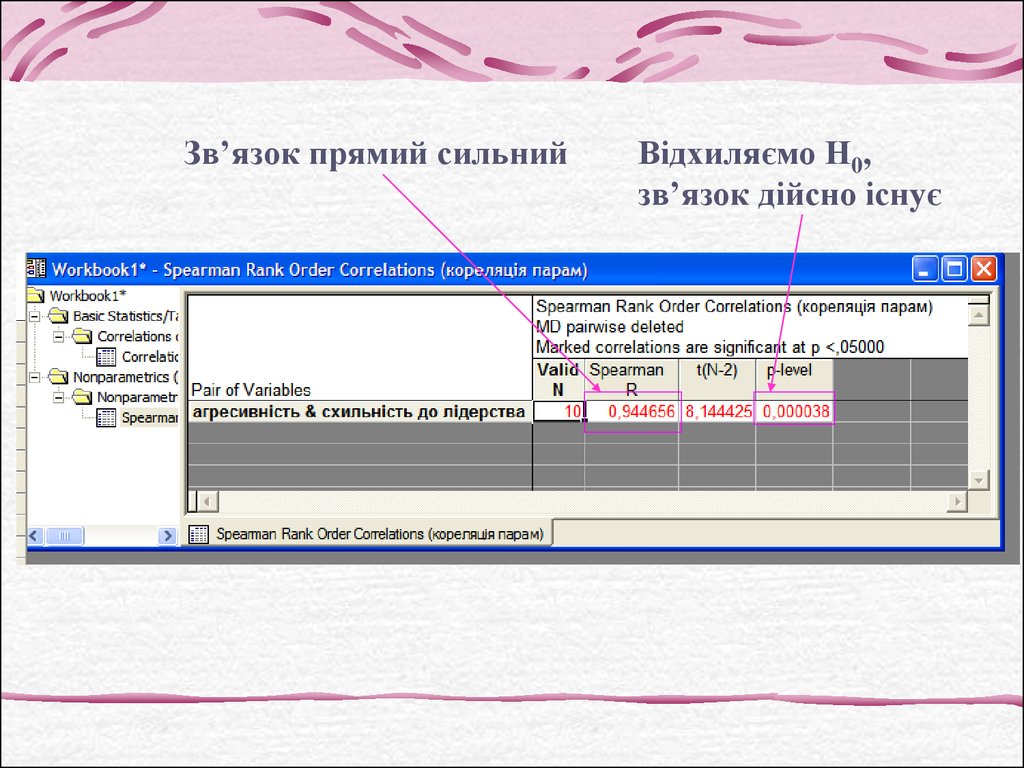
Зв’язок прямий сильнийВідхиляємо Н0,
зв’язок дійсно існує
17. Cила зв’язку:
r2=0.25-0.75 –середній,
r2<0.25 – слабкий,
r2>0.75 - сильний
Коефіцієнт
детермінації r2
Показує, яка частина
варіації одної ознаки
залежить від
варіювання іншої
ознаки.
Розраховується як r2
18. Зв’язок між якісними ознаками: таблиці 2х2; коефіцієнт асоціації Пірсона rA
Маємо кореляційну таблицю даних:Ознака Ознаки
є
немає
Група1
Група2
Суми:
Суми:
а
b
a+b
c
d
c+d
a+c
b+d
Тут а, b, c і d – кількість випадків
ad bc
rA
(a b)(c d )( a c)(b d )
Похибка:
1 rA2
srA
n
Критерій перевірки значущості:
2 n * rA2
2 табл ( ;1);
при 2 2 табл відхиляють Н о
і говорять про значущість rA
19. Бісеріальний коефіцієнт кореляції rBS
Використовують, коли однаознака бінарна (наприклад,
стать), а інша кількісна:
rBS
x1 x2
n1n2
N ( N 1)
Тут 1 і 2 – коди бінарної ознаки,
Х1 – середня по кількісній
ознаці, яка належить до 1
групи (код бінарної ознаки
1),
Х2 – аналогічно для 2 групи,
σ – стандартне відхилення
кількісної ознаки
Критерій значущості:
t rBS
N 2
2
1 r BS
Табличне значення:
tтабл (α;N-2)
При t> tтабл відхиляють Но і
говорять про наявність зв’язку
20. Регресійний аналіз
Регресійний аналіз – це методистатистичного аналізу, які
встановлюють як кількісно
змінюється одна ознака при зміні
іншої
Регресійна залежність : y=f(x), де
х – незалежна змінна, у – залежна
змінна; коли маємо декілька
незалежних змінних х1, х2, ... –
проводять багатофакторний
(множинний) регресійний аналіз
Регресія – це зміна функції (у) при
зміні одного чи декількох аргументів
(х)
Задача застосування в
біології:
спрогнозувати
(розрахувати) значення
залежної ознаки за
певним значенням
незалежної ознаки:
наприклад, спрогнозувати
тривалість гострої фази
захворювання залежно від
температури і титру
антитіл в крові пацієнтів
21.
Умови застосування регресійного аналізу:Кількість об’єктів дослідження має бути в декілька разів більше,
ніж кількість незалежних ознак,
Усі ознаки повинні бути кількісними і нормально
розподіленими
Залежна ознака У повинна мати нормальний розподіл з
однаковими дисперсіями для кожного значення незалежної
ознаки Хі (для багатофакторного аналізу)
У випадку багатофакторного аналізу не повинні існувати сильні
лінійні зв’язки між незалежними ознаками, коли це так – в
модель включають ознаку Х, яка має найбільший коефіцієнт r з
залежною ознакою У
Різниця між теоретичним і реальним значеннями Δу повинна
бути нормально розподіленою і мати нульове значення
середнього,
22. Лінійна регресія
Рівняння зв’язку між х та у маєвигляд: y a bx або
y a b1 x1 b2 x2 ...
Тоді коефіцієнти а і b
розраховують як:
y
byx r
x
tgα = b
α
а
a y bx
Тут а – вільний член (intercept) , b – коефіцієнт регресії (slope)
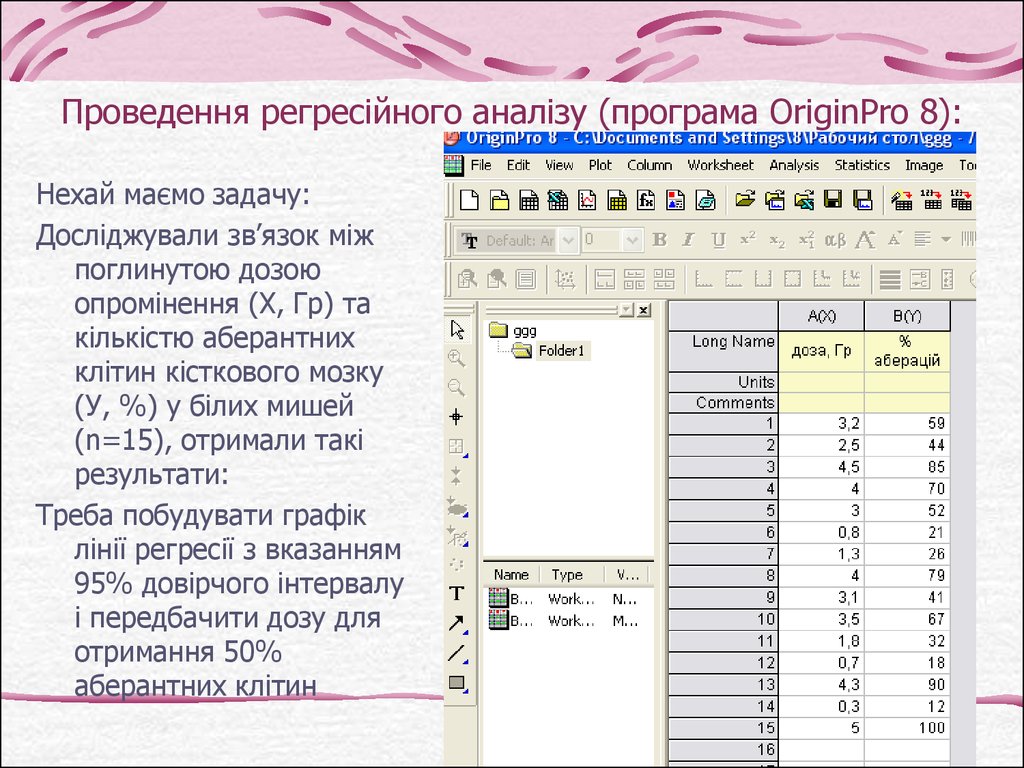
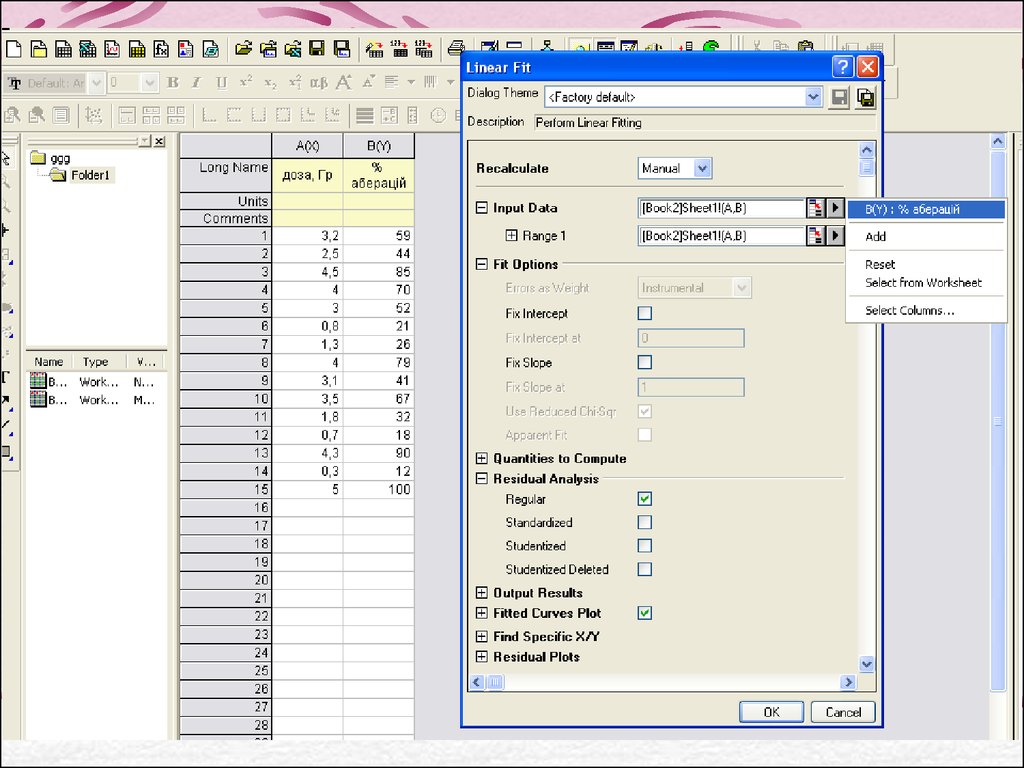
23. Проведення регресійного аналізу (програма OriginPro 8):
Нехай маємо задачу:Досліджували зв’язок між
поглинутою дозою
опромінення (Х, Гр) та
кількістю аберантних
клітин кісткового мозку
(У, %) у білих мишей
(n=15), отримали такі
результати:
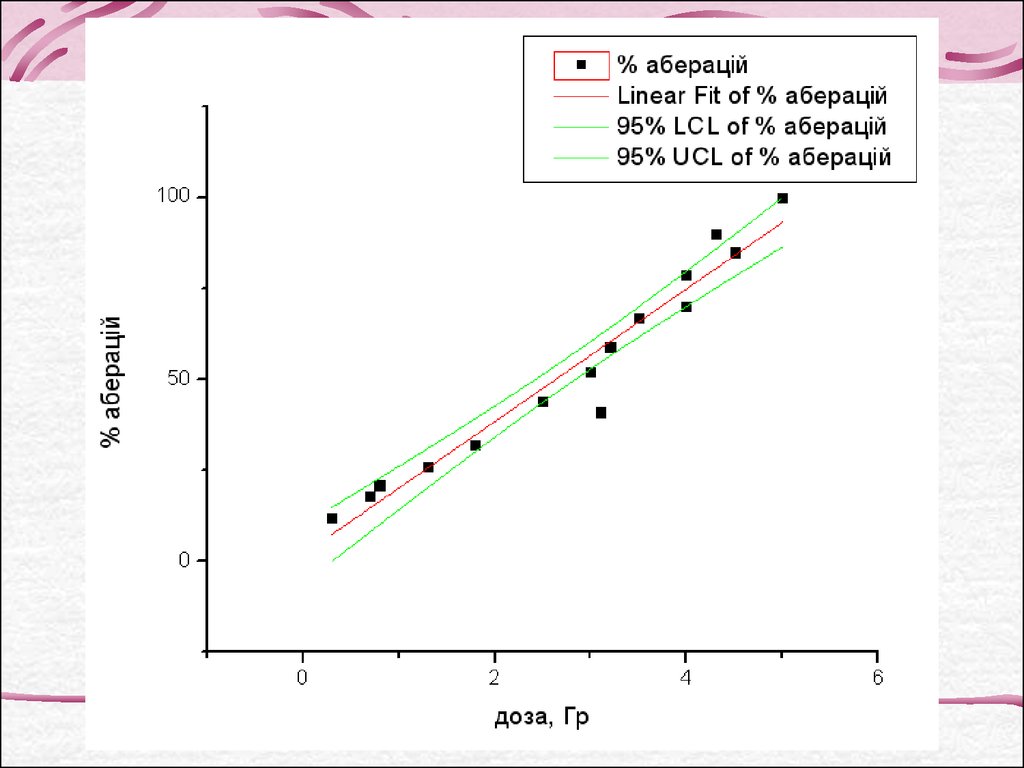
Треба побудувати графік
лінії регресії з вказанням
95% довірчого інтервалу
і передбачити дозу для
отримання 50%
аберантних клітин
24.
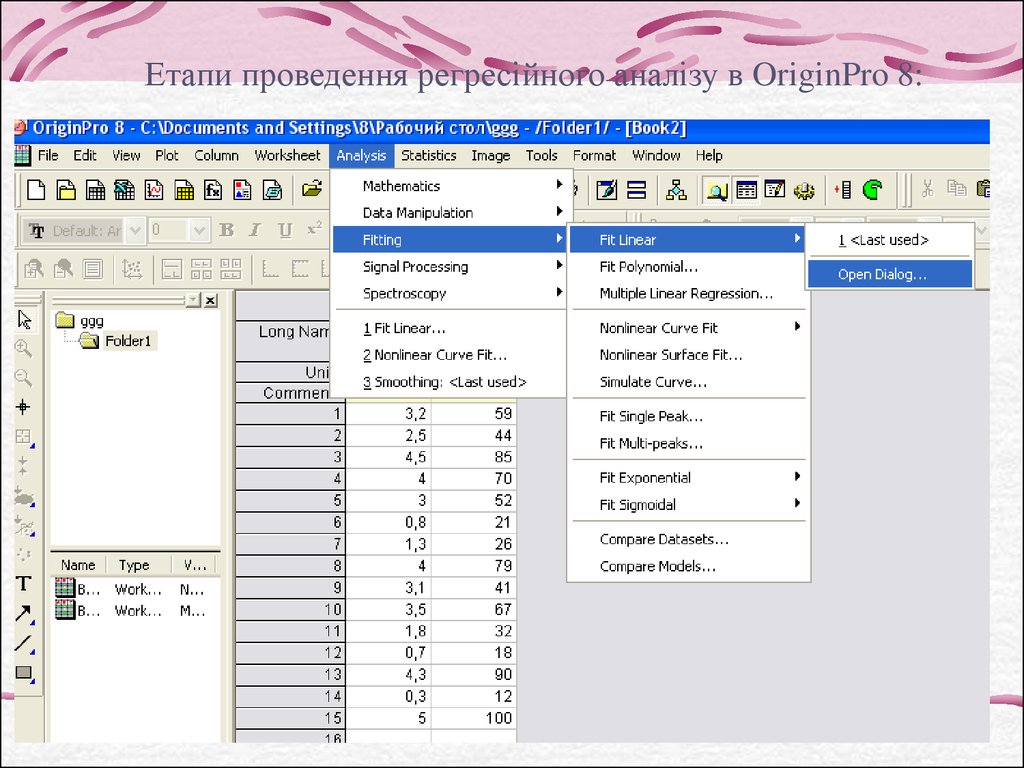
Етапи проведення регресійного аналізу в OriginPro 8:25.
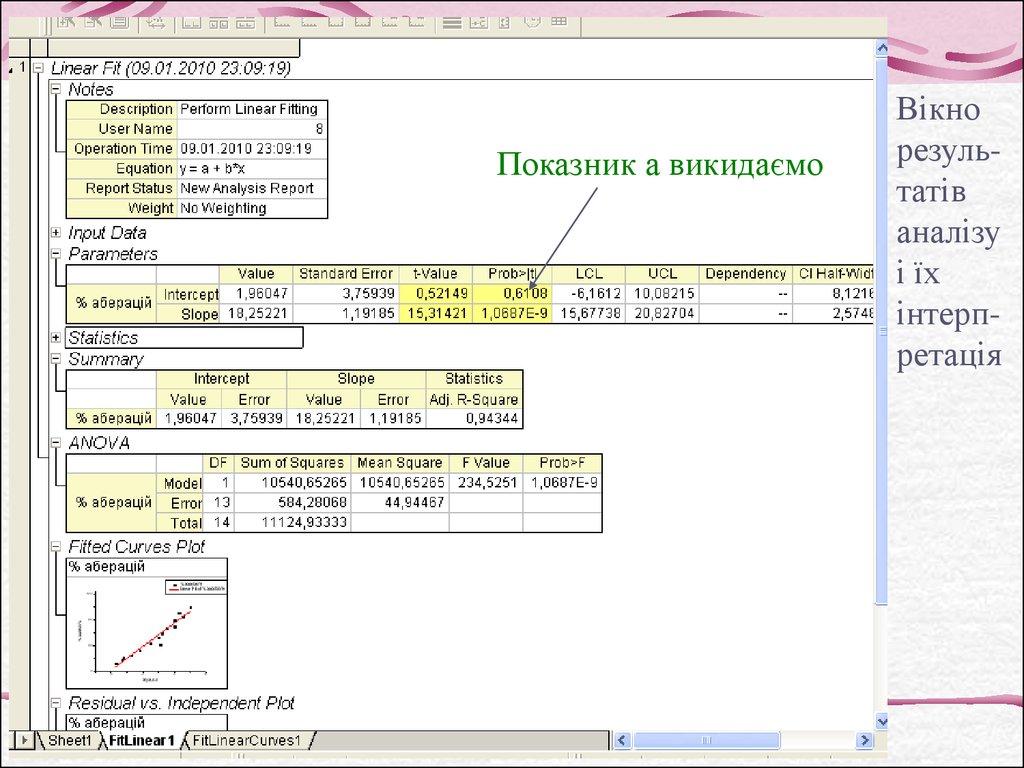
26.
Показник а викидаємоВікно
результатів
аналізу
і їх
інтерпретація
27. Довірчий інтервал
Для оцінювання похибкипри прогнозуванні
параметра У по Х
використовують довірчий
інтервал:
yk yk t0.95 m yk
Тут уk – прогнозоване
значення параметра у при
значення незалежного
фактора хі,
Похибка оцінювання:
m y k so
( xk x ) 2
1
n xi2 nx 2
Тут so – середнє
квадратичне відхилення
параметра У,
Хk – значення фактора х,
одержаного з рівняння
28.
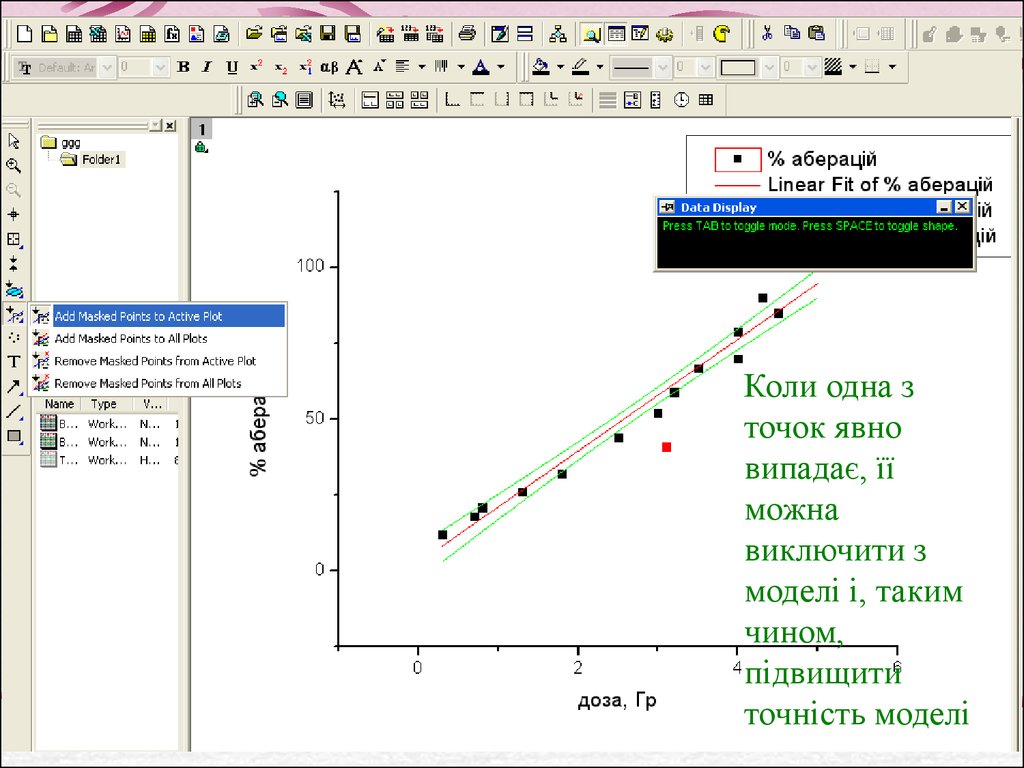
29.
Коли одна зточок явно
випадає, її
можна
виключити з
моделі і, таким
чином,
підвищити
точність моделі
30.
Для цього ми спочатку згрупи інструментів
Regional Mask Tool
вибираємо команду Add
Mask Points to Active
Plot,
Потім виділити за
допомогою мишки
прямокутну область
навколо точки – точка
забарвиться в червоний
колір,
І знову провести
кореляційний аналіз:
Analysis – Fitting – Fit
Linear – Last Used
Виділена точка не буде
врахована, а точність
коефіцієнтів і в цілому
моделювання – зросте
Усе рівно, показник
а викидаємо
31. Дисперсійний аналіз – засіб перевірки значущості моделі:
Наслідком дисперсійногоаналізу є розрахунок
коефіцієнта детермінації R2:
SS R
R
SS
2
Тут SSR – сума квадратів
відхилень розрахованих
значень уі від середнього у, а
SS – сума квадратів відхилень
експериментальних значень уі
від середнього у.
Коефіцієнт детермінації
напряму пов’язаний зі
значенням F-критерію:
DR2
F 2
D0
Тут DR2 – дисперсія відхилень
розрахункових значень уі від
середнього у, і D02 – дисперсія
відхилень експериментальних
значень уі від середнього у.
32.
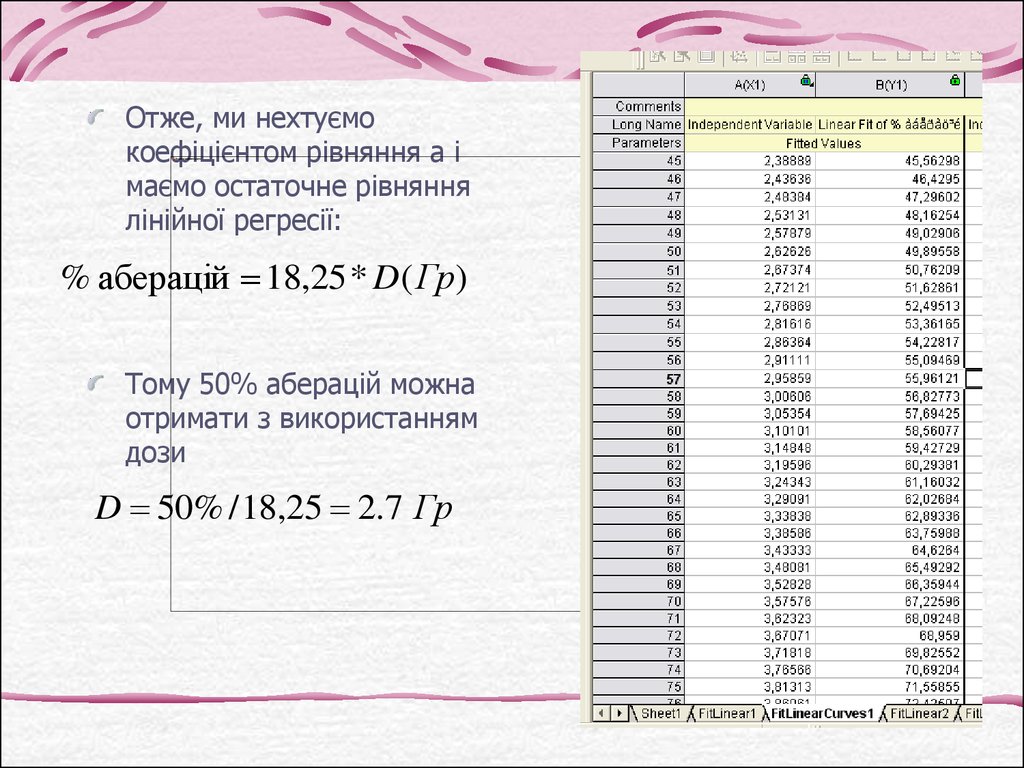
Отже, ми нехтуємокоефіцієнтом рівняння а і
маємо остаточне рівняння
лінійної регресії:
% аберацій 18,25 * D( Гр)
Тому 50% аберацій можна
отримати з використанням
дози
D 50% / 18,25 2.7 Гр
33. Інтерпретація результатів:
Коли для моделі р<0,05 –регресійна модель адекватно
описує взаємозв’язок між У та Х,
Коефіцієнт детермінації r2 вказує,
яка частина варіація У
визначається варіацією Х, коли
r2>0.5 – модель є значущою на
рівні Р=0,95
Ваговий коефіцієнт b показує,
наскільки змінюється показник У
при одиничній зміні Х.
У випадку, коли для коефіцієнтів
а або b р>0,05 – цим
коефіцієнтом нехтують як
незначущим
Застосування результатів
аналізу з прогностичною
метою можливо тільки для
того діапазону даних, на
якому вони були отримані
34. Нелінійний регресійний аналіз
Найбільш часто зустрічаютьсяу біології такі нелінійні
залежності:
Експоненційна
y e a bx
Ступенева
y a x
b
Зворотна
b
y a
x
Найпростіший спосіб аналізу
таких даних – лінеаризація,
зокрема, логарифмуванням:
ln y a b x, приймемо Z ln y
ln y ln a b ln x, приймаємо ln y Z ,
b0 ln a, t ln x
Z b0 b t
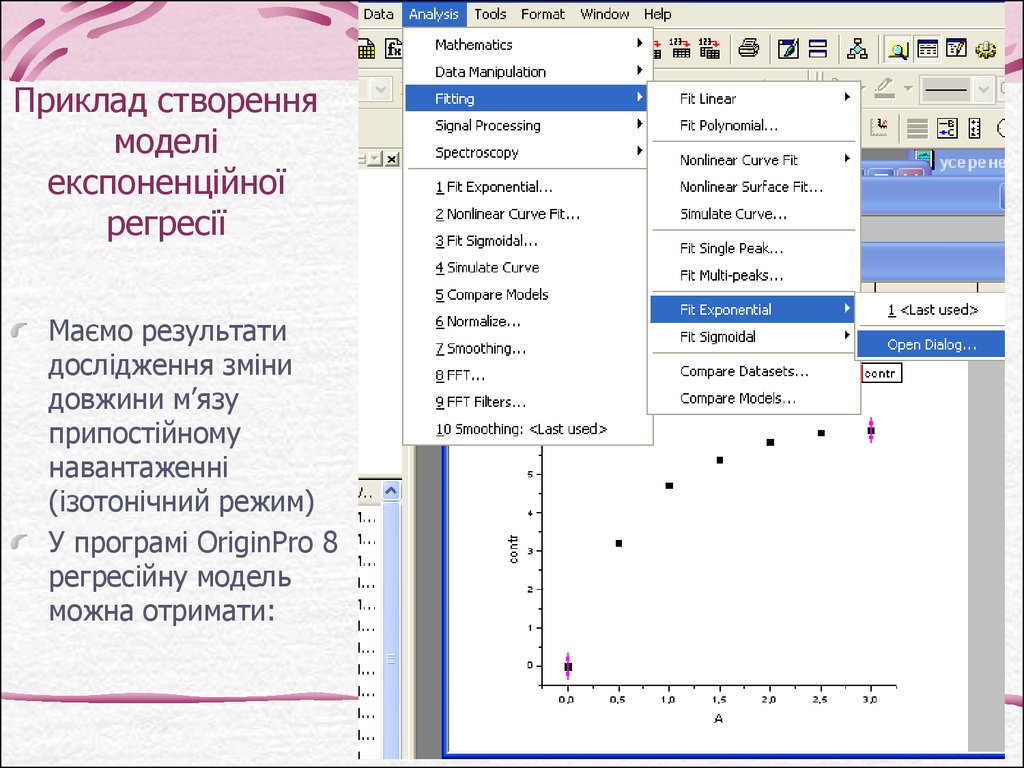
35. Приклад створення моделі експоненційної регресії
Маємо результатидослідження зміни
довжини м’язу
припостійному
навантаженні
(ізотонічний режим)
У програмі OriginPro 8
регресійну модель
можна отримати:
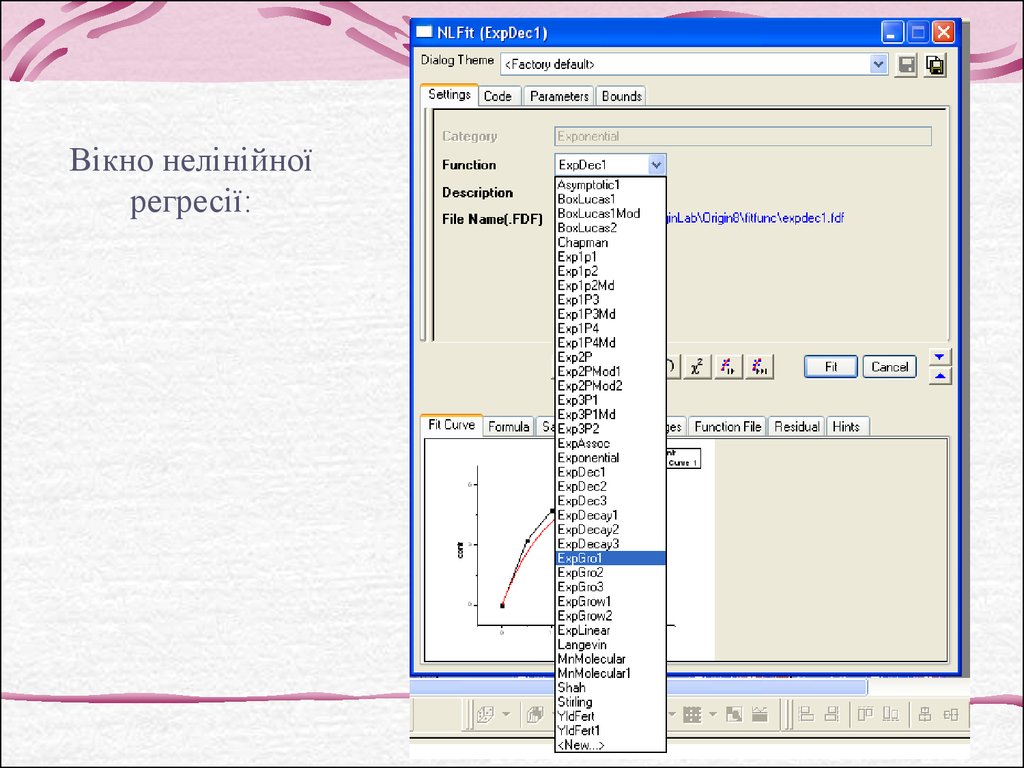
36.
Вікно нелінійноїрегресії:





















 mathematics
mathematics








