Класична лінійна багатофакторна модель

1. Лекція 3

Класична лінійна
багатофакторна модель.
Кафедра інформаційних технологій
доцент Бесклінська О.П.
1

2.

Зміст:
1. Методи побудови багатофакторної
регресійної моделі
2. Етапи дослідження загальної
лінійної моделі множинної регресії
3. Приклад параметризації та
дослідження багатофакторної
регресійної моделі
2

3.

1. Методи побудови багатофакторної
регресійної моделі
1
2
3
Метод усіх можливих регресій
Метод виключень
Покроковий регресійний метод
3

4. 2. Етапи дослідження загальної лінійної моделі множинної регресії

Розглядається багатофакторна лінійна регресійна
модель
y a0 a1 x1 a2 x2 ... am xm
4

5.

Для дослідження моделі слід виконати такі
кроки.
11. За даними спостережень оцінити параметри а1 , а2 ,..., ат
22. Для перевірки адекватності отриманої моделі обчислити:
а) залишки моделі — розбіжності між спостереженими
та розрахунковими значеннями
залежної змінної ui yi yˆ i , і = 1, 2,..., п
б) відносну похибку залишків та її середнє значення
5

6.

в) залишкову дисперсію
г) коефіцієнт детермінації
д) вибірковий коефіцієнт множинної
кореляції
6

7.

33.
Перевірити статистичну значущість
отриманих результатів:
а) перевірити адекватність моделі загалом:
за допомогою F-критерію Фішера перевірити гіпотезу
Н0 :
a1 a2 ... am 0
проти альтернативної
НА: існує хоча б один коефіцієнт
aj 0
7

8.

б) перевірити значущість коефіцієнта
множинної кореляції, тобто розглянути гіпотезу
Н0 : R = 0
в) перевірити істотність коефіцієнтів регресії:
за допомогою t-критерію Стьюдента
перевірити гіпотезу
Н0 : a j 0 для всіх j = 1, 2,..., т
проти відповідних альтернативних гіпотез
НА : a j 0 для всіх j = 1, 2,..., т;
8

9.

44. Обчислити та інтерпретувати
коефіцієнти еластичності
55. Визначити довірчі інтервали регресії
при рівні значущості α.
66. Побудувати довірчі інтервали
для параметрів регресії.
9

10.

77. Обчислити прогнозні значення ур
за значеннями x1 p , x 2 p ,..., x mp ,
що перебувають за межами
базового періоду,
і знайти межі довірчих інтервалів
індивідуальних прогнозованих значень
і межі довірчих інтервалів
середнього прогнозу.
10

11. 3. Приклад параметризації та дослідження багатофакторної регресійної моделі

11

12.

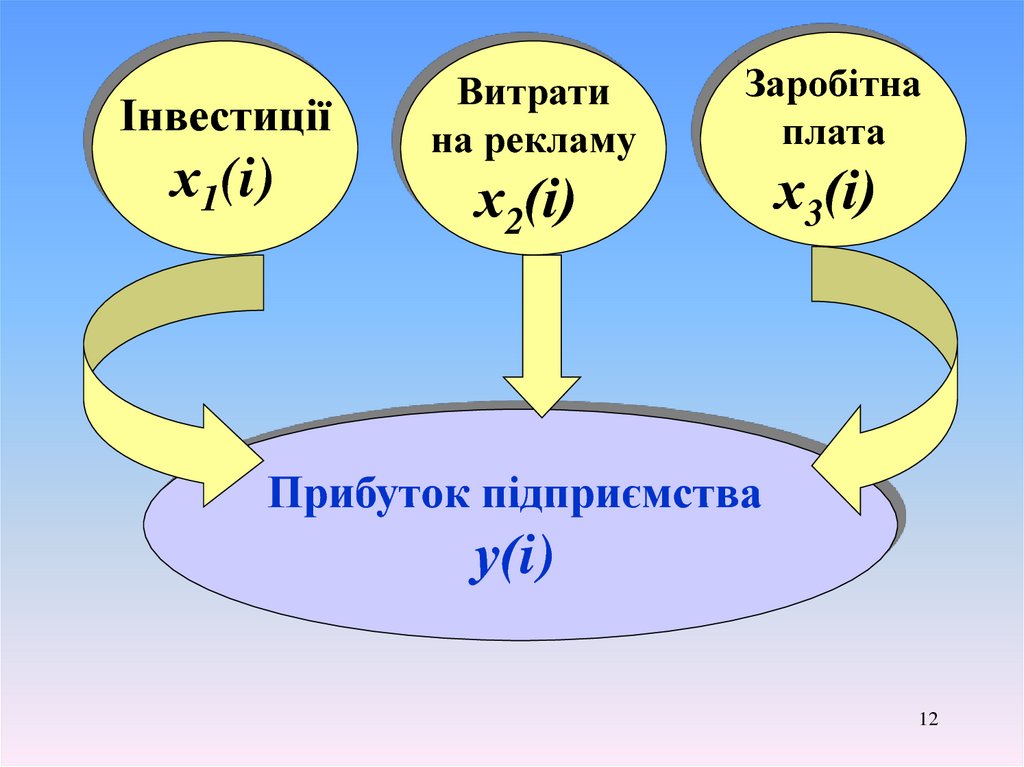
Інвестиції
х1(i)
Витрати
на рекламу
Заробітна
плата
х2(і)
х3(і)
Прибуток підприємства
у(i)
12

13.

Припустимо, що між економічним
показником у і факторами х1 , х2 , х3
існує лінійний зв'язок.
y a0 a1 x1 a2 x2 a3 x3
a0 , a1 , a2 , a3
параметри моделі, які потрібно оцінити
13

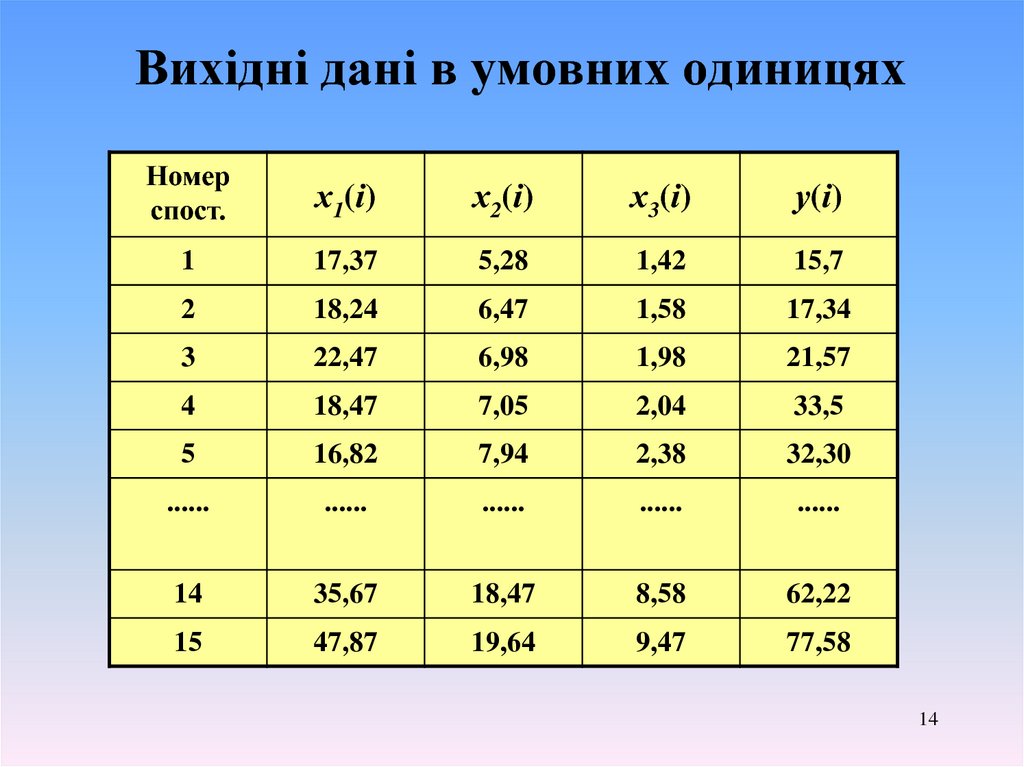
14. Вихідні дані в умовних одиницях

Номер
спост.
х1(і)
х2(і)
х3(і)
у(і)
1
17,37
5,28
1,42
15,7
2
18,24
6,47
1,58
17,34
3
22,47
6,98
1,98
21,57
4
18,47
7,05
2,04
33,5
5
16,82
7,94
2,38
32,30
......
......
......
......
......
14
35,67
18,47
8,58
62,22
15
47,87
19,64
9,47
77,58
14

15. Знайдемо МНК-оцінки параметрів моделі.

1
Знайдемо МНК-оцінки параметрів
моделі.
х1(і) х2(і) х3(і)
15

16. Обчислимо оцінки регресійних коефіцієнтів за формулою

T
1
T
a (X X ) X Y
де XT — транспонована матриця X
16

17.

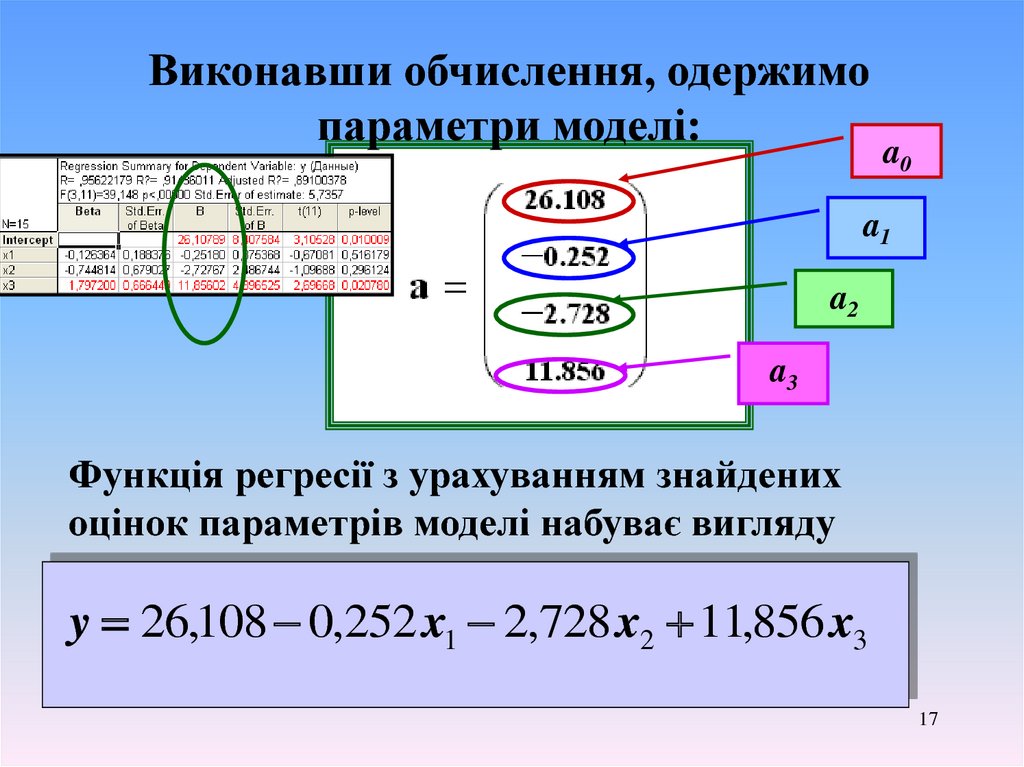
Виконавши обчислення, одержимо
параметри моделі:
a0
a1
a2
a3
Функція регресії з урахуванням знайдених
оцінок параметрів моделі набуває вигляду
y 26,108 0,252 x1 2,728 x2 11,856 x3
17

18.

2
Для перевірки адекватності отриманої моделі
обчислимо:
а) Залишки u y y
i
i
i
б) Відносну похибку розрахункових значень
регресії:
u
i
i
yi
100%
середнє значення відносної похибки
n
i 1
n
i
У нас
0,52783
18

19.

в)
Обчислимо
середньоквадратичну
помилку дисперсії збурень
n
Sˆ u ˆ u
У нас
u
i 1
2
i
n m 1
ˆ
Su 5,7357
19

20.

г) Перевіримо тісноту загального зв'язку (впливу)
незалежних змінних на залежну змінну.
Для
цього треба обчислити коефіцієнт детермінації за
формулою
n
R2 1
2
u
i
i 1
n
2
(
y
y
)
i
i 1
У нас
R 0,91436
2
Висновок: чим ближчий він до одиниці, тим більше варіація
залежної змінної y визначається варіацією незалежної
змінної x
20
(є тісний зв'язок між залежною та незалежними змінними).

21.

д) Перевіримо на значущість вибірковий
коефіцієнт кореляції.
Для цього обчислимо R R 2 - коефіцієнт
кореляції (характеризує тісноту лінійного
зв'язку всіх незалежних факторів xi із
залежною змінною y).
У нас
R R 2 0,91436 0,956222
21

22.

3
Перевіримо статистичну
значущість отриманих результатів
.
а) Обчислимо F-статистику за формулою
Fексп
R2 n m 1
2
1 R
m
Знайти табличне значення: F (m, n m 1, )
і порівняти його з обчисленою F – статистикою: якщо
Fексп F (m, n m 1, )
то гіпотеза відхиляється, інакше приймається.
22

23.

У нас
Маємо Fексп=39,14827,
табличне значення: F ( 3; 11; 0 ,05 ) 3,59
Порівняємо його з обчисленою
Оскільки F F ( 3;11;0 ,05 )
експ
F-статистикою.
нульова гіпотеза відхиляється, тобто коефіцієнти
регресії є значущими.
23

24.

б) Обчислимо t-статистику за формулою
t
Якщо
R n m 1
1 R
2
t t табл ( / 2, n m 1)
t табл ( / 2, n m 1)
де
відповідне табличне значення t-розподілу з
(n-m-1) ступенями свободи, то можна зробити
висновок про значущість коефіцієнта кореляції
між залежною і незалежними змінними моделі.
24

25.

У нас
Маємо t = 37,03215.
Відповідне табличне значення
tтабл (0,025; 11) 2,593097
Оскільки
t tтабл (0,025; 11)
можна зробити висновок про достовірність
коефіцієнта кореляції, який характеризує тісноту
зв'язку між залежною та незалежними змінними
моделі.
25

26.

Для вибраного рівня значущості і
відповідного ступеня вільності k=n-т-1
записати межі надійності для множинного
коефіцієнта кореляції R:
(R- R; R+ R), де
1 R
R t / 2,k
n
26

27.

У нас
Маємо
1 0,956222
R 2,593
0,029311
15
отже
( R R ; R R) (0,926911 ; 0,985533)
27

28.

в) Перевіримо значущість
коефіцієнтів регресії.
окремих
Визначимо t-статистику за формулою
tj
де
c jj
aj
u2c jj
aj
Sa j
- діагональний елемент матриці
( X T X ) 1
,
Sa j
- стандартизована помилка оцінки
параметра моделі.
28

29.

Значення tj-критерію порівнюється з
табличними при k = n-m-1 ступенях
свободи і рівні значущості :
якщо |tj| >t /2,k , то відповідна оцінка
параметра регресійної моделі є значуща;
інакше приймаємо гіпотезу про рівність
aj нулю
29

30.

У нас
t 0 3,105278; t1 0,67081;
t 2 1,09688; t3 2,696681
tтабл (0,025,11) 2,593097
табличне значення
Оскільки t0 t / 2,k ; t1 t / 2,k ; t2 t / 2,k ; t3 t / 2,k
відповідно оцінки
а оцінки
aˆ1 , aˆ 2
aˆ 0 , aˆ3 є значущими
не є значущими
30

31.

Обчислимо коефіцієнти еластичності
за формулою
4
y xi
i
.
x i y
коефіцієнт еластичності є показником впливу
зміни питомої ваги xi на y у припущенні, що
вплив інших факторів відсутній: показує, що
регресанд y зміниться на %, якщо фактор x
зміниться на 1%
31

32.

y 26 ,108 0 ,252 x1 2,728 x2 11,856 x3
y
0 ,252
x1
x1 23,416
y 43,08
y x1
23,416
1
0 ,252
0 ,137
x1 y
43,08
32

33.

У нас
α1= -0,137; α2 = -0,699; α3 = 1,24
У нашому випадку він показує, що прибуток
підприємства зменшиться на 0,14 %, якщо
інвестиції зростуть на 1%, прибуток
підприємства зменшиться на 0,7 %, якщо
витрати на рекламу зростуть на 1 %, прибуток
підприємства збільшиться на 1,24 %, якщо
заробітна плата зросте на 1 %.
33

34.

Загальна еластичність Y від усіх
факторів хi дорівнює:
m
i
i 1
Цей показник свідчить, що на %
зміниться y , якщо одночасно
збільшити на 1% всі фактори xi)
У нас
α=0,394033.
34

35.

Обчислимо довірчі інтервали для
математичного сподівання ŷ
і для кожного спостереження
5
X i (1, x1(i ) , x2(i ) , x3(i ) )
T
yˆ i yˆ i ; yˆ i yˆ i ,
де
T
T
1
ˆ
yˆ i t / 2,k S u X i ( X X ) X i
35

36.

де Ŝu — незміщена оцінка дисперсії
залишків:
У нас
Sˆ u 5,7357
Виконавши необхідні розрахунки, отримаємо
довірчі зони регресії:
(23,430; 24,904)
(22,594; 22,604)
(24,730; 25,041)
..........................
(62,887; 63,558)
(68,229; 68,712)
(71,961;73,556)
36

37.

6
Побудуємо довірчі інтервали для
параметрів регресії.
(a j t / 2,k c jj ; a j t / 2,k c jj )
2
u
2
u
Довірчий інтервал при рівні надійності (1- ) є
інтервал з випадково залежними межами і
накриває істинне значення коефіцієнта
регресії aj з рівнем довіри (1- ).
c jj
діагональний елемент матриці
( X T X ) 1
37

38.

У нас
Стандартні похибки
c jj
2
u
a0 (7,85; 44,47)
a2 ( 8,126; 2,801)
tтабл (0,025;11) 2,20
a1 ( 1,095; 0,539)
a3 (2,195; 21,44)
38

39.

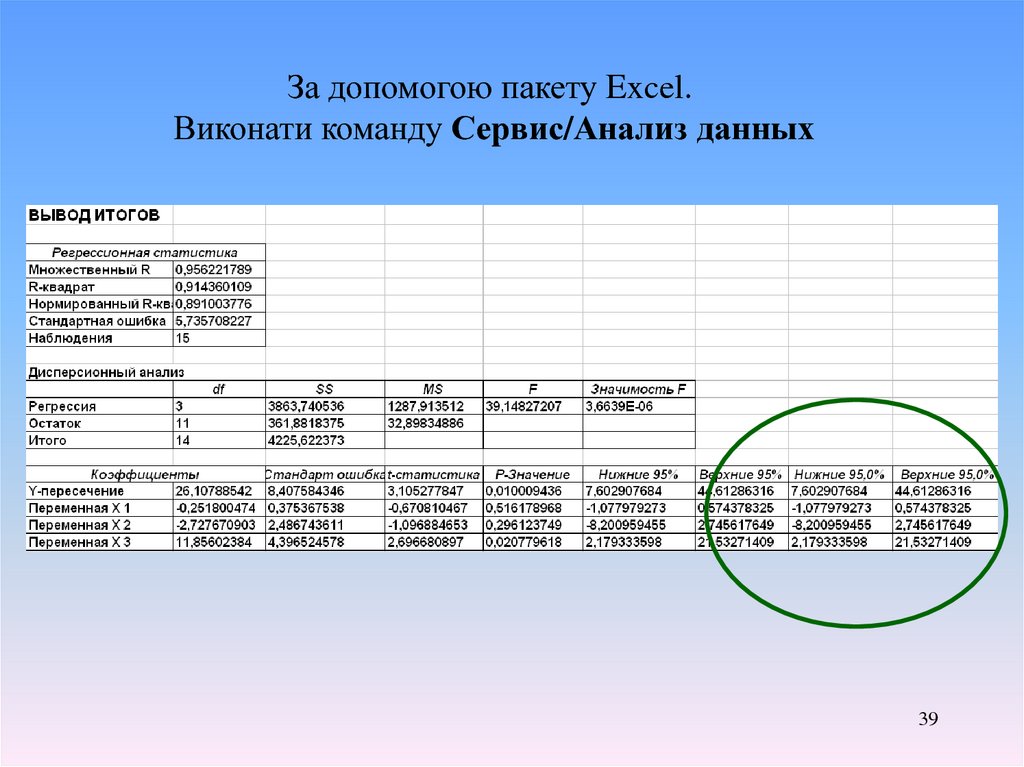
За допомогою пакету Excel.
Виконати команду Сервис/Анализ данных
39

40.

7
Обчислимо прогнозні значення і знайдемо
межі довірчих інтервалів індивідуальних
прогнозних значень і межі довірчих
інтервалів для математичного сподівання
(точковий та інтервальний прогнози).
40

41.

а) для обчислення прогнозних
y pi Yпрзначень
у рівняння
yˆ aˆ0 aˆ1 x1 aˆ2 x2 aˆ3 x3
тобто
yˆ 26,108 0,252 x1 2,728x2 11,856 x3
підставимо задані значення
x pi
41

42.

У нас
Підставимо
x1пр 48,82,
x 2 пр 20,04,
x3пр 10,25
одержимо
y пр 80,68
42

43.

б) знайдемо межі довірчих інтервалів
індивідуальних прогнозованих значень за
формулою:
Yˆпр Yˆпр Yпр Yˆпр Yˆпр ,
де
T
T
1
ˆ
Yпр t / 2 ˆ u 1 X пр ( X X ) X пр
43

44.

У нас
Yˆпр 80,68
u 5,7357
X пр 48,82; 20,04; 10,25
тоді
Yпр (58,72; 102,64)
інтервальний прогноз індивідуального значення
44

45.

в) знайдемо межі довірчих інтервалів для
математичного сподівання значення ypi за
формулою:
Yˆпр 1 M (Yпр ) Yˆпр 1,
де
1 t / 2 ˆ u X ( X X ) X пр
T
пр
T
1
45

46.

У нас
Yˆпр 80,68
u 5,7357
тоді
M (Yпр ) (64,52; 96,83)
довірчий інтервал для математичного сподівання.
46

47. Завдання для самостійної роботи

Лугінін О.Є. Економетрія.
Стор.123-132.
Приклад 6.3 розібрати
розв‘язок.
?
47

48. Експрес контроль

Знайти значення критерію Фішера
для парної регресії, якщо n=10+k,
R2=0,9t,
де k- номер по списку,
t- номер групи (1,2,3,4,5,6,7)
48