Similar presentations:
Однофакторні нелінійні економетричні моделі
1. ОДНОФАКТОРНІ НЕЛІНІЙНІ ЕКОНОМЕТРИЧНІ МОДЕЛІ
2. План
1. Криві зростання2. Зведення нелінійних моделей до
лінійних:
2.1.
Лінеаризація квадратичних функцій
2.2.
Лінеаризація зворотних кривих
зростання
2.3.
Лінеаризація експоненційних
функцій
2.4. Лінеаризація степеневих функцій
3. 1. Криві зростання
експоненційнастепенева
зворотна
квадратична
модифікована
експоненційна
крива Гомперця
логістична крива
y x
y x
1
y
x
2
y x x
y
x
y e
y
x
1
x
4. 2. Зведення нелінійних моделей до лінійних
2.1. Лінеаризація квадратичних функційy x 2 ,
Заміна x 2 t
2.2. Лінеаризація зворотних функцій
1
y
x
1
Заміна z
x
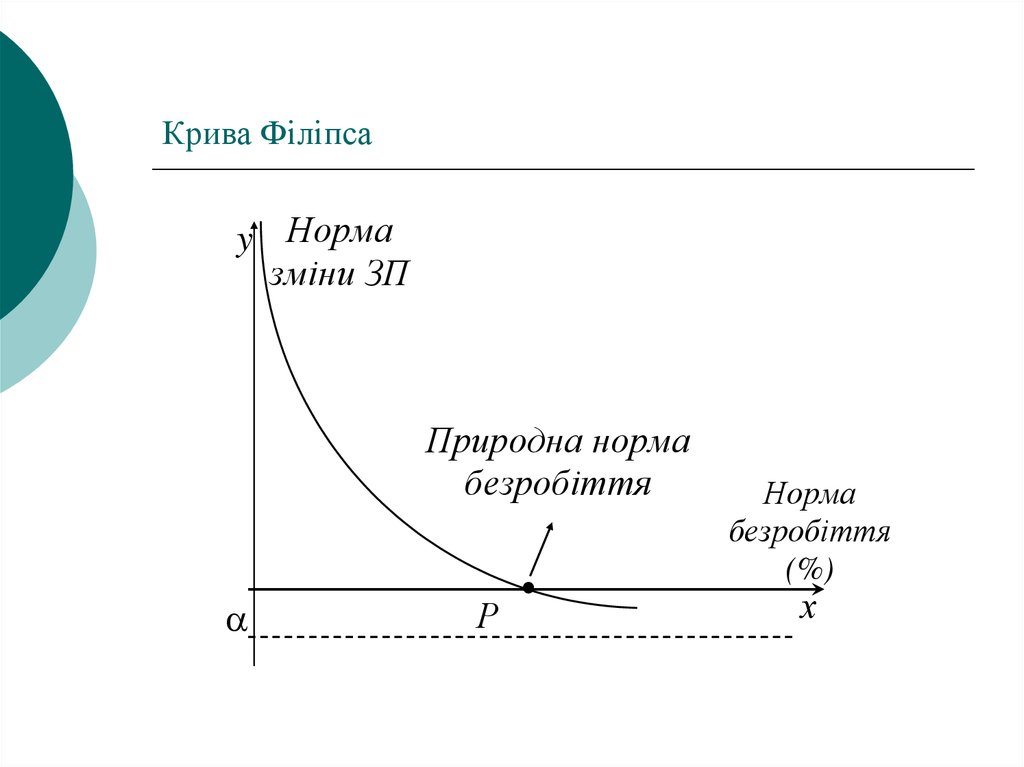
5. Крива Філіпса
y Нормазміни ЗП
(%)
Природна норма
безробіття
Р
Норма
безробіття
(%)
х
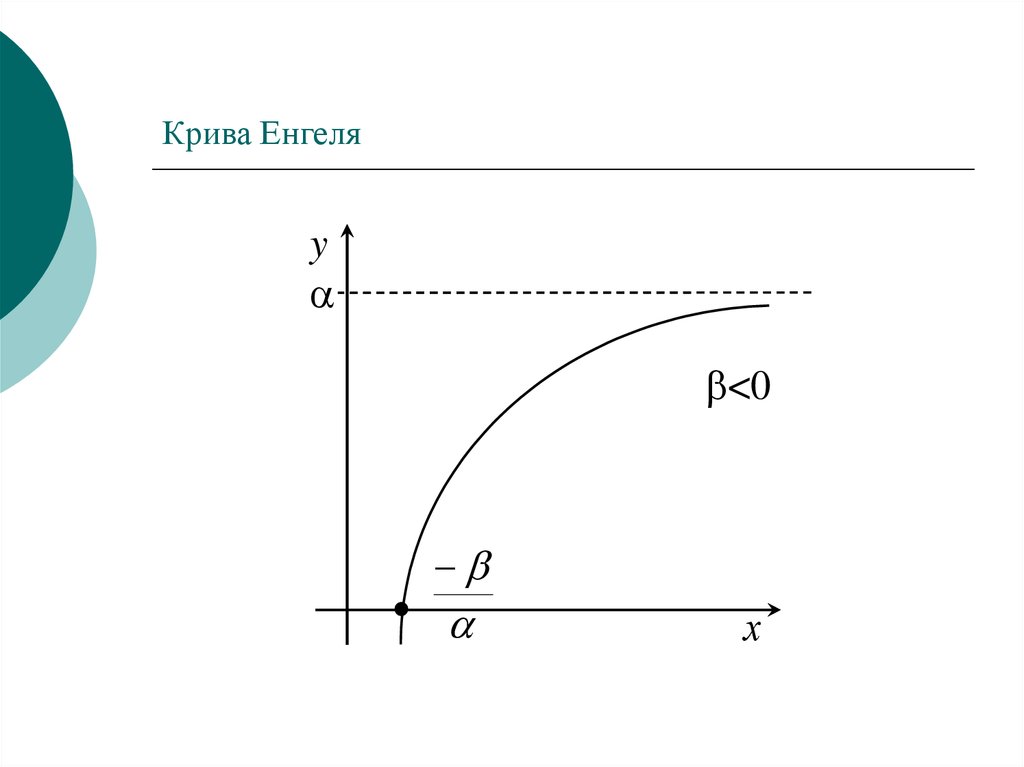
6. Крива Енгеля
y<0
х
7.
2.3. Лінеаризація експоненційних функційy e x
ln y ln x . Заміна ln y y , ln
y x .
2.4. Лінеаризація степеневих функцій
y x
ln y ln ln x . Заміна ln y y , ln , ln x x
y x .
8. Класична лінійна багатофакторна модель
9. План
1. Лінійна багатофакторна економетричнамодель.
2. МНК для багатофакторної
економетричної моделі.
3. Лінійна економетрична модель з трьома
змінними. МНК для моделі з трьома
змінними.
4. Коефіцієнти парної, частинної та
множинної кореляції. Матриця кореляції
10. 1. Лінійна багатофакторна економетрична модель
(1)y 0 1 x1 ... m xm u ,
де y залежна змінна; x1, x2 , …, xm незалежні
змінні; 0 , 1,…, m невідомі детерміновані
параметри; u випадкова складова, збурення,
u u1 , u2 ,..., un .
Оціночне рівняння для даної моделі таке:
(2)
yˆ ˆ0 ˆ1 x1 ... ˆm xm ,
де ˆ0 , ˆ1,…, ˆm оцінки невідомих параметрів 0 ,
1,…, m .
11. 2. МНК для багатофакторної економетричної моделі
y y1 , y2 ,..., yn ,x1 x11 , x12 ,..., x1n ,
x2 x21 , x22 ,..., x2 n , …, xm xm1 , xm 2 ,..., xmn .
n
n
e yi yˆ i
i 1
2
i
i 1
2
2
ˆ
ˆ
ˆ
yi 0 1 x1i ... m xmi ,
n
i 1
F ( ˆ0 , ˆ1 ,... ˆm ) min (3)
12.
F 2 n ( y ˆ ˆ x ... ˆ x ) 0i 0 1 1i
m mi
ˆ
i 1
0
n
F
2 ( y ˆ ˆ x ... ˆ x ) x 0
(4)
i 0 1 1i
ˆ
m mi
1i
1 i 1
F 2 n ( y ˆ ˆ x ... ˆ x ) x 0
i
0
1 1i
m mi
mi
ˆm
i 1
13.
n ˆ ˆ n x ˆ n x ... ˆ n x n y0
1 1i
2 2i
m mi
i
i 1
i 1
i 1
i 1
n
n
n
n
2
ˆ0 x1i ˆ1 x1i ... ˆm xmi x1i yi x1i (5)
i 1
i 1
i 1
i 1
n
n
n
n
2
ˆ0 xmi ˆ1 x1i xmi ... ˆm xmi yi xmi
i 1
i 1
i 1
i 1
14. 3.Лінійна економетрична модель з трьома змінними. МНК для моделі з трьома змінними
m 2:y 0 1 x1 2 x2 u ,
де y залежна змінна; x1, x2 , x3
незалежні змінні; 0 , 1, 3
невідомі детерміновані параметри;
u випадкова складова, збурення,
u u1 , u2 ,..., un .
yˆ ˆ0 ˆ1 x1 ˆ3 x3 ,
де ˆ0 , ˆ1, ˆ3 оцінки невідомих
параметрів 0 , 1, 3 .
15.
n ˆ ˆ n x ˆ n x n yi
1i
2 2i
0 1
i 1
i 1
i 1
n
n
n
n
2
ˆ0 x1i ˆ1 x1i ˆ2 x2i x1i yi x1i . (6)
i 1
i 1
i 1
i 1
ˆ n x ˆ n x x ˆ n x 2 n y x
i 2i
2i
1 1i 2 i
2 2i
0
i 1
i 1
i 1
i 1
Розв’язавши систему (6) отримаємо рівняння
оціночної площини yˆ ˆ0 ˆ1 x1 ˆ3 x3
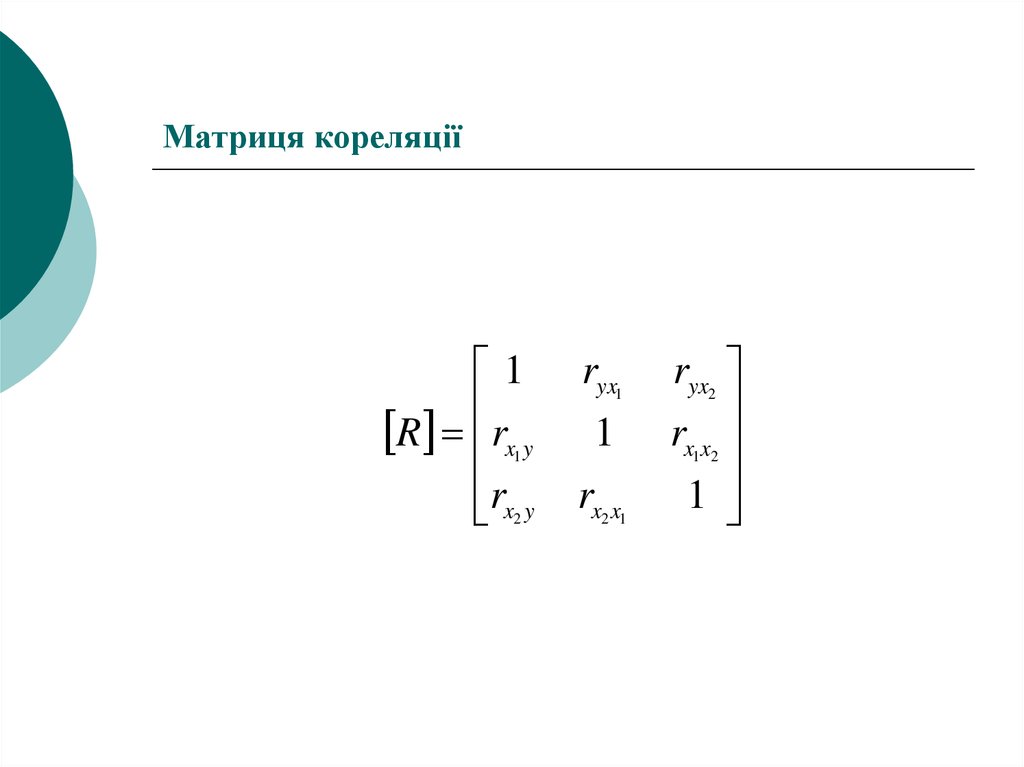
16. 4. Коефіцієнти парної, частинної та множинної кореляції. Матриця кореляції
Коефіцієнт парної кореляції між змінними xk і x jn
rx x
k
j
( xk xk ) ( x j x j )
i
i 1
n
i
n
2
(
x
x
)
(
x
x
)
k
j
k
j
i 1
2
i
i 1
i
17. m=2
( yi y ) ( x1i x1 )ryx
2
2
(
y
y
)
(
x
x
)
i
1i 1
( yi y ) ( x 2 i x 2 )
ryx
( yi y ) 2 ( x 2 i x 2 ) 2
( x1i x1 ) ( x2i x2 )
rx x
( x1i x1 ) 2 ( x2i x2 ) 2
1
2
1 2
18. Матриця кореляції
1R rx y
rx y
1
2
ryx
1
rx x
1
2 1
ryx
rx x
1
2
1 2
19. Коефіцієнти частинної кореляції
ryx . x2
1
ryx ryx rx x
2
1
1 2
1 ryx2 1 rx2x
ryx ryx rx x
1
ryx . x
1
2
1
1 2
2
1 2
1 r 1 r
2
yx2
2
x1x2
.
20. Коефіцієнт множинної кореляції
nR
( yi y )( yˆ i yˆ )
i 1
n
n
( yi y ) ( yˆ i yˆ ) 2
i 1
R2
2
i 1
ryx2 ryx2 2ryx ryx rx x
1
2
1
1 r2x x
1 2
n
( yi yˆ i ) 2
R 2 1 i n1
2
(
y
y
)
i
i 1
2
1 2
21. Оцінений коефіцієнт детермінації
n2
e
i
i 1
R 1
2
(n m 1)
n
( yi y ) 2
i 1
(n 1)
n 1
2
2
.
R 1 (1 R )
n m 1
.


















 mathematics
mathematics








