Similar presentations:
Принципи побудови економетричних моделей.(Лекція 14)
1. ЛЕКЦІЯ 14. ПРИНЦИПИ ПОБУДОВИ ЕКОНОМЕТРИЧНИХ МОДЕЛЕЙ. ПАРНА ЛІНІЙНА РЕГРЕСІЯ
2. План
14.1 Основні задачі економетрії.14.2 Парна лінійна регресія. Метод
найменших квадратів.
14.3 Випадкові збудники в рівнянні лінійної
регресії.
14.4 Умови Гауса-Маркова.
Гомоскедастичні та гетероскедастичні
моделі (самостійна робота).
14.5 Специфікація моделі (самостійна
робота).
3. Парна лінійна регресія. Метод найменших квадратів
y i 0 1 xi i(14.1)
y1 0 1 x1 1 ,
y 2 0 1 x 2 2 ,
............................
y i 0 1 xi i ,
............................
y n 0 1 x n n ,
(14.2)
4.
y Xy1
1
x
1
1 x2
y2
0
y , , X ,
1
1 x
y
n
n
(14.3)
1
2
n
5.
y1 0 * 1 * x1 1 ,y2 0 * 1 * x2 2 ,
............................
yi 0 * 1 * xi i ,
............................
yn 0 * 1 * xn n ,
(14.4)
6.
y X *y1
y2
y ,
y
n
1
1
0 *
, X
1 *
1
(14.5)
x1
x2
,
xn
1
2
n
7.
y 0 1 x ey y1 , y 2 ,..., y n
x x1 , x2 ,..., xn
e e1 , e2 ,..., en
(14.6)
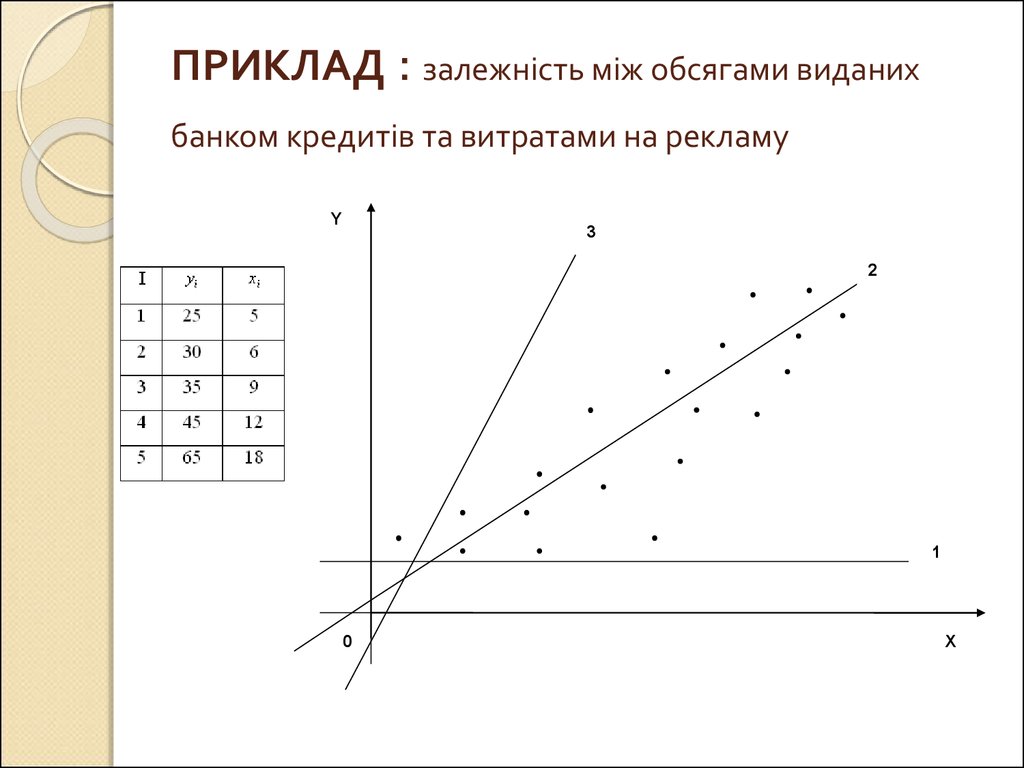
8. ПРИКЛАД : залежність між обсягами виданих банком кредитів та витратами на рекламу
Y3
2
1
0
X
9.
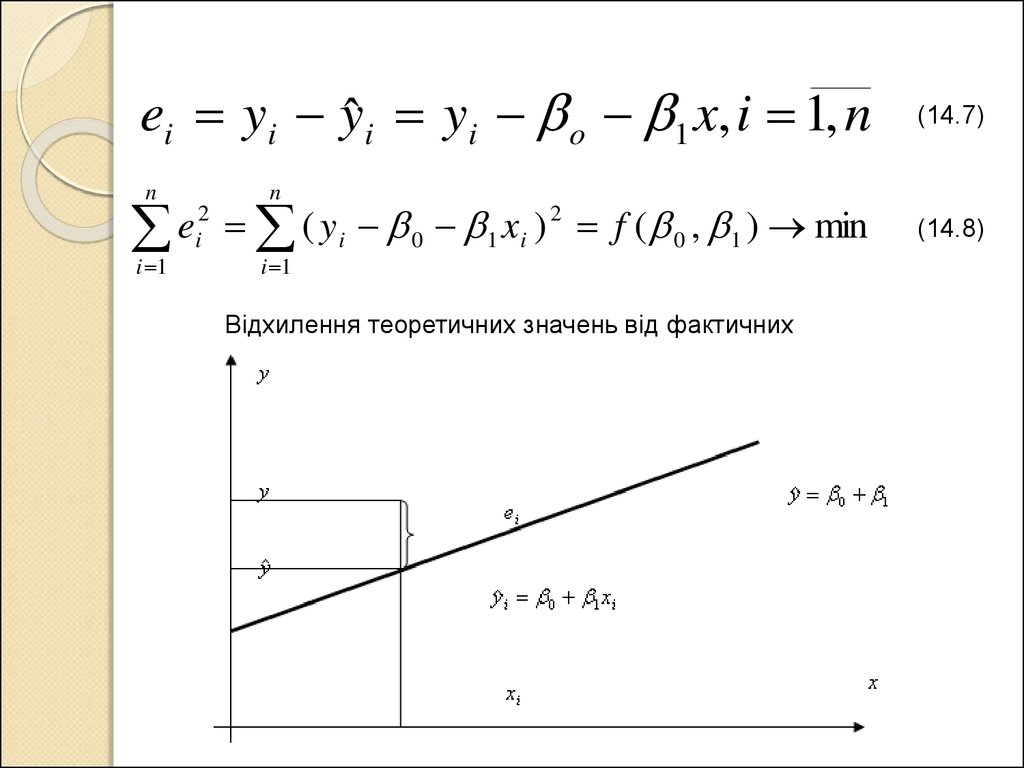
ei yi yˆ i yi o 1 x, i 1, nn
n
2
e
(
y
x
)
i 0 1 i f ( 0 , 1 ) min
i 1
(14.7)
2
i
i 1
Відхилення теоретичних значень від фактичних
(14.8)
10.
n( ei2 )
i 1
0
f ( 0 , 1 )
0;
0
(14.9)
n
( ( yi 0 1 xi ) 2 )
i 1
1
f ( 0 , 1 )
0
1
n 2
( ei )
n
i 1
2 ( y i 0 1 xi ) 0
0
i 1
n
( e 2 )
i
n
i 1
2 xi ( y i 0 1 xi ) 0
i 1
1
(14.10)
11.
yn
x
;
i
0
1
i
i 1
i 1
n
n
n
2
yx
i i
0 xi 1 xi
i 1
i 1
i 1
n
n
(14.11)
12.
nn
1
xi y i
n
x y
i
i 1
i 1
n
i 1
1
x xi
n i 1
i 1
n
i
n
2
(14.12)
2
i
1 n
xi y i x y
n i 1
1
1 n 2
2
xi x
n i 1
(14.13)
1 n
1 n
x xi ; y y i
n i 1
n i 1
13.
n1
cov( x, y ) ( xi x)( y i y )
n i 1
n
1
2
var( x) ( xi x)
n i 1
14.
n 2ei
n
n
2
i 1
y i 0 1 xi y i 0 1 xi 0
0
i 1 0
i 1
(14.14)
n
y i 0 1 xi ei ei
(14.15)
i 1
1 n
1 n
yi 0 1 xi 0
n i 1
n i 1
0 y 1 x
(14.16)
15.
yˆ 0 1 xy yˆ e 0 1 x e
(14.17)
(14.18)
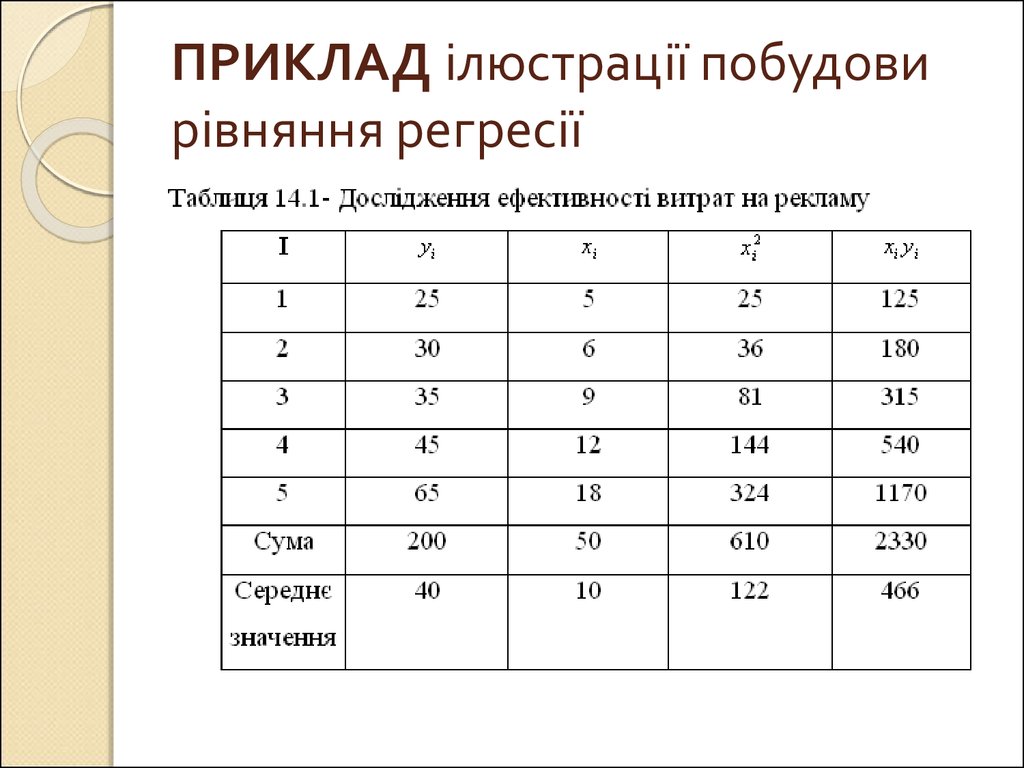
16. ПРИКЛАД ілюстрації побудови рівняння регресії
17.
1 n50
x xi
10;
n i 1
5
1 n
200
y yi
40;
n i 1
5
1 n 2
610
2
var( x) xi x
;
n i 1
5
1 n
2330
cov( x, y ) xi y i x y
400 66;
n i 1
5
cov( x, y ) 66
1
3; 0 y 1 x 40 3 10 10
var( x)
22
yˆ 3x 10
18.
Y 0 1 XY 0 X
1



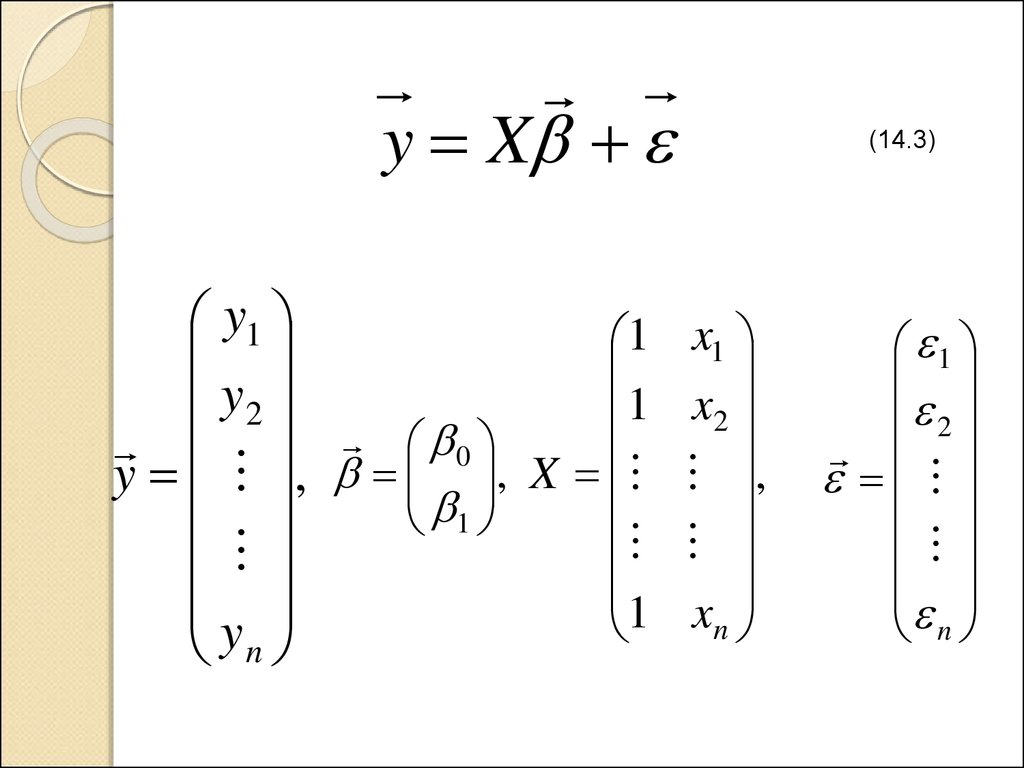

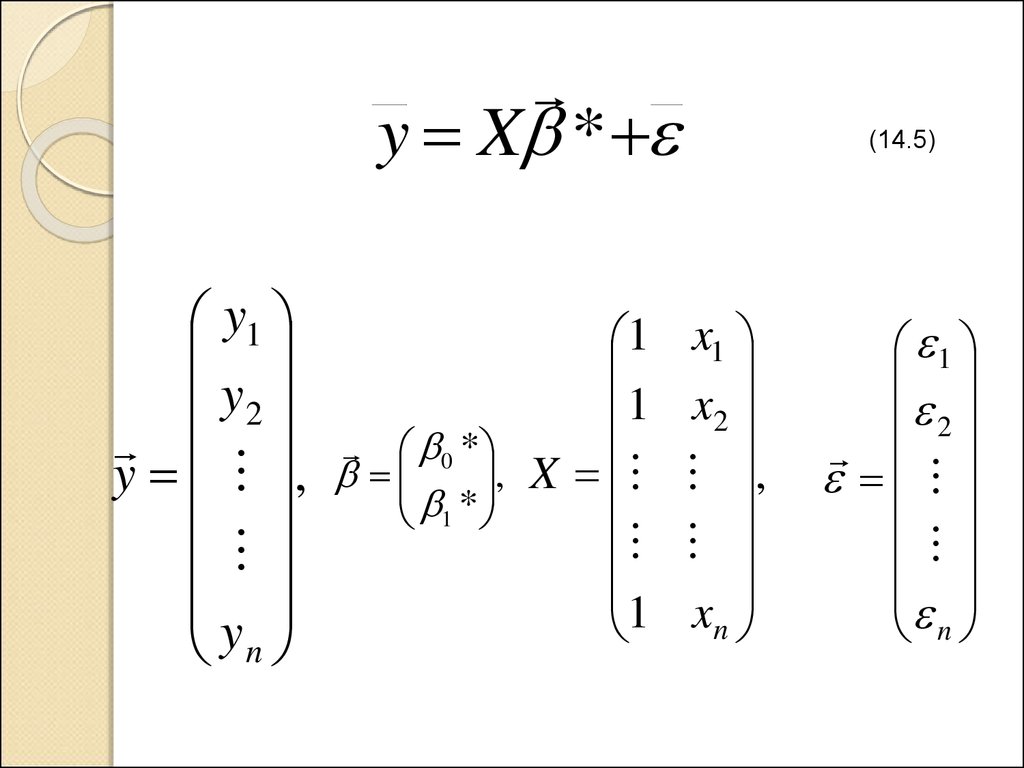
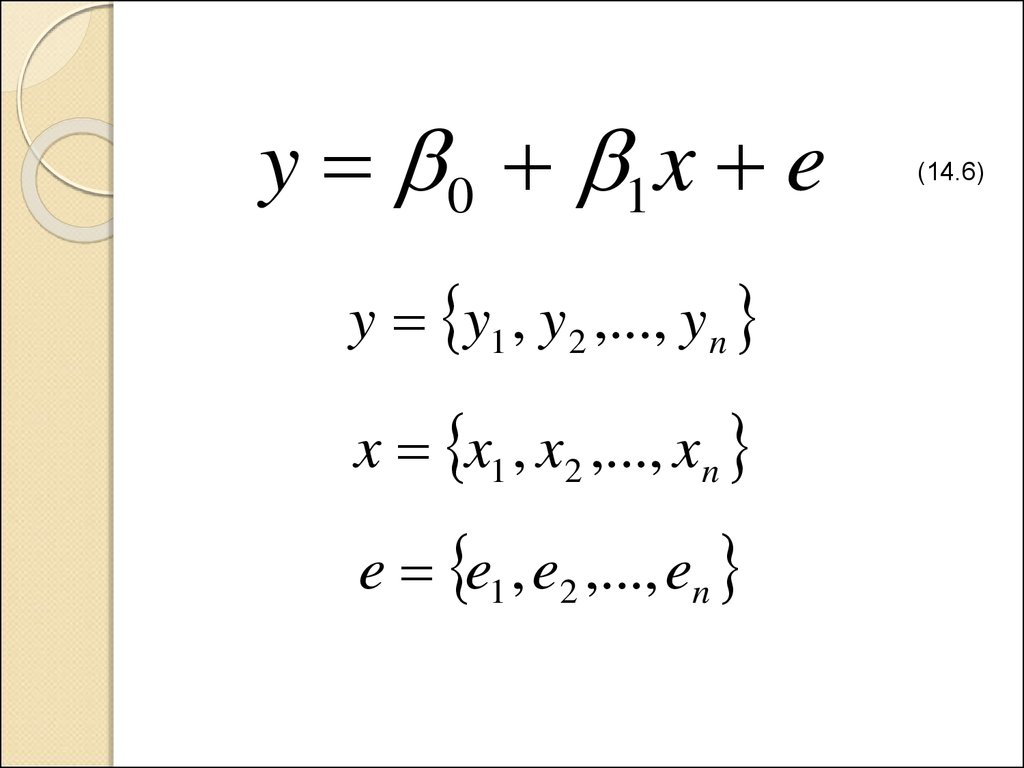

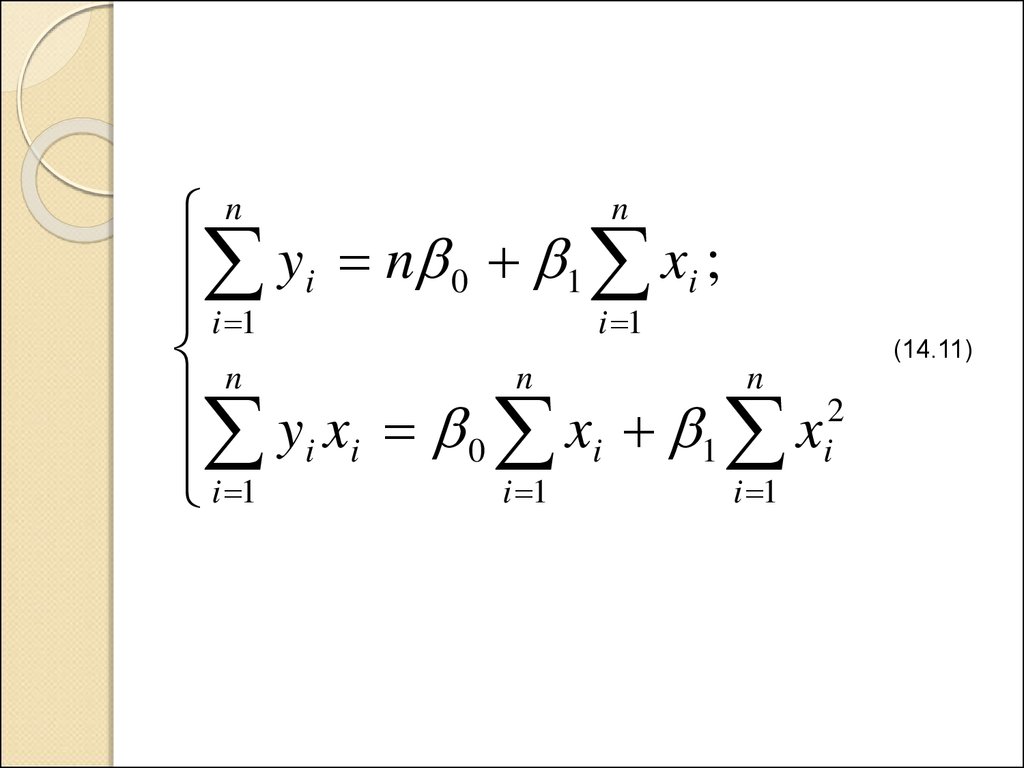
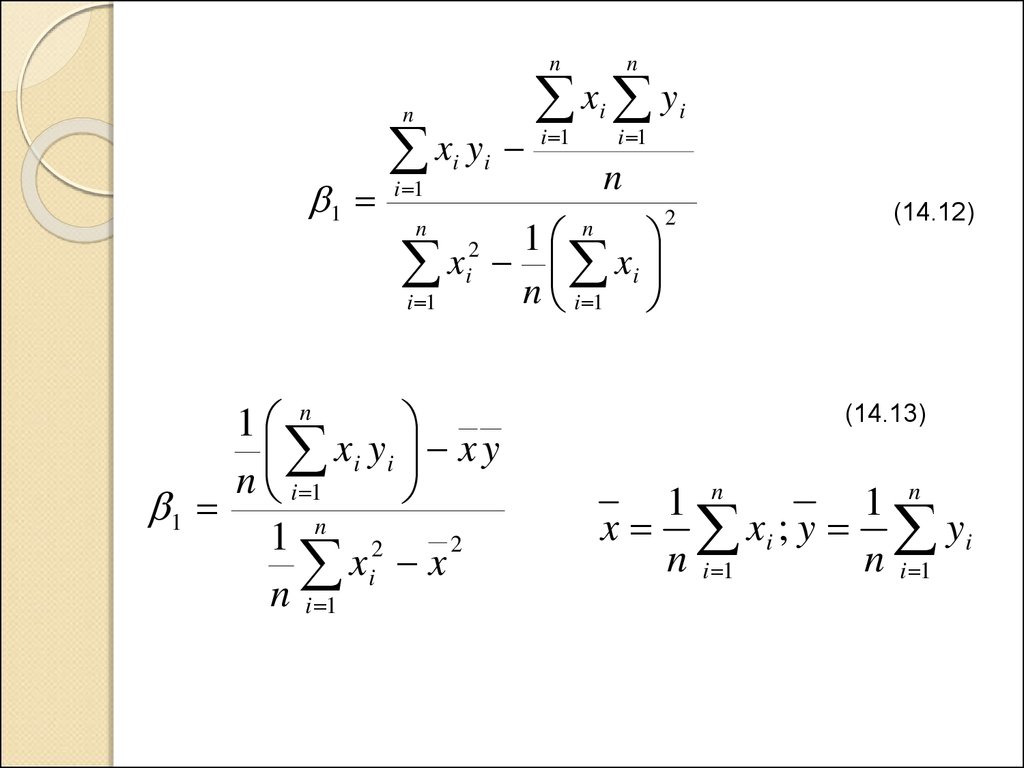
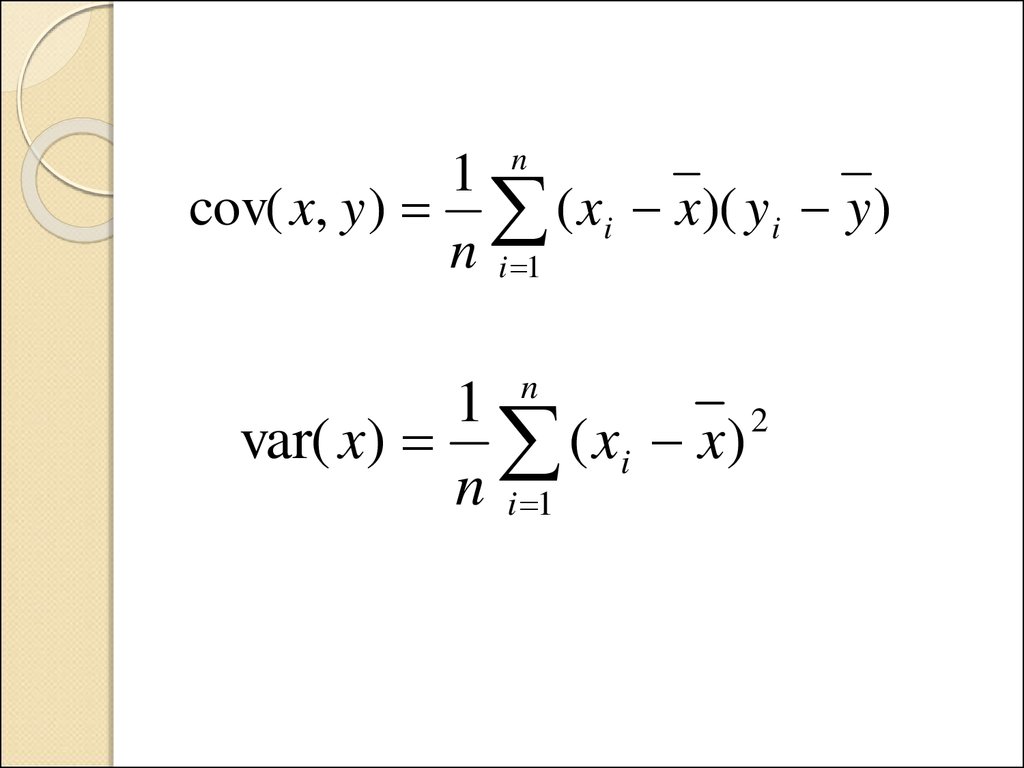

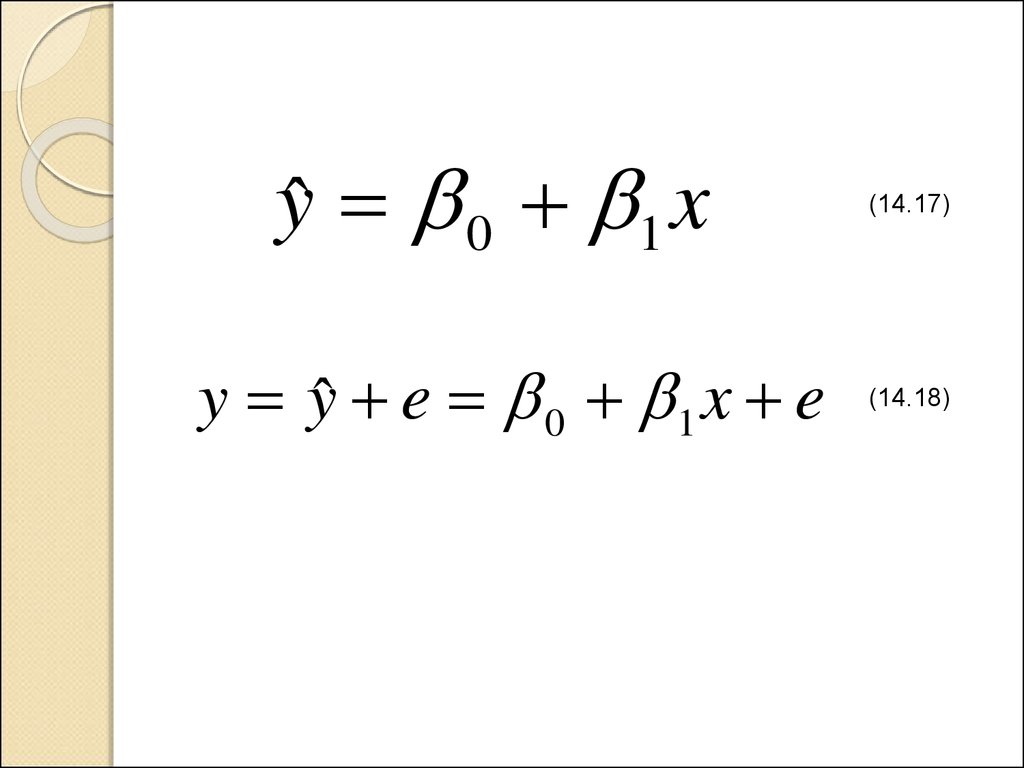
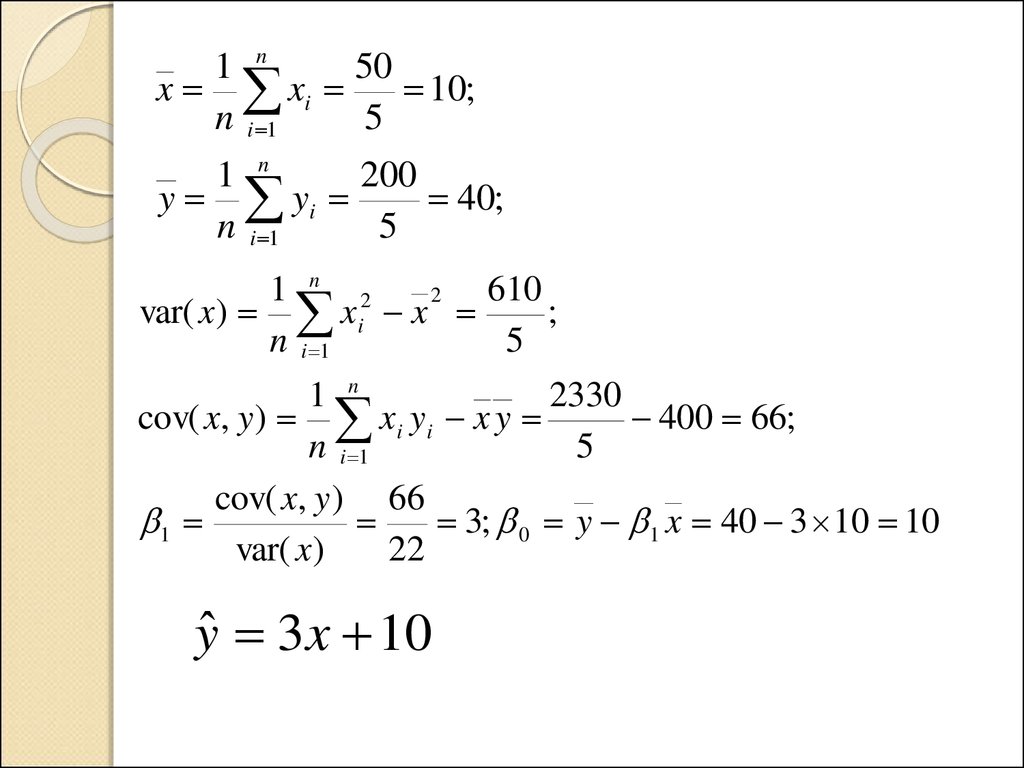
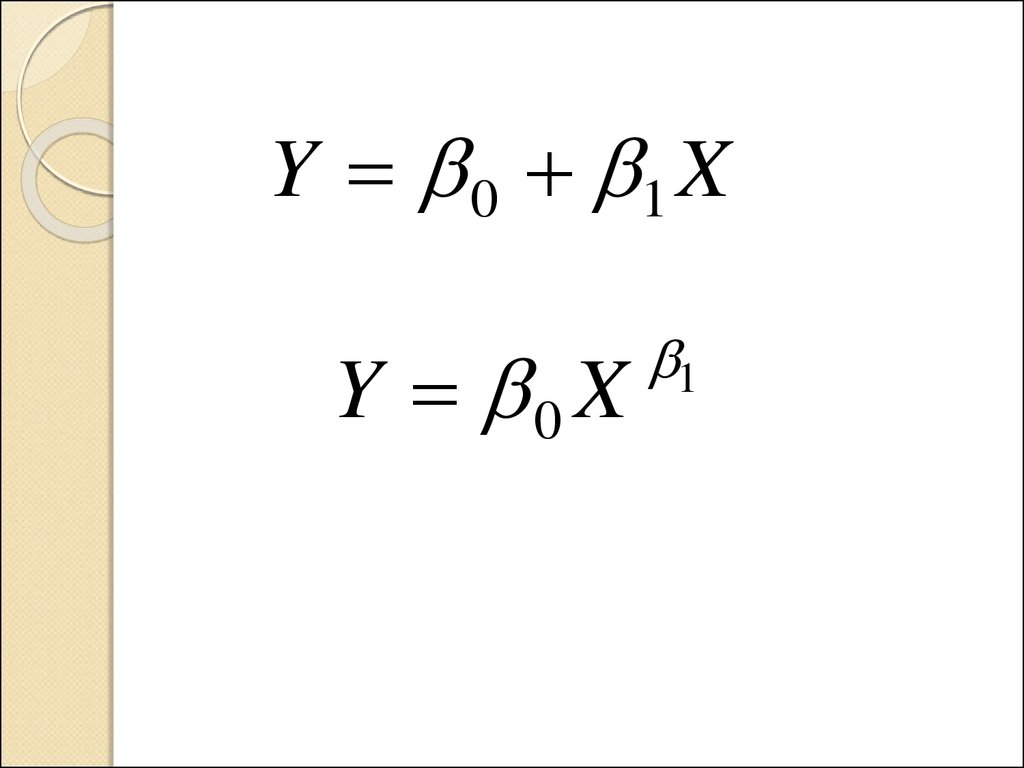
 mathematics
mathematics economics
economics








