Similar presentations:
Предмет та метод економетрії. Однофакторна лінійна економетрична модель
1. Предмет та метод економетрії Однофакторна лінійна економетрична модель
2. Предмет та метод економетрії
За класичним визначенням економетрія ценаука що вивчає кількісні закономірності та
взаємозв’язки економічних обє’ктів і процесів
за допомогою математико-статистичних
методів та моделей.
Економетрія є
інструментом, який дозволяє перейти від
якісного
рівня
аналізу
до
кількісного
(використовуючи
статистичні
дані
досліджуваних величин). Методом економетрії
є статистичні методи (дисперсійний та
кореляційний аналіз і метод регресії).
3. План лекції
1. Регресійната
економетрична
модель,
їх
інформаційна база та етапи побудови.
2. Причини
введення
в
модель
y x u
випадкового доданку u.
3. Знаходження статистичних оцінок однофакторної
економетричної моделі методом найменших квадратів
(МНК).
4.
Регресійна та економетричнамодель, їх інформаційна база та
етапи побудови.
1.
5.
Регресія починається там, де є ряд спостережень наддосліджуваними величинами
y
y1
y2
...
yn
x
x1
x2
...
xn
який є рядом даних, а x і y випадкові величини, при
цьому xi, yi їх практичні реалізації або можливі
значення, n кількість спостережень.
При вимірюванні кількісних ознак можуть бути
отримані два типи рядів даних динамічні та
варіаційні.
6.
Динамічний ряд це послідовність спостережень запроцесом або явищем у рівновіддалені проміжки часу.
Якщо xi значення деякої ознаки економічного процесу
в i й проміжок часу, то динамічний ряд x1, x2, …, xi,…,
xn можна отримати, вимірюючи значення цієї ознаки в
рівновіддалені проміжки часу
Варіаційні ряди це ряди даних, які показують
кількісну міру певної ознаки всіх об’єктів однієї
сукупності, наприклад, оцінки за екзамен студентів
однієї групи.
7.
Етапи побудовирегресійної моделі
1. Ідентифікація змінних
2. Специфікація моделі
3. Оцінка параметрів моделі
4. Аналіз моделі по залишках
8.
Першим етапом побудови регресійної моделі єідентифікація змінних (спостережуваних величин).
Треба визначити яка із спостережуваних величин є
ознакою (залежною величиною, пояснюваною змінною,
функцією), а які величини є незалежними (аргументами,
пояснюючими змінними, факторами). Якщо ми
записуємо
y=f(x),
(1)
то вважаємо, що змінні є ідентифіковані і y, в цьому
випадку, пояснювана змінна, x пояснююча.
9.
Другим етапом до побудови регресійної моделі єспецифікація моделі, а саме: на основі даних
ряду досліду потрібно визначити аналітичну
форму зв'язку (1).
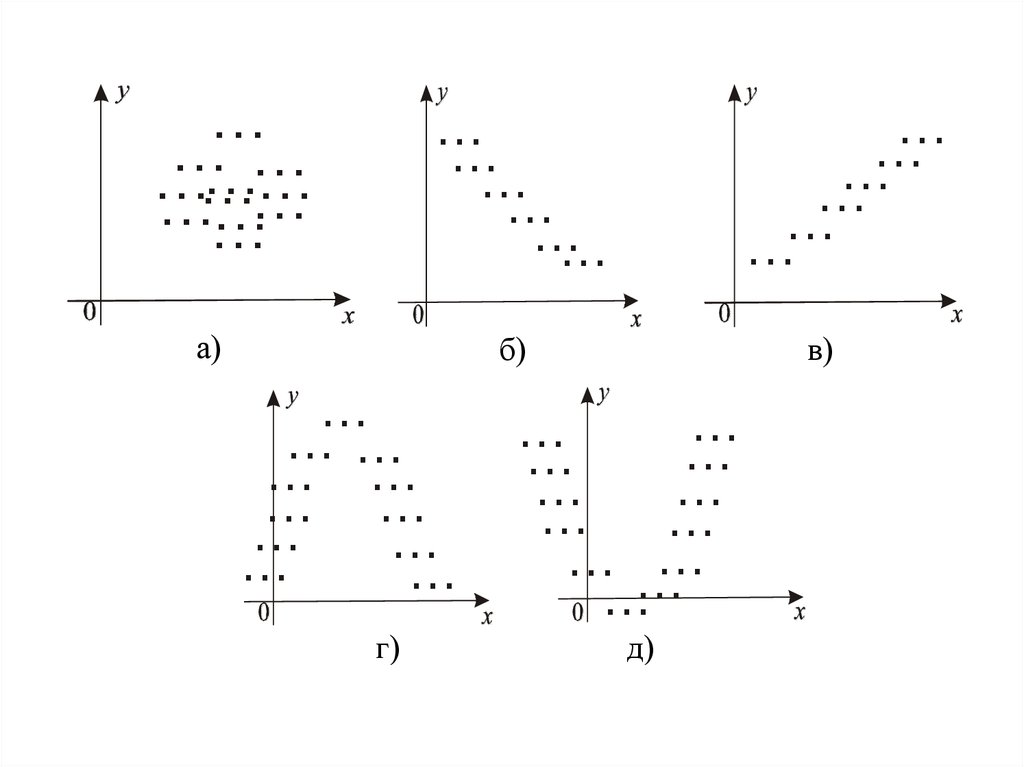
Найчастіше специфікацію проводять з допомогою
хмарки точок (діаграми розсіювання). На осі
абсцис відзначають значення незалежної змінної
(x), на осі ординат значення залежної змінної (y).
За виглядом діаграми розсіювання можна
висунути гіпотезу про лінійність чи нелінійність
зв’язку між змінними.
10.
……
…
…
…
…
…
……
…
…
…
…
…
…
…
…
……
……
…
а)
б)
в)
…
…
…
……
…
…
… …
…
…
…
…
… …
… …
…
……
…
…
…
г)
д)
11.
Нехай залежність між y та x лінійна, тоді (1) наберевигляду:
(2)
y x u
де α, невідомі детерміновані параметри; y вектор
спостережень за залежною змінною, y y1 , y2 ,..., yn ; x
вектор спостережень за незалежною змінною,
x x1 , x2 ,..., xn ; u випадкова складова, збурення,
u u1 , u2 ,..., un .
Рівняння (2) називається економетричною
моделлю, якщо у та х є кількісними показниками деяких
економічних явищ чи процесів. Таким чином, рівняння
регресії перетворюється в економетричне, якщо воно
налагоджує зв'язок між кількісними показниками
об'єктів економіки.
12. 2) Причини введення випадкового доданку u
1) в економетричних моделях на ознаку діє такакількість факторів, яка значно перевищує кількість
дослідів, замірів, об'єм. По тій причині з ситуації
виходять так: з усіх змінних виділяють 1, 2 чи 3
значущих, а решту об'єднують в одну, яку називають
випадковою величиною.
2) полягає в тому, що предметом економетрії є
людське суспільство з його багатогранністю смаків і
уподобань, які неможливо нічим, крім випадкової
величини відобразити.
3) полягає у похибці вимірювання.
13. 3) Знаходження статистичних оцінок однофакторної економетричної моделі методом найменших квадратів (МНК).
3-ій етап знаходження оцінок параметрів моделі.Практично моделі (2) не існує, її потрібно оцінити
деяким рівнянням
(3)
yˆ ˆ ˆx ,
де ˆ та ˆ називаються статистичними оцінками
параметрів та і знаходяться на основі вибіркових
даних.
14.
ˆ перетин прямої з віссю ординат, ˆ нахил прямоїдо осі абсцис. ˆ також визначає зміну результативного
показника при зміні х на одиницю. Значення yˆi
показують середнє значення залежної змінної y при
заданому xi у припущенні, що єдиною причиною зміни
y є змінна х, а випадкова збурена змінна u прийняла
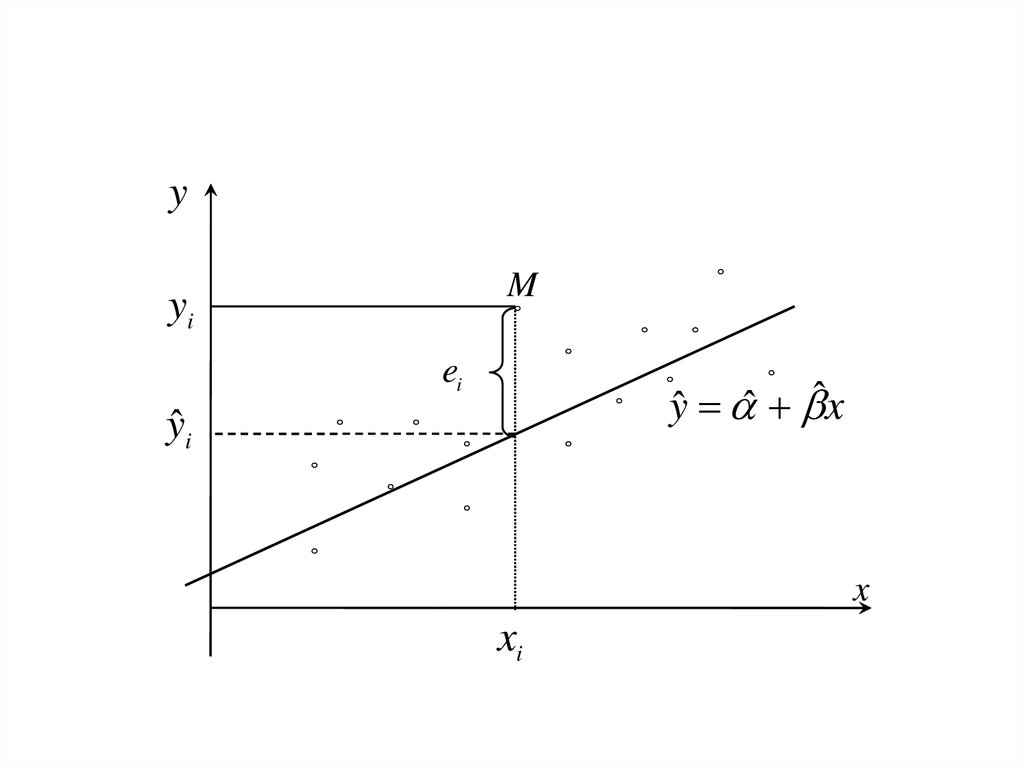
значення, рівне нулеві. Розкид спостережених значень
змінної y довкола yˆi зумовлений впливом множини
неврахованих факторів. Різниця між yi і розрахунковим
yˆi називається залишком (відхиленням), який дає
числову оцінку значення збурення u. Отже, він
визначається ei yi yˆ i , i 1, n . Чим менше значення ei ,
тим краще підібрана пряма.
15.
yM
yi
ei
yˆ ˆ ˆx
yˆ i
x
xi
16.
2ˆ
e yi ˆ xi f ˆ , ˆ min
n
i 1
2
i
n
i 1
n
ei2
i 1 2 n y ˆ ˆx 0;
i
i
i 1
ˆ
n
ei2
i 1 2 n x y ˆ ˆx 0.
i i
i
ˆ
i 1
n
n
yi n ˆ ˆ xi ;
i 1
i 1
n
n
n
yi xi ˆ xi ˆ xi 2 ,
i 1
i 1
i 1
(4) – система нормальних рівнянь МНК
(4)
17.
Обчислення статистичних оцінок МНК через прирости(відхилення від середніх арифметичних)
n
yi
i 1
n
y
n
ˆ ˆ
n
yi
i 1
xi
i 1
n
xi
n
, x
i 1
.
n
n
y ˆ ˆ x .
Віднімемо (6) від (3):
yˆ i y ˆ ( xi x)
yˆ i y ˆ ( xi x)
yi y yi , xi x xi , тоді yˆ i y ˆ xi .
(6)
(6')
18.
2ˆ
ˆ
e yi y xi yi xi f ˆ min
n
2
i
i 1
n
i 1
2
n
i 1
n
d ei2
i 1 2 n x y ˆ x 0.
i i
i
ˆ
i
1
d
n
n
2
ˆ
x
y
i i
xi .
i 1
i 1
n
ˆ
xi yi
i 1
n
2
xi
,
(7)
ˆ y ˆ x .
i 1
n
cov(
x
,
y
)
1
ˆ
, cov( x, y ) ( xi x )( yi y ) ,
n i 1
var( x)
1 n
2
( x) var( x) ( xi x ) 2 .
n i 1
(7')
19. ОСНОВНІ РЕЗУЛЬТАТИ ТЕМИ
1. Однофакторна економетрична модель:y x u .
2. Оціночне рівняння:
yˆ ˆ ˆx .
3. МНК:
n
n
yi n ˆ ˆ xi ;
i 1
i 1
3.1
n
n
n
yi xi ˆ xi ˆ xi 2 ,
i 1
i 1
i 1
n
3.2
ˆ
xi yi
i 1
n
2 xi
i 1
, ˆ y ˆ x .
20. СТАТИСТИЧНА ПЕРЕВІРКА ОЦІНОК ОДНОФАКТОРНОЇ ЕКОНОМЕТРИЧНОЇ МОДЕЛІ
21. План
1. Стандартна похибка оцінки за рівняннямеконометричної моделі.
2. Коефіцієнт детермінації та коефіцієнт кореляції.
3. Основні припущення при використанні МНК.
4. Загальні відомості про статистичні оцінки.
5. Незміщеність і ефективність оцінок МНК.
6. Перевірка нульових гіпотез стосовно r.
7. Побудова інтервалів довір’я рівняння
економетричної моделі.
8. Перевірка нульових гіпотез і довірчі інтервали
параметрів α і β.
9. Перевірка моделі на адекватність
22. 1. Стандартна похибка оцінки за рівнянням економетричної моделі.
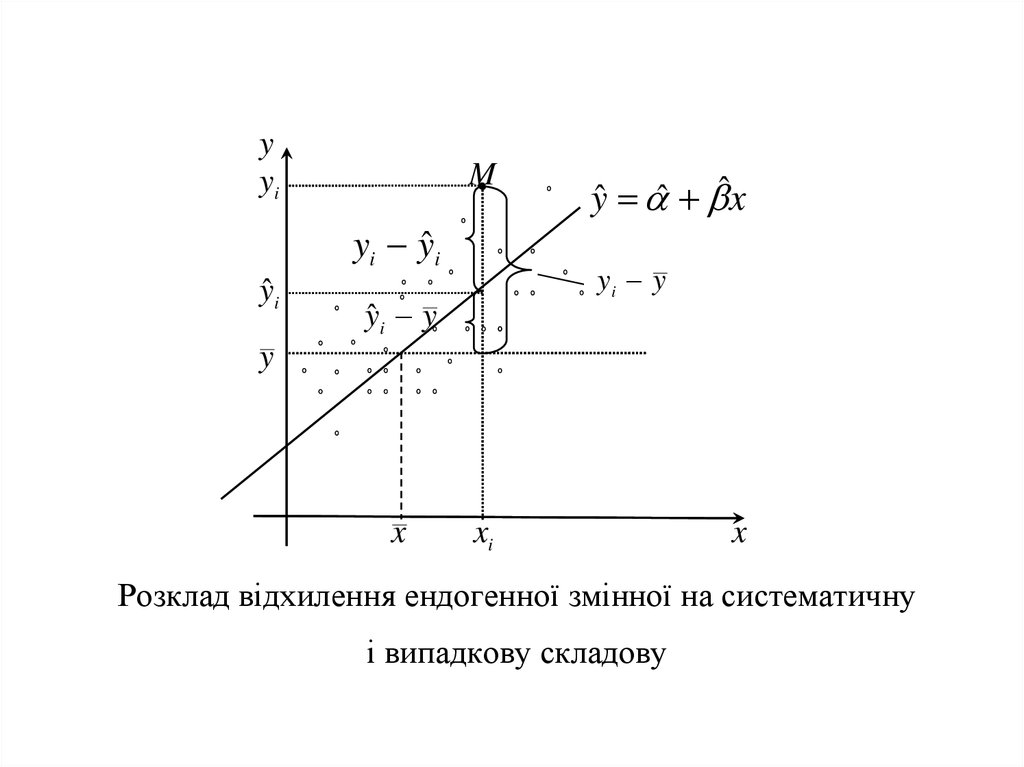
Основна ідея аналізу оцінок базується на тому, щозначення змінної y визначаються двома компонентами:
1.Систематичною складовою x ;
2. Випадковою складовою u .
23.
yyi
M
yi yˆ i
yˆ i
yˆ ˆ ˆx
yi y
yˆ i y
y
x
xi
x
Розклад відхилення ендогенної змінної на систематичну
і випадкову складову
24.
( yi y ) ( yˆ i y ) ( yi yˆ i )n
n
(8)
n
n
2
(
y
y
)
(
y
y
)
2
(
y
y
)(
y
y
)
(
y
y
)
ˆ
ˆ
ˆ
ˆ
i
i
i
i i
i
i
2
i 1
2
i 1
i 1
n
i 1
n
n
2
2
2
(
y
y
)
(
y
y
)
(
y
y
)
ˆ
ˆ
i
i
i i
i 1
i 1
i 1
СКЗ СКП СКН
n
де CKЗ ( yi y ) 2 загальна сума квадратів;
i 1
n
CKП ( yˆ i y ) 2 пояснена сума квадратів;
i 1
n
CKН ( yi yˆ i ) 2 непояснена сума квадратів.
i 1
n
( yi y )
i 1
n
n
2
( yˆ i y )
i 1
n
n
2
( yi yˆ i ) 2
i 1
n
(9)
25.
n2
(
y
y
)
i
i 1
n
2
заг
. загальна дисперсія;
n
2
(
y
y
)
ˆi
i 1
n
2
поясн
. пояснена дисперсія;
n
( yi yˆ i ) 2
i 1
n
2
непоясн
. непояснена дисперсія.
2заг.= 2поясн.+ 2непоясн.
(10)
26.
Середні квадрати CKП і CKН :n
CKП
( yˆ i y )
n
2
i 1
1
CKН
2
(
y
y
)
ˆ
i i
i 1
n 2
Стандартна похибка оцінки за
рівнянням економетричної моделі:
n
yx
2
(
y
y
)
ˆ
i i
i 1
.
n 2
0 yx заг .
(11)
.
27. 2.Коефіцієнти детермінації та кореляції
22
поясн
.
.
1 2 . непоясн
2
заг .
заг .
(12)
Коефіцієнт детермінації
2
.
d r 2 поясн
2
заг
.
0 d 1
(13)
28.
Коефіцієнт кореляції1 n
( xi x )( yi y )
cov( x, y )
n i 1
,
r
n
n
1
x y
2 1
2
(
x
x
)
(
y
y
)
i
i
n i 1
n i 1
1 r 1
x
cov( x, y )
ˆ
r
(15)
var( x) var( y )
y
d r 2.
(16)
2
2
поясн
.
непоясн.
r d
1
2
2
заг
.
заг .
(14)
(17)
29. 3. Основні припущення при використанні МНК
Припущення 1.M (ui ) 0, i 1, n.
Припущення 2.
M (ui2 ) var(ui ) 2 .
Припущення 3.
M (ui u j ) 0, i j
або cov(ui , u j ) 0, i j .
Припущення 4.
M ( xi ui ) 0 або cov( xi , ui ) 0.
Припущення 5. Випадкова змінна u розподілена по
нормальному закону.
30. 4. Загальні відомості про статистичні оцінки
Точковою оцінкою оцінюваного параметраназивається знайдене значення оцінки (в нашому
випадку це ˆ і ˆ ).
Інтервальною оцінкою оцінюваного параметра
називається інтервал, в межах якого з наперед
заданою імовірністю лежить істинне значення
параметра.
Незміщеною оцінкою оцінюваного параметра
називається така оцінка ˆ математичне сподівання
якої дорівнює оцінюваному параметру, тобто
M ( ˆ ) .
31.
Ефективною оцінкою оцінюваного параметраназивається така оцінка ˆ , яка при заданому об’ємі
2
вибірки має найменшу дисперсію ( ). Ефективна
оцінка забезпечує стійкість економетричної моделі
на предмет відсутності систематичних додатних чи
від’ємних відхилень розрахункових значень від
фактичних при малих виходах за границі вибірки.
Спроможною оцінкою оцінюваного параметра
називається така оцінка ˆ , яка при збільшенні
об’єму вибірки до нескінченності по імовірності як
завгодно близько наближається до параметра :
lim p ˆ 1, де як завгодно мале число.
n
32. 5.Незміщеність і ефективність оцінок МНК
nˆ
( xi x ) yi
i 1
n
2
(
x
x
)
i
n
wi yi ,
(20)
i 1
i 1
де wi
( xi x )
n
2
(
x
x
)
i
n
. wi 0 ,
i 1
n
wi
i 1
i 1
n
n
i 1
i 1
1
2
n
2
(
x
x
)
i
i 1
wi ( xi x ) wi xi 1.
1
ˆ
ˆ y x ( x wi ) yi
i 1 n
n
(21)
,
33.
M ( ˆ ) M ( wi yi ) M wi ( xi ui )i 1
i 1
n
n
n
M wi wi xi wi ui )
i 1
i 1
i 1
n
M 0 1 wi ui )
i 1
n
n
n
M ( ) wi M (ui ) .
i 1
n
1
1
ˆ ( x wi ) yi ( x wi ) ( xi ui )
i 1 n
i 1 n
n
34.
1x wi x x wi xi ( x wi ) ui
i 1
i 1
i 1 n
n 1
( x wi ) ui
i 1 n
n 1
M ( ˆ ) M ( x wi ) ui
i 1 n
n 1
M M ( x wi ) ui
i 1 n
n 1
( x wi ) M (ui ) .
i 1 n
n
n
n
35.
nn
2
2
2
ˆ
M ( ) M ( wi ui ) e ( wi )
i 1
i 1
2
ˆ
2
e2
n
2
(
x
x
)
i
i 1
2
2
(
y
y
)
e
ˆ
2
i
i
де e
.
n 2
n 2
1
M ( ˆ ) ( x wi ) 2
i 1 n
n
2x n
2 1
2
2
e x (wi ) wi
n i 1
i 1
n
2
ˆ
2
2
e
n
(22)
36.
n2ˆ
2 2
x
i e
i 1
n
n ( xi x )
.
(23)
2
i 1
Примітка. При розв’язуванні контрольних і
лабораторних робіт для спрощення розрахунків
можна використовувати для обрахунків дисперсій
2ˆ і 2ˆ наступні формули:
n
2
ˆ
n
2
непоясн.
2
(
x
x
)
i
i 1
,
2ˆ
2 2
x
i непоясн.
i 1
n
n ( xi x ) 2
i 1
.
37. 6.Перевірка нульових гіпотез стосовно r
H 0 : rген 0Н1: rген 0, між змінними y та x є суттєвий зв’язок.
r n 2
tемп
1 r2
t кр (k=n 2, ) за таблицями розподілу Стьюдента.
tемп tкр – Н0 слід відкинути, прийняти Н1,
вибірковий коефіцієнт кореляції r вважати
статистично значущим.
38. 7. Побудова інтервалів довір’я рівняння економетричної моделі
P( ˆ k ˆ ˆ k ˆ ) 1Гранична похибка оцінки за рівнянням
економетричної моделі
(24)
yx yx t p ,
де t p імовірнісний коефіцієнт
( 2Ф(t p ) p , де Ф(t p ) функція Лапласа).
(25)
yˆ i yx yi yˆ i yx
ˆ ˆxi yx yi ˆ ˆxi yx ,
( ˆ yx ) ˆxi yi ( ˆ yx ) ˆxi . (26)
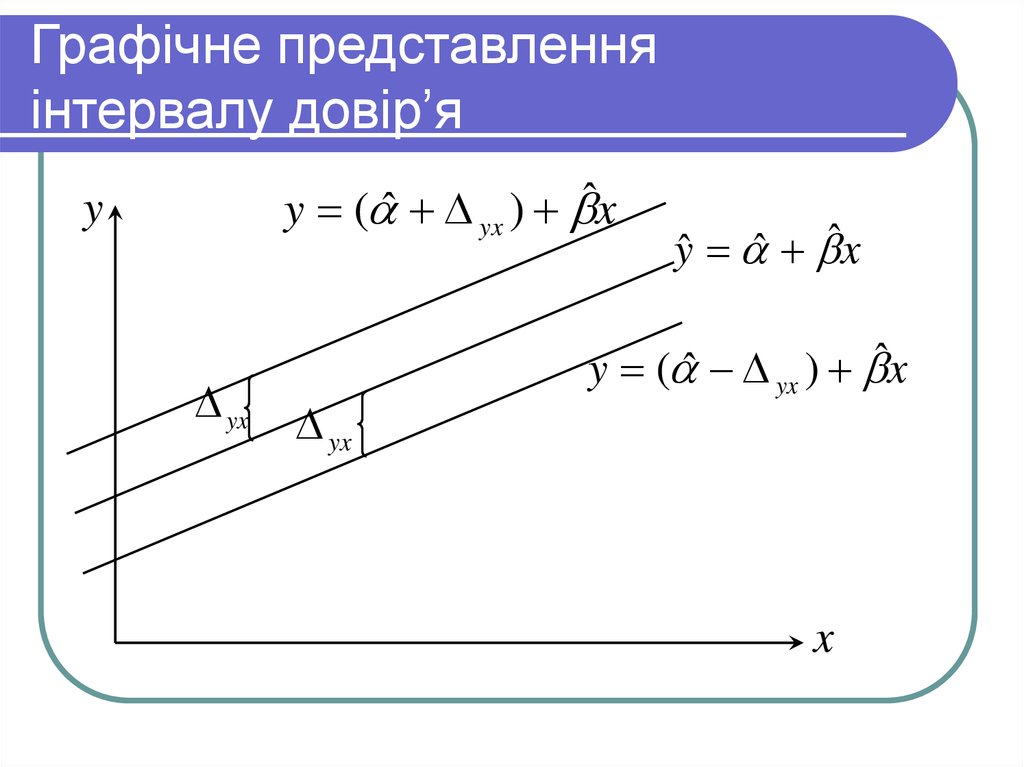
39. Графічне представлення інтервалу довір’я
y ( ˆ yx ) ˆxy
yx
yx
yˆ ˆ ˆx
y ( ˆ yx ) ˆx
x
40. 8. Перевірка нульових гіпотез і довірчі інтервали параметрів α і β
H 0 : 0. H 1 : 0.H 0 : 0. H 1 : 0.
tемп
tемп tкр ( ,
ˆ
,
ˆ
k n 2)
tемп
-
ˆ
.
ˆ
відповідну
оцінку
вважають статистично значущою.
tемп tкр то оцінка є статистично не значущою.
41.
ˆ ˆ t p ,ˆ ˆ t p ,
де t p імовірнісний коефіцієнт, який знаходиться за
таблицями нормального розподілу; 2ˆ , 2ˆ
дисперсії оцінок ˆ та ˆ
Довірчий інтервал для :
ˆ ˆ ˆ ˆ
Довірчий інтервал для :
ˆ ˆ ˆ ˆ .
42. 9.Перевірка моделі на адекватність
1) Розраховуємо величину F-відношення:n
( yˆ i y ) 2
i 1
CKП
F
n 1
CKН ( y yˆ ) 2
i
i
i 1
n 2
n
(n 2) ( yˆ i y ) 2
i 1
n
2
(
y
y
)
ˆ
i i
i 1
r2 n 2
. (27)
2
1 r 1
2) Задаємо рівень значущості (або 100%).
43.
1) Знаходимо Fкр за стат. таблицями F розподілуФішера з (1, n 2) ступенями вільності і .
2) Якщо F Fкр , то ми відкидаємо H 0 з ризиком
помилитися не більше ніж в % випадків, і
приймаємо,
що
побудоване
рівняння
економетричної моделі адекватне реальній
дійсності. В протилежному випадку F Fкр H 0
приймаємо і вважаємо, що побудована модель
неадекватна. Тоді необхідно, можливо, будувати
нелінійну модель або ввести додаткові фактори.
44. Прогнозування
yˆ n 1 ˆ ˆxn 1.2
(
x
x
)
1
( ˆ ˆxn 1 ) t yx 1 n n 1
.
n ( x x )2
i 1
i
(Нижня межа інтервалу песимістичний прогноз,
верхня оптимістичний).
M ( yn 1 ) xn 1.
2
(
x
x
)
1
( ˆ ˆxn 1 ) t yx
n n 1
n ( x x )2
i 1
i




























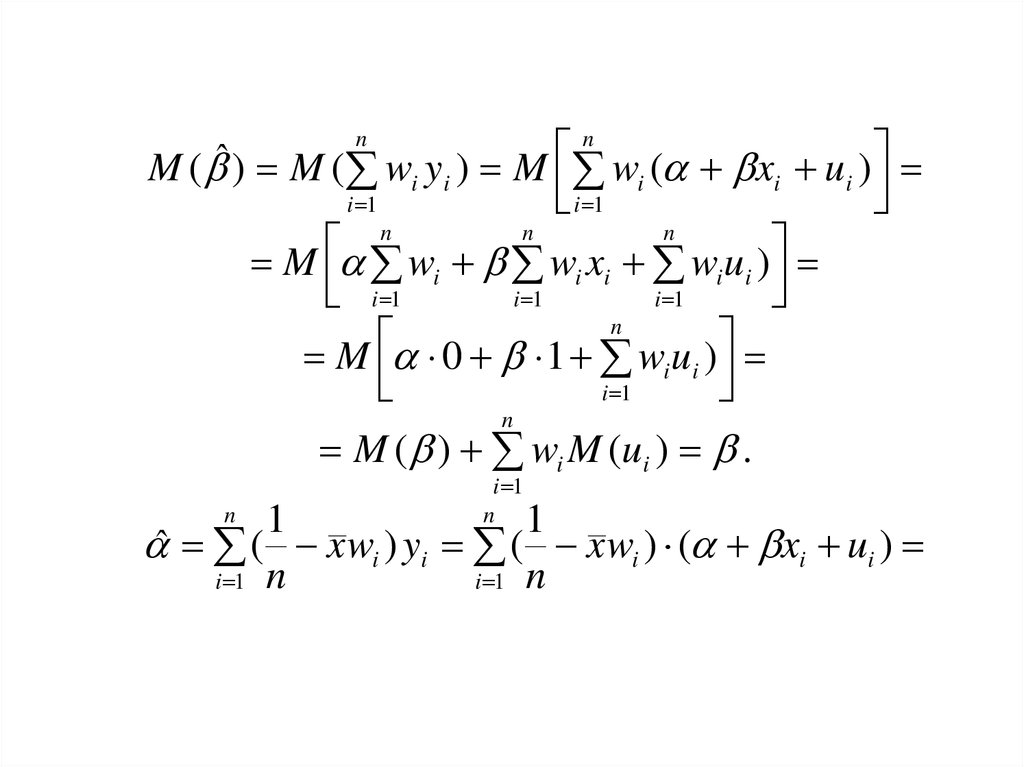
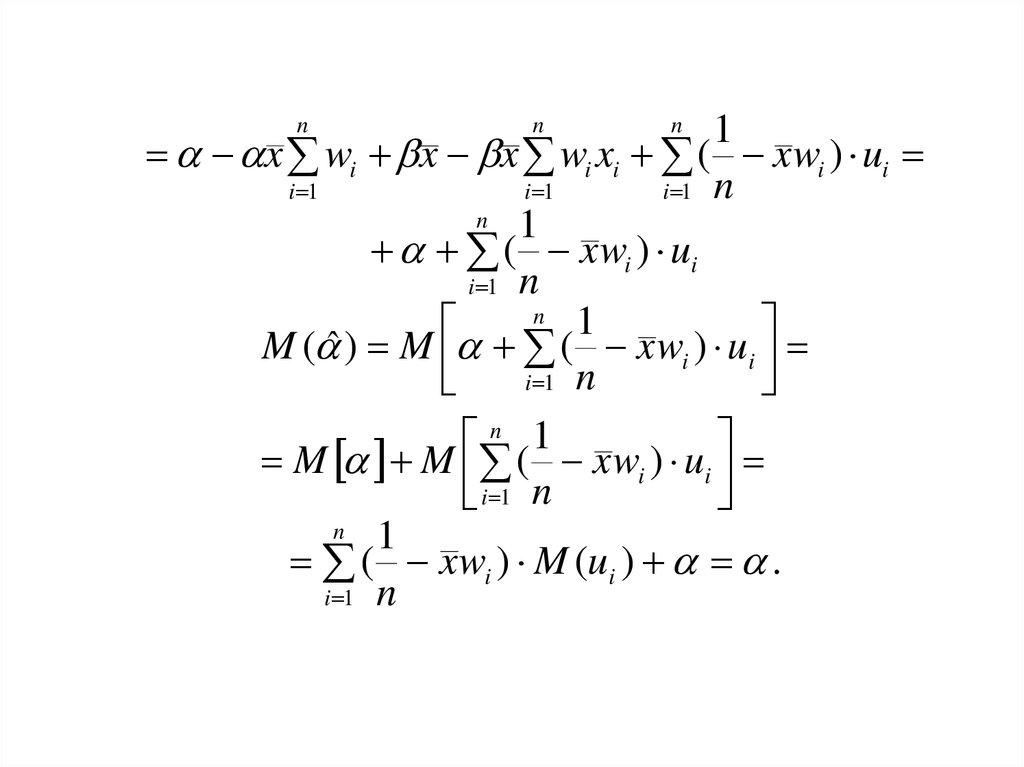
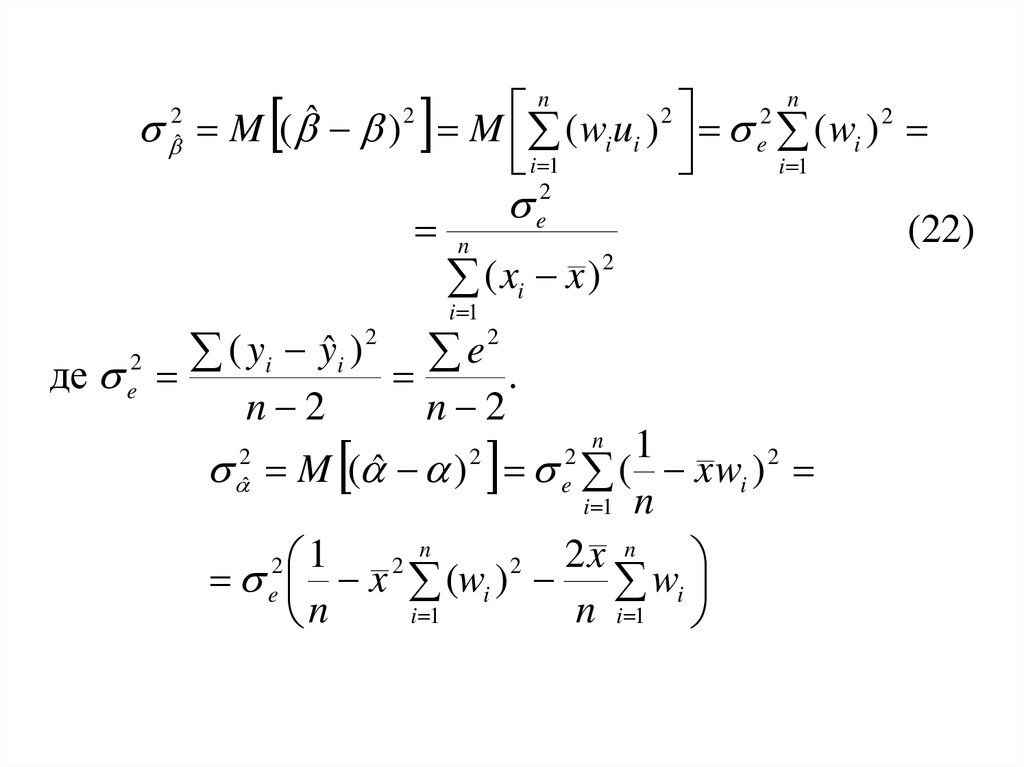








 economics
economics








