Similar presentations:
Матричний підхід до лінійної багатофакторної моделі
1. Матричний підхід до лінійної багатофакторної моделі
2. План
1.2.
3.
4.
Лінійна багатофакторна економетрична
модель і основні її припущення в
матричній формі.
МНК в матричній формі.
Дисперсійно-коваріаційна матриця .
Прогнозування за економетричною
моделлю.
3. 1.Лінійна багатофакторна економетрична модель і основні її припущення в матричній формі
(1)yi 0 1 x1i 2 x2i ... m xmi ui ,
де yi і-е значення залежної змінної; x ji і-е
значення j -ої незалежної змінної; 0 , 1,…, m
невідомі детерміновані параметри; ui і-е значення
випадкової змінної.
4.
y1 0 1 x11 2 x21 ... m xm1 u1 ;y x x ... x u ;
2
0
1 12
2 22
m m2
2
(2)
yn 0 1 x1n 2 x2 n ... m xmn u n .
(3)
Y Xβ U ,
0
y1
u1
1 x11 x21 xm1
y
u
1 x
x
x
12
22
m2
; β 1 ; U 2 .
Y 2 ; X
y
n
1 x
1n
x2 n
x mn
m
u
n
5.
Припущення 1.u1 M (u1 ) 0
u M (u ) 0
2
.
M 2
u M (u ) 0
n
n
Припущення 2.
u1
u
M (UU ) M 2 u1
u
n
u 2 u n ,
6.
20
M (UU )
0
0
2
0
0
0
2
1 0 0
0 1 0
2E
2
0 0 1
Дисперсійно коваріаційна матриця випадкових
величин ui . По діагоналі її стоять дисперсії, поза
діагоналлю коваріації.
7.
Припущення 4. Вектор випадкових величин ui маєнормальний закон розподілу
Припущення 5. Матриця X
утворюється з
фіксованих елементів, тобто не випадкова.
Припущення 6. Між факторами xi , x j відсутня
мультиколінеарність, тобто фактори незалежні між
собою. Це означає, що стовпці матриці X лінійно
незалежні, тобто не знайдеться таких чисел 0 , 1, …,
m , серед яких не всі дорівнюють нулю, щоб
виразити один стовпець як лінійну комбінацію
інших:
0 1 1 x1i ... m xmi 0 або γ X 0 .
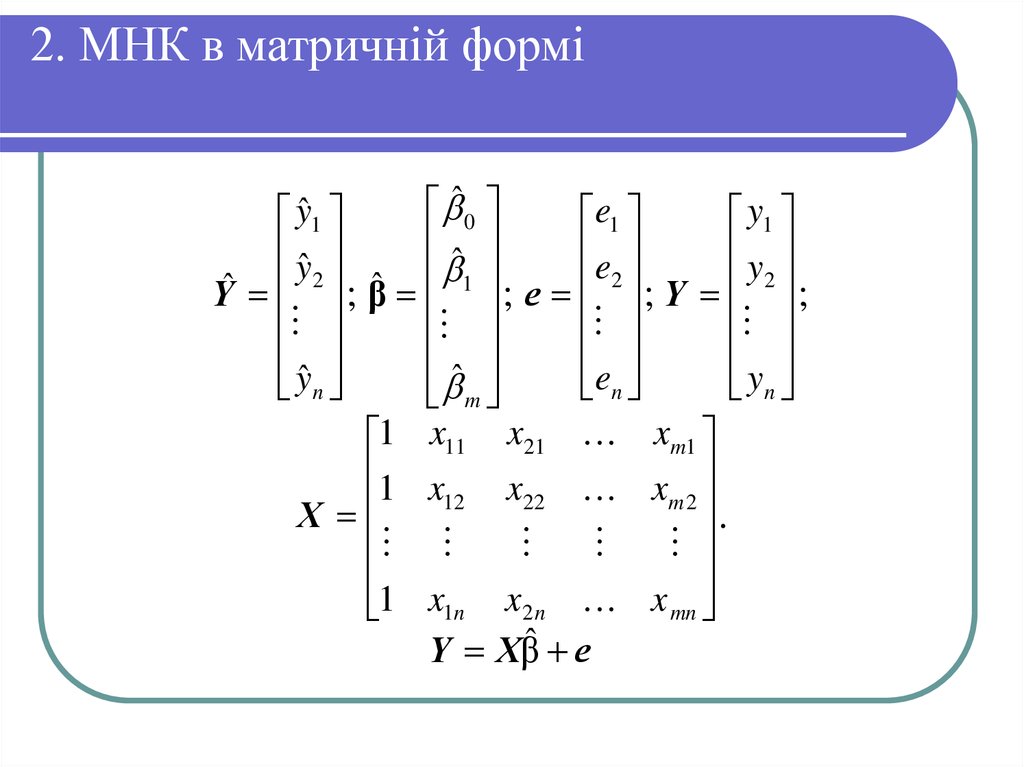
8. 2. МНК в матричній формі
ˆ0yˆ1
e1
y1
yˆ
e
y
ˆ
Yˆ 2 ; βˆ 1 ; e 2 ; Y 2 ;
y
e
y
ˆ
ˆ
n
n
n
m
1 x11 x21 xm1
1 x
x
x
12
22
m2
.
X
1 x
x
x
1n
2n
mn
Y Xβˆ e
9.
ne(βˆ ) ei2 e e (Y - Xβˆ ) (Y - Xβˆ )
i 1
Y Y - 2βˆ X Y βˆ X Xβˆ min
[ ( Xβˆ ) βˆ X ; βˆ X Y Y Xβˆ ].
e(βˆ )
2 X Y 2 X Xβˆ 0.
βˆ
X Xβˆ X Y
βˆ ( X X ) 1 X Y
(Символ штрих ( ) означає операцію
транспонування)
10. 3. Дисперсійно-коваріаційна матриця
M [(βˆ β) (βˆ β) ]M ( ˆ 0 0 ) 2
M ( ˆ 0 0 )( ˆ 1 1 )
ˆ 1 1 )( ˆ 0 0 )
ˆ 1 1 ) 2
M
(
M
(
ˆ
M ( m m )( ˆ 0 0 ) M ( ˆ m m )( ˆ 1 1 )
M ( ˆ 0 0 )( ˆ m m )
M ( ˆ 1 1 )( ˆ m m )
M ( ˆ m m ) 2
11.
2ˆˆ0 ˆ1 ˆ0 ˆm
0
2
ˆ ˆ
ˆ1
ˆ1 ˆm
1 0
.
2
ˆm ˆ0 ˆm ˆ1 ˆm
var(βˆ ) ˆ u2 ( X X ) 1
де ˆ u2 оцінена дисперсія випадкової величини:
n
ˆ u2
2
e
i
i 1
n m 1
Y Y - βˆ X Y
e e
2
ˆ u
.
n m 1
n m 1
12. 4. Прогнозування за економетричною моделлю
H 0 : 0 1 m 0.H1 : не всі j ( j 0, m) дорівнюють нулю.
F відношення з m та n m 1
ступенями вільності:
13.
n2
(
y
y
)
ˆ
i
n
i 1
F
m
n
2
(
y
y
)
i ˆi
i 1
(n m 1) ( yˆ i y ) 2
i 1
n
m ( yi yˆ i ) 2
,
i 1
n m 1
де m кількість факторів, що ввійшли в модель, n
кількість спостережень у вибірці.
(n m 1) R 2
F
m(1 R 2 )
Fкр (m; n m 1; )
14.
Якщо F Fкр , то ми відкидаємо H 0 з ризикомпомилитися не більше ніж в % випадків, і
приймаємо,
що
побудоване
рівняння
економетричної
моделі
адекватне
реальній
дійсності.
Якщо F Fкр H 0 приймаємо і вважаємо, що
побудована модель неадекватна. Тоді необхідно,
можливо, будувати нелінійну модель або ввести
додаткові фактори.
15.
Точковий прогноз:yˆ n k ˆ0 ˆ1 x1,n k ... ˆm xm,n k
або в матричній формі:
Yˆn k X n k βˆ ,
де X n k матриця очікуваних пояснювальних
змінних.
Інтервал, у який з певною заданою імовірністю
p 1 потрапляє дійсне значення залежної
змінної:
Yˆn k t ˆ u 1 X n k ( X X ) -1 X n k ,
k вектор значень з m факторів у період n k .
де X n
Yˆn k t ˆ u X n k ( X X ) -1 X n k .














 mathematics
mathematics








