Кореляційний та регресійний аналіз

1.

КОРЕЛЯЦІЙНИЙ ТА
РЕГРЕСІЙНИЙ
АНАЛІЗ
1

2. Кореляційний аналіз

• Кореляційний аналіз – це статистичне
дослідження (стохастичної) залежності
між випадковими величинами
• У найпростішому випадку досліджують
дві вибірки (набори даних), у
загальному – багатовимірні комплекси
(групи) біомедичних параметрів або
об’єктів.

3. Кореляційний аналіз

• Головні завдання кореляційного аналізу:
– 1) оцінка за вибірковими даними коефіцієнтів
кореляції;
– 2) перевірка значущості вибіркових
коефіцієнтів кореляції або кореляційного
відношення;
– 3) оцінка близькості виявленого зв’язку до
лінійного;
– 4) побудова довірчого інтервалу для
коефіцієнтів кореляції.

4. Кореляційний аналіз

• Парна кореляція
– Найпростіша для дослідження парна кореляція, решту
побудована на її основі. Парний коефіцієнт кореляції
стосується лінійної моделі зв’язку між даними, у
складніших випадках досліджують нелінійну
кореляцію, а мірою нелінійного зв’язку є кореляційне
відношення. Якщо існує лінійний зв’язок, то він буде
виявлений і як нелінійна кореляція. Навпаки, існування
зв’язку взагалі не є підставою стверджувати про
наявність лінійного зв’язку. Отже, нелінійна
кореляція – сильніша властивість, а лінійна кореляція є
частковим випадком нелінійної кореляції (або
кореляції в загальному випадку).

5. Кореляційний аналіз

Властивості коефіцієнта кореляції
1. Коефіцієнт кореляції є в межах від -1 до +1.
.
Якщо (x, y) > 0, то кореляція пряма, а якщо (x, y) <
0 – зворотна. Пряма кореляція: більшим значенням
випадкової змінної x відповідають більші значення y;
зворотна кореляція: більшим значенням x
відповідають менші y і навпаки, більшим y – менші x.
2. Симетрія
(x, y) = (y, x) .

6. Кореляційний аналіз

3. Якщо x та y пов’язані лінійним функціональним
зв’язком y(x) = a + bx, a і b – сталі, то
навпаки .
,і
4. Якщо випадкові змінні лінійно незалежні, то (x, y) = 0,
і навпаки.
Останні дві властивості можна сформулювати як
необхідну й достатню умови, причому критерієм
залежності випадкових величин x і y є відмінність
коефіцієнта кореляції від нуля:
.

7. Кореляційний аналіз

Вибірковий коефіцієнт кореляції
Розрізняють істинний коефіцієнт кореляції (x, y) та його
оцінку за вибіркою r(x, y) < 0, що є випадковим числом.
Вибірковий коефіцієнт кореляції знаходять за формулою
.

8. Кореляційний аналіз

Для малого обсягу даних значення r буде заниженим
порівняно з істинним коефіцієнтом кореляції . Тому
для n < 10 рекомендують використовувати уточнену
оцінку
.

9. Кореляційний аналіз

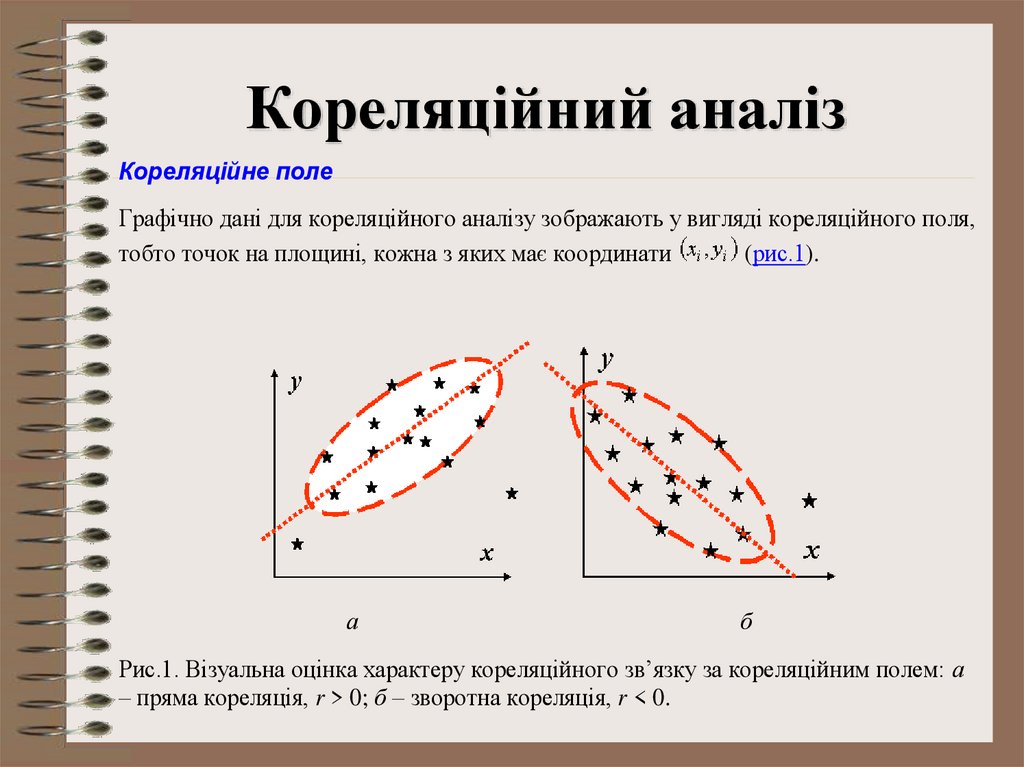
Кореляційне поле
Графічно дані для кореляційного аналізу зображають у вигляді кореляційного поля,
тобто точок на площині, кожна з яких має координати
(рис.1).
а
б
Рис.1. Візуальна оцінка характеру кореляційного зв’язку за кореляційним полем: а
– пряма кореляція, r > 0; б – зворотна кореляція, r < 0.

10. Кореляційний аналіз

Для прямої кореляції характерною тенденцією є
збільшення одного з параметрів, якщо збільшується
інший, а для оберненої, навпаки: збільшення одного
супроводжується, як звичайно, зменшенням іншого.
Причиною фіктивної кореляції (тобто такої, що
спостережена, але не властива природним об’єктам)
може бути неоднорідність сукупності даних, які
відображають два різні об’єкти (рис. 2). Іноді методика
дослідження впливає на створення видимості зв’язку
там, де його немає. Наприклад, якщо при
електронномікроскопічному дослідженні вимірювати
довжину і ширину без урахування орієнтації клітин, то
всі точки кореляційного поля лежатимуть у секторі
від 0 до 45° (замість сектора 0–90°), що помилково
можна сприйняти як наявність деякого зв’язку (рис. 3).

11. Кореляційний аналіз

Рис. 2. Некорельовані дані, r = 0 і фіктивна кореляція (неоднорідні
дані).

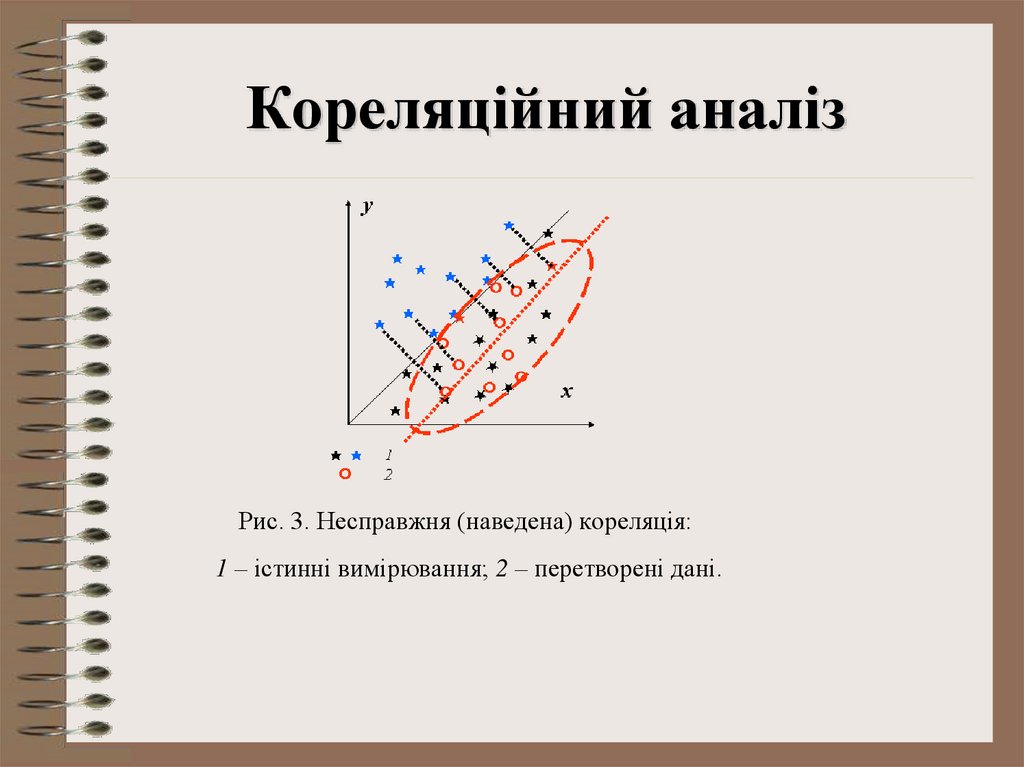
12. Кореляційний аналіз

Рис. 3. Несправжня (наведена) кореляція:
1 – істинні вимірювання; 2 – перетворені дані.

13. Кореляційний аналіз

Перевірка гіпотези про значущість коефіцієнта кореляції
Згідно зі схемою статистичного доведення виконуємо таке.
1. Нульова гіпотеза: лінійного зв’язку немає, тоді істинний коефіцієнт
кореляції дорівнює нулю:
:
за двосторонньої альтернативи
:
2. Вибираємо
.
, наприклад,
.
3. Обчислюємо вибірковий коефіцієнт кореляції r і будуємо статистику
.
)

14. Кореляційний аналіз

Ця статистика має розподіл Стьюдента з
ступенями вільності, а для n > 60 можна використовувати
й стандартний закон розподілу.
Знаходимо критичні значення статистики, тобто квантилі
розподілу Стьюдента (чи стандартного для великих
вибірок) для заданого рівня значущості . Для
маємо
,

15. Кореляційний аналіз

для n > 60 – наближену формулу
,
де
закону розподілу.
– обернена функція стандартного
Перевіряємо критерій: якщо
, то нульову
гіпотезу відхиляємо, тобто існує суттєвий лінійний
зв’язок між даними (дані корелюють).

16. Кореляційний аналіз

На практиці зручнішою є формула, яка дає критичне значення
самого коефіцієнта кореляції. З рівняння статистики можна
визначити
.
Ця формула дає змогу один раз відшукати критичне значення
коефіцієнта кореляції (для фіксованого і n) і використовувати
його в наступній серії порівнянь парних коефіцієнтів кореляції
з критичним, наприклад, для перевірки на значущість
коефіцієнтів кореляційної матриці.

17. Кореляційний аналіз

Вибірковий коефіцієнт кореляції
Розрізняють істинний коефіцієнт кореляції (x, y) та
його оцінку за вибіркою r(x, y) < 0, що є випадковим
числом. Вибірковий коефіцієнт кореляції знаходять
за формулою
.

18. Кореляційний аналіз

Вибірковий коефіцієнт кореляції
Для малого обсягу даних значення r буде заниженим
порівняно з істинним коефіцієнтом кореляції .
Тому для n < 10 рекомендують використовувати
уточнену оцінку
.

19. РОЗРАХУНОК ПРЯМИХ РЕГРЕСІЙ

Формули виправлених дисперсій s2 :
n
1
s1
( xi x в )
n 1 i 1
2
2
s 22
n
1
( yi y в )
n 1 i 1
2
(9)
Оцінкою для служить величина
1 n
в
( x i x в )( y i y в )
n - 1 i 1
( 10 )
19

20. ПЕРЕВІРКА ЗНАЧУСТОСТІ ВИБІРКОВОГО КОЕФІЦІЄНТА КОРЕЛЯЦІЇ

На практиці для оцінки тісноти
лінійного
кореляційного
зв'язку
використовують вибірковий коефіцієнт
кореляції,
який
визначається
за
формулою:
r 2 2
( 11 )
s1 s 2
20

21. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

Метод найменших квадратів служить
для оцінки невідомих величин за
результатами вимірювань, які містять
випадкові похибки. Серед багатьох
застосовувань
цього
методу
найважливішим є знаходження рівняння,
яке найбільш точно описує дану
залежність для подання дослідних
результатів.
21

22. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

Процес практичного використання цього
методу складається з двох етапів: на першому
вибирають вид шуканої формули, а на другому
підбирають для неї параметри.
Нехай задано експериментальні дані, для яких
за емпіричну формулу можна прийняти лінійну
залежність y = ax + b та квадратичну y = ax2 +bx
+c
Згідно з ідеєю методу найменших квадратів
потрібно мінімізувати суму
22

23. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

( 12 )
де хі, уі - значення дослідних даних;
- значення функції, взяте на
емпіричній залежності в точці хі
п – число дослідів
У випадку лінійної емпіричної формули
сума набуває вигляду:
( 13)
23

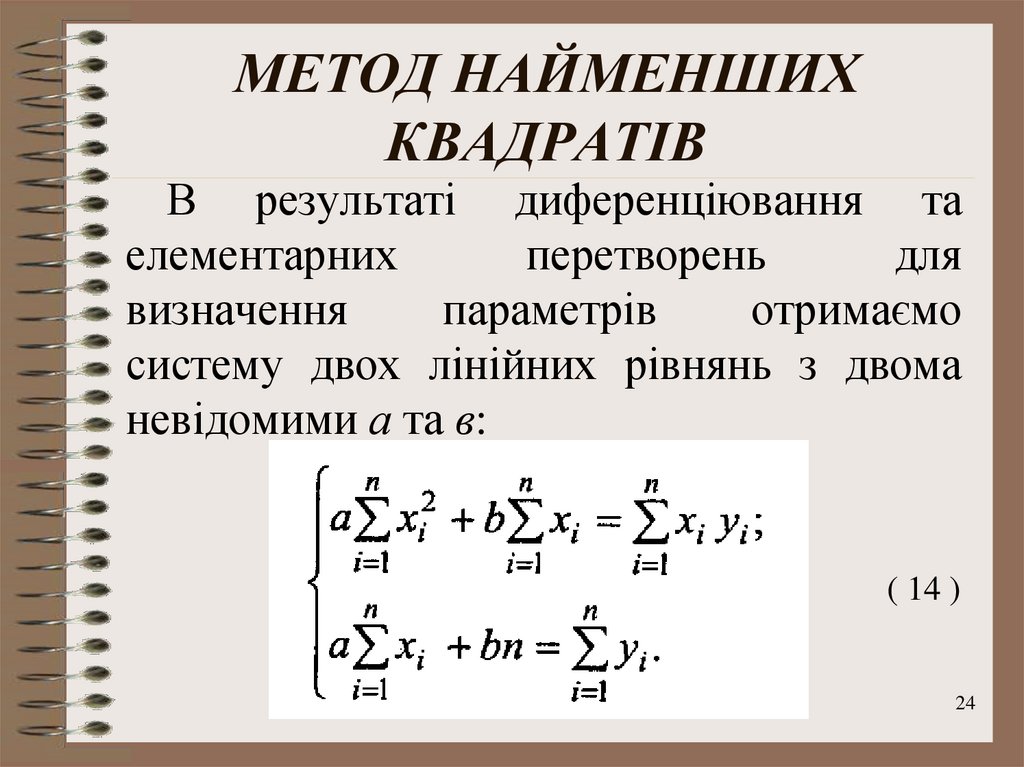
24. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

В результаті диференціювання та
елементарних
перетворень
для
визначення
параметрів
отримаємо
систему двох лінійних рівнянь з двома
невідомими а та в:
( 14 )
24

25. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

У випадку квадратичної залежності
сума
Тоді система буде складатися з трьох
рівнянь з трьома невідомими:
( 15)
25

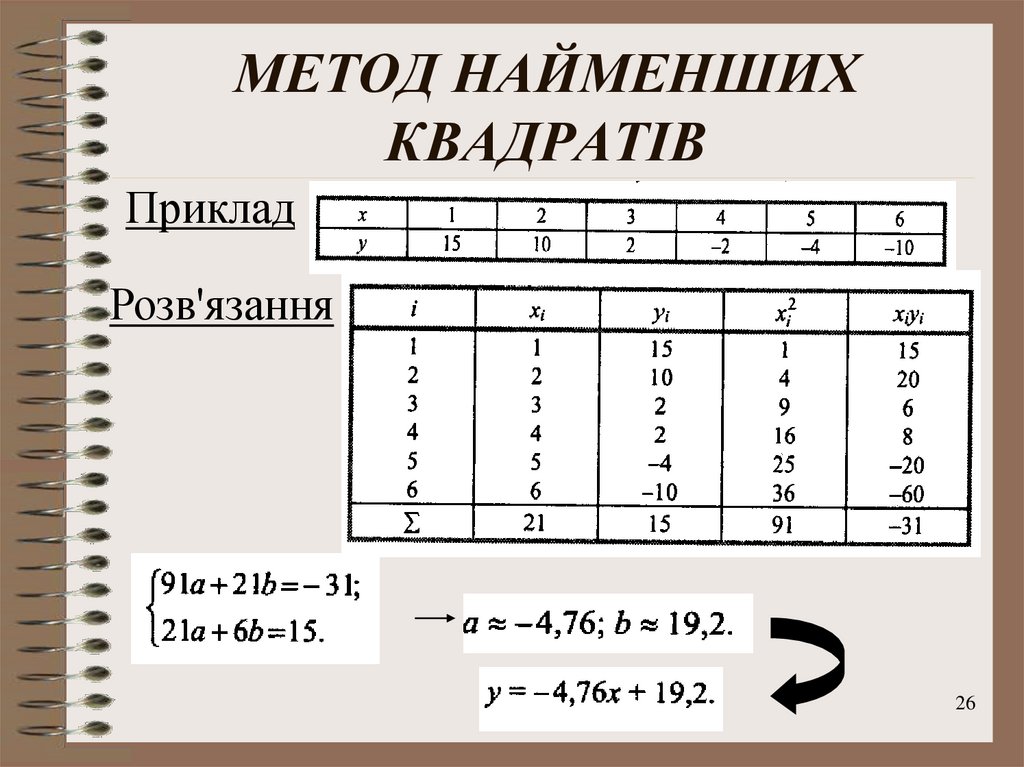
26. МЕТОД НАЙМЕНШИХ КВАДРАТІВ

Приклад
Розв'язання
26