Similar presentations:
Площадь параллелограмма. 8 класс
1.
Площадьпараллелограмма
Геометрия 8 класс
2.
Цели урокаОбучающие цели дать определение высоты параллелограмма ;
доказать теорему о площади параллелограмма;
показать применение формулы в процессе решения задач
Воспитывающие цели вызвать интерес к геометрии;
пробудить интерес к самостоятельному решению задач;
побудить учащихся к активности;
совершенствовать навыки решения задач
Развивающие цели учить сравнивать;
учить выделять главное;
учить строить аналоги
3.
План урока1. Организационный момент
2. Устные упражнения, тест на повторение
3. Задача
4. Объяснение нового материала
5. Решение задач
6. Итог урока
7. Домашнее задание
4.
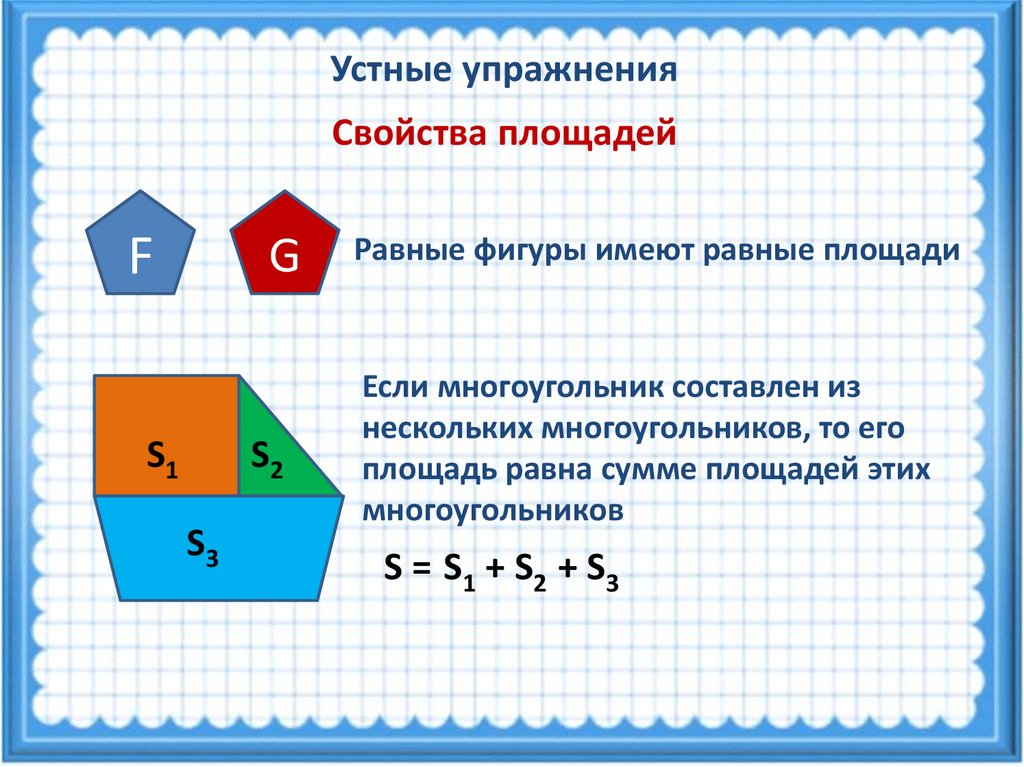
Устные упражненияСвойства площадей
F
G
S1
S2
S3
Равные фигуры имеют равные площади
Если многоугольник составлен из
нескольких многоугольников, то его
площадь равна сумме площадей этих
многоугольников
S = S1 + S2 + S3
5.
Тест на повторение1.Найдите площадь квадрата, если его сторона
равна 8см
1) 16
2) 64
3) 32
S = 82 =64см 2
6.
Тест на повторение2.Найдите периметр квадрата, если
площадь равна 16 см2
1) 64
2) 32
3) 16
а = 4см
Р = 4·4 =16см
7.
Тест на повторение3.Найдите площадь треугольника, если
его катеты равны по 10см
1) 50
2) 25
3) 20
S =10 2:2=50см2
8.
Тест на повторение4.Найдите площадь прямоугольника, если
его смежные стороны равны 10см и 8см
1) 36
2) 40
3) 80
S = 10·8 = 80см2
9.
Тест на повторение5.Найдите площадь треугольника, если
его катеты равны 4см и 8см
S = (4·8):2= 16см2
1) 24
2) 32
8
3) 16
4
10.
Тест на повторение6.Найдите площадь параллелограмма ABCD,
если АН=СК=4см, НD=6см и ВН=DК=8см.
S = 2((4·8):2)+6·8= 80см2
В
1) 48
К
С
4
2) 64
8
3) 80
4
А
8
6
Н
D
11.
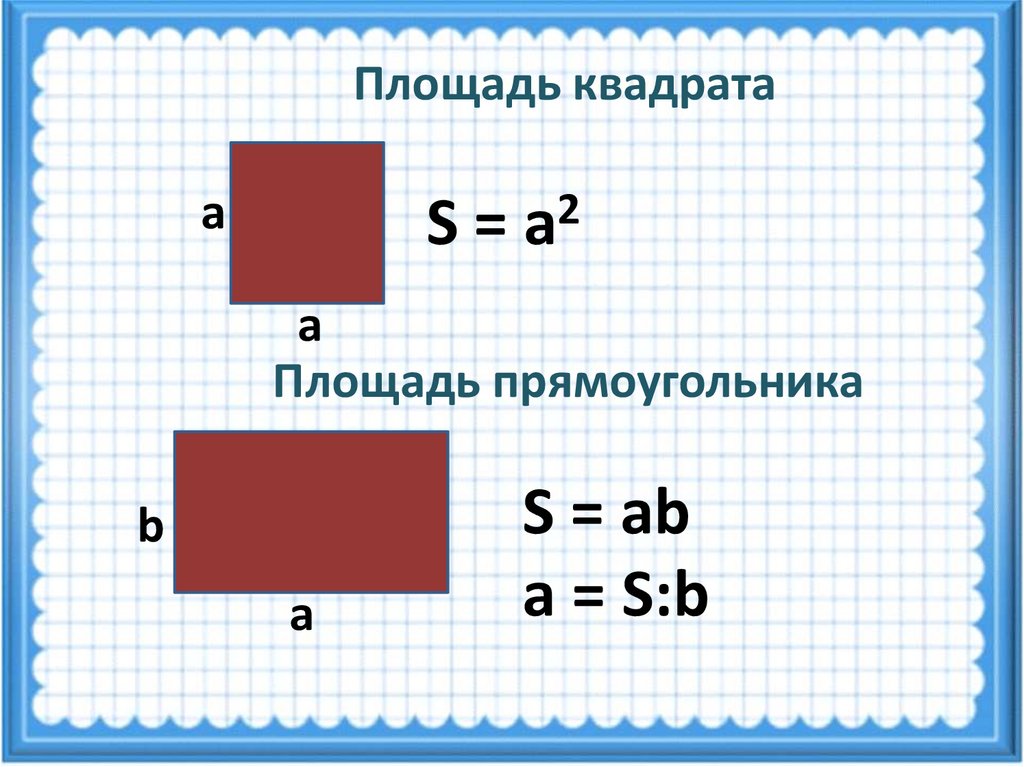
Площадь квадратаa
S=
2
a
a
Площадь прямоугольника
b
a
S = ab
а = S:b
12.
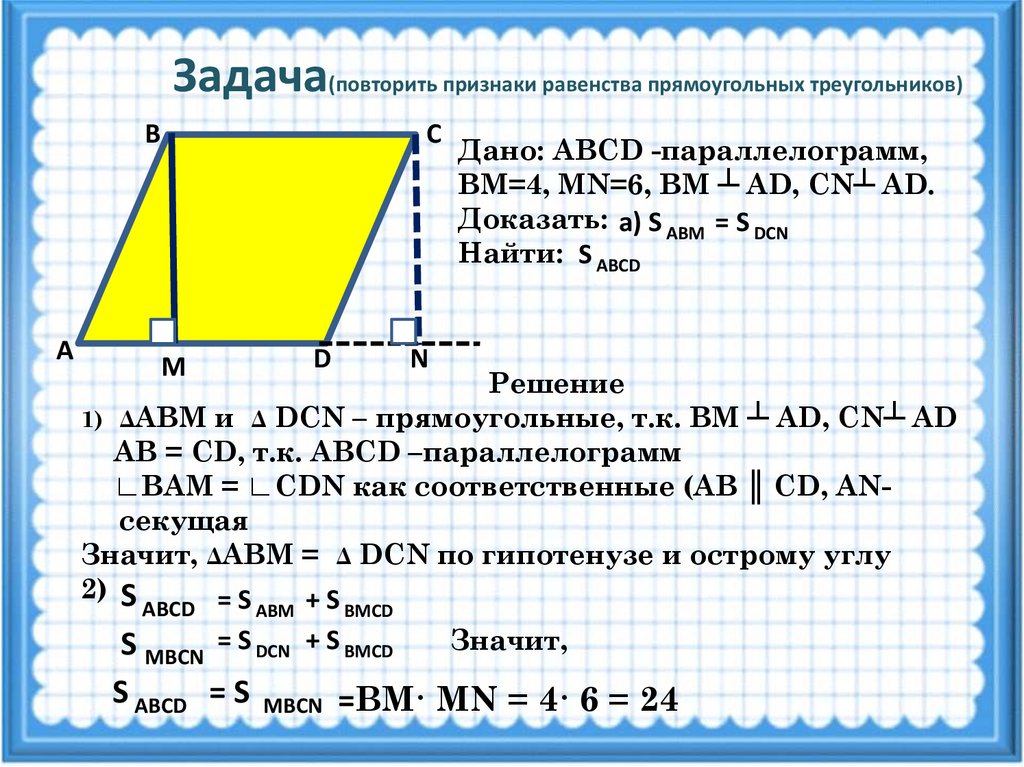
Задача(повторить признаки равенства прямоугольных треугольников)В
А
С
D
M
Дано: ABCD -параллелограмм,
ВМ=4, MN=6, ВМ ┴ AD, CN┴ AD.
Доказать: а) S ABМ = S DCN
Найти: S ABCD
N
Решение
1) ΔАВМ и Δ DCN – прямоугольные, т.к. ВМ ┴ AD, CN┴ AD
AB = CD, т.к. ABCD –параллелограмм
∟ВАМ = ∟CDN как соответственные (AB ║ CD, ANсекущая
Значит, ΔАВМ = Δ DCN по гипотенузе и острому углу
2) S
=S
+S
ABCD
ABМ
BМСD
Значит,
S MBCN = S DCN + S BМСD
S ABCD = S MBCN =ВМ· MN = 4· 6 = 24
13.
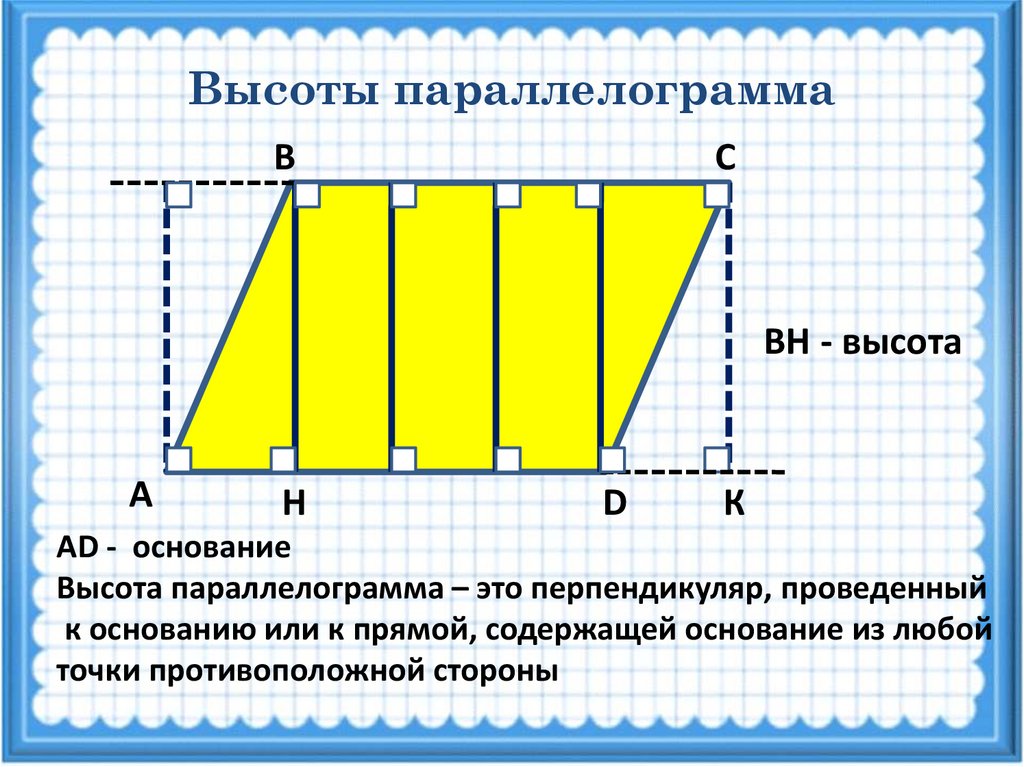
Высоты параллелограммаВ
С
ВН - высота
А
Н
D
К
АD - основание
Высота параллелограмма – это перпендикуляр, проведенный
к основанию или к прямой, содержащей основание из любой
точки противоположной стороны
14.
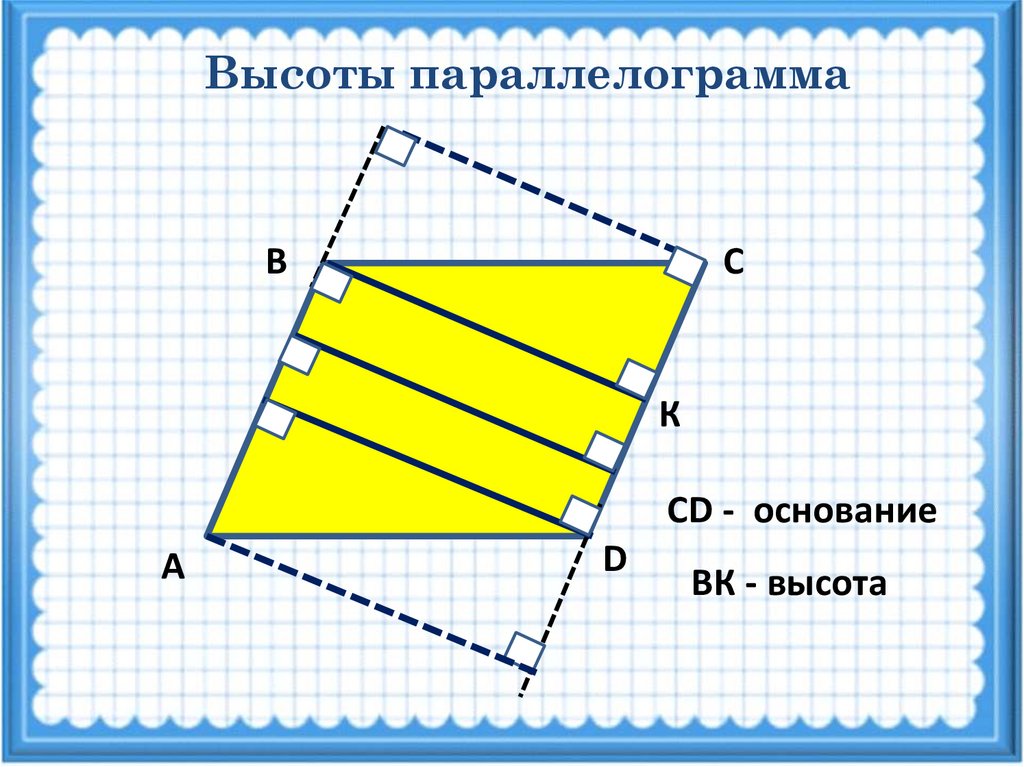
Высоты параллелограммаВ
С
К
СD - основание
А
D
ВК - высота
15.
Площадь параллелограммаТ Площадь параллелограмма равна
произведению его основания на
высоту.
16.
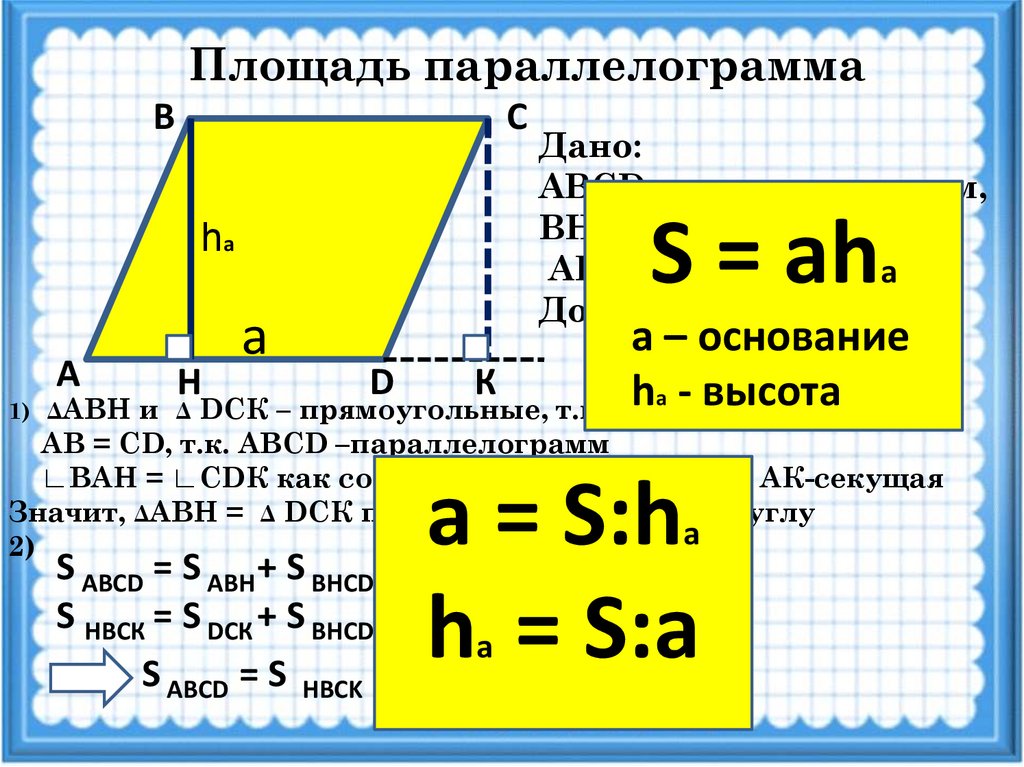
Площадь параллелограммаВ
С
S = ah
hа
А
1) ΔАВН
Дано:
ABCD -параллелограмм,
ВН - высота
AD - основание
а
Доказать: S = AD·BH
a
а – основание
Док-во:
Н
D
К
hа - высота
Δ DCК – прямоугольные, т.к. ВН ┴ AD, CК ┴ AD
и
AB = CD, т.к. ABCD –параллелограмм
∟ВАН = ∟CDК как соответственные (AB ║ CD, AК-секущая
Значит, ΔАВН = Δ DCК по гипотенузе и острому углу
а
2)
а = S:h
h = S:а
S ABCD = S ABН + S BНСD
S НBCК = S DCК + S BНСD
а
S ABCD = S HBCK = ВС·ВН = AD·ВН
17.
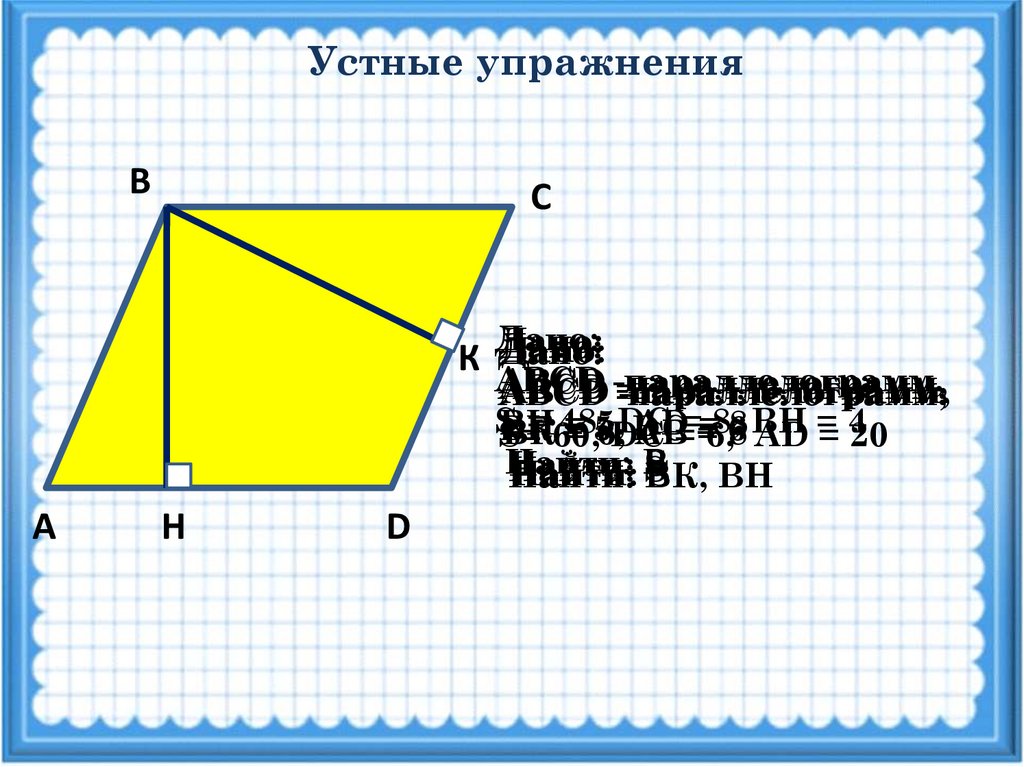
Устные упражненияВ
С
Дано:
Дано:
К Дано:
ABCD
ABCD
-параллелограмм,
ABCD -параллелограмм,
-параллелограмм,
S
= 60,
48,
DC
8,6
ВН
=
АD
=6,
8 ВН
ВК
DC
= 5,
6,DC
АВ===
8
S=
АD =
=4
20
Найти:
Найти: Р
S
S ВН
Найти:
ВК,
А
Н
D
18.
Закрепление изученного материала№461
19.
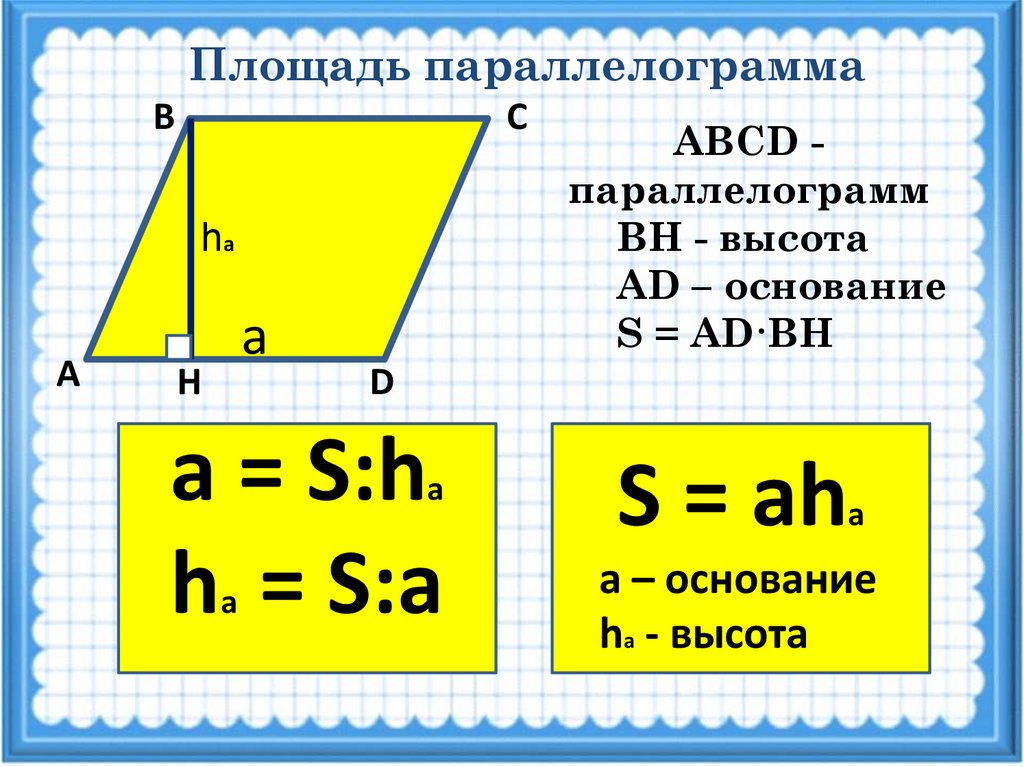
Площадь параллелограммаВ
С
hа
А
a
Н
D
а = S:h
h = S:а
а
а
ABCD параллелограмм
ВН - высота
AD – основание
S = AD·BH
S = ah
а
а – основание
hа - высота
20.
Домашнее заданиеп. 51, №460, №462.
21.
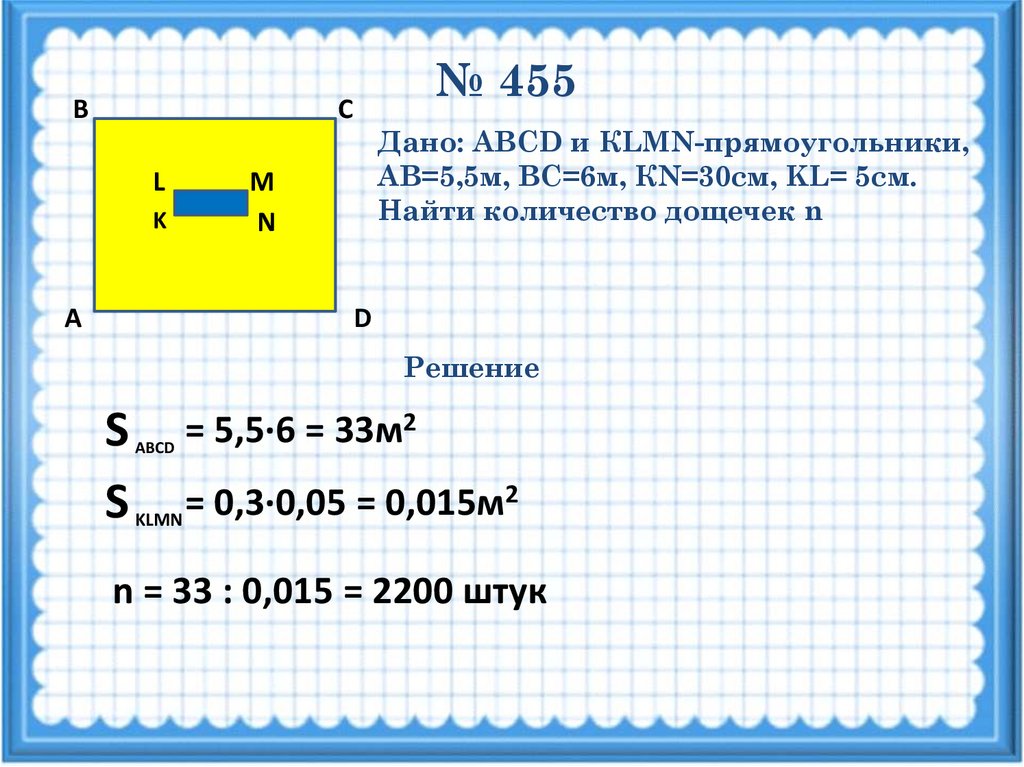
В№ 455
С
L
K
А
Дано: ABCD и КLMN-прямоугольники,
АВ=5,5м, ВС=6м, КN=30см, KL= 5см.
Найти количество дощечек n
M
N
D
Решение
S
S
2
=
5,5·6
=
33м
ABCD
2
=
0,3·0,05
=
0,015м
KLMN
n = 33 : 0,015 = 2200 штук











 mathematics
mathematics








