Similar presentations:
Системы линейных уравнений СЛУ
1.
3. Системы линейных уравнений СЛУa11 x1
a x
21 1
...
an1 x1
... a1m
a12 x2 ... a1m xm b1
a22 x2 ... a2 m xm b2
..
...
...
AX B
an 2 x2 ... anm xm bn
a11 a12
x1
a a ... a
x
2m
A 21 22
, n m X 2 , m 1
... .. ... ...
...
a
a
...
a
nm
n1 n 2
xm
b1
b
B 2 , n 1
...
bn
3.1. Решение квадратных систем линейных уравнений
(n=m, detA<>0).
3.1.1. C помощью обратной матрицы
1
1
1
AX B A AX A B X A B
2.
3.1.2. Метод КрамераИз предыдущего имеем:
A11 A21
A A
1 12 22
1
X A B
det A ... ..
A1n A2 n
... An1 b1
... An 2 b2
... ... ...
... Ann bn
1
xi
b1 A1i b2 A2i ... bn Ani
det A
1
1 i
2 i
n i
( 1) b1M 1i ( 1) b2 M 2i ... ( 1) bn M ni
det A
a11
a12
...b1
1 a21
det A ...
an1
a22
...b2 ... a2 n
...
i
... ...
det A
...
an 2 ...bn
i
... a1n
... ann
AX B
i
xi
,
det A
i 1, n
3.
3.1.3. Метод Гауссаa11 x1
a x
21 1
A B
...
an1 x1
aa1211x2 a...12 ...
a1m xam 1 n bb1 1
aa2221x2 a...22
.....
aan 2 x2 a...
n1
1 a12 a11
0
a22
...
...
an 2
0
1
0
0
...
0
.....
n2
1 a12 a11 ... a1n a11 b1 a11
ai ai1 a1
a...2 m xam 2 n bb22 a1 : a11 a21
a22
... a2 n
b
A B расширенная
матрица 2
i
2,n
...
... ...... ...
...
...
...
...
...
anm xan bbm
a
a
...
a
b
nn n
n2
nn
n
n1
1 a12 a11
... a1n a11 b1 a11
... a2 n
b2 a2 : a22 0
1
...
...
...
...
... ann
bn
an 2
0
0 a13 ... a1n b1
1
1 a23 ... a2 n b2
0
0 a33 ... a3n b3 ...
...
... .. ... ... ...
0
0 an 3 ... ann bn
... a1n a11 b1 a11
... a2 n a22 b2 a22 ai ai 2 a2
i
1,
n; i 2
...
...
...
ann
bn
x1 b1
0 0 ... 0 b1
1 0 ... 0 b2
x2 b2
... .. ... ... ...
...
x b
0 0 ... 1 bn
n n
Последовательно исключаем переменные, используя элементарные
преобразования, пока не приведем матрицу А к диагональному виду
4.
Пример2 3 4 0
2 x 3 y 4 z 0
5
0
6
7
5
x
6
z
7
0 8 9 10
8 y 9 z 10
A11
0
6
8 9
A12
5
6
A13
5 0
0 9
0 8
48
A21
45
A22
40
48
71
45
1
A B 71
40
71
A23
5 18
71 71
18 8
71 71
16 15
71 71
3 4
8 9
2 4
0 9
8
5 A31
3 4
0
18 A32
2 3
0
1й способ
16 A33
0
7
10
6
4
5
0
6 160 96 135 71
0
8
9
18
2
4
5
6
8
2 3
5
2 3
0
15
35 180 145
71
71
126 80 46
71 71
112 150 38
71 71
48 5 18
71 71 71
45
18
8
A 1
71 71 71
40 16 15
71 71 71
5.
Пример (метод Крамера)2 3 4 0
2 x 3 y 4 z 0
5
0
6
7
6 z 7
5 x
0 8 9 10
8
y
9
z
10
0
3
2 3
2й способ 5
0
6 160 96 135 71
0
8
9
4
7 0 6 180 224 189 145
x
10 8 9
2 0 4
5 7 6 126 200 120 46
y
0 10 9
2 3 0
5
z
0
0
7 112 150 38
8 10
4
145
x
x
71
y 46
y
71
38
z z
71
145
4671
71
38
71
6.
3й способПример (метод Гаусса)
2 3 4 0
2 x 3 y 4 z 0
5
0
6
7
6 z 7
5 x
0 8 9 10
8
y
9
z
10
3
1
2
0
2
a1 : 2 5 0 6 7
0 8 9 10
3
18
21
3
1
2
1 08 3 14 3
1 2 2 0
2
0
1 0 2 15 15
3
15
2
15
2
3
a
a
15
a1 1 a22 2
8 8 1414
a2 5a1 0
4 7 a : 15 0 1 8 14
2
0
1
0
1
2
2
15 151515
2
15
1
5
aa3 8a82a
0 8 9 10
0 8 9 10
64
8 14
3
2
0 38
0 00 90 15 171
15
1
5
15
a3 :
1 0 0 145
18 38
21
18 21
1
0
15
71 15 71
18
15
15
a1 a3
14
46
8
38
15
71
0 1 0
0 1 8 14
8
15
71 15 71
15
15 15
a
a
2
15 3
38 38
0 0 1 38
0
0
1
71
71 71
145
71
46
71
38
71
7.
4. Исследование системы линейных уравнений4.1. Виды систем линейных уравнений.
AX B, A n m, X m 1, B n 1
Однородная система ЛУ:
AX 0
Решение системы — любой вектор-столбец X, для которого
выполняется равенство AX=B.
Совместная система ЛУ:
X существует
Определенная система ЛУ: X единственное
Как определить
<= Теорема Кронекера-Капелли
но сначала…
8.
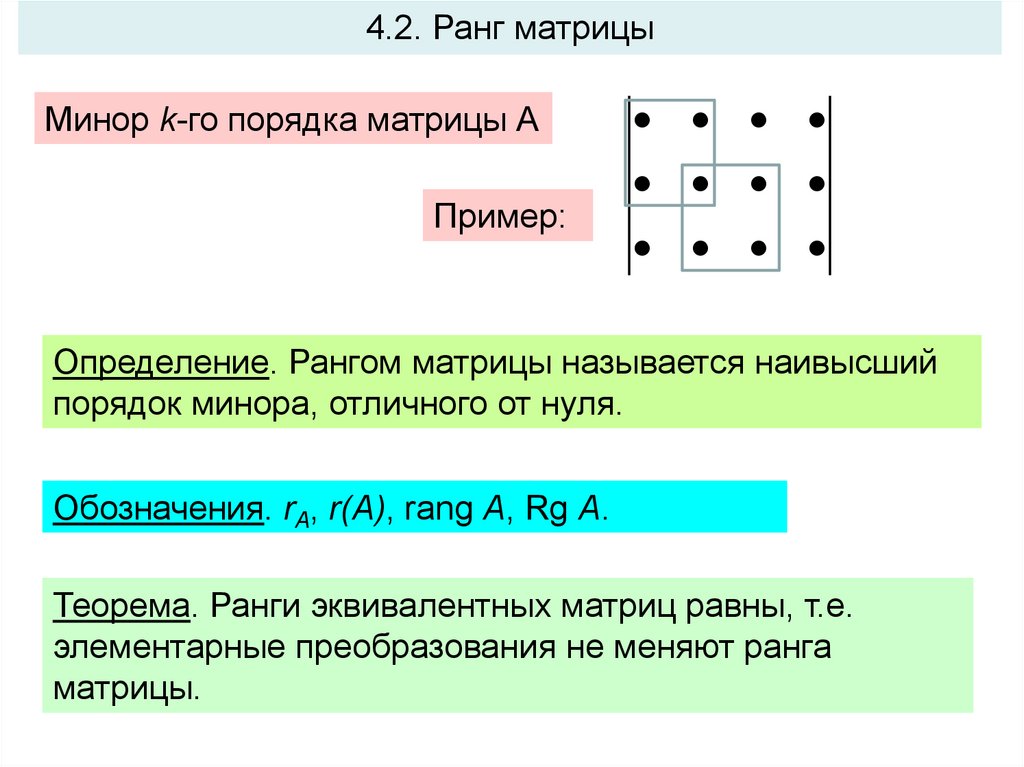
4.2. Ранг матрицыМинор k-го порядка матрицы А
Пример:
Определение. Рангом матрицы называется наивысший
порядок минора, отличного от нуля.
Обозначения. rA, r(A), rang A, Rg A.
Теорема. Ранги эквивалентных матриц равны, т.е.
элементарные преобразования не меняют ранга
матрицы.
9.
Линейная комбинация объектовa1 , a2 ,..., an
1a1 2 a2 ... n an , i R
Объекты линейно зависимы, если существует их
нетривиальная линейная комбинация равная нулю:
1a1 2 a2 ... n an 0, не все i 0
1
0
1
0
0
1 0 1
a1 a2 a3 a4 0 строки линейно зависимы
1 2 0
0 1 1
0 1
Теорема. Ранг матрицы равен наибольшему числу её
линейно независимых строк или столбцов.
10.
r(A)=min{k, l}, гдеk — максимальное число линейно независимых строк А,
l — максимальное число линейно независимых столбцов А.
Следствия для квадратной матрицы.
1. Если определитель квадратной матрицы равен нулю, то
её строки (или столбцы) линейно зависимы.
2. Если строки (или столбцы) квадратной матрицы
линейно зависимы, то её определитель равен нулю.
Способы вычисления ранга матрицы.
1. Метод окаймляющих миноров.
2. Метод элементарных преобразований.
11.
Метод элементарных преобразований.1. С помощью элементарных преобразований получить в левом
верхней углу единичную (или треугольную) матрицу.
2. Нулевые строки переставлять вниз, а нулевые столбцы вправо.
3. Ранг матрицы равен порядку полученной единичной или
треугольной матрицы.
3
1
2
0
4
a
:3
Пример:
A 2 5 3 2 a4 : 2
4 11 9 2
a2 2a1 1 2 0 2 a1 2a2
0 1 1 3
a4 4a1
a3 3a1
0 3 3 9
1 2 0 2
2 5 1 1
4 11 3 1
1 0 2 8
0 1 1 3
0 0 0 0
12.
4.3. Теорема Кронекера-КапеллиПусть АХ=В некоторая СЛУ, A-nxm тогда
1) Если r(A)=r(A|B), то система совместная
Нет строк типа 0=5
1а) Если r(A)=r(A|B)=m, то система совместная и определенная
Сколько неизвестных, столько и разных уравнений => решение единственное
1б) Если r(A)=r(A|B)<m, то с-ма совместная и неопределенная
Неизвестных больше, чем уравнений => решение общее, зависит от С
2) Если r(A)<r(A|B), то система несовместная
ЕСТЬ строки типа 0=5
13.
Замечания об однородной системе AX = 0.1. Она всегда совместна (всегда есть нулевое решение).
2. Нулевое решение существует, только если r(A) < n, или
det A = 0.
Порядок исследования системы линейных уравнений.
1. Исследование совместности:
(а) однородная - неоднородная?
(б) теорема Кронекера-Капелли.
2. Исследование неопределённости:
(а) r(A) = n?
14.
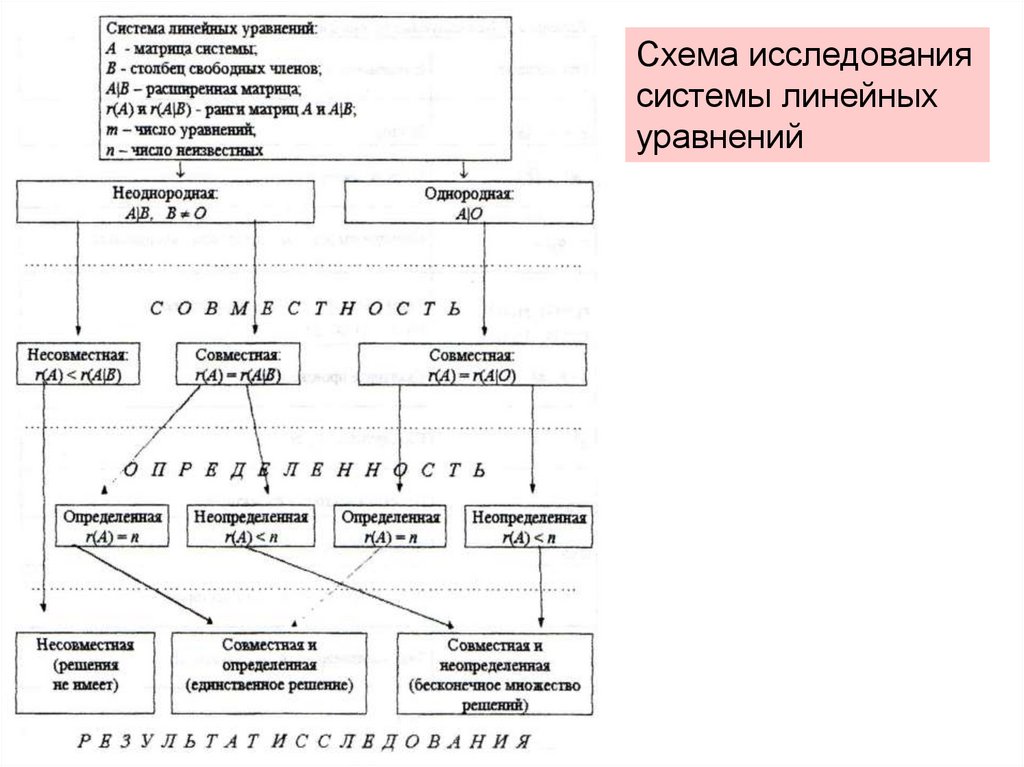
Схема исследованиясистемы линейных
уравнений
15.
Пример1
1
x y z 4
2 x y 3 z 2
4 x 4 y 4 z 20
Проверяем на
совместность.
Если совместна,
то решаем
a2 2a1
1 4 a4 / 4 1 1 1 4
1 1 1 4
a3 a1
2 1 3 2 2 1 3 2
0 3 1 10
4 4 4 20
1 1 1 5
0 0 0 1
r(A) = 2, r(A|B) = 3, r(A) ≠ r(A|B) => система несовместна и
решения не имеет.
16.
Ещё пример1
1
1 4
2 1 3 2
4
4
0 20
x y z 4
2 x y 3 z 2
4 x 4 y
20
a2 2a1
1 1 1 4
a4 / 4 1 1 1 4
a3 a1
0 3 1 10
2 1 3 2
1 1 0 5
0 0 1 1
r(A) = 3, r(A|B) = 3, n = 3 => система совместная и
определённая. Продолжаем…
1 1
1
4
1 0
4/3 2/3
1 0 0 2
0 1 1/ 3 10 / 3 0 1 1/ 3 10 / 3 0 1 0 3
0 0
1 1
0 0
1 1
0 0 1 1
(2; 3; -1)
17.
x y z 42 x y 3 z 2
3x
4 z 2
И ещё пример
1
1
1 4
1
0
1 4
0 3 1 10
0 3 1 10
2 1 3 2
3
1
4 2
1
1
1 4
0 3 1 10
0
0
0 0
r(A) = 2, r(A|B) = 2, n = 3 => система совместная и
неопределённая. Продолжаем…
1 1
1
4
0 1 1/ 3 10 / 3
1 0
4/3 2/3
0 1 1/ 3 10 / 3
x = 2/3-4/3z, y = 10/3+1/3z















 mathematics
mathematics








