Similar presentations:
Прямая линия в пространстве. Взаимное расположение прямой и плоскости
1.
2.
3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ3.1 Линии на плоскости и их уравнения
3.2 Прямая линия на плоскости
3.3 Кривые второго порядка
3.4 Уравнение поверхности и уравнения линии в
пространстве
3.5 Плоскость
3.6 Прямая линия в пространстве
3.7 Взаимное расположение прямой и плоскости
3.
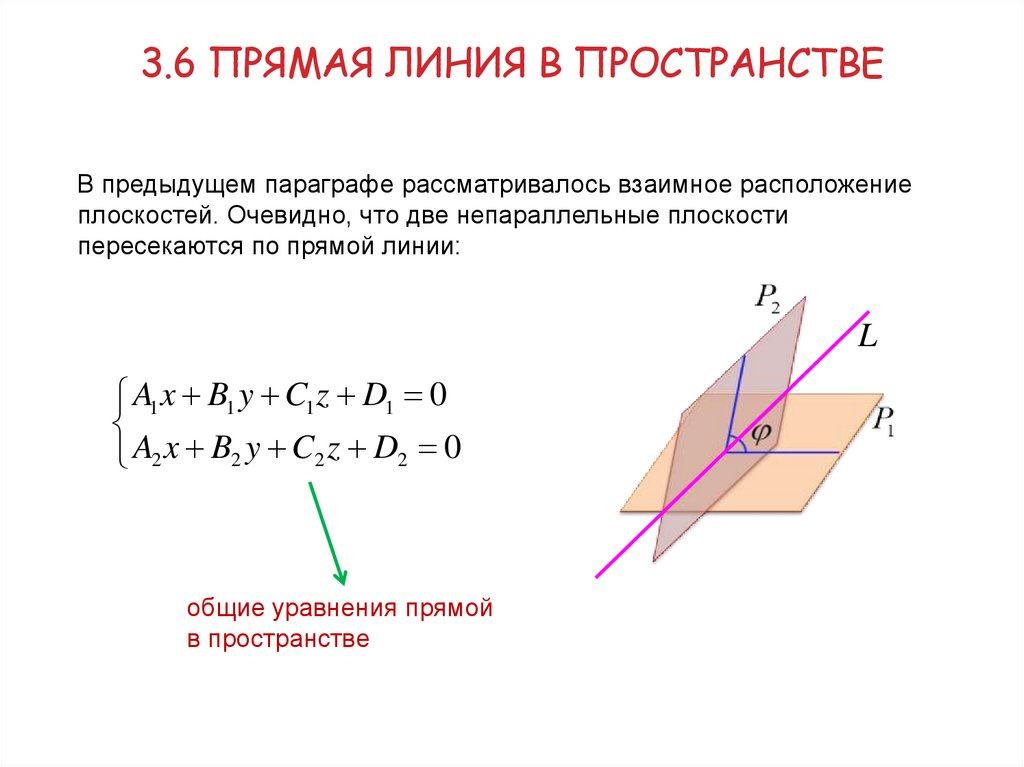
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕВ предыдущем параграфе рассматривалось взаимное расположение
плоскостей. Очевидно, что две непараллельные плоскости
пересекаются по прямой линии:
L
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
общие уравнения прямой
в пространстве
4.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕЗадача 1
z
s
Вывести уравнения прямой L, проходящей через
заданную точку, параллельно заданному вектору.
M
M0
L
x
O
Пусть
Дано:
y
M x; y; z L
M 0 x0 ; y0 ; z0 L, s sx ; s y ; sz
Найти: L
Решение:
– текущая точка, тогда
M 0 M x x0 ; y y0 ; z z0
их координаты пропорциональны
x x0 y y0 z z0
sx
sy
sz
канонические уравнения прямой
s s x ; s y ; s z
– направляющий вектор
5.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕЗамечание
x x0 y y0 z z0
t
sx
sy
sz
Пусть коэффициент пропорциональности равен t, тогда
x x0
t
sx
y y
0
t
sy
z z
0
t
sz
x x0 t sx
y y0 t s y
z z0 t s z
x x0 t sx
y y0 t s y
z z0 t s z
t ;
параметрические уравнения прямой
6.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕЗадача 2
Вывести уравнения прямой L, проходящей через две
заданные точки.
z
M
M1
L
x
O
M2
Дано:
y
M 1 x1; y1; z1 L, M 2 x2 ; y2 ; z2 L
Найти: L
Решение:
M 1M 2 x2 x1; y2 y1; z2 z1
Пусть
M x; y; z L
– текущая точка, тогда
M 1M x x1; y y1; z z1
их координаты пропорциональны
x x1
y y1
z z1
x2 x1 y2 y1 z2 z1
уравнения прямой, проходящей
через две заданные точки
7.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕx x0 y y0 z z0
sx
sy
sz
Замечание
1
2
sx 0
x x0 y y0 z z0
0
sy
sz
Прямая перпендикулярна оси Oх
sy 0
x x0 y y0 z z0
sx
0
sz
Прямая перпендикулярна оси Оу
sz 0
x x0 y y0 z z0
sx
sy
0
Прямая перпендикулярна оси Оz
s y sz 0
x x0 y y0 z z0
sx
0
0
Прямая параллельна оси Oх
sx sz 0
x x0 y y0 z z0
0
sy
0
Прямая параллельна оси Оу
sx s y 0
x x0 y y0 z z0
0
0
sz
Прямая параллельна оси Оz
8.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕЗамечание
3
y 0
x x0 y z
x y z
или
или
sx
0 0
1 0 0
z 0
x 0
x y y0 z
x y z
или
или
0
sy
0
0 1 0
z 0
x 0
x y z z0
x y z
или
или
0 0
sz
0 0 1
y 0
z
O
x
y
Ось Oх
Ось Оу
Ось Оz
9.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕОбобщение
Мы получили несколько типов (форм записи) уравнений прямой в
пространстве, которые отличаются по внешнему виду:
1) общие уравнения,
2) канонические уравнения,
3) параметрические уравнения,
4) уравнения прямой, проходящей через две точки.
Очевидно, что с помощью алгебраических преобразований можно легко
перейти от одной формы записи к другой.
x x0 y y0 z z0
sx
sy
sz
A1x B1 y C1z D1 0
A2 x B2 y C2 z D2 0
x x1
y y1
z z1
x2 x1 y2 y1 z2 z1
x x0 t sx
y y0 t s y
z z0 t s z
10.
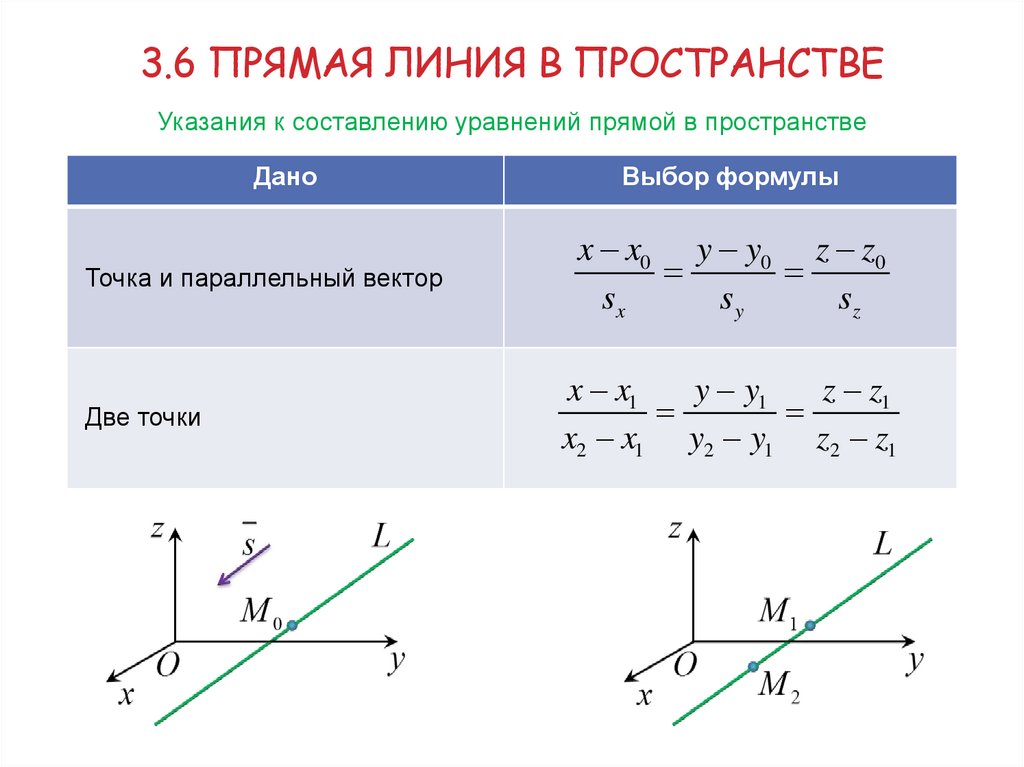
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕУказания к составлению уравнений прямой в пространстве
Дано
Точка и параллельный вектор
Две точки
Выбор формулы
x x0 y y0 z z0
sx
sy
sz
x x1
y y1
z z1
x2 x1 y2 y1 z2 z1
11.
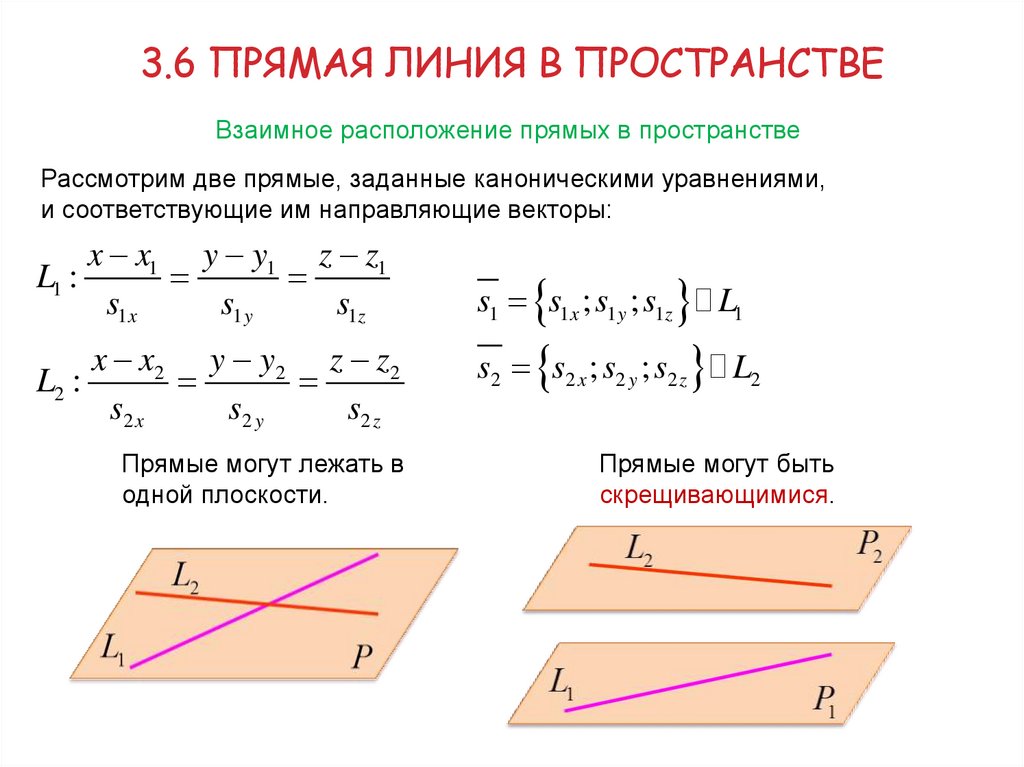
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕВзаимное расположение прямых в пространстве
Рассмотрим две прямые, заданные каноническими уравнениями,
и соответствующие им направляющие векторы:
x x1 y y1 z z1
L1 :
s1x
s1 y
s1z
L2 :
x x2 y y2 z z2
s2 x
s2 y
s2 z
Прямые могут лежать в
одной плоскости.
s1 s1x ; s1 y ; s1z L1
s2 s2 x ; s2 y ; s2 z L2
Прямые могут быть
скрещивающимися.
12.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕВзаимное расположение прямых на плоскости
1
Параллельность прямых
Две параллельные прямые всегда лежат в одной плоскости.
s1x s1 y s1z
s2 x s2 y s2 z
2
Совпадение прямых
К условию параллельности прямых добавляется требование того, что
хотя бы одна точка первой прямой принадлежит второй прямой.
3
Перпендикулярность прямых
Две перпендикулярные прямые могут лежать в одной плоскости или
могут быть скрещивающимися.
L1 L2 s1 s2 s1 s2 0 s1x s2 x s1 y s2 y s1z s2 z 0
13.
3.6 ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕВзаимное расположение прямых на плоскости
4
Угол между прямыми
cos L1; L2 cos s1; s2
L1; L2 arccos
5
s1 s2
s1 s2
s1x s2 x s1 y s2 y s1z s2 z
s12x s12y s12z s22x s22 y s22z
s1x s2 x s1 y s2 y s1z s2 z
s s s s s s
2
1x
2
1y
2
1z
2
2x
2
2y
2
2z
Пересечение прямых
Только для прямых, лежащих в одной плоскости.
x x1 y y1 z z1
s s
s1z
1y
1x
K xk ; yk ; zk :
x x2 y y2 z z2
s2 x
s2 y
s2 z
L2
K
L1
14.
3.7 ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИПусть прямая задана каноническими уравнениями, а плоскость – общим
уравнением.
L:
x x0 y y0 z z0
sx
sy
sz
P : Ax By Cz D 0
1
n A; B; C P
Параллельность прямой и плоскости
s n s n 0 sx A s y B sz C 0
2
Прямая лежит в плоскости
К условию параллельности прямой и плоскости добавляется требование
того, что хотя бы одна точка прямой принадлежит плоскости.
3
Перпендикулярность прямой и плоскости
L P
sx s y sz
A B C
15.
3.7 ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ4
Угол между прямой и плоскостью
s n
sin L; P cos s; n
L; P arcsin
5
s n
sx A s y B sz C
sx2 s y2 sz2 A2 B 2 C 2
sx A s y B sz C
s s s A B C
2
x
2
y
2
z
2
2
2
L
Точка пересечения прямой и плоскости
x x0 y y0 z z0
s s
sz
K xk ; yk ; zk : x
y
Ax By Cz D 0
K
P
16.
Лекция выложена впервые.Если Вы заметили ошибку, то сообщите мне на эл. почту.













 mathematics
mathematics








