Similar presentations:
Определенный интеграл
1. Определенный интеграл
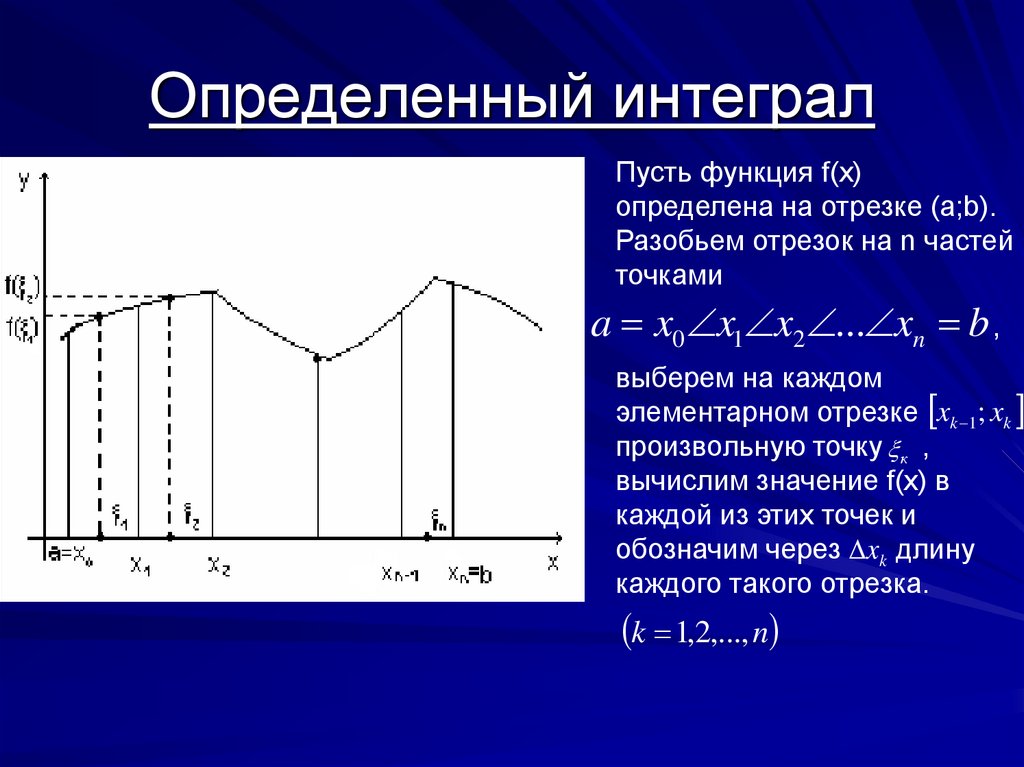
Пусть функция f(x)определена на отрезке (a;b).
Разобьем отрезок на n частей
точками
a x0 x1 x2 ... xn b ,
выберем на каждом
элементарном отрезке xk 1; xk
произвольную точку к ,
вычислим значение f(x) в
каждой из этих точек и
обозначим через xk длину
каждого такого отрезка.
k 1,2,..., n
2.
Определение 1:n
Сумма вида f ( ) x f ( ) x f ( ) x
f ( k ) xk
1
1
2
2
n
n
k 1
называется интегральной суммой для f(x) на отрезке a; b
Определение 2:
Устремим максимальную длину отрезков к нулю. При этом
n . Тогда интегральная сумма стремится к некоторому
b
n
пределу
Lim
f (
max xk 0
k 1
n
k
) xk f ( x)dx
a
называется определенным интегралом от функции f(x) на
отрезке a; b (или в отрезке от a до b). a и b называются
нижним и верхним пределом интегрирования.
3.
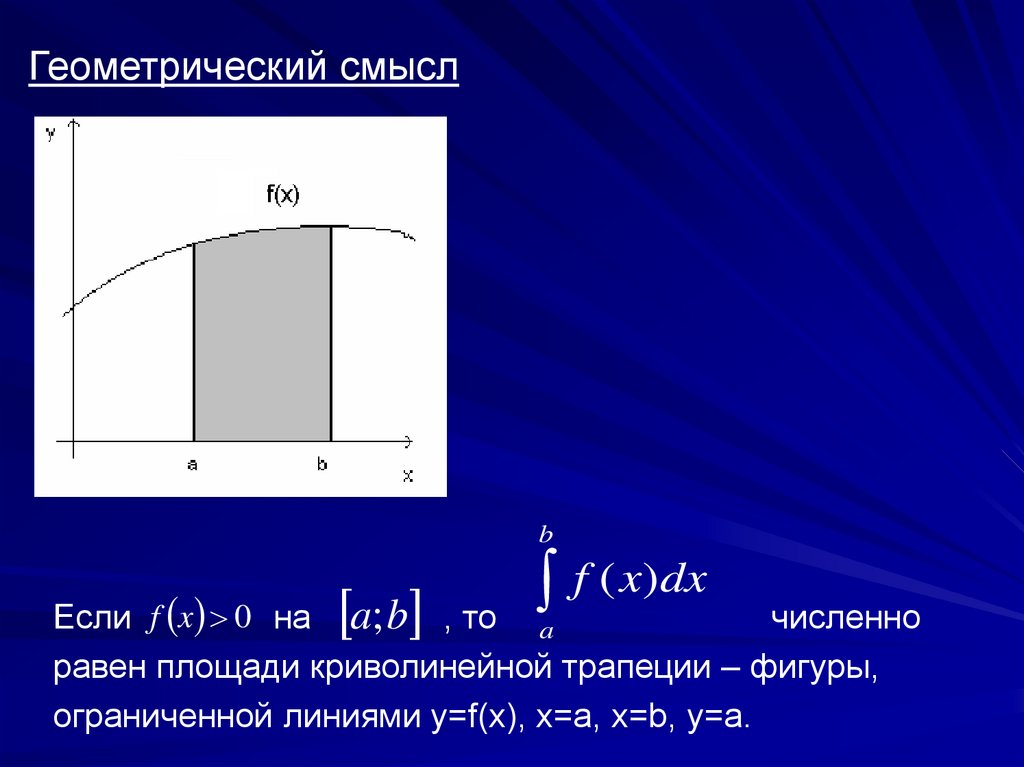
Геометрический смыслb
f ( x)dx
Если f x 0 на a; b , то a
численно
равен площади криволинейной трапеции – фигуры,
ограниченной линиями y=f(x), x=a, x=b, y=a.
4.
Основные свойства определенного интеграла1)Если
f ( x)dx F ( x) C , то
b
f ( x)dx F ( x)
b
a
F (b) F (a)
- формула
a
Ньютона-Лейбница
Здесь F(x) – первообразная для f(x).
b
2)
f ( x) f
1
a
2
b
b
a
a
( x) dx f1 ( x)dx f 2 ( x)dx
5.
3)b
a
a
f ( x)dx f ( x)dx
b
Т.е. при перестановке пределов интегрирования меняется
знак интеграла.
a
4)
f ( x)dx 0
a
Определенный интеграл с одинаковыми пределами
интегрирования равен 0.
6.
5)b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
Т.е. отрезок интегрирования можно разбивать на части.
6)
b
b
a
a
cf
(
x
)
dx
c
f
(
x
)
dx
7.
Примеры2
5
x
dx
4
1.Вычислить
1
2
Найдем первообразную
5x dx 5 x dx 5
4
4
x5
5
1
F ( x) x (C 0)
5
Возьмем
Тогда получаем по формуле Ньютона-Лейбница
2
5x dx x
4
1
5 2
1
2 1 31
5
5
C x5 C
8.
42. Вычислить
(3x e
x
4
)dx
0
Найдем первообразную
x
3 2
4
(3x e )dx 3xdx e dx 2 x 4e C
x
4
x
4
Выберем
x
3 2
4
F ( x) x 4e
2
Тогда
4
x
3 2
3
4
0
4
(
3
x
e
)
dx
(
x
4
e
)
16
4
e
(
0
4
e
) 28 4e
0
0
2
2
x
4







 mathematics
mathematics








