Функция. Область определения и область значений функции

1. Функция. Область определения и область значений функции

18.11.2020
и
Цель обучения: находить область
определения и множество значений функции

2.

Повтори
Определение
Функция - это зависимость у от х
зависимая переменная
независимая переменная
(
)
(
)
Если каждому значению х из некоторого множества чисел
поставлено в соответствие единственное число у ,
то говорят, что на этом множестве задана функция у(х).
у(х)
f
х
y=f(х)

3.

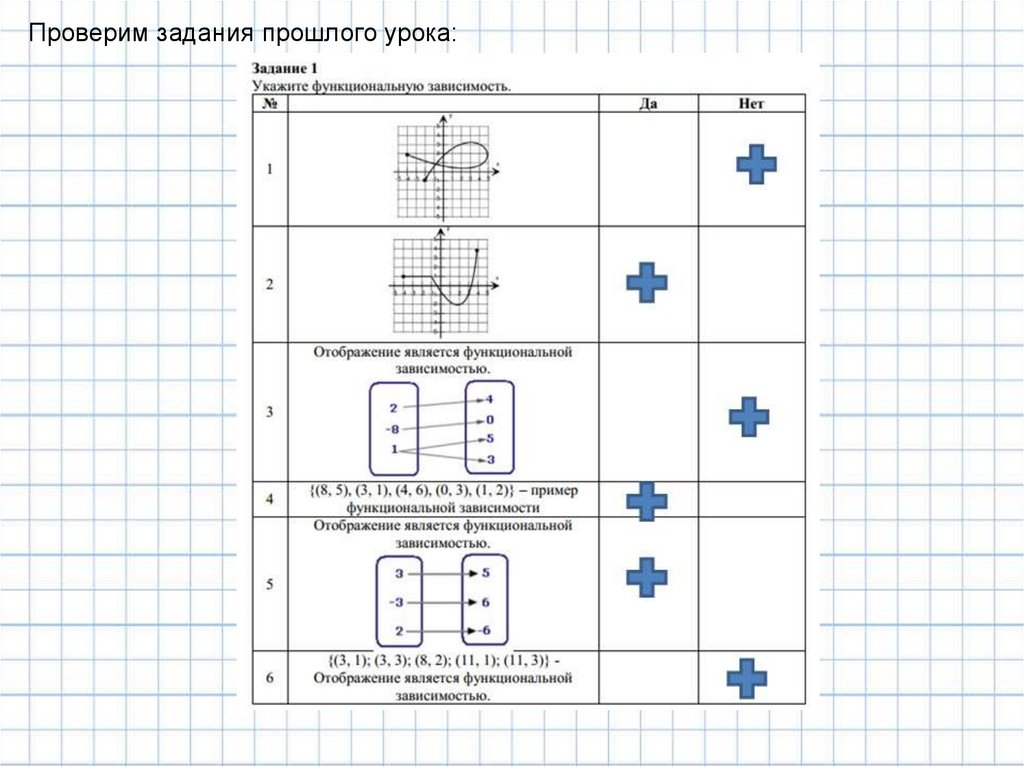
Проверим задания прошлого урока:

4.

Задание 2
i) Турист находится на расстоянии 5 км от города и приближается к нему со скоростью 4
км/ч. На каком расстоянии от города будет турист через 10; 20; 30 мин? Является ли это
расстояние функцией от времени? Задайте ее формулой.
ii) На складе было 600 т угля. Каждый день на склад привозили по 40 т угля. Выразите
формулой количество угля m на складе от времени t. Является ли эта зависимость
функцией?

5.

6.

и
функции
Все значения независимой переменной (все х) образуют
Все значения, которые принимает зависимая переменная
(все у) образуют
y=f(x)
f
х

7.

– это все значения,
которые принимает независимая переменная ( )
Примеры: Найти область определения функций:
1) у =
х2,
1
2)у = х + 2
Если функция задана формулой, то принято считать, что
она
( ), при
которых эта
. В формуле есть
математические действия (+,-,·,:, возведение в степень и
т.д.).
Ограничение в действиях есть только у деления (пока
только это изучено) – на 0 делить нельзя!

8.

– это все значения,
которые принимает независимая переменная ( )
Примеры:
Найти область определения функций –
это найти все значения х :
1) у = х2 – действие возведение в степень,
а в степень возвести можно любое число
значит
–
запишем так:
Это область
определения
Так обозначаем
все действительные
числа
( ; )

9.

– это все значения,
которые принимает независимая переменная ( )
Примеры:
Найти область определения функций:
1
2)у =
х+2
≠
запишем так:

10.

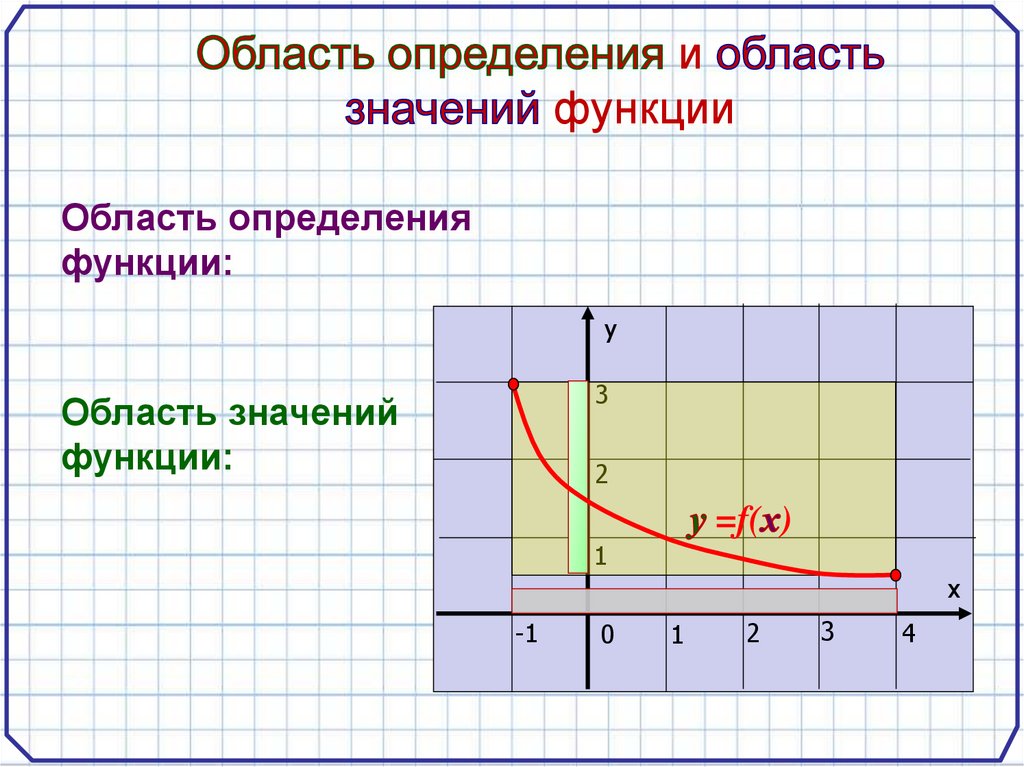
и
функции
Область определения
функции:
у
3
Область значений
функции:
2
=f( )
1
х
-1
0
1
2
3
4

11.

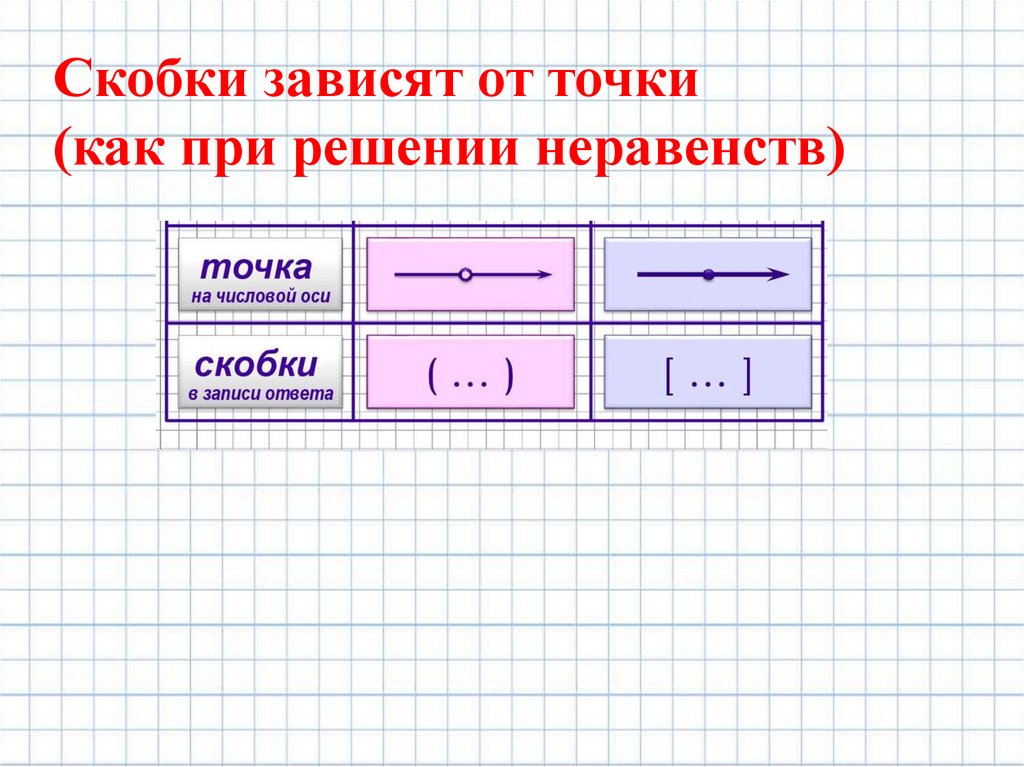
Скобки зависят от точки
(как при решении неравенств)

12.

Выполни учебное задание:
Критерий оценивания Обучающийся
• Находит область определения заданных функций
• Определяет множество значений заданных функций
Уровень мыслительных навыков: Знание и понимание, применение