Similar presentations:
Функция, область определения и область значений функции
1. Домашнее задание
П.47,№1186 (а, б, в),
№1187 (б),
№1188 (г, д)
2.
04.05.2020Функция, область определения и
область значений функции
3. Понятие функции
В тетрадь!Функция – это зависимость переменной
у от переменной х, при которой каждому
значению переменной х соответствует
единственное значение переменной у.
х – независимая переменная или
аргументу
y – зависимая переменная или значение
функции
4. Область определения функции
В тетрадь!Область определения функции
Областью определения функции называют множество
всех значений, которые может принимать ее аргумент х.
Обозначение: D( f )
Область значений функции – все значения зависимой
переменной у.
Обозначение: Е( f )
Если функция у = f(х) задана формулой и ее область
определения не указана, то считают, что область
определения функции состоит из всех значений х, при
которых выражение f(х) имеет смысл.
5. Множество значений функции
В тетрадь!Множество значений функции
Множеством значений функции называют
множество всех значений которые может принимать
переменная у.
Обозначение: Е (у)
6. Способы задания функции:
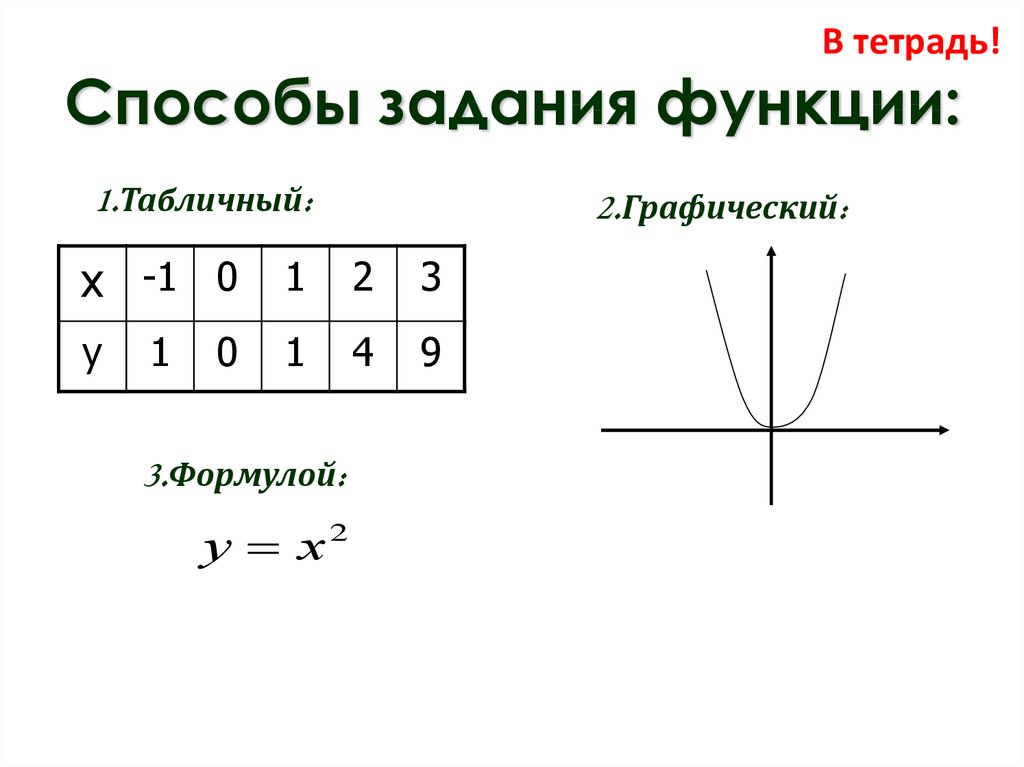
В тетрадь!Способы задания функции:
1.Табличный:
2.Графический:
х -1 0
1
2
3
у
1
4
9
1
0
3.Формулой:
у х
2
7.
№1184x
В тетрадь!
8.
№1186 (г, д, е)В тетрадь!
Значения аргумента, при которых функция у = f(x) обращается в ноль, называют
нулями функции.
приведем к общему
знаменателю
Ответ:
Ответ: 0,5; 2
9.
№1186 (е)В тетрадь!
10.
№1188 (б, в)В тетрадь!
Областью определения функции называют множество всех значений, которые
может принимать ее аргумент х.
Обозначение: D( f )
Функция представлена дробью, аргумент х находиться в
знаменателе. Дробь имеет смысл, если знаменатель ≠ 0.
Т. е мы говорим о допустимых значениях аргумента!
ОДЗ: х – 5 ≠ 0
х≠5
Ответ можно записать разными способами (приветствуется второй способ):
11.
В тетрадь!№1188 (в)
Функция представлена дробью, аргумент х находиться в
знаменателе. Дробь имеет смысл, если знаменатель ≠ 0.
Т. е мы говорим о допустимых значениях аргумента!
используем правила раскрытия модуля
нет таких х при которых
бы выполнялось
неравенство
12.
№1189 (б, г)В тетрадь!
13.
В тетрадь!№1189 (б, г)
2) промежутки, в которых функция принимает только положительные или только
отрицательные значения, называют промежутками знакопостоянства.
| : (-3)
| : (-3)
14.
№1189 (б, г)В тетрадь!
15.
№1189 (г)В тетрадь!














 mathematics
mathematics








