Similar presentations:
Область определения функции
1. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
2. ОПРЕДЕЛЕНИЕ:
Областьопределения
функции – множество
значений, которые
принимает независимая
переменная (х)
3.
у1
х
0
1
4.
у1
х
0
1
5.
у1
х
0
1
6.
у1
х
0
1
7.
у1
х
0
1
8. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
9. ОПРЕДЕЛЕНИЕ:
Областьзначений
функции – множество
значений, которые
принимает функция (f(х))
10.
у1
х
0
1
11.
у1
х
0
1
12.
у1
х
0
1
13.
у1
х
0
1
14.
у1
х
0
1
15. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
16. ОПРЕДЕЛЕНИЕ:
Функция называется четной, если- ее область определения симметрична
относительно начала координат
- выполняется равенство f(-x) = f(x)
Функция называется нечетной, если
- ее область определения симметрична
относительно начала координат
- выполняется равенство f(-x) = - f(x)
17.
у1
х
0
1
18.
у1
х
0
1
19.
у1
х
0
1
20.
у1
х
0
1
21.
у1
х
0
1
22.
у1
х
0
1
23.
у1
х
0
1
24.
у1
х
0
1
25.
у1
х
0
1
26. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
27. ОПРЕДЕЛЕНИЕ:
Функция f возрастает на некотороммножестве, если для любых x1 и х2 из
этого множества, таких, что x1 > х2 ,
выполнено равенство f (x1) > f(х2)
Большему значению аргумента
соответствует большее значение функции
28.
Функция f убывает на некотороммножестве, если для любых x1 и х2 из
этого множества, таких, что x1 > х2 ,
выполнено равенство f (x1) < f(х2)
Большему значению аргумента
соответствует меньшее значение функции
29.
у1
х
0
1
30.
у1
х
0
а
1
b
Возрастает ли функция на промежутке [a;b]?
31.
у1
х
0
а
1
b
Возрастает ли функция на промежутке [a;b]?
32.
у1
х
0
1
а
Возрастает ли функция на промежутке [a;b]?
b
33.
у1
х
0
а
1
b
Возрастает ли функция на промежутке [a;b]?
34. МАКСИМУМ И МИНИМУМ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
35. ОПРЕДЕЛЕНИЕ:
Точках0 называется точкой
максимума функции f, если для
всех х из некоторой
окрестности х0 выполнено
равенство
f (x) ≥ f(х0)
36.
Точках0 называется точкой
минимума функции f, если для
всех х из некоторой
окрестности х0 выполнено
равенство
f (x) ≤ f(х0)
37.
у1
х
0
1
38.
у1
х
0
1
39.
у1
х
0
1
40.
у1
х
0
1
41. НУЛИ ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
42.
у1
х
0
1
43.
у1
х
0
1
44.
у1
х
0
1
45. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА ФУНКЦИИ
Задачи с «картинками»Учебно-тренировочные материалы для подготовки к ЕГЭ
ФИПИ, «Интеллект-Центр» 2007
46.
у1
х
0
1
47.
у1
х
0
1
48.
у1
х
0
1
49.
у1
х
0
1
50.
у1
х
0
1



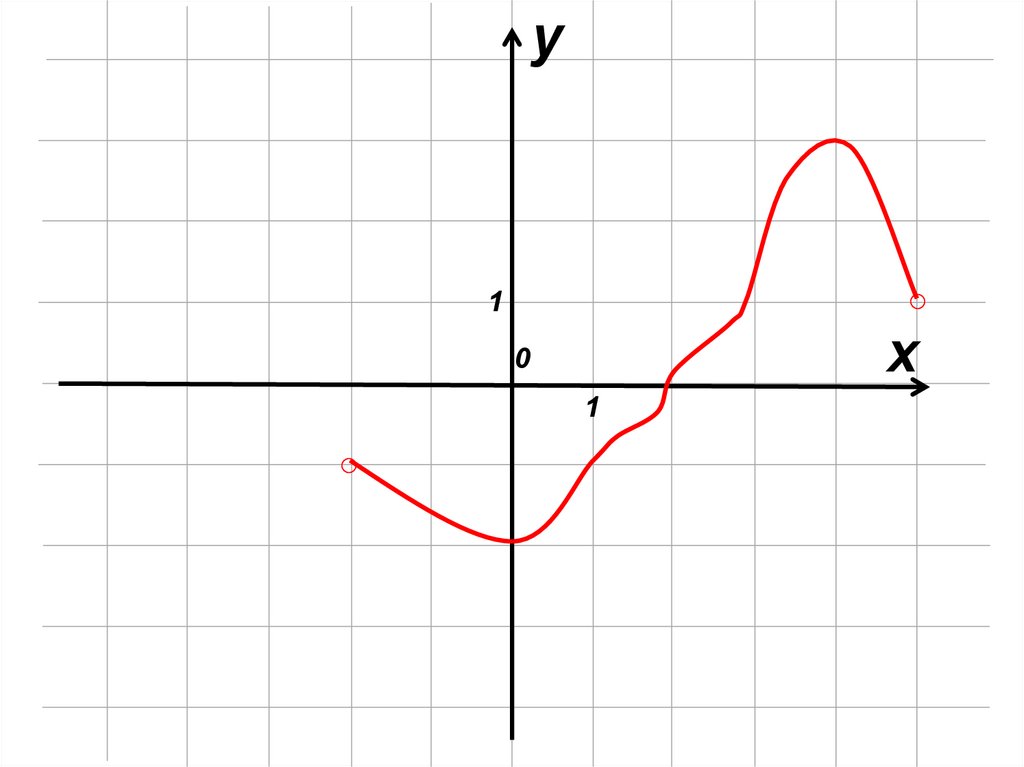


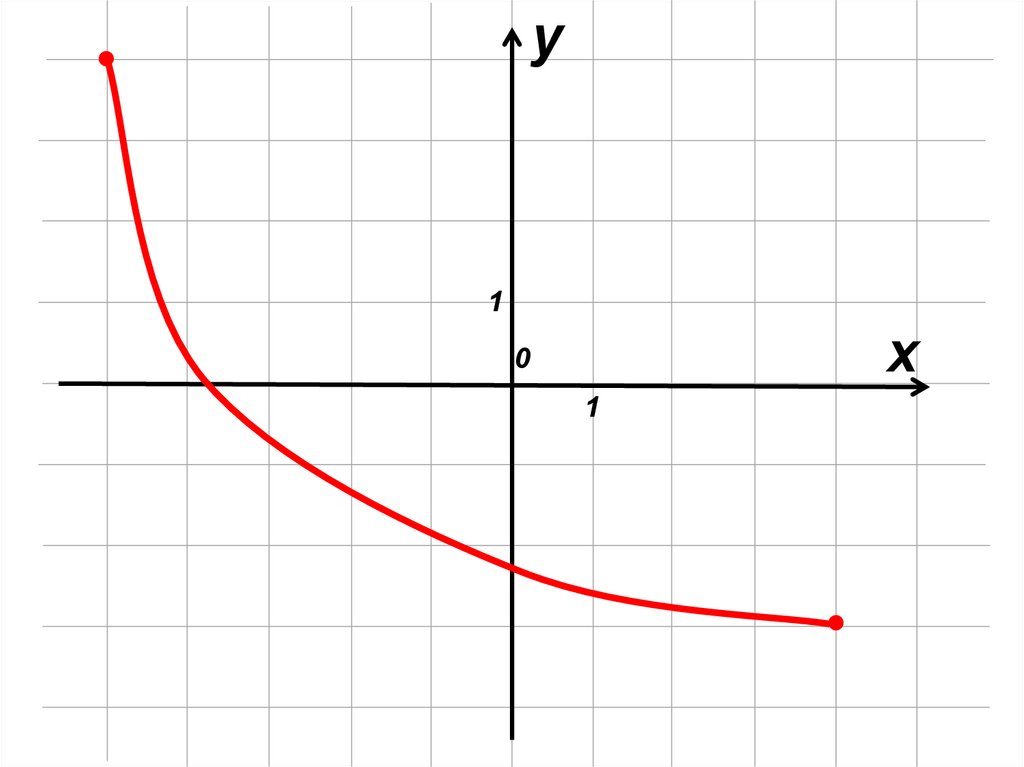




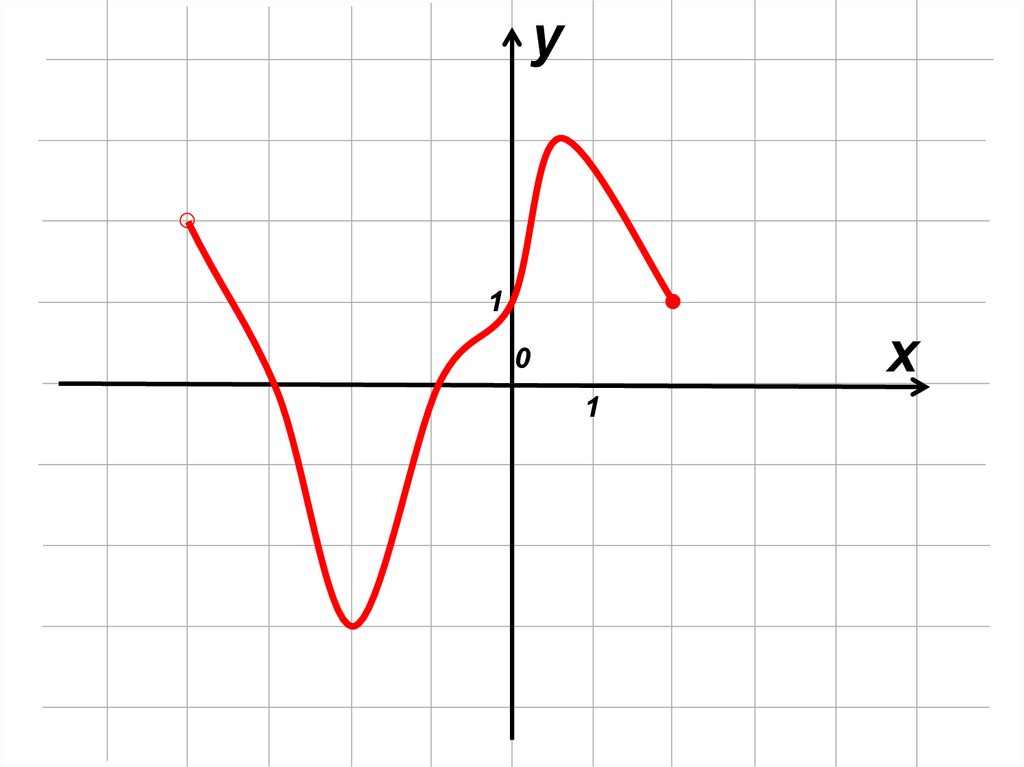








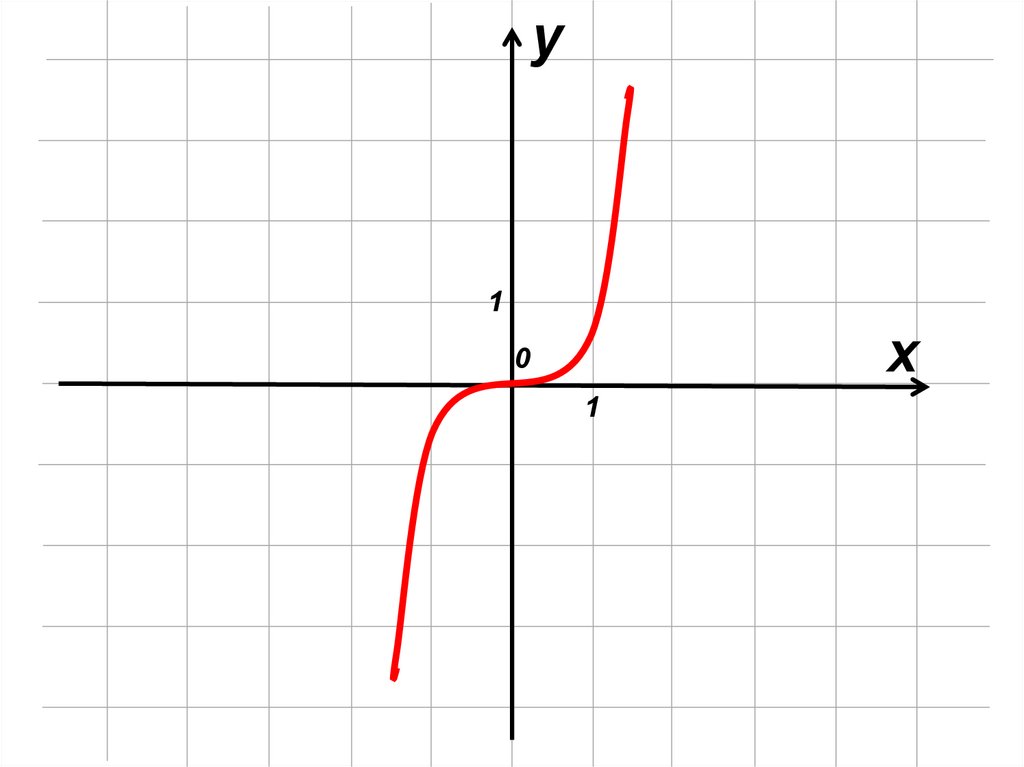























 mathematics
mathematics








