Similar presentations:
Математика. Строительство
1.
2.
4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬФУНКЦИЙ
4.1 Функция. Основные понятия и свойства
4.2 Предел функции
4.3 Непрерывность функции
3.
4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬФУНКЦИЙ
4.2 Предел функции
4.2.1. Предел функции в точке
4.2.2. Односторонние пределы
4.2.3. Конечный предел функции при бесконечно больших значениях
аргумента
4.2.4. Бесконечный предел функции в точке
4.2.5. Основные теоремы о пределах
4.2.6. Бесконечно малые функции и их свойства
4.2.7. Бесконечно большие функции и их свойства
4.2.8. Теорема о единственности предела
4.2.9. Теорема о пределе сложной функции
4.2.10. Вычисление пределов
4.2.11. Эквивалентные бесконечно малые функции
4.
4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВАФункция y = f(x) называется бесконечно малой функцией (б.м.ф.)
при x a , если
lim f ( x) 0
x a
Замечание.
Никакое, даже очень маленькое, отличное от нуля постоянное
число не может быть б.м.ф.
Свойства бесконечно малых функций.
Функция y = f(x) имеет в точке x a конечный предел А
тогда и только тогда, когда эта функция равна сумме числа А и
б.м.ф. (x) при x a :
lim f ( x) A f ( x) A ( x)
x a
5.
4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВАДалее все б.м.ф. рассматриваются при
x a.
Сумма (разность) конечного числа б.м.ф. есть снова б.м.ф.
Произведение б.м.ф. на ограниченную функцию в окрестности
точки x a есть б.м.ф.
Произведение двух б.м.ф. есть снова б.м.ф.
Произведение б.м.ф. на число есть б.м.ф.
Частное от деления б.м.ф. на функцию, имеющую отличный от
нуля предел, есть б.м.ф.
6.
4.2.7. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ И ИХ СВОЙСТВАФункция y = f(x) называется бесконечно большой функцией
(б.б.ф.) при x a , если
lim f ( x)
x a
Замечание.
Никакое, даже очень большое, постоянное число не может быть
б.б.ф.
Свойства бесконечно больших функций.
Далее все б.б.ф. рассматриваются при
x a.
Произведение двух б.б.ф. есть снова б.б.ф.
Произведение б.б.ф. на функцию, имеющую отличный от нуля
предел, есть б.б.ф.
Сумма б.б.ф. и ограниченной функции в окрестности точки
есть б.б.ф.
x a
7.
СВЯЗЬ МЕЖДУ Б.М.Ф. И Б.Б.Ф.Если f(x) - б.б.ф. при
x a , тогда
Если (x) - б.м.ф. при
x a , тогда
1
f ( x)
1
( x)
- б.м.ф. при
x a .
- б.б.ф. при
x a .
Примеры
1
0;
x x
1) lim x lim
x
1
2) lim x 0 lim .
x 0
x 0 x
НЕОПРЕДЕЛЁННОСТИ
0
0
0
1
0
0
0
8.
4.2.8. ТЕОРЕМА О ЕДИНСТВЕННОСТИ ПРЕДЕЛАЕсли предел функции y = f(x) при
единственный.
x a существует, то он
Доказательство:
Самостоятельно, от противного, используйте теорему о
связи функции, её предела и б.м.ф.
9.
4.2.9. ПРЕДЕЛ СЛОЖНОЙ ФУНКЦИИlim f ( x) b
Если
x a
и если
lim g ( y) c
y b
, причём
f ( x) b
,
(b и c – конечные),
lim g ( f ( x)) c .
тогда
x a
Замечание.
Это свойство позволяет использовать замену переменной при
вычислении пределов сложных функций.
Пример
0
1
1
2x
y
x
y
2
1
y
y
2
lim
lim
0
lim
lim 3
x
2
x
y y y 3 1 y y y y
1
x
8
3
y
8
0
x
10.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВВычисление предела:
lim f ( x) A
x x0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
Пример
3 x 1 3 1 1
lim 2
2
2
x 1
x
1
Способы раскрытия неопределённостей
11.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПравило 1.
Pn x
lim
x Q x
m
Разделить числитель и знаменатель дроби на х в наивысшей
степени.
Примеры
3x 2 1
1) lim
;
x 13 2 x x 2
3x3 x 1
2) lim 2
;
x x 4 x 3
2 x2 7
3) lim
;
x 4 2 x 4 x 2
n 3 ! 2n 1 !
4) lim
.
n 2n ! n 1 !
12.
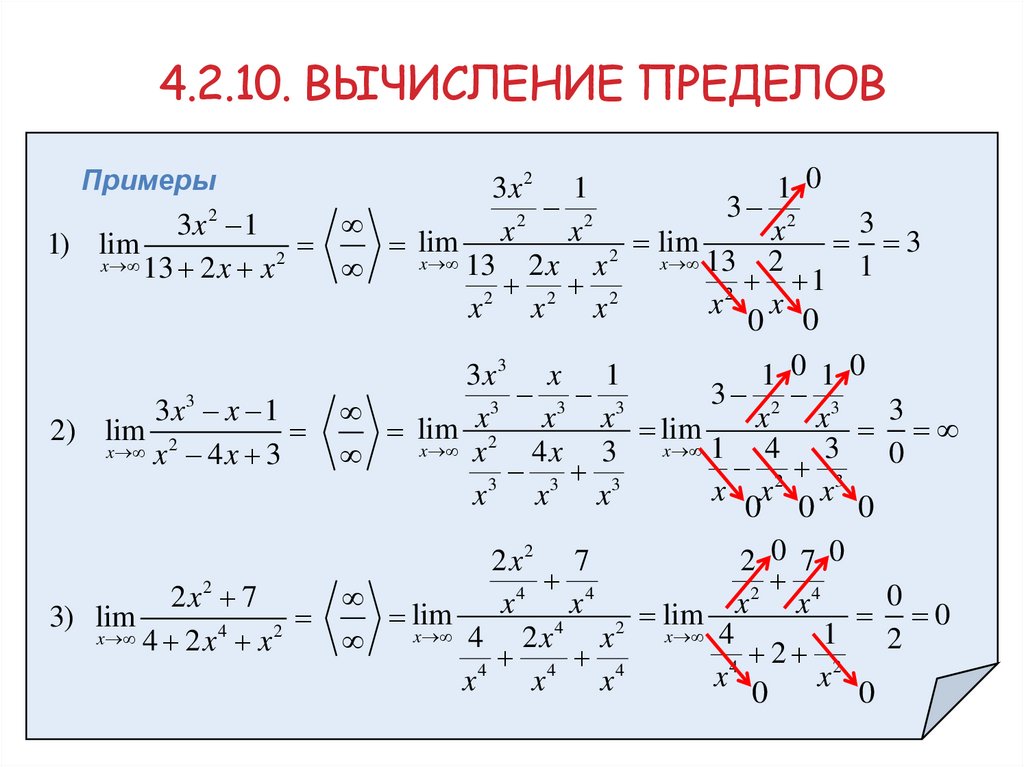
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
1 0
3x 2 1
3 2
2
2
3
3x 2 1
x
x
x
lim
lim
3
1) lim
2
x
x
13
2
x 13 2 x x 2
13 2 x x
1
1
x2 x
x2 x2 x2
0 0
3x3 x 1
2) lim 2
x x 4 x 3
3x3 x 1
1 0 1 0
3 3
3 2 3
3
3
x
x
x
x
x
lim
lim 2
x
x
1
4
3
x 4x 3
0
x x 2 x3
x3 x3 x3
0 0 0
2 0 7 0
2x2 7
4
4
2
4
0
2x2 7
x
x
x
x
lim
lim
0
3) lim
4
2
4
2
x
x
4
1
x 4 2 x x
4 2x
x
2
2
4 4
4
x4
x2
x
x
x
0
0
13.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
4)
n 3 ! 2n 1 !
n 3 ! 2n ! 2n 1
lim
lim
n 2n ! n 1 !
n 2n ! n 3 ! n 2 n 1
2n 1
2n 1
lim
lim 2
n n 2 n 1
n n 3n 2
2n 1
2 01 0
2
2
2
0
n
lim 2 n
lim n n 0
n n
n
3 2 1
3n 2
1
2
2 2
2
n 0n 0
n n n
14.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПравило 2.
Pn x
0
lim
x a Q x
0
m
1 способ: разделить числитель и знаменатель дроби на ( х - ).
2 способ: разложить числитель и знаменатель дроби на множители.
Примеры
3x 2 5 x 2
1) lim1
;
3x 1
x
3
x3 4 x 5
2) lim 3
.
2
x 1 x 2 x x 2
15.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
3x 2 5 x 2
0
1) lim1
3x 1
0
x
3
3 x 1 x 2
lim
x
1
3
3x 1
lim1 x 2
x
3
1
1
2 2
3
3
3x 2 5 x 2 0
D 52 4 3 2 49
x1
5 49 2 1
2 3
6 3
5 49 12
2
2 3
6
1
3 x 2 5 x 2 3 x x 2 3 x 1 x 2
3
x2
16.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
x3 0 x 2 4 x 5
x3 x 2
x3 4 x 5
0
2) lim 3
x 1 x 2 x 2 x 2
0
x x 5 x 1
lim
x 2x x 2
2
3
x 1
x
lim
x 1
x 5 x 1
2
x 1
x 1 x 1 x 2
x2 x
5x 5
5x 5
2
2
x 1
x2 4x 5
0
x x 5 x 1
lim
x x 2 x 2
x 1 x 2
x x 5 x 1
x x 5
1
lim
lim
2
x2 x 5
2
2
2
x 1
x 1 x 2
1 5
7
1 1 1 2 6
2
x 1
17.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПравило 3.
f x
0
lim
x a g x
0
или
lim f x g x
x
(функции f(x) и g(x) содержат корни)
Умножить числитель и знаменатель дроби на сопряжённое
выражение и использовать формулы:
2
2
a
b
a
b
a
b
;
2
2
3
3
a
b
a
ab
b
a
b
.
Примеры
x 1 1
1) lim
;
x 0
3x
2) lim
x
x3 4 x3 2 .
18.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
x 1 1
1) lim
x 0
3x
lim
x 0
x 0
3
x 1 1
1
x 1 1
3x
x 1 1
x 1 1
2
x 1 12
3x
lim
0
lim
x 0
0
x 1 1
x 1 1
lim
x 0
3
3x
1
x 1 1
0 1 1
1
6
lim
x 0
3x
x
x 1 1
19.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
2) lim
x
lim
x
lim
x
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
x3 4 x3 2
lim
x
lim x 4 x 2
3
x
6
x3 4 x3 2
3
x3 4 x3 2
6
0
20.
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛsin x
lim
1
x 0
x
Следствия:
x
lim
1
x 0 sin x
lim
x a
sin x
x
sin kx
lim
1
x 0
kx
1, где x б.м.ф. при x a
21.
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛx
1
lim 1 e
x
x
1
x
lim 1 x e
x 0
Следствия:
1
lim 1
x a
f x
lim 1 x
x a
f x
1
x
e, где f x б.б.ф. при x a
e, где x б.м.ф. при x a
22.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПравило 4.
f x
0
lim
x a g x
0
(функции f(x) и g(x) содержат
тригонометрические функции)
Применить первый замечательный предел.
Примеры
sin 3 x
1) lim
;
x 0 sin 2 x
tg x 5
2) lim 2
.
x 5 x 25
23.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
1)
0
sin 3 x
sin 3 x 3 x
sin 3 x
3x
lim
lim
lim
lim
x 0 sin 2 x
x
0
x
0
x
0
0
sin 2 x 3 x
3x
sin 2 x
3x
2 3x
2x
3
3
1 lim
lim
lim
lim 1 1,5
x 0 sin 2 x
x 0 2 sin 2 x
x 0 sin 2 x x 0 2
2
sin x 5
tg x 5
0
lim
2) lim 2
x
5
x 5 x 25
cos x 5 x 5 x 5
0
sin x 5
1
lim
lim
x 5
x
5
cos x 5 x 5
x 5
1
1
1
1
cos 5 5 5 5 cos 0 10 10
24.
4.2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ(x) и (x) называются эквивалентными бесконечно малыми
функциями при
x a , если
Обозначение:
x x при x a
( x)
lim
1
x a ( x)
Таблица основных эквивалентностей (при
1) sin x
x
2) tg x
x
3) arcsin x
4) arctg x
x2
2
5) 1 cos x
x
x
6) e 1
x
7) a 1
x
x
x ln a
x 0)
8) ln 1 x
x
9) log a 1 x
10)
1 x
k
1
x
ln a
kx
25.
4.2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИСвойства эквивалентных б.м.ф.
Если (x) ~ (x) и (x) ~ (x) при
то (x) ~ (x) при
x a,
x a.
Предел отношения двух б.м.ф. не изменится, если одну из них
(или обе сразу) заменить эквивалентными б.м.ф., т.е.
если (x) ~ (x) и (x) ~ (x) при
x a , то
( x)
( x)
lim
lim
.
x a ( x )
x a ( x )
Примеры
tg11x
1) lim 7 x ;
x 0 e
1
2) lim
x 0
ln 1 sin 4 x
arcsin x 8 x
2
.
26.
4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВПримеры
tg11x 11x 11x 0
tg11x
0
1) lim 7 x
7x
x 0 e
1
0
e 1 7 x 7 x 0
11x
11 11
lim
lim
x 0 7 x
x 0 7
7
ln 1 sin 4 x
0
2) lim
2
x 0 arcsin x 8 x
0
ln 1 sin 4 x sin 4 x 4 x 4 x 0
2
2
2
arcsin
x
8
x
x
8
x
x
8x 0
4x
4
4
lim
lim
0,5
x 0 x x 8
x 0 x 8
0 8
0
4x
lim
x 0 x 2 8 x
0


























 mathematics
mathematics Construction
Construction








