Мультимедийный курс лекций по дисциплине «Математика»

1.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Оренбургский государственный университет»
Кафедра прикладной математики
И.П. БОЛОДУРИНА, Ю.П. ИВАНОВА
Мультимедийный курс лекций
по дисциплине «Математика»
Мультимедийный курс лекций по дисциплине «Математика» (МКЛМ) предназначен для
изучения теоретических основ математики студентами направлений подготовки не
имеющих математический уклон. МКЛМ содержит 13 теоретических тем, включающих
разделы линейной алгебры, элементов аналитической геометрии, математического
анализа, теории вероятностей, а также практические демонстративные примеры по
каждой теме. Возможности МКЛМ позволяют эффективно организовать как аудиторную,
так и самостоятельную работу студентов. Достоинствами МКЛМ являются комплексность
и последовательность в изложении материала курса. Четкая структуризация учебного
материала, его наглядное и компактное представление способствуют наиболее
эффективному восприятию и усвоению его содержания.
Оренбург, 2014

2. Раздел 4 Предел и непрерывность функции действительного аргумента

Лекция 1
Пределы функции действительного аргумента
4.1.1 Функция действительного аргумента. Предел функции.
4.1.2 Бесконечно большие и бесконечно малые функции
4.1.3 Теорема о связи бесконечно малых и бесконечно больших
функций.
4.1.4 Теорема о связи между функцией, ее пределом и бесконечно
малой функцией.
4.1.5 Основные теоремы о пределах.

3. Функции действительного аргумента

Пусть X и Y – некоторые непустые множества
Если каждому элементу x множества X ставится в
соответствие один и только один элемент y множества
Y, то говорят, что на множестве X задана функция
y=f(x), то есть f : X Y
Множество X – область определения функции
Y – множество значений функции
Если элементы множеств X и Y являются
действительными числами, то функция f называется
числовой или функцией действительного аргумента

4. Функции действительного аргумента

Основными элементарными функциями являются:
степенная функция
y x , R
показательная функция
y а , a 0, a 1
x
логарифмическая функция
y log a x, a 0, a 1
тригонометрические функции
y sin x, y cos x, y tgx, y ctgx
обратные тригонометрические функции
y arcsin x, y arccos x, y arctgx, y arcctgx
Способы задания функции:
аналитический, табличный, графический, словесный

5. Предел функции в точке

Пусть функция y=f(x) определена в некоторой
окрестности точки x0 , кроме, быть может, самой
точки x0
Число А называется пределом функции в точке x0 или
при x x0 , если
( 0)( ( ) 0)( x x0 : x x0 )
будет выполнено f ( x) A
В этом случае записывают, что
lim f ( x) A .
x x0

6. Предел функции

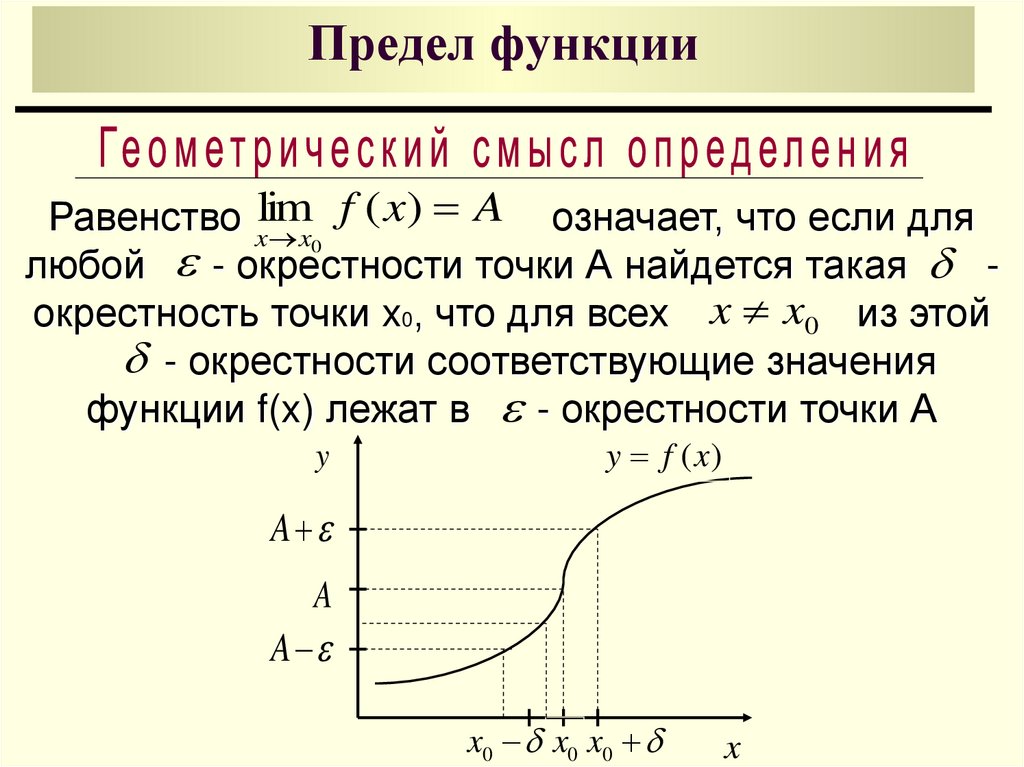
f ( x) A означает, что если для
Равенство xlim
x0
любой - окрестности точки А найдется такая окрестность точки x0, что для всех x x0 из этой
- окрестности соответствующие значения
функции f(x) лежат в - окрестности точки А
y
y f (x)
A
A
A
x0 x0 x0
x

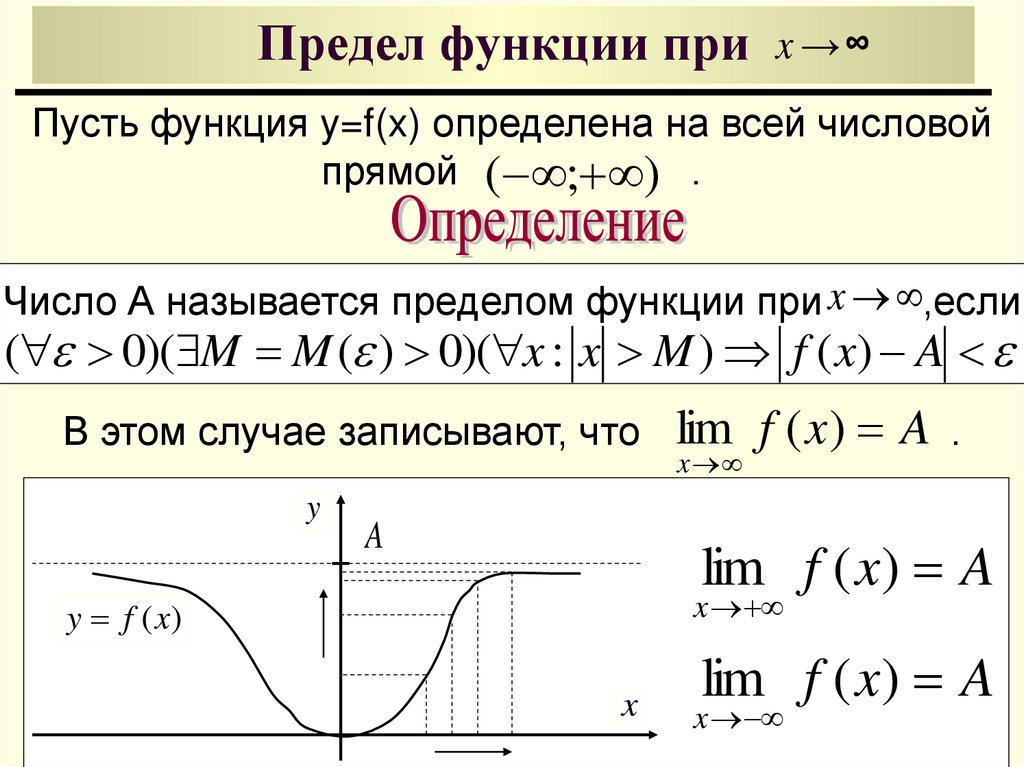
7. Предел функции при

x → ∞
Пусть функция y=f(x) определена на всей числовой
прямой ( ; ) .
Число А называется пределом функции при x ,если
( 0)( M M ( ) 0)( x : x M ) f ( x) A
В этом случае записывают, что
y
A
lim f ( x) A .
x
lim f ( x) A
x
y f (x)
x
lim f ( x) A
x

8. Бесконечно большие функции

Функция y=f(x) называется бесконечно большой
при x x0 , если
( M 0)( (M ) 0)( x : 0 x x0 ) f ( x) M
lim f ( x) .
x x0
1
lim
x 2 0 x 2
В этом случае записывают, что
y
1
y
x 2
2
x
1
lim
x 2 0 x 2
1
lim
x 2 x 2

9. Бесконечно малые функции

Функция y=f(x) называется бесконечно малой
при x x0 , если
( 0)( ( ) 0)( x : 0 x x0 ) f ( x)
В этом случае записывают, что
y
y x2
lim f ( x) 0 .
x x0
lim x 0
2
x 0 0
lim x 0
2
x 0 0
lim x 0
2
0
x
x 0

10. Свойства бесконечно малых функций

( x), ( x), ( x),.. - бесконечно малые функции
lim ( x) 0
x x0
lim ( x) 0
lim ( ( x) ( x)) 0
lim ( x) 0
lim ( ( x) ( x)) 0
x x0
x x0
x x0
x x0
(x) - ограниченная функция
lim ( x) 0
x x0
lim f ( x) A 0
x x0
lim
x x0
( x)
f ( x)
0

11. Теорема о связи б.б.ф. и б.м.ф.

Если функция (x ) является бесконечно малой при
( x) 0 ) и ( x) 0 , то функция 1 / ( x)
x x0 ( xlim
x0
1 / ( x) )
является бесконечно большой при x x0( xlim
x
0
Если функция y=f(x) является бесконечно большой
при x x0 ( lim f ( x) ), то функция 1 / f ( x )
x x0
является бесконечно малой при x x0( lim 1 / f ( x) 0 )
x x0
Докажем теорему о связи бесконечно большой
функции и бесконечно малой функции
( 1- ое утверждение)

12. Теорема о связи б.б.ф. и б.м.ф.

Пусть lim ( x) 0 , т.е. (x ) - бесконечн. малая функция.
x x0
По определению бесконечно малой функции
( 0)( ( ) 0)( x : 0 x x0 ) ( x)
Так как ( x ) 0 - ненулевая функция в окрестности
1
1
точки x0, то
( x)
Если обозначить f ( x)
1
1
, m , то последнее
( x)
неравенство запишется в виде f ( x) m ( x : 0 x x0 )
По определению следует, что lim f ( x)
x x0
f ( x) 1 / ( x) является бесконечно большой при x x0

13. Связь между функцией, ее пределом и бесконечно малой функцией

Если число А является пределом функции y=f(x) при
x x0 ( lim f ( x) А ) и (x ) - бесконечно малая функция
x x0
при x x0 ( lim ( x) 0), то функцию f(x) в окрестности
x x0
точки x0 можно представить в виде суммы числа А и
бесконечно малой функции (x ) ( f ( x) А ( x) )
Если функцию y=f(x) в окрестности точки x0 можно
представить в виде суммы числа А и бесконечно
( x) 0 ), то число А
малой функции (x ) при x x0 (xlim
x0
является пределом функции f(x) при x x0 ( lim f ( x) А )
x x0

14. Основные теоремы о пределах

Пусть f(x) и g(x) – функции, для которых существуют
пределы lim f ( x) A
lim g ( x) B
x x0
x x0
Аналогично при x
Предел суммы (разности) двух функций равен сумме
(разности) их пределов
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
Покажем, что:
lim ( f ( x) g ( x)) lim f ( x) lim g ( x) А B
x x0
x x0
x x0
(для разности доказательство аналогично)

15. Основные теоремы о пределах

По теореме о связи между функцией, ее пределом и
бесконечно малой функцией имеем
Так как lim f ( x) А , то f ( x ) А ( x ) , где
x x0
(x ) - бесконечно малая функция при x x0
Так как lim g ( x) B , то g ( x ) B ( x ) , где
x x0
(x) - бесконечно малая функция при x x0
Тогда f ( x) g ( x) А B ( x) ( x) С ( x)
По свойству бесконечно малых функций:
функция ( x) ( x) ( x) - бесконечно малая
функция при x x0
По теореме обратной для теоремы о связи между
функцией, ее пределом и бесконечно малой
( f ( x) g ( x)) А B
функцией имеем xlim
x

16. Основные теоремы о пределах

Функция может иметь только один предел при x x0
lim f ( x) А
Предположим противное: x x0
lim f ( x) B
x x0
Рассмотрим
A B lim f ( x) lim f ( x) lim ( f ( x) f ( x)) lim 0 0
x x0
Получаем
x x0
x x0
A B 0 A B
Ч.Т.Д.
x x0

17. Основные теоремы о пределах

lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
lim g ( x) 0
x x0
lim ( f ( x) / g ( x)) lim f ( x) / lim g ( x)
x x0
x x0
1. lim c f ( x) c lim f ( x)
x x0
x x0
2. lim ( f ( x)) ( lim f ( x)) , n N
x x0
n
x x0
n
x x0

18. Основные теоремы о пределах

x 14 x 32
0
( x 2)( x 16)
( ) lim
1) lim
2
x 2
x 2 ( x 2)( x 4)
x 6x 8
0
x 16 18
lim
9
x 2 x 4
2
2
3
1
2 2
2
2 x 3x 1
x x
2) lim
(
)
lim
x 4 x 2 2 x 5
x
2
5
4 2
x x
2 0 0 2 1
4 0 0 4 2