Теория пределов

1. Лекция 2 Теория пределов

2. Числовая последовательность

1
2
3
4
…
n…
2
4
8
16
…
2ⁿ…
а1
а2
а3
а4
…
аn…
an 2
n
an
1
:
n
a n 2n - 1
an ( 1) n
2
n
n 1
a n
1/2, 1/3, 1/4, ….
-аргумент
-члены последовательности

3. Предел числовой последовательности

an
1
n
a4 a3 a2
1/4 1/3 1/2
0
a1
1
1
0
n n
lim
lim a n A
n
0, N ( ) : n N an A

4. Предел функции

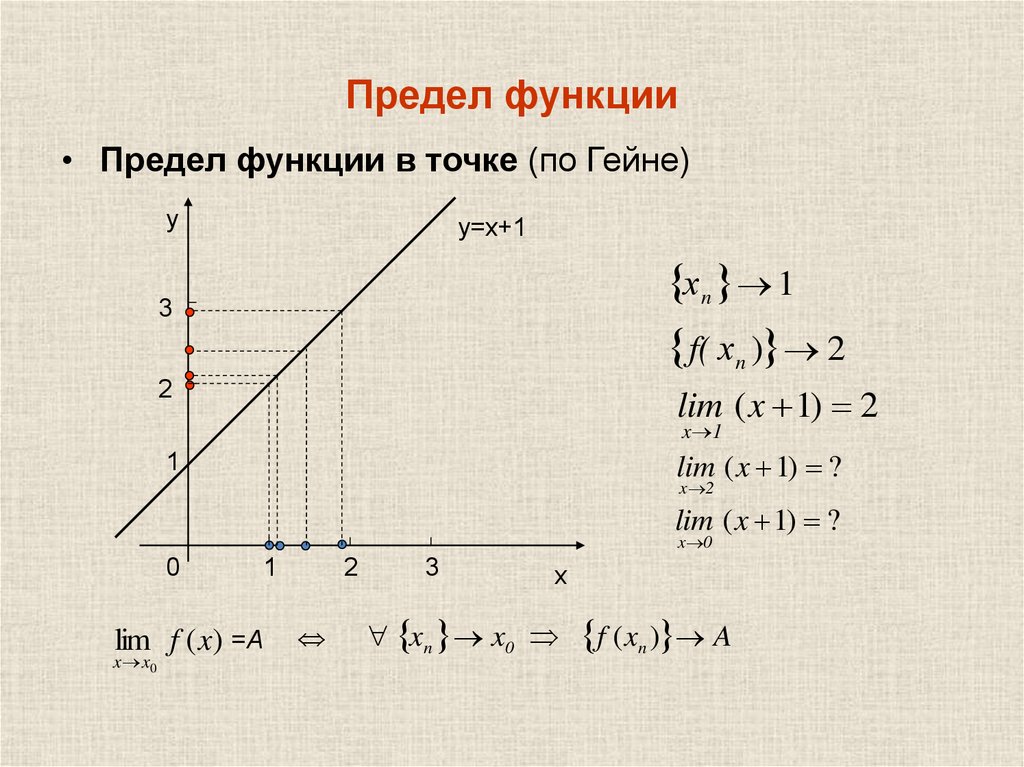
• Предел функции в точке (по Гейне)
у
у=х+1
хn 1
f( хn ) 2
3
2
lim ( x 1) 2
x 1
lim ( x 1) ?
1
x 2
lim ( x 1) ?
x 0
0
lim f ( x) =А
x x0
1
2
3
х
xn x0
f ( xn ) A

5. Предел функции в точке (по Коши)

•Предел функции в точке (по Коши)
lim f ( x) А
x x0
0 ( ) 0 : x D( f )
0, ( ) 0 : x D( f )
0 x x 0 f ( x) A
x S ( x0 ), x x0 f ( x) S ( A)
•Односторонние пределы
lim f ( x)
- справа
lim f ( x)
- слева
x x0 0
x x0 0
у
x 1, если x 0,
y
x 1, если x 0.
1
lim f ( x) 1
x 0 0
lim f ( x) 1
x 0 0
-1
х

6. Бесконечные пределы

у
А
lim f ( x) А
x
y=f(x)
х
0 ( ) 0 : x D( f )
x
1
f ( x) A
у
А
y=f(x)
lim f ( x) А
x
х
0 ( ) 0 : x D( f )
x
1
f ( x) A

7.

y
lim f ( x)
x x0
y=f(x)
x0
x
0 ( ) 0 : x D( f ) 0 x x0 f(x)
1

8. Бесконечно малые и бесконечно большие функции

(x ) - бесконечно малая при x x0 , если lim ( x) 0
x x
0
0 ( ) 0 : x D( f )
0 x x 0 ( x)
(x) - бесконечно большая при x x0, если lim ( x)
x x
0
0 ( ) 0 : x D( f )
у
0 x x 0 ( x)
lim x 2
x
y=x²
lim x 2 0
x 0
х
0
lim x 2 1
x 1
1

9. Теорема о связи между функцией и ее пределом

• Если функция при х→х0 имеет конечный предел,
равный А, то разность между функцией и значением ее
предела бесконечно мала при х→х0 :
lim f ( x) A
x x0
lim ( f ( x) A) 0
x x0

10. Теорема о связи бесконечно малой и бесконечно большой функций

(x ) - бесконечно малая при x x0
Если
( x) 0
и
в некоторой окрестности точки х0 , то
1
функция
( x)
Если
является бесконечно большой при x x0 .
(x)
- бесконечно большая при
x x0 ,
1
является бесконечно малой при
то функция
( x)
x x0 .

11. Свойства бесконечно малых функций

1. 0 0 0.
2. 0 0 0.
3. 0 C 0.
4. 0 (ограниченная функция) 0.
0
5. 0.
0
0
?
0

12. Свойства бесконечно больших функций

1. ( ) ( ) .
2. ( ) ( ) .
3. (ограниченная функция) .
4. .
5. 0 .
6.
.
?.

13. Сравнение бесконечно малых функций

Пусть α(х) и β(х) – бесконечно малые при х→х0 функции и
( x)
A.
x x0 ( x)
lim
•А≠0, А≠1:
α и β – бесконечно малые одинакового порядка
•А=0:
о( );
α – более высокого порядка малости,
•А=±∞:
β – более высокого порядка малости;
•А=1:
α и β – эквивалентные бесконечно малые, α~β

14. Свойства эквивалентных бесконечно малых

1. α ~ β ↔ β ~ α
2. α ~ β, β ~ γ ↔ α ~ γ
3. α ~ β → α = β +o(α)
(рефлексивность)
(транзитивность)
(эквивалентные
бесконечно малые отличаются друг от друга на бесконечно
малую высшего порядка).
4. Под знаком предела в отношении или
произведении бесконечно малые можно заменять
эквивалентными.

15. Основные теоремы о пределах

1.
2.
О пределе постоянной.
О единственности предела.
Необходимые условия существования конечного
предела:
3. О локальной ограниченности.
4. О локальном повторении функцией свойств
предела.
Достаточные условия существования конечного
предела:
5. Об арифметике.
6. О промежуточной функции.
7. О пределе монотонной ограниченной функции.

16.

• Теорема об арифметике
lim f ( x)
lim g ( x)
x x0
x x0
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
lim f ( x)
f ( x ) x x0
lim
x x0 g ( x )
lim g ( x)
x x0
, при условии
x x0
Пример:
lim g ( x) 0.
x x0
x 2
3
lim 2
x 1 x 5 x 1
5
f ( x) x
g ( x) x 1
lim ( f ( x) g ( x)) lim 1 1
x
x

17.

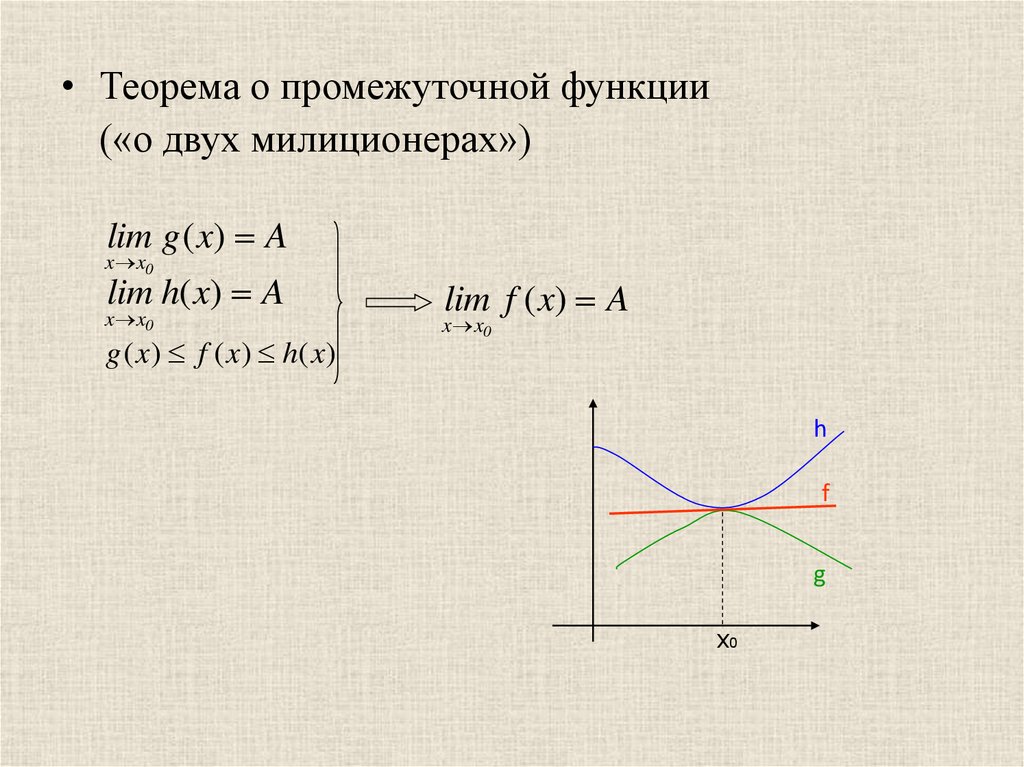
• Теорема о промежуточной функции
(«о двух милиционерах»)
lim g ( x) A
x x0
lim h( x) A
x x0
g ( x ) f ( x ) h( x )
lim f ( x) A
x x0
h
f
g
х0

18. Замечательные пределы

• Предел отношения синуса бесконечно малой дуги к самой
дуге (в радианах) равен 1:
sin x
1
x 0
x
lim
Следствия:
x
lim
1,
x 0 sin x
tg x
lim
1,
x 0 x
x
1.
x 0 tgx
lim
• Числовая последовательность
1
a n 1
n
имеет конечный предел, равный е:
n
Следствия:
x
1
lim 1 e,
x
x
1
lim 1 e
n
n
1
lim (1 ) e.
0
n

19. Вопросы к семинару 2.

Числовая последовательность и ее предел.
Предел функции в точке: определение по Гейне, по Коши.
Односторонние пределы.
Бесконечные пределы.
Бесконечно малые и бесконечно большие функции, их свойства.
Теорема о связи между функцией и ее пределом.
Теорема о связи бесконечно малой и бесконечно большой функций.
Сравнение бесконечно малых функций.
Свойства бесконечно малых функций.
Основные теоремы о пределах: о пределе постоянной, о
единственности предела, о локальной ограниченности, о локальном
повторении функцией свойств предела, об арифметике, о
промежуточной функции, о пределе монотонной ограниченной
функции.
Замечательные пределы.

20. Техника вычисления пределов

Найти пределы 1. lim
2x 4
x 2 4 x 2
x
2x
1
lim
8.
2
x 2 x 4 x 2
7. lim x 2 2 x 1
x 3 x 2
3
2
2. lim
x 2 x 2
3. lim
x
sin 2 x
x2
1
lim sin 2 x
2
x
x
2
4. lim
x 2
3x 7 x 2
.
x2 4
x 3 9 x
x 3
x 3
5. lim
6. lim
x
3x 2 4 x 5
7 x 2 8x 1
9.
sin 3x sin 7 x
4x
x 0
lim
10. lim 1
x
3
x
7x