1.51M

Category: $mathematics$ mathematics

Высшая математика в задачах: практический тренажер

1.

А.С. Гребёнкина, М.Е. Толпекина
ВЫСШАЯ МАТЕМАТИКА
В ЗАДАЧАХ:
практический тренажер
Электронное учебное пособие

А.С. Гребёнкина, М.Е. Толпекина
ВЫСШАЯ МАТЕМАТИКА
В ЗАДАЧАХ:
практический тренажер
Государственное образовательное учреждение высшего
профессионального образования «Академия гражданской защиты»
Министерства по делам гражданской обороны, чрезвычайным
ситуациям и ликвидации последствий стихийных бедствий
Донецкой Народной Республики
А.С. Гребёнкина, М.Е. Толпекина
ВЫСШАЯ МАТЕМАТИКА В ЗАДАЧАХ:
практический тренажер
Электронное учебное пособие
Электронное учебное пособие
Донецк − 2020

3.

УДК 517.1, 517.2, 378.14
Гребёнкина А.С., Толпекина М.Е. Высшая математика в задачах: практический тренажер.
– Электронное учебное пособие. – Донецк: ГОУВПО «Академия гражданской защиты»
МЧС ДНР, 2020.
Пределы функции
Рекомендовано Ученым советом ГОУВПО «Академия гражданской защиты» МЧС ДНР
как учебное пособие для обучающихся по специальности 20.05.01 «Пожарная
безопасность» очной и заочной формы обучения.
Протокол № 6 от 20.2020г.
Рецензенты:
1. В.В. Малашенко – доктор физико - математических наук, профессор, главный научный
сотрудник ГУ «Донецкий физико-технический институт им. А.А. Галкина»
Справочные материалы
2. О.М. Логачёва – кандидат физико-математических наук, доцент кафедры высшей
математики ФГБОУ ВО «Сибирский государственный университет геосистем и
технологий»
Учебное пособие содержит краткие справочные материалы и теоретические сведения
по соответствующим разделам, образцы решения типовых задач,
задания для
самостоятельной работы студентов, ответы и указания к ним. Пособие рассчитано на
студентов специальности 20.05.01 «Пожарная безопасность» очной и заочной формы
обучения.
Пособие будет полезно при изучении курса «Высшая математика» студентам любых
технических специальностей, магистрантам, аспирантам, начинающим преподавателям.
УДК 517.1, 517.2, 378.14
© Гребёнкина А.С., Толпекина М.Е., 2020
© ГОУВПО “Академия гражданской защиты” МЧС ДНР, 2020
Практический тренажер

4.

Справочные
материалы
Практический
тренажер
Актуализируем знания
Справочные
материалы
Таблица эквивалентных бесконечно малых
величин
Проверяем знания

5.

Справочные
материалы
Практический
тренажер
Актуализируем знания
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
1. Пусть функция f(x) определена в некоторой окрестности
точки х0 за исключением, быть может, самой точки.
Число А называется пределом функции в точке х0, если для
любого ε > 0 существует такое число δ(ε) > 0, что для всех х,
удовлетворяющих условию х х0 < δ выполняется неравенство
f ( x) A < ε.
2. Предел функции в точке обозначается lim f ( x) A,
х0 называется предельным значением.
х х0
3. Число А называется пределом функции f(x) при x→∞, если
для любого ε > 0 существует такое число M(ε) > 0, что для всех х,
удовлетворяющих условию х > S, выполняется неравенство
f ( x) A < ε. Обозначается: lim f ( x) A .
Проверяем знания
х
4. Число А называется пределом функции f(x) в точке х0
справа, если функция определена в некотором промежутке (х0, b]
f ( x) A
и существует предел хlim
х0
х х0
5. Число А называется пределом функции f(x) в точке х0 слева,
если функция определена в некотором промежутке [b, х0) и
существует предел lim f ( x ) A
.
х х0
х х0
Далее

6.

Справочные
материалы
Практический
тренажер
Актуализируем знания
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
6. Пределы функции в точке х0 справа и слева обозначаются
соответственно lim f ( x) и lim f ( x).
х х0 0
х х0 0
7. Функция f(x) называется бесконечно большой величиной
(б.б.в.) при х→х0, если для любого М > 0 найдется такое значение
δ(М) > 0, что для всех х, удовлетворяющих условию х х0 < δ,
выполняется неравенство f (x) > М. Если f(x) – б.б.в. при х→х0,
то lim f ( x)
x x0
8. Функция f(x) называется бесконечно малой величиной
(б.м.в.) при х→х0, если для любого ε > 0 найдется такое значение
δ(ε) > 0, что для всех x, удовлетворяющих условию х х0 < δ,
выполняется неравенство f (x) < ε. Если f(x) – б.м.в. при х→х0, то
lim f ( x) 0 .
x x
0
9. Если α(х) – б.м.в. при х→х0, то
1
– б.б.в. при х→х0.
x
sin x
1.
x 0
х x
10. Первый замечательный предел: lim
1
11. Второй замечательный предел: lim
1 e .
x
0
x
12. Выражения вида , 0 , , 1 , 0 , 0 0 , ,
называются неопределенностями. Раскрыть неопределенность
означает избавиться от нее.
Далее
0

7.

Справочные
материалы
Практический
тренажер
Актуализируем знания
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
13. Пусть α(х) и β(х) – б.м.в. при х→ х0 . Если lim
x x0
( x)
1 ,
( х)
то функции α(х) и β(х) называются эквивалентными б.м.в. при
х→х0 и обозначаются α(х) ~ β(х).
14. Функция f(x) называется непрерывной в точке х0, если
выполняются следующие условия:
– функция определена в некоторой окрестности точки х0 и самой
точке;
– существует конечный предел функции в точке х0;
– предел функции в точке х0 равен ее значению в этой точке:
lim f ( x) f ( x0 ) .
x x
0
Проверяем знания
15. Точка х0, в которой нарушается хотя бы одно из условий
непрерывности, называется точкой разрыва функции.
16. Пусть в точке х0 функция f(x) имеет разрыв.
Если оба односторонних предела функции в точке lim f ( x) и
x х0 0
lim f ( x) конечные, но неравные друг другу lim f ( x) ≠ lim f ( x) ,
x х0 0
x х0 0
x х0 0
то х0 – точка неустранимого разрыва первого рода.
Далее

8.

Справочные
материалы
Практический
тренажер
Актуализируем знания
Справочные
материалы
17. Пусть в точке х0 функция f(x) имеет разрыв.
Если оба односторонних предела функции в точке lim f ( x) и
x х0 0
lim f ( x) конечные, равные друг другу lim f ( x) = lim f ( x) ,
x х0 0
x х0 0
x х0 0
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
lim f ( x)
или lim f ( x) равен бесконечности, то х0 – точка разрыва
x х0 0
второго рода.
x х0 0

9.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Таблица эквивалентных бесконечно малых
величин
При х→0 следующие функции эквивалентны:
sin x x
arcsin x x
tg x x
arctg x x
1 – cos x
х2
2
ex – 1 x
Проверяем знания
ax – 1 x ln a
ln (1 + x) x
n
1 х
x
n

10.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
2. Указать, чему равен предел lim 1 1
x
x
3. Указать, чему равен предел lim f1 x f 2 x ,
1. Указать, чему равен предел lim
x 0
x x0
если lim f1 ( x) A , lim f 2 ( x) B .
x x
x x
?
?
0
0
4. Указать, чему равен предел lim ( x) ,
x x
если α(x) – б.м.в. при x→x0.
5. Указать, чему равен предел lim 1 , если
x x
( x)
β(x) – б.б.в. при x→x0.
0
0
Проверяем знания
?
?
?
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
условие: lim f ( x) , lim f ( x) – конечные,
x x 0
x x 0
?
0
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
Далее

11.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Применение производной
Задание
Ответ
8. Указать, какое условие выполняется, если
α(х), β(х) – б.м.в. при х→х0 и α(х) ~ β(х).
?
9. Указать вид неопределенности в пределе
f ( x)
lim
, если lim f ( x) 0, lim g ( x) 0.
x x0 g ( x)
x x0
x x0
?
10. Указать, разрыв какого рода терпит
функция f(x) в точке х0, если lim f ( x) .
?
x x0 0

12.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
?
?
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
1
0
?
?
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
?
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0

13.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
е
?
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
?
0
?
?
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
?
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0

14.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
?
А+В
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
?
0
?
?
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
?
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0

15.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
?
?
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
?
0
0
?
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
?
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0

16.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
?
?
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
?
0
?
0
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
?
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
?
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0

17.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
?
1. Указать, чему равен предел lim
x 0
?
?
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
?
0
?
0
Проверяем знания
0
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
lim f ( x) lim f ( x) f x0
x x 0
x x 0
0
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) – конечные,
f ( x), xlim
условие: xlim
x 0
x 0
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
0
0
?

18.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Задание
Ответ
sin x
x
x
1
2. Указать, чему равен предел lim 1
x
x
f1 x f 2 x ,
3. Указать, чему равен предел lim
x x
1. Указать, чему равен предел lim
x 0
0
f 2 ( x) B .
f1 ( x) A , lim
если lim
x x
x x
?
?
0
0
( x) ,
4. Указать, чему равен предел lim
x x
если α(x) – б.м.в. при x→x0.
1
5. Указать, чему равен предел lim
, если
x x
(
x
)
β(x) – б.б.в. при x→x .
0
0
Проверяем знания
?
0
6. Указать, какое условие выполняется, если в
точке х0 функция f(x) непрерывная.
7. Указать, какого вида разрыв терпит функция
f(x) в точке х0, если в этой точке выполняется
f ( x) , lim f ( x) – конечные,
условие: xlim
x 0
x x 0
0
?
?
?
Разрыв
1-го рода
0
lim f ( x) lim f ( x)
x x0 0
x x0 0
Далее

19.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Проверяем знания
Задание
Ответ
8. Указать, какое условие выполняется, если
α(х), β(х) – б.м.в. при х→х0 и α(х) ~ β(х).
lim
x x
0
( x)
1
( x)
9. Указать вид неопределенности в пределе
f ( x)
lim
, если lim f ( x) 0, lim g ( x) 0.
x x0 g ( x)
x x0
x x0
?
10. Указать, разрыв какого рода терпит
функция f(x) в точке х0, если lim f ( x) .
?
x x0 0

20.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Проверяем знания
Задание
Ответ
8. Указать, какое условие выполняется, если
α(х), β(х) – б.м.в. при х→х0 и α(х) ~ β(х).
9. Указать вид неопределенности в пределе
f ( x)
lim
, если lim f ( x) 0, lim g ( x) 0.
x x0 g ( x)
x x0
x x0
10. Указать, разрыв какого рода терпит
функция f(x) в точке х0, если lim f ( x) .
x x0 0
?
0
0
?

21.

Справочные
материалы
Практический
тренажер
Справочные
материалы
Актуализируем знания
Таблица эквивалентных бесконечно малых
величин
Проверяем знания
Проверяем знания
Задание
Ответ
8. Указать, какое условие выполняется, если
α(х), β(х) – б.м.в. при х→х0 и α(х) ~ β(х).
?
9. Указать вид неопределенности в пределе
f ( x)
lim
, если lim f ( x) 0, lim g ( x) 0.
x x0 g ( x)
x x0
x x0
?
10. Указать, разрыв какого рода терпит
функция f(x) в точке х0, если lim f ( x) .
x x0 0
Разрыв
2-го рода

22.

Справочные
материалы
Практический
тренажер
Учимся решать
Практический
тренажер
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции

23.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Учимся решать
Пределы функций
Пределы функции
Найти пределы.
x( x 4) 5 (5 4) 45
1. lim
x 5
Ответ: 45.
x
1
1
2. lim
x 1
x 1 1 1 0
Ответ: ∞.
2
3x 2 4 x 7 3 1 4 1 7 0 0
3. lim
x 1
2 x 2 3 x 5 2 12 3 1 5 0 0
Непрерывность
функции
3x 2 4 x 7 0,
Решаем самостоятельно
Пределы функций
Непрерывность
функции
D 4 2 4 3 ( 7) 100,
4 10
7
x1
,
2 3
3
4 10
x2
1.
2 3
7
3x 2 4 x 7 3 x x 1 3x 7 x 1
3
Далее

24.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
Пределы функции
2 x 2 3x 5 0
D 32 4 2 ( 5) 49
3 7
5
x1
,
2 2
2
3 7
x2
1.
2 2
5
2 x 2 3x 5 2 x x 1 2 x 5 x 1
2
3x 7 x 1 lim 3x 7 3 1 7 10
lim
x 1
2 x 5 x 1 x 1 2 x 5 2 1 5 7
10
Ответ: .
7
4.
lim
x 0
x2 4 2
( x 2 4 2)( x 2 4 2)( x 2 9 3)
0
lim
x 2 9 3 0 x 0 ( x 2 9 3)( x 2 9 3)( x 2 4 2)
x
lim
x
x 0
lim
x 0
2
2
9 9 (
4 4 ( x 2 9 3)
x2 9 3
x2 4 2
2
Ответ: .
3
x 2 4 2)
lim
x 0
x 2 ( x 2 9 3)
x 2 ( x 2 4 2)
2 2 2
3 3 3
Далее

25.

Справочные
материалы
Практический
тренажер
Пределы функции
Найти пределы.
Практический
тренажер
x 2 3x 2 0,
5.
Учимся решать
Пределы функций
Непрерывность
функции
xlim
0
Пределы функций
( x 2)( x 1)( x 6 2)
( x 2)( x 1)( x 6 2)
lim
x 6 4
( x 6 2)( x 6 2) x 0
lim
( x 1)( x 6 2) 4
x 0
Решаем самостоятельно
Непрерывность
функции
D 32 4 1 2 1,
x 2 3x 2 0
3 1
lim
x
2,
1
x 2
2
x 6 2 0
3 1
x2
1,
2
x 2 3x 2 x 2 x 1
Ответ: –4.
sin 5 x
5x
2 sin 5 x 0
2 1 5 x 10
5
x
lim
lim
lim
x 0
x 0
sin 3x 0 x 0 sin 3x 3x
1 3x
3
3x
2
6.
Ответ:
10
.
3
Далее

26.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Пределы функции
Найти пределы.
2 sin
7.
cos9 x cos13 x 0
lim
tgx 2
0 x 0
sin 2 x ~ 2 x
2 lim
x 0
Учимся решать
Пределы функций
lim
x 0
sin 2 x sin 22 x sin 22 x ~ 22 x
2 x 22 x
2 lim
88
2
2
2
x 0
tgx
x2
tgx ~ x
x 0
Ответ: 88.
Непрерывность
функции
9x3
9 x 2 x 10
Пределы функций
Непрерывность
функции
8.
2x
10
x
x
x3
lim
x 3 x 2 15 x 17
x 3 x 2 15 x 17
3 3
x3
x
x
2 10
9 2 3
x
x 9 0 0
lim
15 17
x 3
2 3 0 0 0
x x
x
3
Решаем самостоятельно
9 x 13 x
9 x 13 x
sin
2
2
2
tgx
lim
3
3
Ответ: ∞.
Далее

27.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Пределы функции
Найти пределы.
3x 2
9.
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
3x 14 x 19
10.
14 x
19
x
x
x2
lim
x 5 x 2 16 x 8
x 5 x 2 16 x 8
2 2
x2
x
x
14 19
3 2
3 0 0 3
x x
lim
16 8 5 0 0 5
x
5 2
x x
Ответ: 3 .
5
2
lim
2
x 19 x
lim
x 19 x x
x 19 x x 19 x
x 19 x
19
19
19
0
x 19 x
lim x 19 x xlim
x
xlim
2
Ответ: 0.
Далее

28.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Пределы функции
Найти пределы.
11.
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
x 2
6
1
x
lim
3
x
1
x
Учимся решать
Пределы функций
x 6
lim
x x 3
Ответ:
12.
x 2
6
1
x
lim
3
x
1
x
x 2
1
x
x
6
6
6 6
6
lim 1
lim 1
6
1
x x x 12 x x e e3
lim
x
3
3
x
3
e3
3
x
3
1
lim 1
lim 1
x
x
x
x
x
x
2
e 3.
lim 1 5 sin 2 x
x 0
6
x 1
x
lim
x
3
x 1
x
lim e 5 cos
2
x
x 0
Ответ:
2
ctg x
e 5 cos
1 lim 1 5 sin 2 x
x 0
2
0
1
5 sin 2 x
5 cos 2 x
e5
e5 .
Далее

29.

Справочные
материалы
Практический
тренажер
Непрерывность функции
Практический
тренажер
1.
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Исследовать функцию на непрерывность, построить схематический
график.
1
x 3 , x 3
y 2 x , 3 x 0
x 2 4,0 x 2
x 2, x 2
Решение.
Функция неэлементарная. Точки подозрительные на разрыв:
х = –3, х = 0, х = 2.
Найдем односторонние пределы функции в каждой из этих точек.
1
1
1
lim y lim
;
x -3-0
x 3 0 x 3 3 0 3
0
lim y lim 2 x 2 3 0 5.
x -3 0
Пределы функций
Непрерывность
функции
x 3 0
Т.к. lim y , то в точке х = –3 функция терпит разрыв 2-го рода.
x -3-0
lim y lim 2 x 2 0 2;
x 0-0
x 0 0
lim y lim x2 4 02 4 4.
x 0 0
x 0 0
Т.к. lim y lim y и оба предела конечные, то в точке х = 0 функция
x 0-0
x 0 0
терпит разрыв 1-го рода.
lim y lim x 2 4 22 4 0;
Далее
x 2-0
x 2 0

30.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Непрерывность функции
lim y lim x 2 22 2 2.
x 2 0
x 2 0
Т.к. lim y lim y y 2 , то в точке х = 2 функция непрерывная.
x 0-0
x 0 0
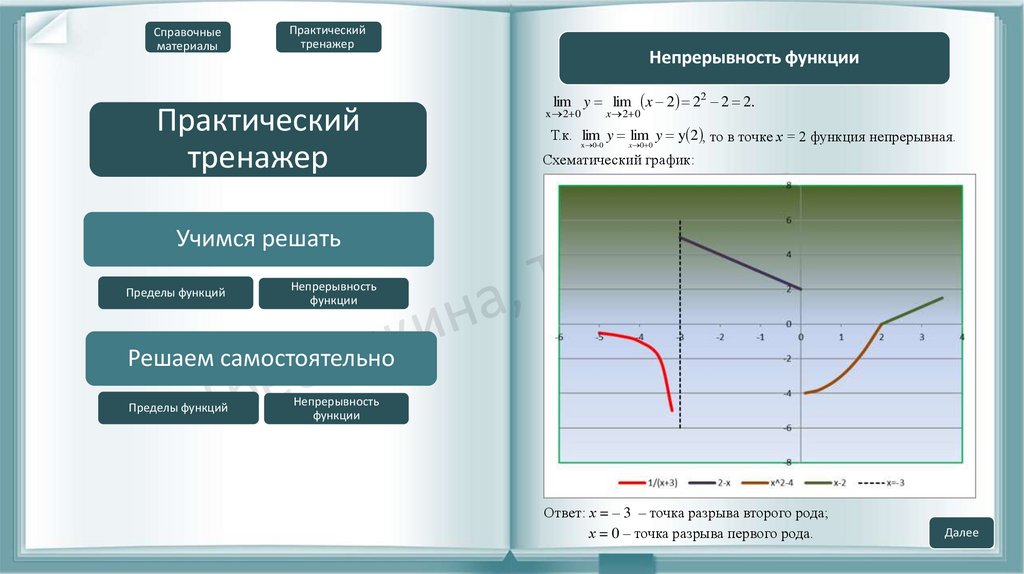
Схематический график:
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
Ответ: х = – 3 – точка разрыва второго рода;
х = 0 – точка разрыва первого рода.
Далее

31.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Непрерывность функции
Исследовать функцию на непрерывность, построить схематический
график.
2.
x2 1
y
x 5
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
x 2 1 5 0 2 1 26
lim y lim
;
x 5- 0
x 5 0 x 5
3 0 5
0
x 2 1 5 0 2 1 26
lim y lim
.
x 5 0
x 5 0 x 5
5 0 5
0
Т.к. односторонние пределы бесконечные, то в точке х = 5 функция
терпит разрыв 2-го рода.
Далее

32.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Непрерывность функции
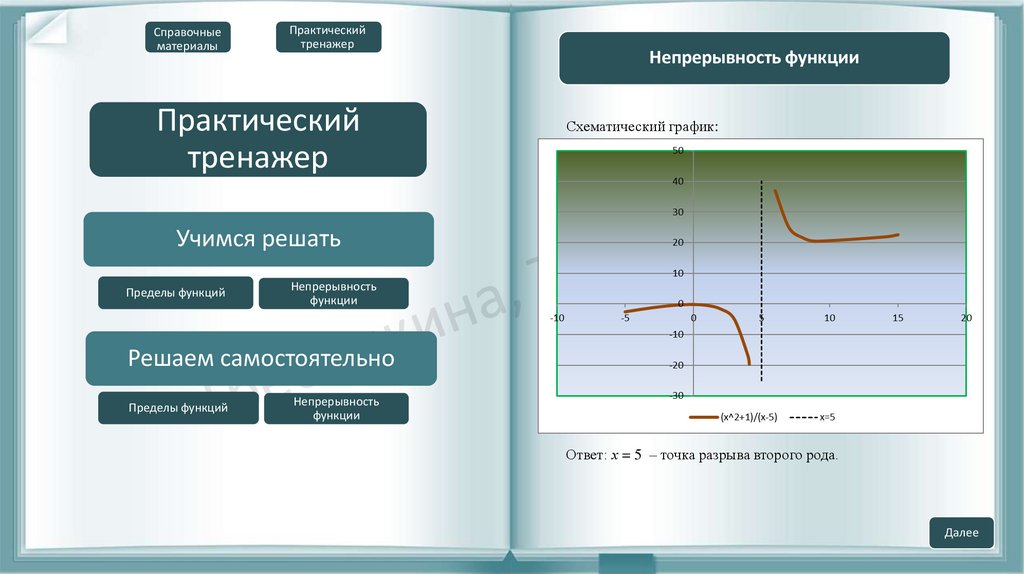
Схематический график:
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
Ответ: х = 5 – точка разрыва второго рода.
Далее

33.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Учимся решать
Пределы функции
Найти пределы
1.
2.
3.
4.
Пределы функций
Непрерывность
функции
Решаем самостоятельно
5.
6.
7.
Пределы функций
Непрерывность
функции
Ответ
x 2 x 12
x 2 11x 28
5 x2 2
lim
x 1
2x 1 1
x 11 2
lim
x 7
x 7
2 sin 3 x 2
lim
x 0
sin 2 6 x
xtgx
lim
x 0
1 cos5 x
5 x 4 3x 2 2
lim 5
x
4x 2x2 x
9x3 7x
lim
x
19 x 3 12 x 2 3
lim
x 4
8. lim
x
x 2 14 x
9. lim 5 x 1
x
5x 7
5
10. lim 2 cos x sin 0, 5 x
?
?
?
?
?
?
?
?
3x
2
x 0
?
?

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Непрерывность функции
Исследовать функцию на непрерывность, построить
схематический график.
1.
Учимся решать
Пределы функций
?
Ответ:
Непрерывность
функции
Решаем самостоятельно
Пределы функций
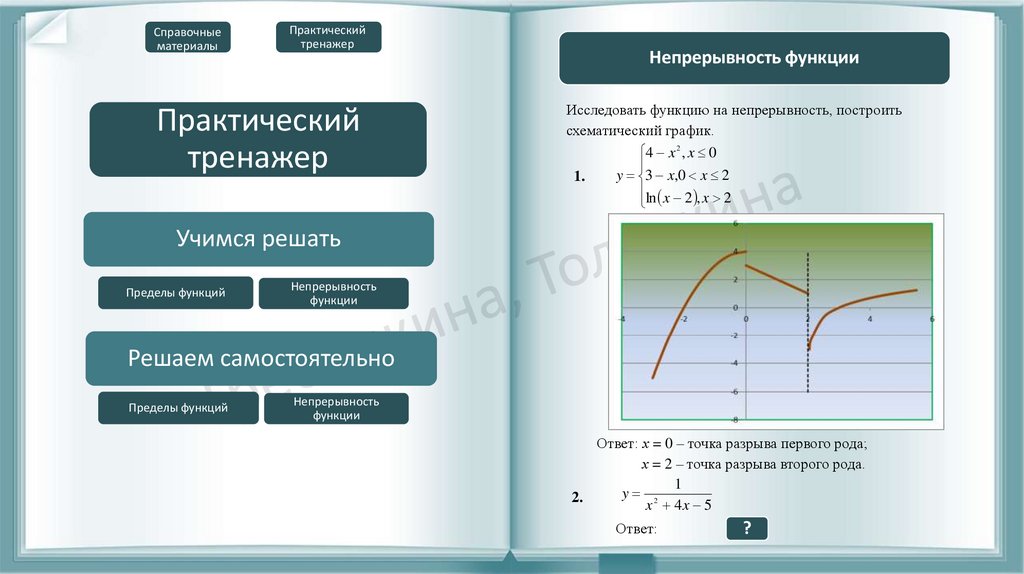
4 x 2 , x 0
y 3 x,0 x 2
ln x 2 , x 2
Непрерывность
функции
2.
y
Ответ:
1
x 4x 5
2
?

45.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Непрерывность функции
Исследовать функцию на непрерывность, построить
схематический график.
4 x 2 , x 0
y 3 x,0 x 2
1.
ln x 2 , x 2
Учимся решать
Пределы функций
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
Ответ: х = 0 – точка разрыва первого рода;
х = 2 – точка разрыва второго рода.
1
y 2
2.
x 4x 5
Ответ:
?

46.

Справочные
материалы
Практический
тренажер
Практический
тренажер
Учимся решать
Непрерывность функции
Исследовать функцию на непрерывность, построить
схематический график.
4 x 2 , x 0
y 3 x,0 x 2
1.
ln x 2 , x 2
Ответ:
?
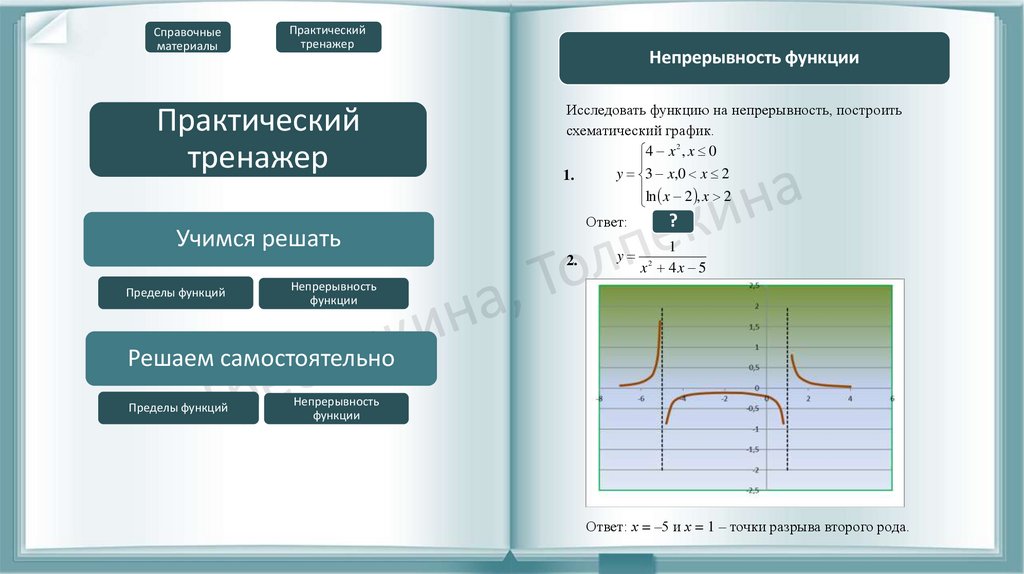
2.
Пределы функций
y
1
x 4x 5
2
Непрерывность
функции
Решаем самостоятельно
Пределы функций
Непрерывность
функции
Ответ: х = –5 и х = 1 – точки разрыва второго рода.

English Русский Rules