Определенный интеграл (для высшей математики)

1. Тема:

Определенный интеграл,
его основные свойства.
Формула НьютонаЛейбница. Приложения
определенного
интеграла.
Скопировано с сайта http://www.myshared.ru/slide/301777/

2. ПЛАН

1.
2.
3.
4.
5.
Понятие определенного интеграла.
Свойства определенного интеграла.
Метод замены переменной.
Несобственные интегралы.
Приложения определенного
интеграла.

3. 1. Понятие определенного интеграла

К понятию определенного интеграла
приводит задача нахождения площади
криволинейной трапеции.
Пусть на некотором интервале [a,b] задана
непрерывная функция y f ( x) 0
Задача:
Построить ее график и найти F площадь
фигуры, ограниченной этой кривой, двумя
прямыми x = a и x = b, а снизу – отрезком оси
абсцисс между точками x = a и x = b.

4.

Фигура aABb называется
криволинейной трапецией

5. Def.

b
Под определенным интегралом
f ( x)dx
a
от данной непрерывной функции f(x) на
данном отрезке [a;b] понимается
соответствующее приращение ее
первообразной, то есть
F (b) F ( a ) F ( x) /
b
a
Числа a и b – пределы интегрирования,
[a;b] – промежуток интегрирования.

6. Правило:

Определенный интеграл равен разности
значений первообразной
подынтегральной функции для верхнего
и нижнего пределов интегрирования.
Введя обозначения для разности
b
F (b) F (a) F ( x) / a
b
f ( x)dx F (b) F (a)
a
Формула Ньютона – Лейбница.

7. Готфрид Вильгельм Лейбниц

(1646 – 1716 гг.)
Выдающийся немецкий
мыслитель Готфрид
Вильгельм
Лейбниц принадлежал к роду,
известному своими учеными и
политическими деятелями. Он
изобретал всевозможные универсальные
приемы для решения всех задач сразу и,
может быть, поэтому вслед за Паскалем стал
строить вычислительные устройства.

8. Исаак НЬЮТОН (Newton)

(04.01.1643 - 31.03.1727)
Английский физик и математик,
создатель теоретических основ
механики и астрономии. Он
открыл закон всемирного
тяготения, разработал (наряду с
Г. Лейбницем)
дифференциальное и
интегральное исчисления,
изобрел зеркальный телескоп и был автором
важнейших экспериментальных работ по оптике.
Ньютона по праву считают создателем
"классической физики".

9. 2. Основные свойства определенного интеграла.

1)Величина определенного интеграла не
зависит от обозначения переменной
интегрирования, т.е.
b
b
a
a
f ( x)dx f (t )dt
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми
пределами
интегрирования равен нулю
a
f ( x)dx F (a) F (a) 0
a

10.

3) При перестановке пределов интегрирования
определенный интеграл меняет свой знак на
обратный
b
a
a
b
f ( x)dx F (b) F (a) F (a) F (b) f ( x)dx
(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число
частичных промежутков, то определенный интеграл,
взятый по промежутку [a;b], равен сумме
определенных интегралов, взятых по всем его
частичным промежуткам.
b
c
a
a
b
f ( x)dx f ( x)dx f ( x)dx
c

11.

5)Постоянный множитель можно
выносить за знак определенного
интеграла.
6)Определенный интеграл от
алгебраической суммы конечного числа
непрерывных функций равен такой же
алгебраической сумме определенных
интегралов от этих функций.

12. 3. Замена переменной в определенном интеграле.

3. Замена переменной в
определенном интеграле.
b
f ( x)dx f (t ) (t )dt
a
где a ( ), b ( ), (t ) [a; b]
для t [ ; ] , функции (t ) и (t )непрерывны
на ; .
5
Пример: x 1dx = x 1 5
1
x 1 t
t 0 4
dt dx 4
2 32 4 2
2
16
1
4
t
dt
t
t
t
4
2
0
5
=
0
0
0
3
3
3
3
3

13. Потренируемся!

14. 4. Несобственные интегралы.

4. Несобственные интегралы.
Def: Пусть функция f(x) определена на
бесконечном интервале [a; + ) и
интегрируется на любом интервале [a;b],
где b < + . Еслиbсуществует
lim
f ( x)dx,
b
a
то этот предел называется несобственным
интегралом функции f(x) на интервале
[a; + ) и обозначается
f ( x)dx.
a

15.

Таким образом, по определению,
b
f ( x)dx lim f ( x)dx lim ( F (b) F (a))
a
b
a
b
Если этот
предел некоторое
число, то
интеграл f ( x)dx
a
называется
сходящимся, если предела не существует, или он
равен , то говорят, что интеграл расходится.

16. ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis)

(1781–1840 гг.)
Французский математик,
механик и физик. В 1811 он
вывел получившее
широкое применение
уравнение, связывающее
электрический потенциал с
плотностью
пространственного распределения
заряда (уравнение Пуассона).

17. Интеграл Пуассона:

e
x2
a2
dx
если а = 1, то
e
x2
dx
Интеграл сходится, и его значение
.

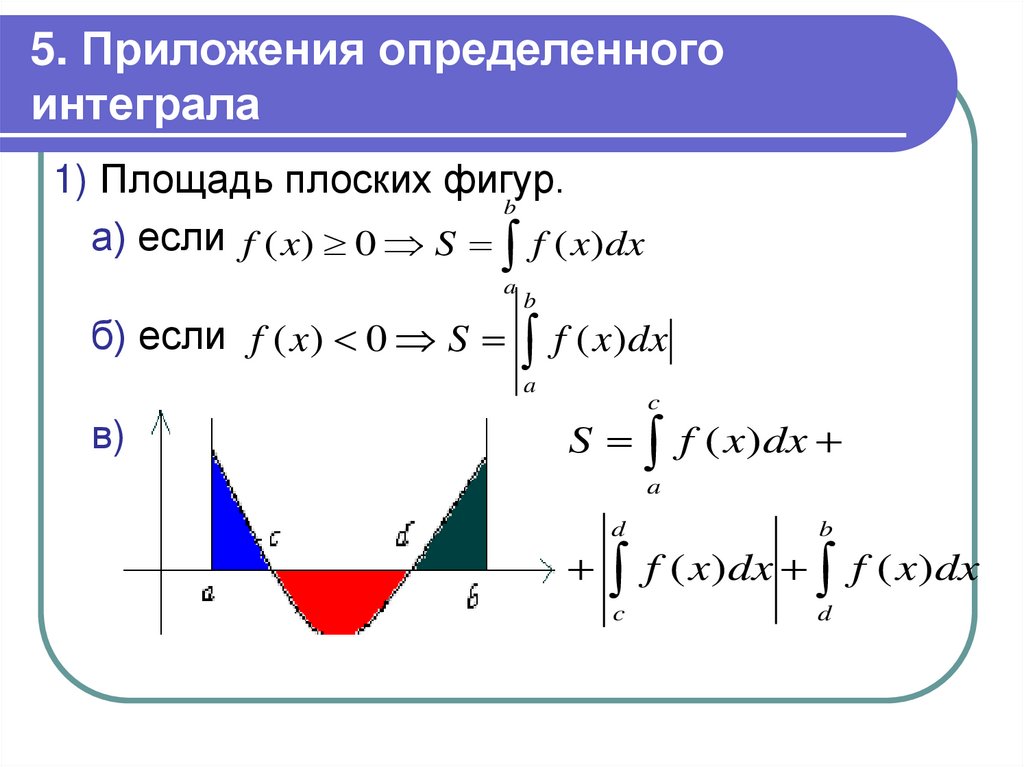
18. 5. Приложения определенного интеграла

1) Площадь плоских фигур.
b
а) если f ( x) 0 S f ( x)dx
a
b
б) если f ( x) 0 S f ( x) dx
a
в)
c
S f ( x)dx
a
d
b
c
d
f ( x)dx f ( x)dx

19.

b
г) S f ( x) ( x) dx
a
b
2) A F ( x)dx интеграл от
a
величины силы по длине пути.

20. 3) Прирост численности популяции.

N(t) прирост численности за
промежуток времени от t0 до T, v(t) –
скорость роста некоторой популяции.
T
N (t ) v (t ) dt интеграл от скорости
t0
по интервалу времени ее
размножения.