Similar presentations:
Многогранники. Призма и её основные элементы. Построение сечений
1. Содержание
1.2.
3.
4.
5.
6.
Многогранники
Призма и её основные элементы
Построение сечений
Виды призм
Развертка и поверхность призмы
Параллелепипед
2. Многогранники.
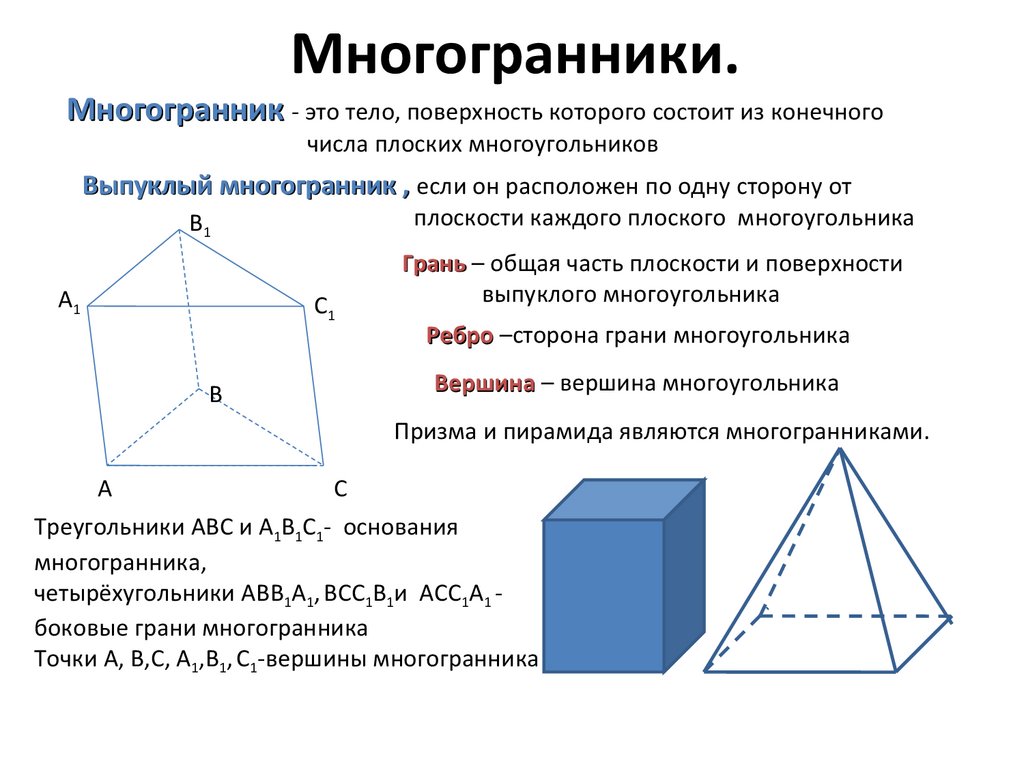
Многогранник - это тело, поверхность которого состоит из конечногочисла плоских многоугольников
Выпуклый многогранник , если он расположен по одну сторону от
плоскости каждого плоского многоугольника
B1
А1
C1
Грань – общая часть плоскости и поверхности
выпуклого многоугольника
Ребро –сторона грани многоугольника
B
Вершина – вершина многоугольника
Призма и пирамида являются многогранниками.
А
C
Треугольники ABC и A1B1C1- основания
многогранника,
четырёхугольники ABB1A1, BСC1B1и АСC1A1 боковые грани многогранника
Точки А, В,С, A1,B1, C1-вершины многогранника
3. ПРИЗМА И ЕЕ ОСНОВНЫЕ ЭЛЕМЕНТЫ.
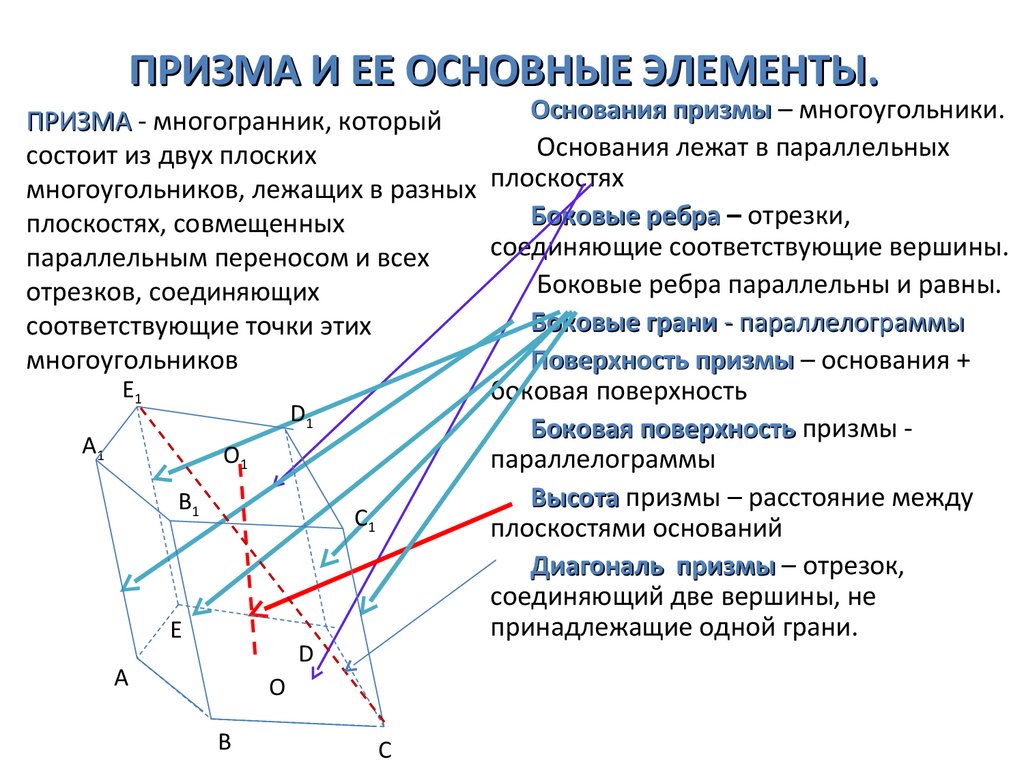
Основания призмы – многоугольники.ПРИЗМА - многогранник, который
Основания лежат в параллельных
состоит из двух плоских
многоугольников, лежащих в разных плоскостях
Боковые ребра – отрезки,
плоскостях, совмещенных
соединяющие соответствующие вершины.
параллельным переносом и всех
Боковые ребра параллельны и равны.
отрезков, соединяющих
Боковые грани - параллелограммы
соответствующие точки этих
Поверхность призмы – основания +
многоугольников
E1
боковая поверхность
D1
Боковая поверхность призмы A1
О1
параллелограммы
Высота призмы – расстояние между
B1
C1
плоскостями оснований
Диагональ призмы – отрезок,
соединяющий две вершины, не
принадлежащие одной грани.
E
D
A
О
B
C
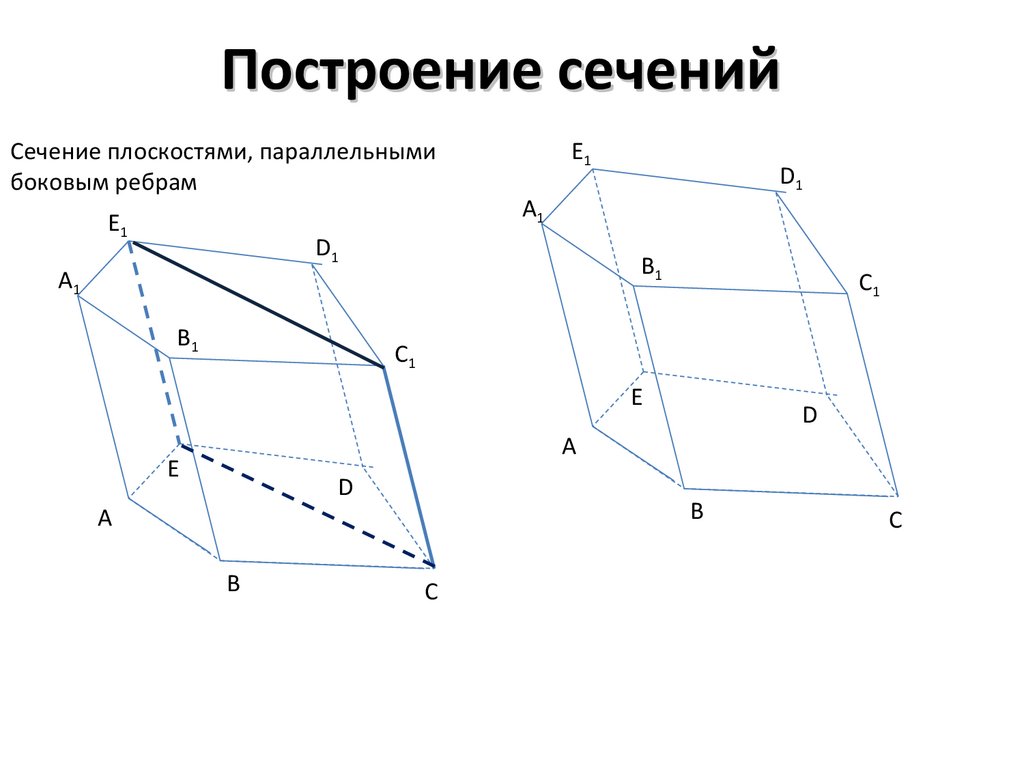
4. Построение сечений
Сечение плоскостями, параллельнымибоковым ребрам
E1
D1
A1
E1
D1
B1
A1
B1
C1
C1
E
D
A
E
D
B
A
B
C
C
5.
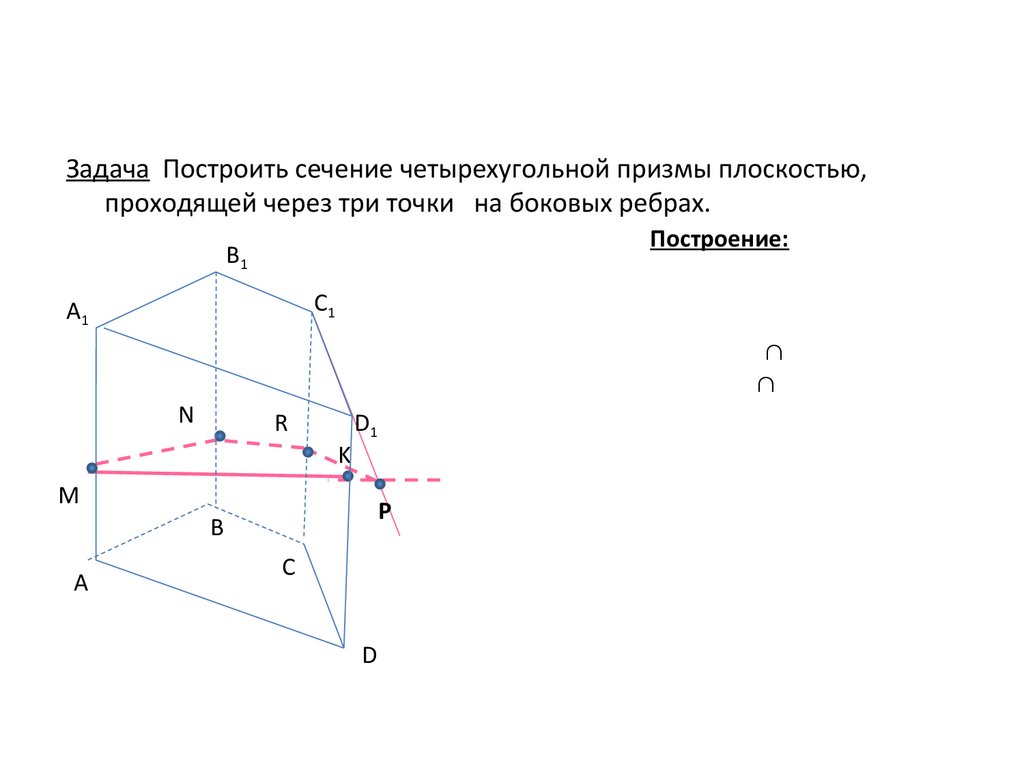
Задача Построить сечение четырехугольной призмы плоскостью,проходящей через три точки на боковых ребрах.
Построение:
B1
C1
А1
N
R
D1
K
M
P
В
А
С
D
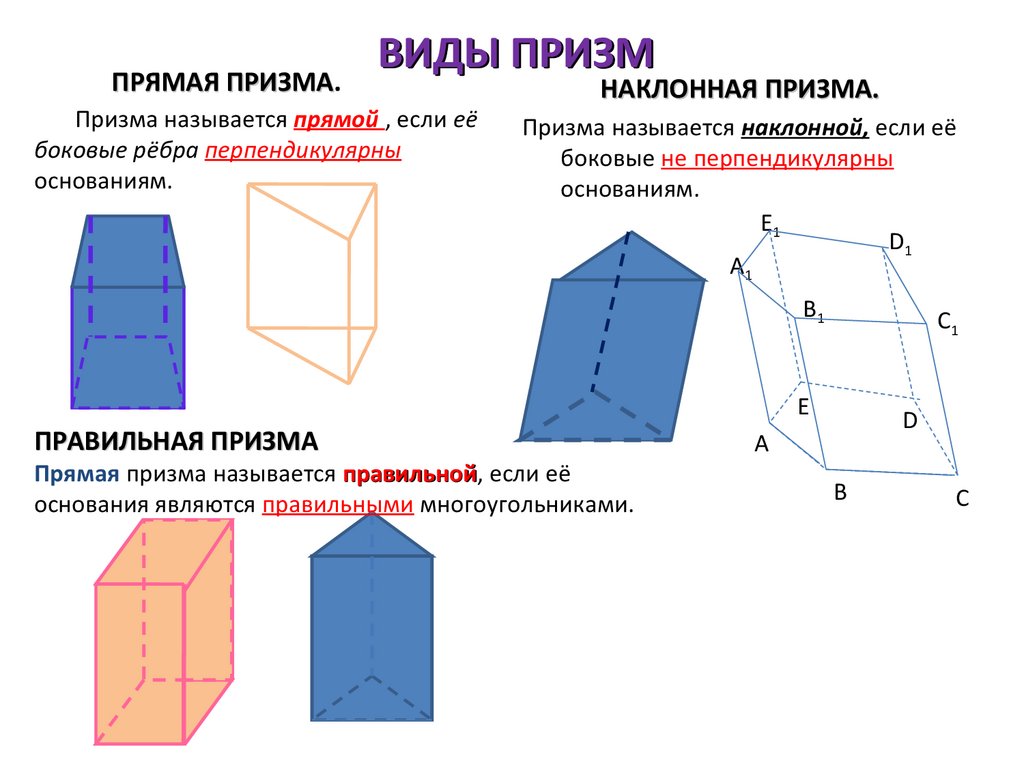
6. ПРЯМАЯ ПРИЗМА.
ПРИЗМАВИДЫ ПРИЗМ
Призма называется прямой , если её
боковые рёбра перпендикулярны
основаниям.
НАКЛОННАЯ ПРИЗМА.
Призма называется наклонной, если её
боковые не перпендикулярны
основаниям.
E1
D1
A1
B1
C1
E
ПРАВИЛЬНАЯ ПРИЗМА
Прямая призма называется правильной,
правильной если её
основания являются правильными многоугольниками.
D
A
B
C
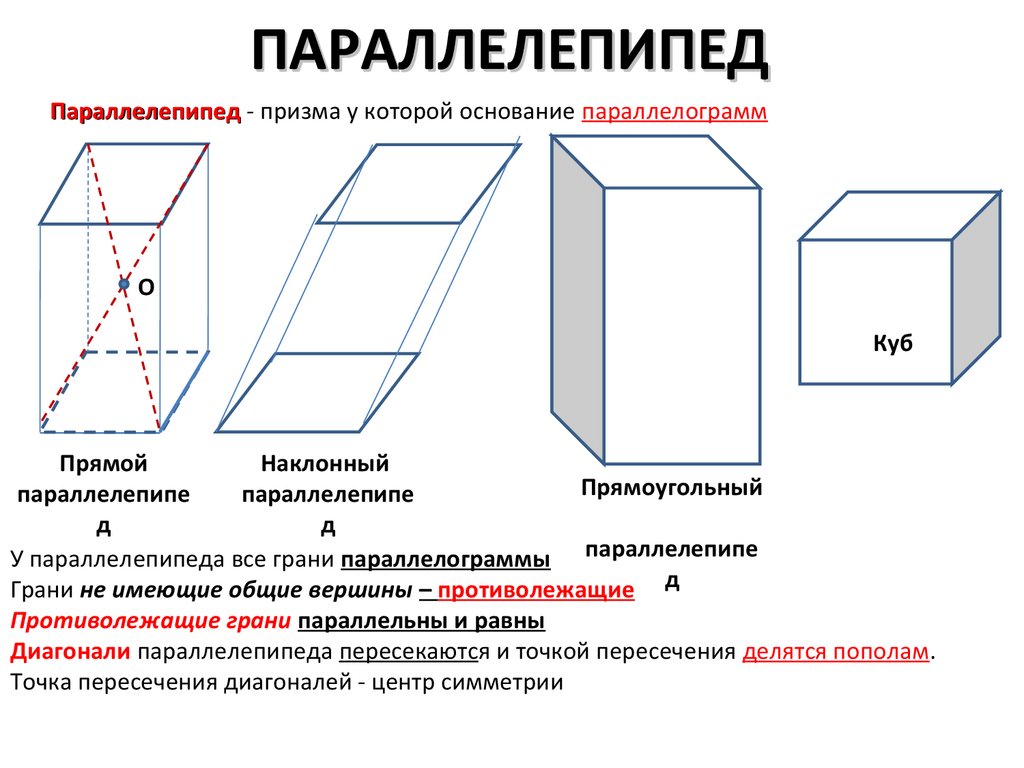
7. ПАРАЛЛЕЛЕПИПЕД
Параллелепипед - призма у которой основание параллелограммО
Куб
Прямой
Наклонный
Прямоугольный
параллелепипе
параллелепипе
д
д
У параллелепипеда все грани параллелограммы параллелепипе
Грани не имеющие общие вершины – противолежащие д
Противолежащие грани параллельны и равны
Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
Точка пересечения диагоналей - центр симметрии
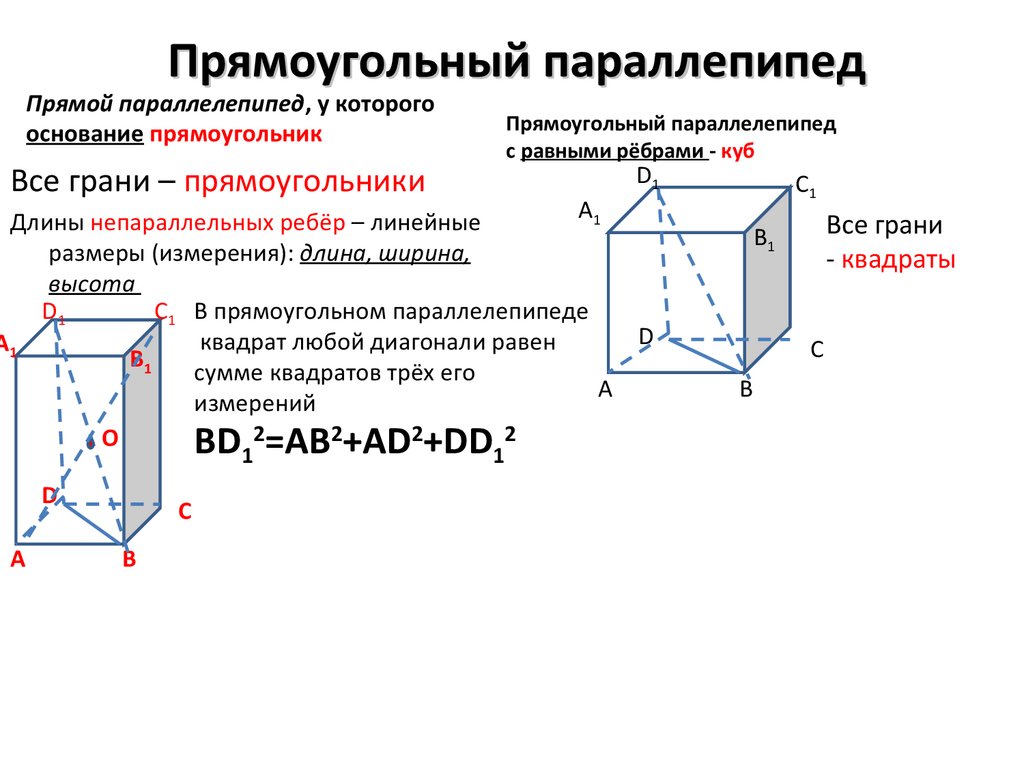
8. Прямоугольный параллепипед
Прямой параллелепипед, у которогооснование прямоугольник
Прямоугольный параллелепипед
с равными рёбрами - куб
D1
Все грани – прямоугольники
A1
Длины непараллельных ребёр – линейные
размеры (измерения): длина, ширина,
высота
D1
C1 В прямоугольном параллелепипеде
D
квадрат любой диагонали равен
A1
B1
сумме квадратов трёх его
A
измерений
О
BD 2=AB2+AD2+DD 2
1
D
A
C
B
1
C1
Все грани
- квадраты
B1
C
B

 mathematics
mathematics








