Призма. Элементы призмы

1.

Презентация на тему:
«Призма»

2.

Призма
Многогранник,
составленный из двух
равных многоугольников
A1A2…An и B1B2…Bn,
расположенных в
параллельных
плоскостях, и n
параллелограммов,
называется призмой
Bn
B1
B3
B2
An
A1
A3
A2

3.

Элементы призмы
Верхнее основание
Вершина
Боковое ребро
Боковая грань
Диагональ
Нижнее
основание
Высота

4.

• Равные многоугольники
A1A2…An и B1B2…Bn
называются основаниями
призмы,
а параллелограммы –
боковыми гранями
призмы

5.

Боковые ребра призмы
• Отрезки A1B1,
A2B2, … , AnBn
называются
боковыми
ребрами призмы
• Боковые ребра
призмы равны и
параллельны
Bn
B1
B3
B2
An
A1
A3
A2

6.

Высота призмы
Bn
B1
B3
B2
An
A1
M
A3
A2
• Перпендикуляр,
проведенный из
какой-нибудь точки
одного основания к
плоскости другого
основания,
называется высотой
призмы
B1M ( A1A2 A3 )

7.

Диагонали призмы
B1
C1
A1
D1
B
A
C
D
• Диагональю
призмы называется
отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

8.

Виды призм
Прямая призма
Правильная призма
Наклонная призма

9.

Виды призм
Шестиугольная
призма
Треугольная
призма
Четырехугольная
призма

10.

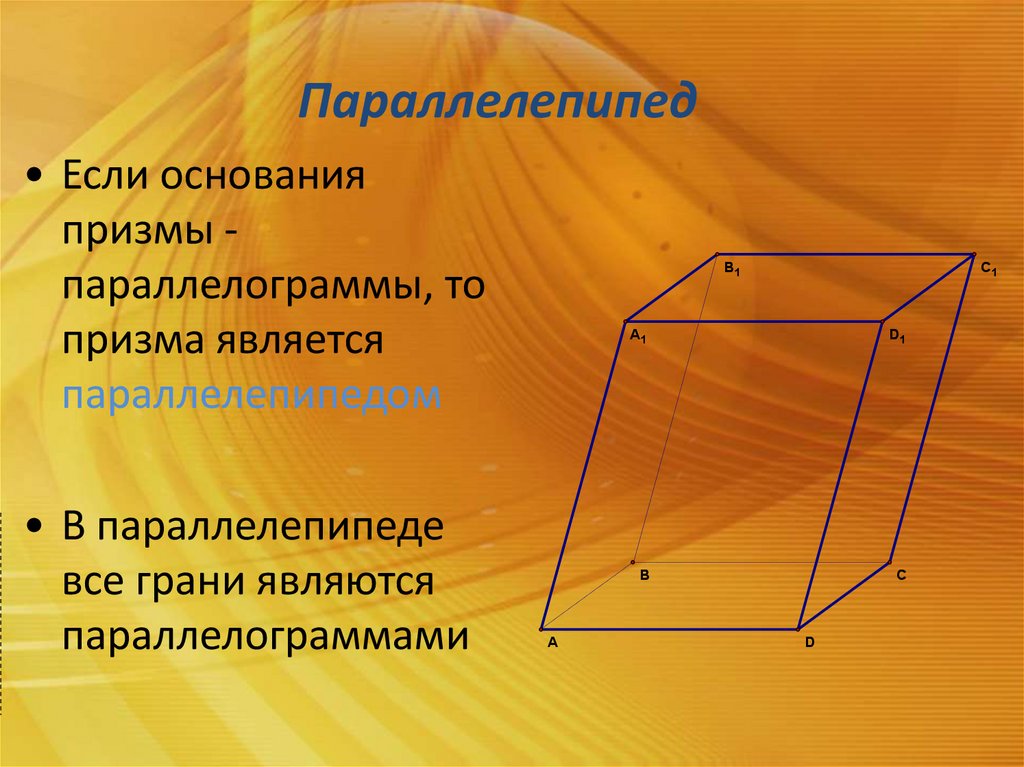
Параллелепипед
• Если основания
призмы параллелограммы, то
призма является
параллелепипедом
• В параллелепипеде
все грани являются
параллелограммами
C1
B1
A
A1
D1
B
C
D

11.

Прямая и наклонная призмы
• Если боковые ребра призмы перпендикулярны к
основаниям, то призма называется прямой,
• в противном случае – наклонной
• Высота прямой призмы равна её боковому ребру

12.

Правильная призма
Правильная призма — это прямая призма,
основанием которой является правильный
многоугольник. Боковые грани правильной
призмы — равные прямоугольники.

13.

Площадь поверхности призмы
• Площадью полной поверхности призмы
называется сумма площадей всех её
граней Sполн
• Площадью боковой поверхности призмы
называется сумма площадей её боковых
граней S
бок
Sполн Sбок 2Sосн

14.

Теорема о площади боковой
поверхности прямой призмы
Теорема.
Площадь боковой поверхности прямой
призмы равна произведению периметра
основания на высоту призмы
Sбок Pосн H

15.

Сечения призмы
• Диагональное
сечение – это
сечение
проходящее через
два боковых ребра,
не принадлежащих
одной грани.
• Перпендикулярное
сечение – это
сечение,
проходящее
перпендикулярно
боковым ребрам.

16.

Задача №1.
Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое
ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего основания и
противолежащую вершину нижнего основания.