Similar presentations:
Призма
1. ПРИЗМА
2.
Определение: многогранник, составленный издвух равных многоугольников A1A2…An и
B1B2…Bn, расположенных в параллельных
плоскостях, и n параллелограммов, называется
призмой.
Bn
B1
B3
B2
An
A1
A3
A2
Обозначение: A1A2…An B1B2…Bn - n угольная призма
3. Элементы призмы
BnB1
B3
B2
An
A1
A3
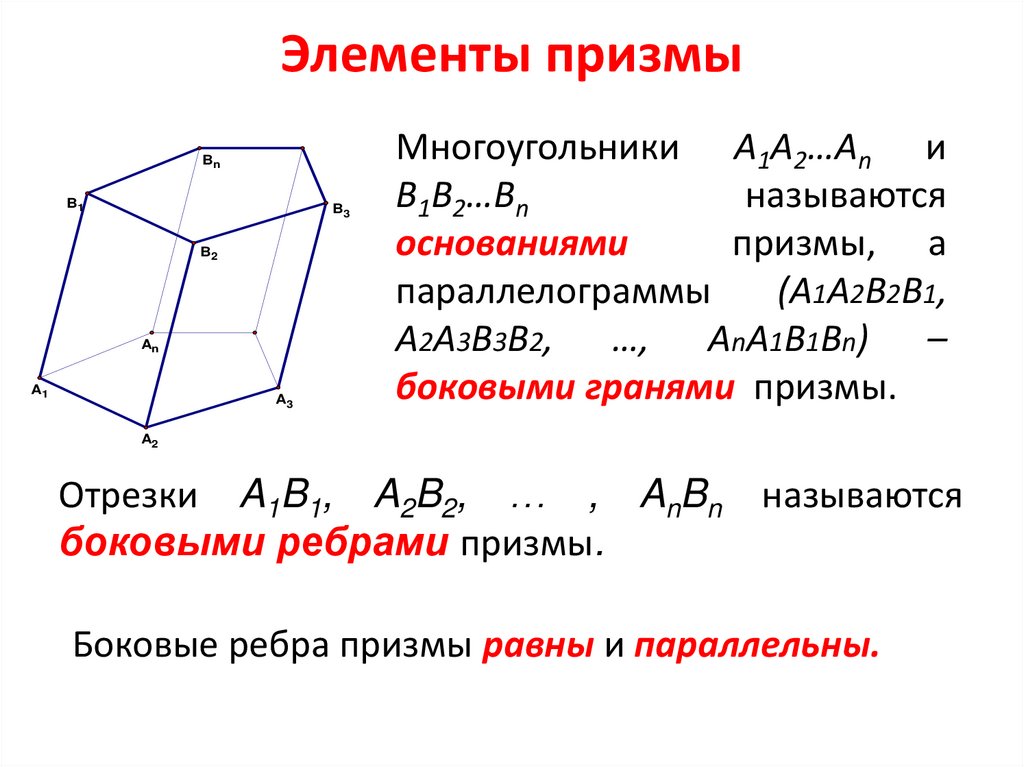
Многоугольники A1A2…An и
B1B2…Bn
называются
основаниями
призмы, а
параллелограммы
(А1А2В2В1,
А2А3В3В2, …, АnA1B1Bn) –
боковыми гранями призмы.
A2
Отрезки A1B1, A2B2, … , AnBn
боковыми ребрами призмы.
называются
Боковые ребра призмы равны и параллельны.
4.
BnB1
B3
B2
An
A1
Определение:
перпендикуляр,
проведенный из какойнибудь точки одного
основания к плоскости
другого основания,
называется высотой
призмы.
M
A3
A2
B1M ( A1A2 A3 )
5.
B1C1
A1
D1
B
A
C
D
Определение:
диагональю призмы
называется отрезок,
соединяющий две
вершины, не
принадлежащие одной
грани.
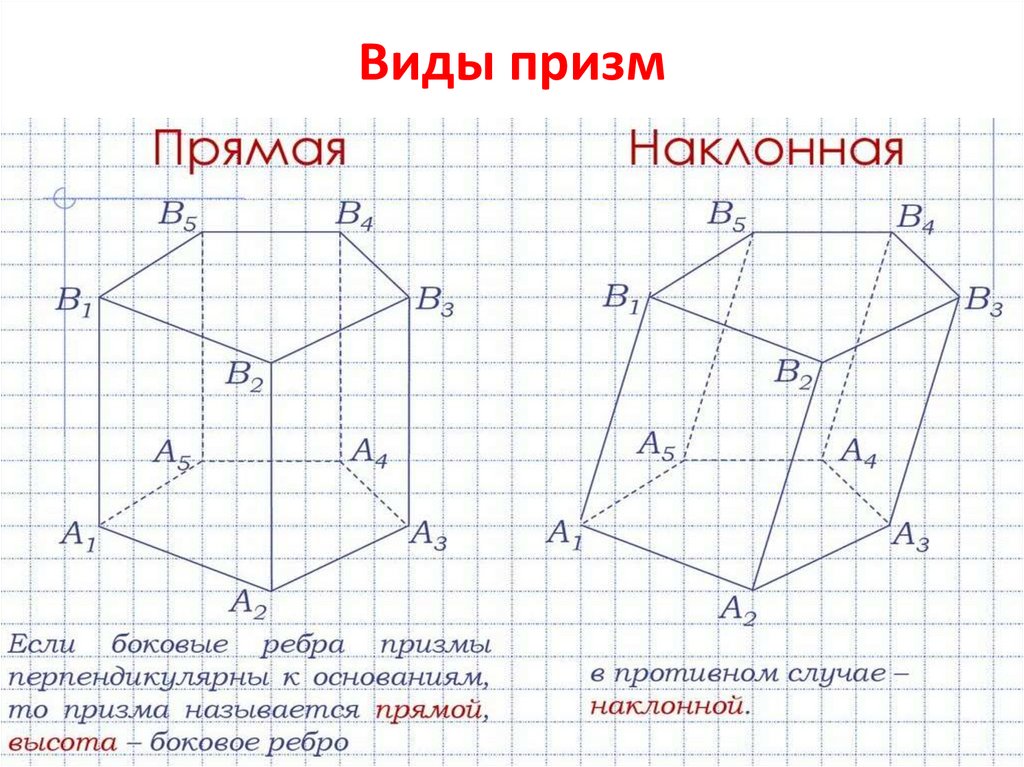
6. Виды призм
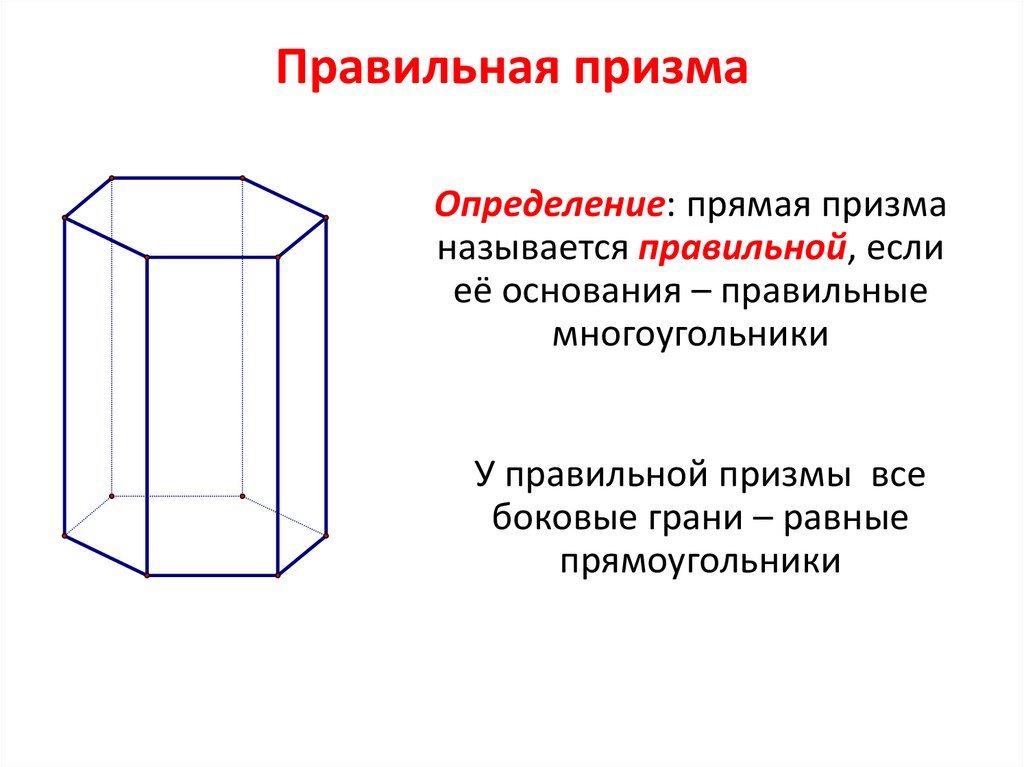
7. Правильная призма
Определение: прямая призманазывается правильной, если
её основания – правильные
многоугольники
У правильной призмы все
боковые грани – равные
прямоугольники
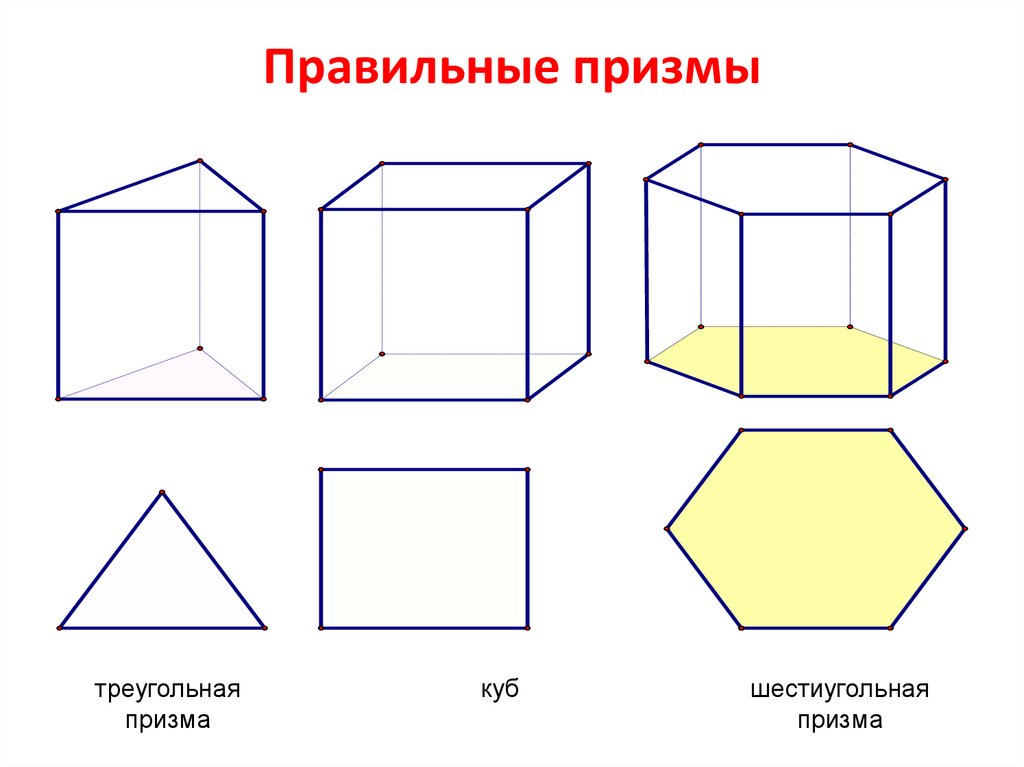
8. Правильные призмы
треугольнаяпризма
куб
шестиугольная
призма
9. Площадь поверхности призмы
Площадью полной поверхности ( Sполн ) призмыназывается сумма площадей всех её граней.
Площадью боковой поверхности ( Sбок ) призмы
называется сумма площадей её боковых граней.
Sполн Sбок 2Sосн
10. Теорема о площади боковой поверхности прямой призмы
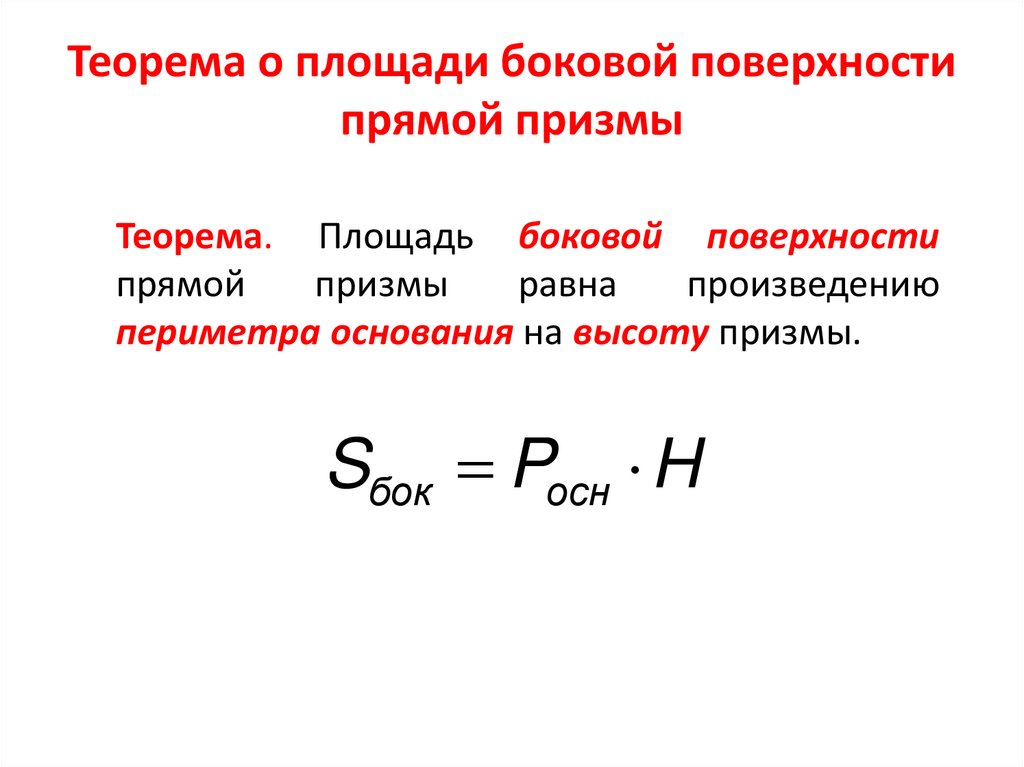
Теорема. Площадь боковой поверхностипрямой
призмы
равна
произведению
периметра основания на высоту призмы.
Sбок Pосн H






 mathematics
mathematics








