Similar presentations:
Классическая и релятивистская механика. Законы сохранения
1. Мультимедийные лекции по физике
Классическая ирелятивистская механика
2. Тема 5. ЗАКОНЫ СОХРАНЕНИЯ
План лекции5.1. Законы сохранения в классической механике.
5.2. Закон сохранения механической энергии.
5.3. Закон сохранения импульса.
5.4. Закон сохранения момента импульса.
3. 5.1. Законы сохранения в классической механике
В законах сохранения энергии, импульса, моментаимпульса находят своё отражение фундаментальные
свойства пространства и времени,
Закон сохранения энергии является следствием
однородности времени.
Закон сохранения импульса отражает однородность
пространства.
Закон сохранения момента импульса – отражает
изотропность пространства.
4.
Однородность времени отражает тот факт, чторезультат опыта не зависит от времени его
проведения.
Однородность пространства отражает тот факт, что
результат опыта не зависит от места его проведения.
Изотропность пространства отражает тот факт, что
результат опыта не зависит от направления осей
координат.
5.
Важно понять условия, при которых выполняется тотили иной закон сохранения.
Тела рассматриваемой механической системы могут
взаимодействовать как между собой, так и с
внешними телами.
Силы, с которыми тела системы взаимодействуют
между собой, называются внутренними.
6.
Силы, которые действуют на тела системы со сторонывнешних тел, называются внешними.
Механическая система называется замкнутой или
изолированной, если на нее не действуют внешние
силы (система не обменивается с внешними телами
энергией).
Понятие замкнутой системы является абстракцией.
7.
Реальным приближением к замкнутой системе служитсистема:
- взаимодействием которой с внешними телами можно
пренебречь;
- система, в которой внешние силы практически
компенсируются.
Система называется незамкнутой, если на неё
действуют внешние силы и их результирующая сила
отлична от нуля.
В любых системах сумма всех внутренних сил равна
нулю, поскольку силы взаимодействия каждой пары
тел равны по модулю и противоположны по
направлению.
8.
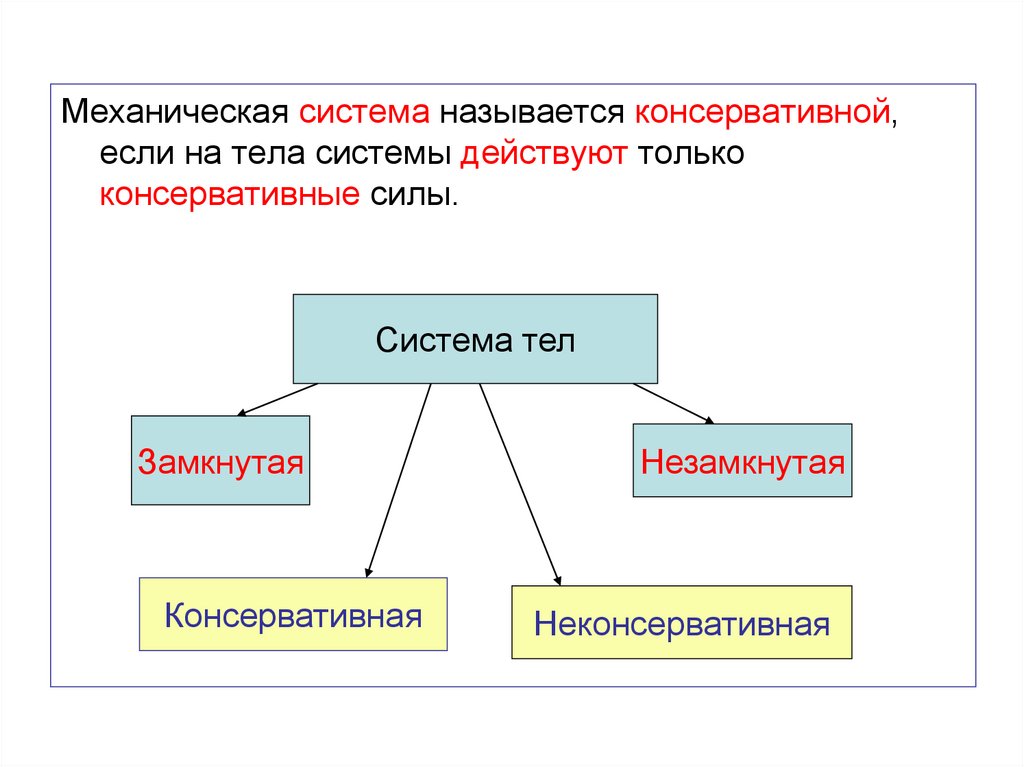
Механическая система называется консервативной,если на тела системы действуют только
консервативные силы.
Система тел
Замкнутая
Консервативная
Незамкнутая
Неконсервативная
9. 5.2. Закон сохранения механической энергии
Пусть тела (или точки) механической системывзаимодействуют как между собой, так и с внешними
телами.
Силы взаимодействия могут быть как
консервативными, так и неконсервативными.
Приращение кинетической энергии системы равно
работе всех действующих на систему сил.
10.
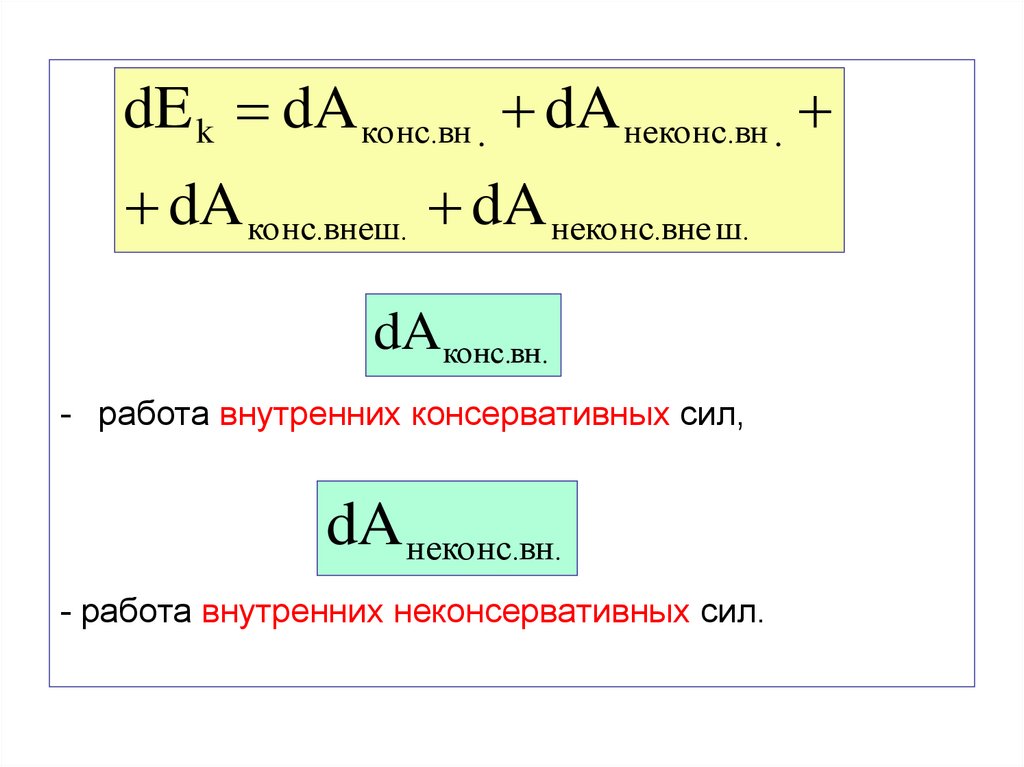
dE k dA конс.вн . dA неконс.вн .dA конс.внеш. dA неконс.вне ш.
dAконс.вн.
- работа внутренних консервативных сил,
dA неконс.вн.
- работа внутренних неконсервативных сил.
11.
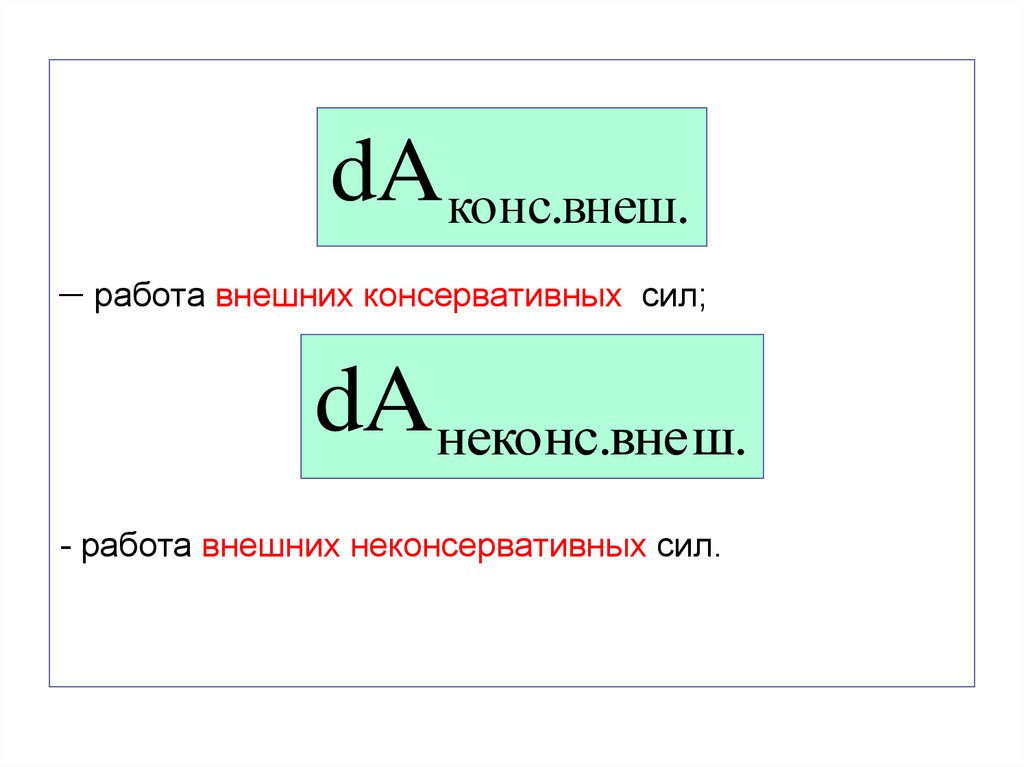
dA конс.внеш.– работа внешних консервативных
сил;
dAнеконс.вне ш.
- работа внешних неконсервативных сил.
12.
Работа внутренних консервативных сил равна убылипотенциальной энергии взаимодействия точек
системы друг с другом:
dAконс.вн dE п1
Работа внешних консервативных сил равна убыли
потенциальной энергии системы во внешних
потенциальных полях:
dA конс.внеш. dE п2
13.
Подставим это в уравнение для dEK и перенесем влевую часть.
dE K dE п1 dE п2
или
dA неконс.вн. dA неконс.вне ш.
d(E K E п1 E п2 )
dA неконс.вн. dA неконс.вне ш.
14.
Потенциальная энергия механической системы Eпскладывается из
- потенциальной энергии взаимодействия точек
системы друг с другом ЕП1;
- потенциальной энергии во внешних потенциальных
полях ЕП2:
E п Е п1 Е п2
Полная механическая энергия системы:
E EK Eп
Приращение полной механической энергии:
dE d(E K E п )
15.
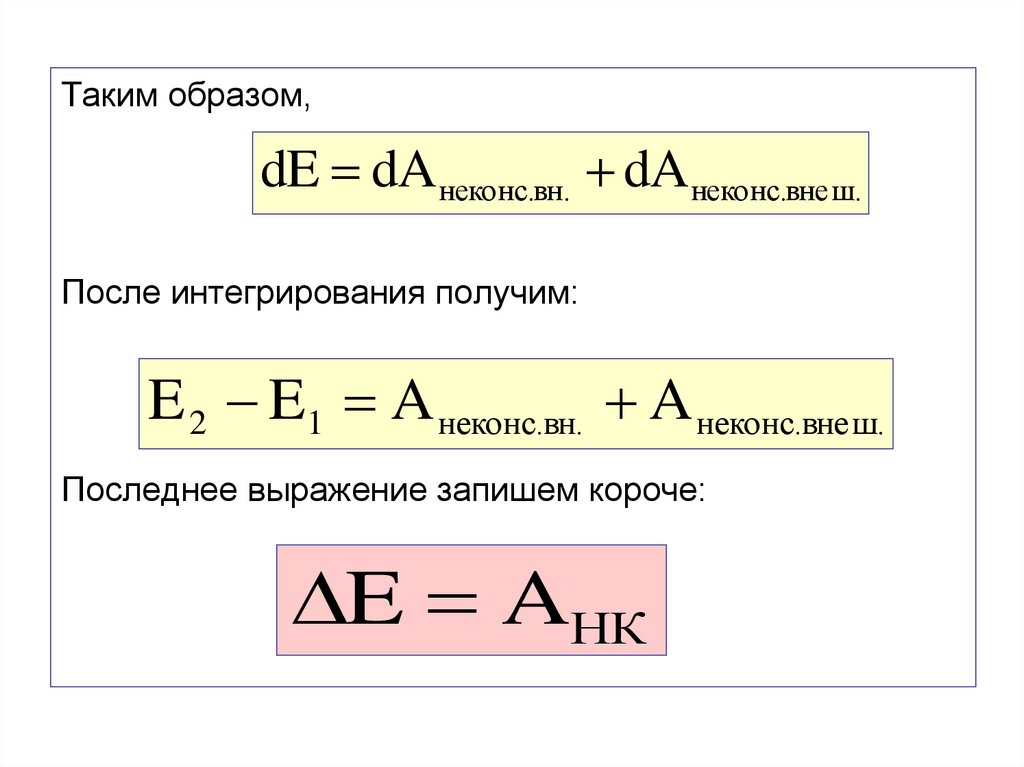
Таким образом,dE dAнеконс.вн. dAнеконс.вне ш.
После интегрирования получим:
E 2 E1 A неконс.вн. A неконс.вне ш.
Последнее выражение запишем короче:
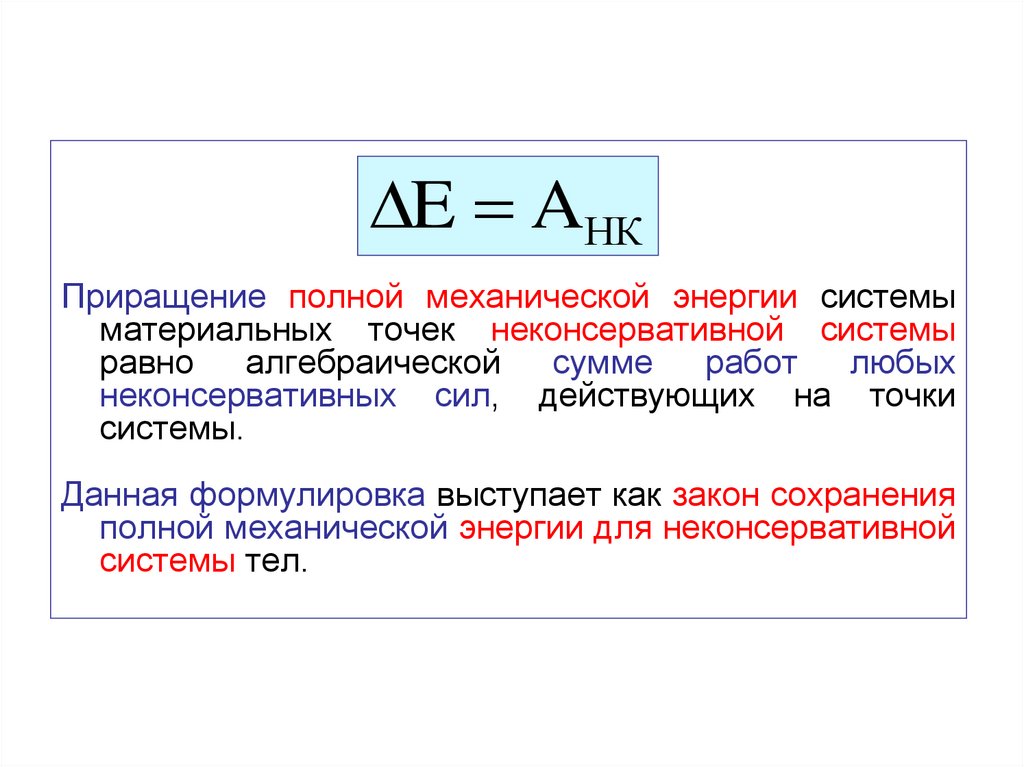
E AНК
16.
E AНКПриращение полной механической энергии системы
материальных точек неконсервативной системы
равно
алгебраической
сумме
работ
любых
неконсервативных сил, действующих на точки
системы.
Данная формулировка выступает как закон сохранения
полной механической энергии для неконсервативной
системы тел.
17.
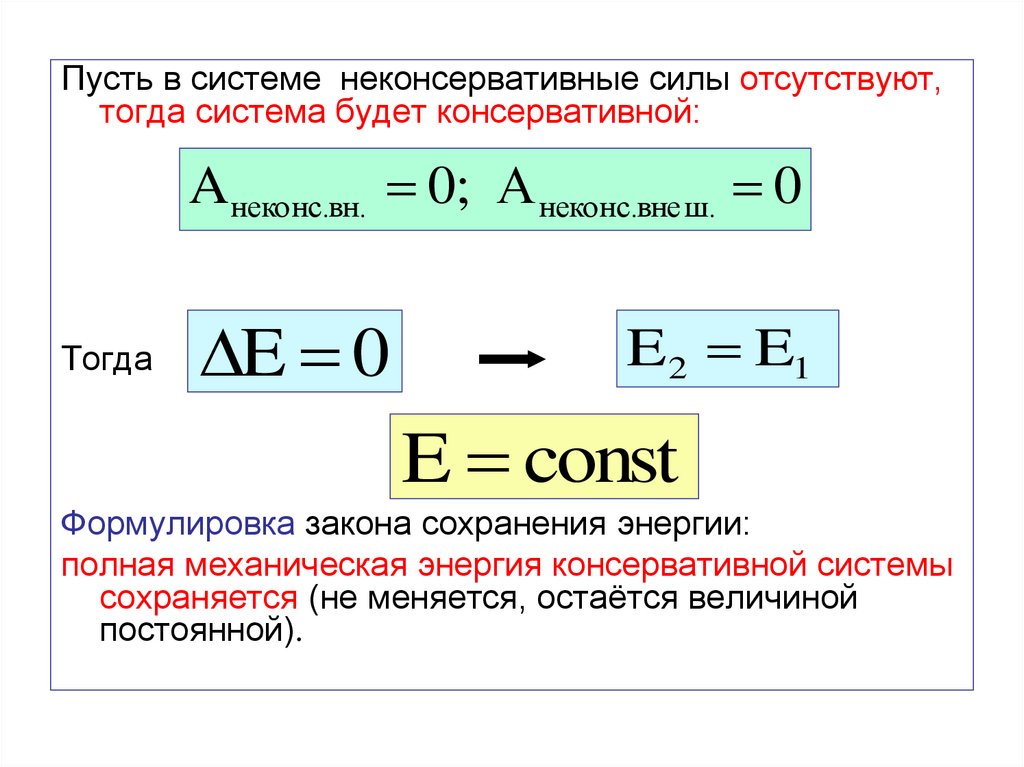
Пусть в системе неконсервативные силы отсутствуют,тогда система будет консервативной:
A неконс.вн. 0; А неконс.вне ш. 0
Тогда
E 0
E2 E1
E const
Формулировка закона сохранения энергии:
полная механическая энергия консервативной системы
сохраняется (не меняется, остаётся величиной
постоянной).
18. 5.2. Закон сохранения импульса
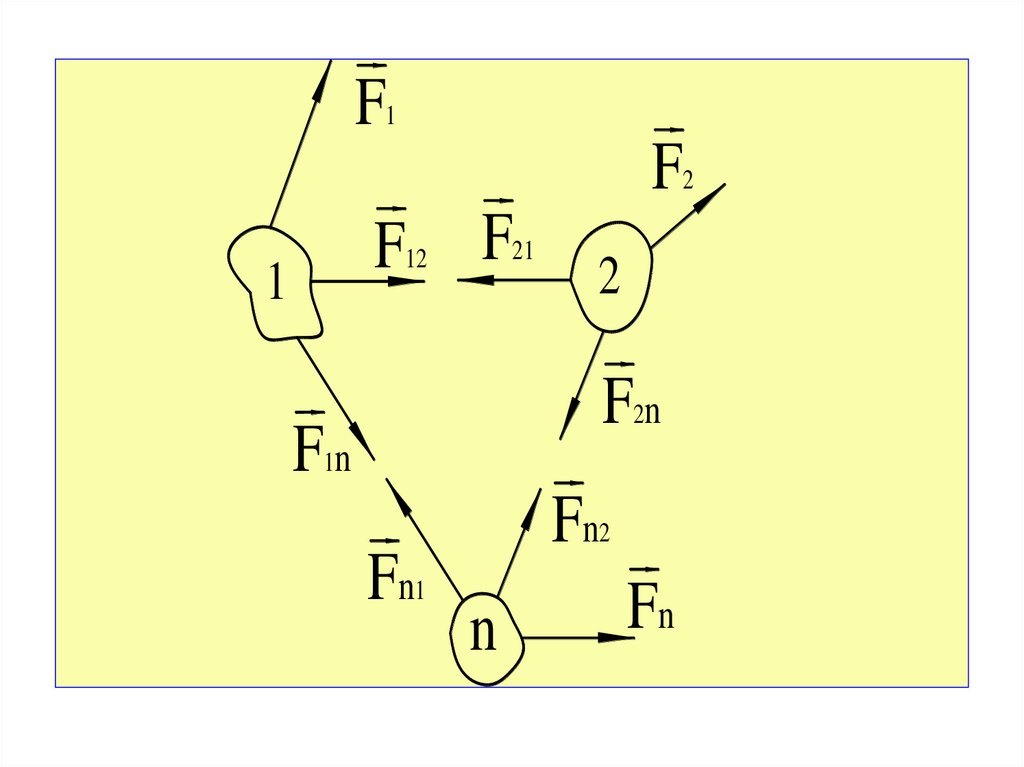
Рассмотрим механическую систему, состоящую из nтел, которые могут взаимодействовать как между
собой (это внутренние силы), так и с внешними
телами.
Силы взаимодействия могут быть как
консервативными, так и неконсервативными.
19.
F1F2
F12 F21 2
1
F2n
F1n
Fn1
Fn2
n
Fn
20.
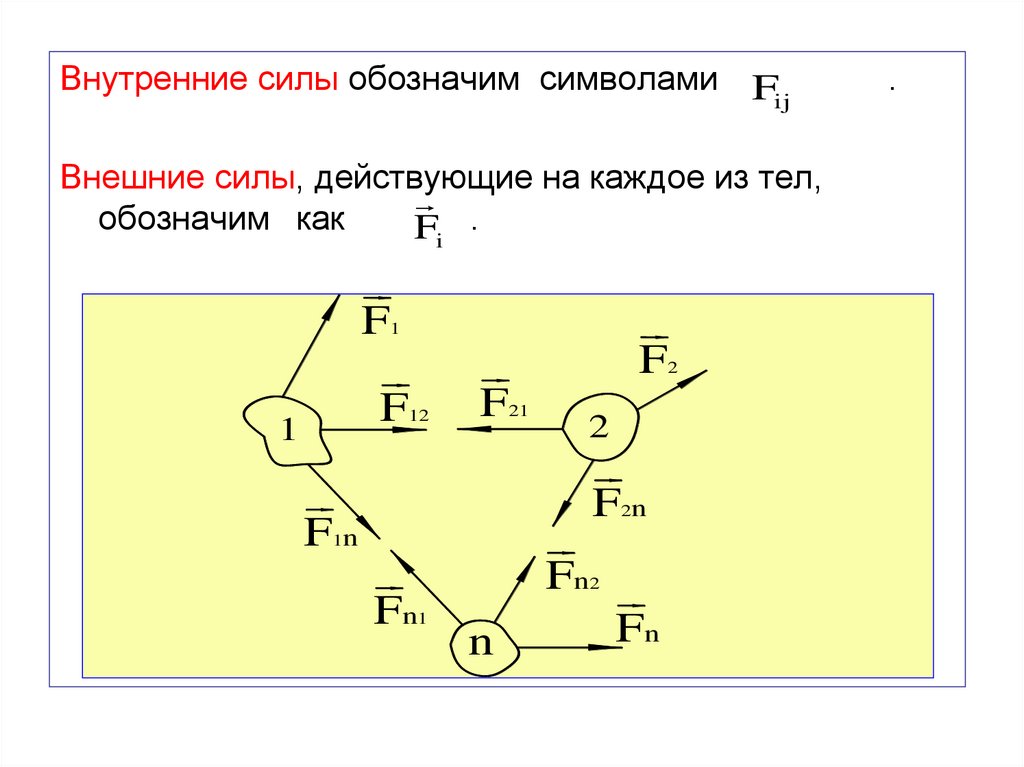
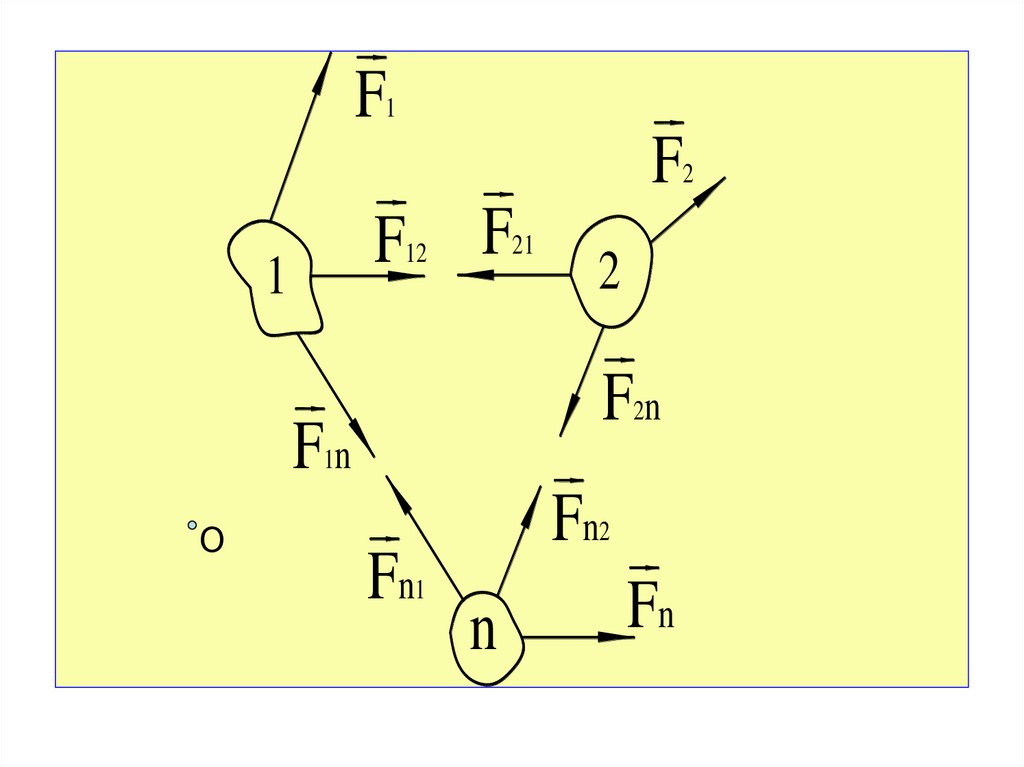
Внутренние силы обозначим символами Fij
Внешние силы, действующие на каждое из тел,
обозначим как
F .
i
F1
F2
F12
1
F21
2
F2n
F1n
Fn1
Fn2
n
Fn
.
21.
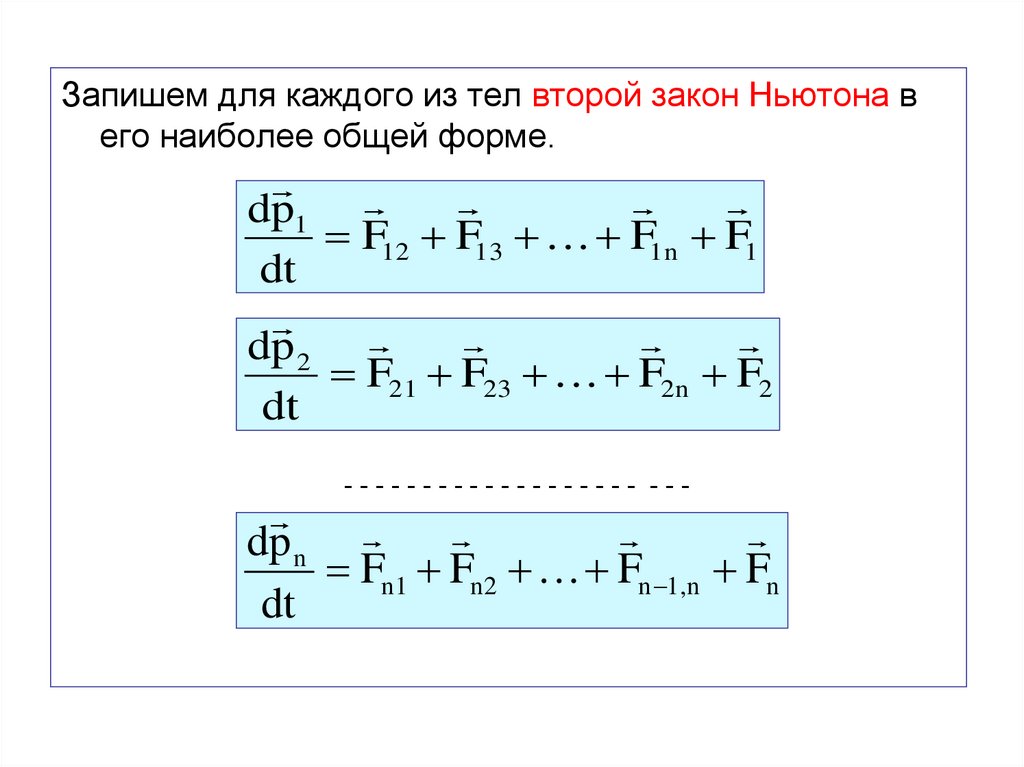
Запишем для каждого из тел второй закон Ньютона вего наиболее общей форме.
dp1
F12 F13 F1n F1
dt
dp 2
F21 F23 F2n F2
dt
------------------- ---
dp n
Fn1 Fn2 Fn 1,n Fn
dt
22.
Просуммируем левые и правые части равенств.По третьему закону Ньютона сумма всех внутренних
сил равна нулю, поскольку они попарно равны по
модулю и противоположны по направлению.
При сложении равенств получим следующее
выражение:
d
p1 p 2 p n F1 F2 Fn
dt
23.
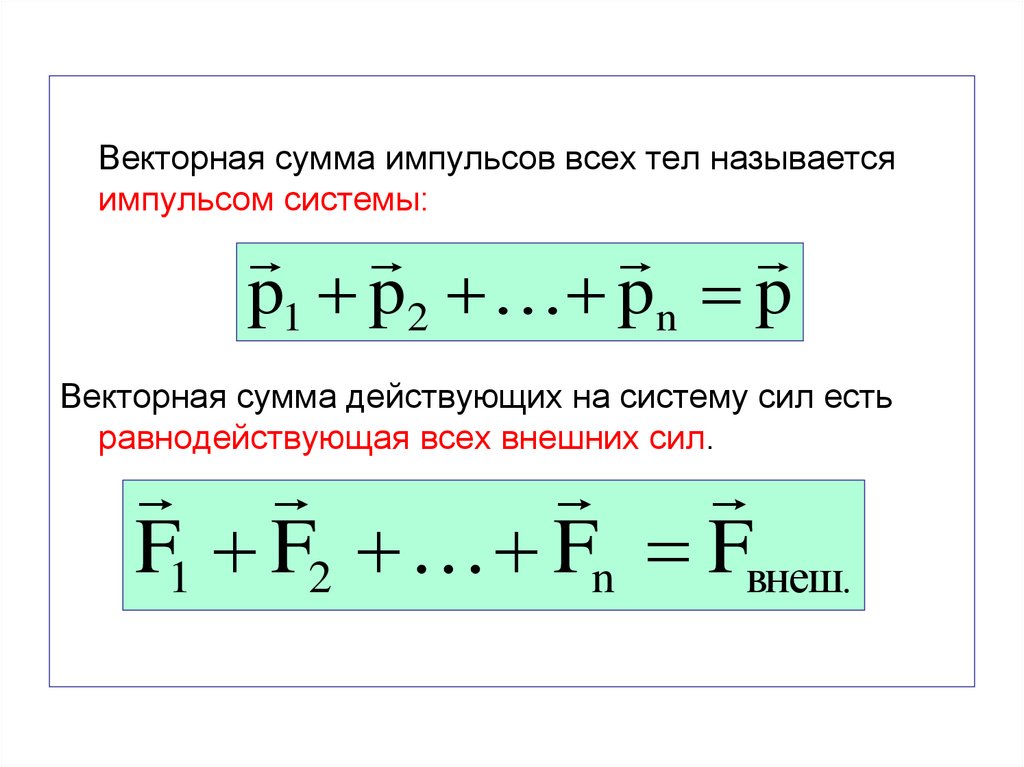
Векторная сумма импульсов всех тел называетсяимпульсом системы:
p1 p2 pn p
Векторная сумма действующих на систему сил есть
равнодействующая всех внешних сил.
F1 F2 Fn Fвнеш.
24.
Тогда можно переписатьdP
Fвнеш.
dt
Производная от полного импульса системы равна
равнодействующей всех приложенных к телам
системы внешних сил.
В незамкнутой системе тел скорость изменения
импульса системы равна равнодействующей
внешних сил (закон сохранения импульса для
незамкнутой системы тел).
Если система замкнута, то
Fвнеш. 0
25.
Тогдаdp
0
dt
P const
Формулировка закона сохранения импульса:
результирующий импульс замкнутой системы тел
сохраняется.
Естественно, что при этом остается постоянной и
сумма проекций импульсов тел системы на любую
координатную ось.
26.
На практике достаточно часто приходится иметь делосо взаимодействием тел в условиях, когда действием
внешних сил пренебречь нельзя (система не
замкнута).
В таких случаях можно найти такое направление
(координатную ось Х), на которое внешние силы
имеют нулевые проекции.
Тогда будет оставаться постоянной не векторная сумма
импульсов всех тел системы, а сумма проекций
импульсов на данную координатную ось.
PX = const.
27.
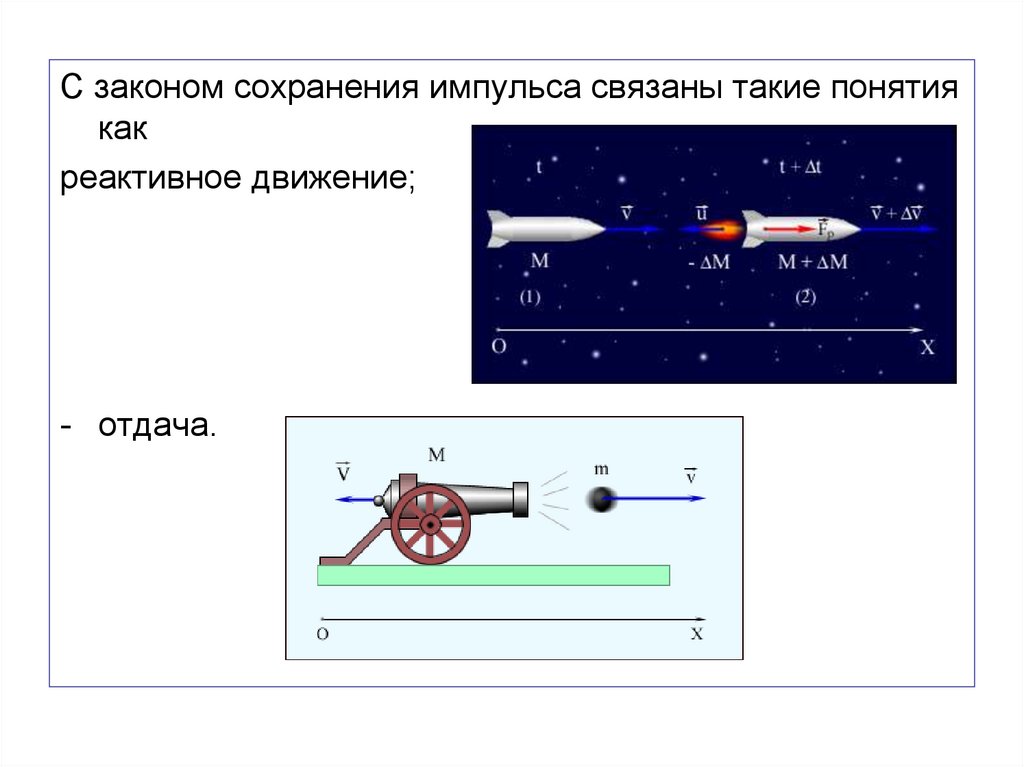
С законом сохранения импульса связаны такие понятиякак
реактивное движение;
- отдача.
28. 5.3. Закон сохранения момента импульса
Рассмотрим систему из n тел (или материальныхточек), взаимодействующих как между собой, так и с
внешними телами.
Выберем точку О, относительно которой будем
отсчитывать моменты импульсов частиц и моменты
сил, приложенных к ним.
29.
F1F2
F12 F21 2
1
F2n
F1n
О
Fn1
Fn2
n
Fn
30.
Изменение момента импульса каждой из частицсистемы обусловлено действием моментов
внутренних и внешних сил.
Согласно закону изменения момента импульса имеем:
dL1
M 12 M 13 M 1n M 1
dt
dL 2
M 21 M 23 M 2n M 2
dt
dL n
M n1 M n2 M n 1,n M n
dt
31.
Mi j– моменты внутренних сил, действующих
между i-ой и j-ой частицами ;
Mi
– моменты внешних сил, действующих на
i- ую частицу.
Сложим левые и правые части равенств:
d
L1 L 2 L n M1 M 2 M n
dt
Учтем, что сумма моментов внутренних сил равна нулю
32.
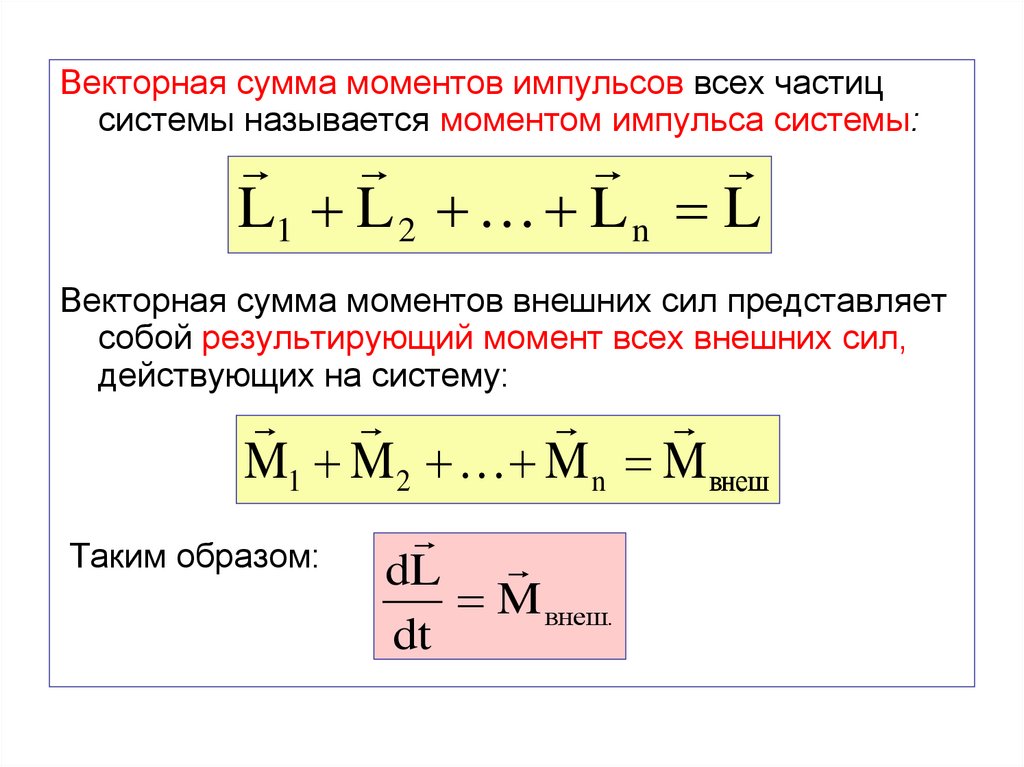
Векторная сумма моментов импульсов всех частицсистемы называется моментом импульса системы:
L1 L 2 L n L
Векторная сумма моментов внешних сил представляет
собой результирующий момент всех внешних сил,
действующих на систему:
M1 M 2 M n M внеш
Таким образом:
dL
M внеш.
dt
33.
dLM внеш.
dt
Производная от момента импульса по времени
незамкнутой системы по времени относительно
произвольной точки равна результирующему
моменту внешних сил относительно этой же точки.
В незамкнутой механической системе скорость
изменения результирующего момента импульса
равна равнодействующему моменту внешних сил.
34.
Если внешние силы отсутствуют или ихравнодействующая сила равна нулю, то система
будет замкнутой.
Тогда суммарный момент внешних сил относительно
произвольной точки О может быть равен нулю:
Mвнеш. 0
Следовательно
dL
0
dt
L const
Формулировка закон сохранения момента импульса:
результирующий момент импульса замкнутой
системы тел остается постоянным.
35.
Рисунок иллюстрирует закон сохранения моментаимпульса:
J1 1 J 2 2 J
, но
J1 1 (J1 J 2 )
2 0
36.
На практике часто приходится рассматриватьвращение взаимодействующих тел относительно
некоторой неподвижной оси Z.
В этом случае может сохраняться суммарный момент
импульса системы относительно данной оси Lz.
Необходимым условием этого является равенство
нулю суммарного момента внешних сил
относительно этой же оси вращения
M Z, ВНЕШ= 0.
Последнее может выполняться и для незамкнутой
системы, если внешние силы параллельны оси
вращения или пересекают эту ось.
37. Лекционная демонстрация № 7
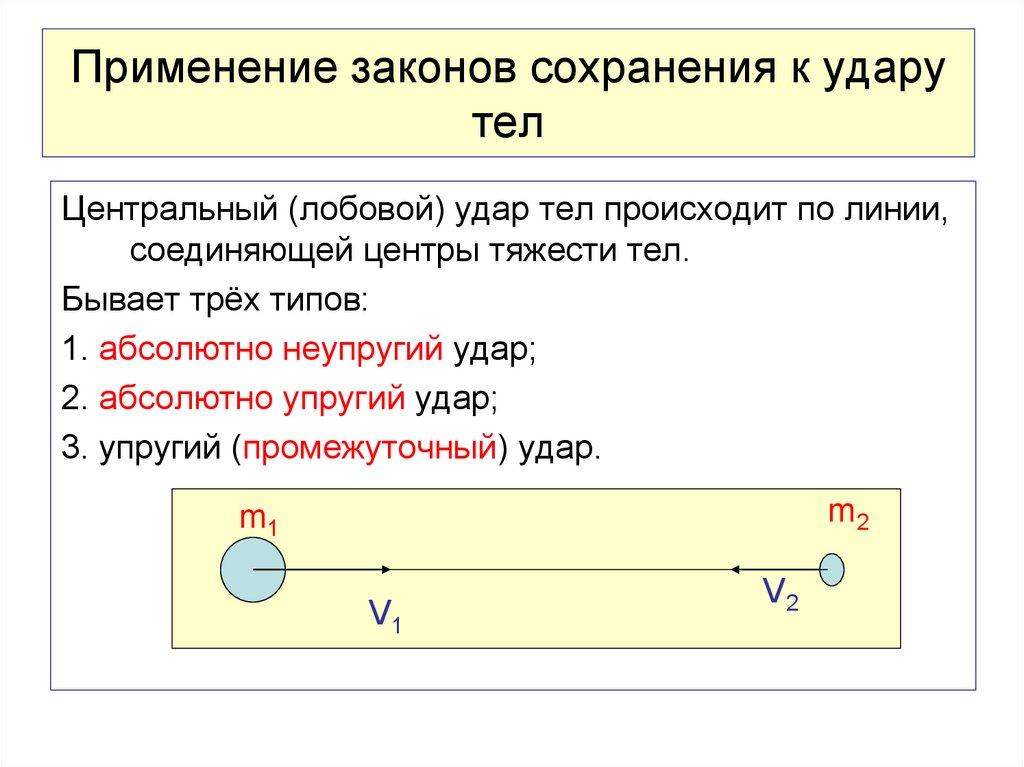
38. Применение законов сохранения к удару тел
Центральный (лобовой) удар тел происходит по линии,соединяющей центры тяжести тел.
Бывает трёх типов:
1. абсолютно неупругий удар;
2. абсолютно упругий удар;
3. упругий (промежуточный) удар.
m2
m1
V1
V2
39. Абсолютно неупругий удар
При абсолютно неупругом ударе тела:- деформируются;
- после удара движутся с одинаковыми скоростями.
При деформации часть кинетической энергии
превращается во внутреннюю энергию, поэтому
для этого удара сохраняется только импульс
системы тел.
m1V1 m 2 V2 (m1 m 2 ) V
mV
m 2 V2
(m1 m 2 )V 2
E ДЕФ
2
2
2
2
1 1
2
40.
Закон сохранения импульса в скалярной форме впроекциях на ось х:
m1
m1 m2
V1
V2
m2
до удара
V
после удара
х
m1V1 m2V2 (m1 m2 ) V.
41.
Закон сохранения энергии для абсолютно неупругогоудара тоже можно записать, но только с учётом той
энергии, которая перейдёт в другие виды энергии:
- энергию, ушедшую на деформацию тел;
- энергию, выделенную в виде тепла;
- энергию, ушедшую на трение и т.д.
m1V1 m 2 V2
(m1 m 2 )V
E
2
2
2
2
2
2
42. Лекционная демонстрация №3
43. Абсолютно упругий удар
При абсолютно упругом ударе тела:- не деформируются;
- после удара движутся с разными скоростями и
направлениями.
Для такого удара справедливыми являются два закона
сохранения: импульса
m1V1 m2V2 m1U1 m2 U 2
и энергии.
2
1
2
2
1
m1V
m 2 V2
m1U
m2U 2
2
2
2
2
2
44.
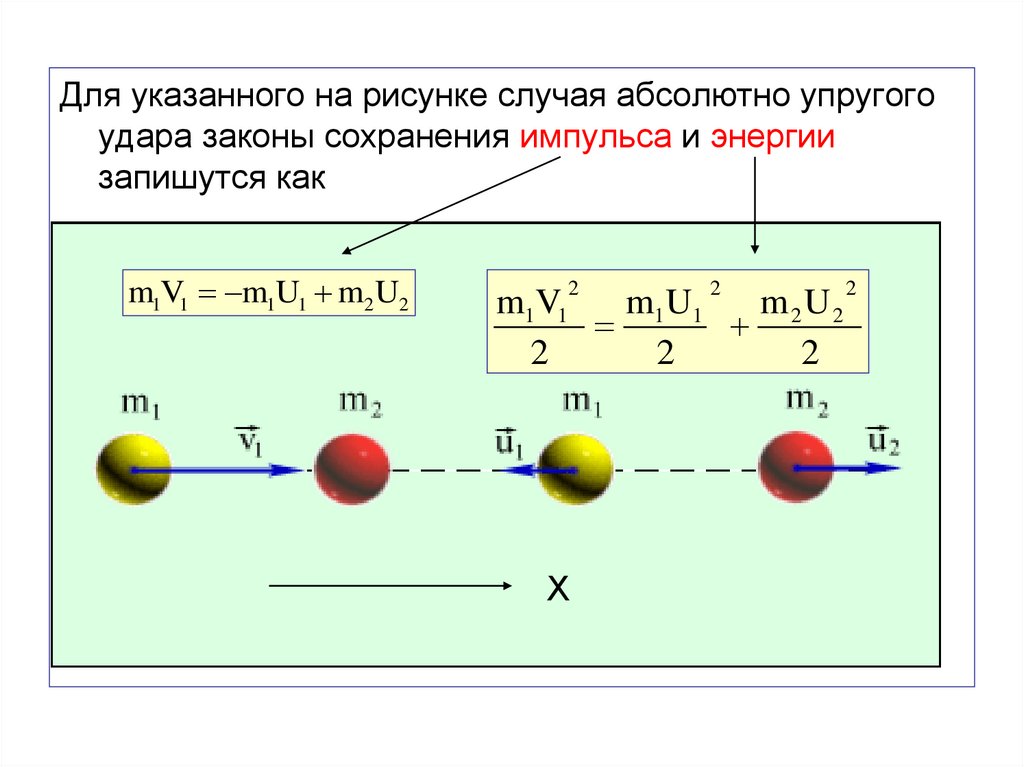
Для указанного на рисунке случая абсолютно упругогоудара законы сохранения импульса и энергии
запишутся как
m1V1 m1U1 m2 U2
2
2
m1V1
m1U1
m2U2
2
2
2
Х
2
45.
Рисунок иллюстрируетабсолютно упругий удар
шаров разной массы.
После удара изменились
направления движения
шаров.
При одинаковой массе
шаров получается игра
в билльярд.
46. Частные случаи
Сталкиваются шары массами m1 и m2.Скорости шаров до удара – V1 и V2.
Скорости шаров после удара – U1 и U2 .
Шары с одинаковыми массами (m1= m2)
обмениваются скоростями: U1 = V2 ; U2 = V1 .
2. Шары с одинаковыми массами (m1= m2), но второй
шар неподвижен (V2 = 0) – происходит обмен
импульсами: первый шар остановится, а второй
будет двигаться со скоростью первого(U2 = V1 ).
3. Столкновение шара со стеной (V2 = 0, m2 много
больше m1 ): U1 = -V1 .
1.
































 physics
physics








