Повторение курса геометрии за 8 класс

1.

Повторение курса геометрии
8 класса

2.

Содержание
1. Четырехугольники
• Многоугольники
• Параллелограмм и трапеция
• Прямоугольник, ромб, квадрат
2. Площадь
• Площадь многоугольника
• Площадь параллелограмма, треугольника и
трапеции
• Теорема Пифагора

3.

Содержание
3. Подобные треугольники
• Определение подобных треугольников
• Признаки подобия треугольников
• Соотношения между сторонами и углами
прямоугольного треугольника
4. Окружность
• Касательная к окружности
• Центральные и вписанные углы
• Вписанная и описанная окружности

4.

1. Четырехугольники
• Многоугольники
• Параллелограмм и трапеция
• Прямоугольник, ромб, квадрат

5.

C
D
E
B
F
A
G
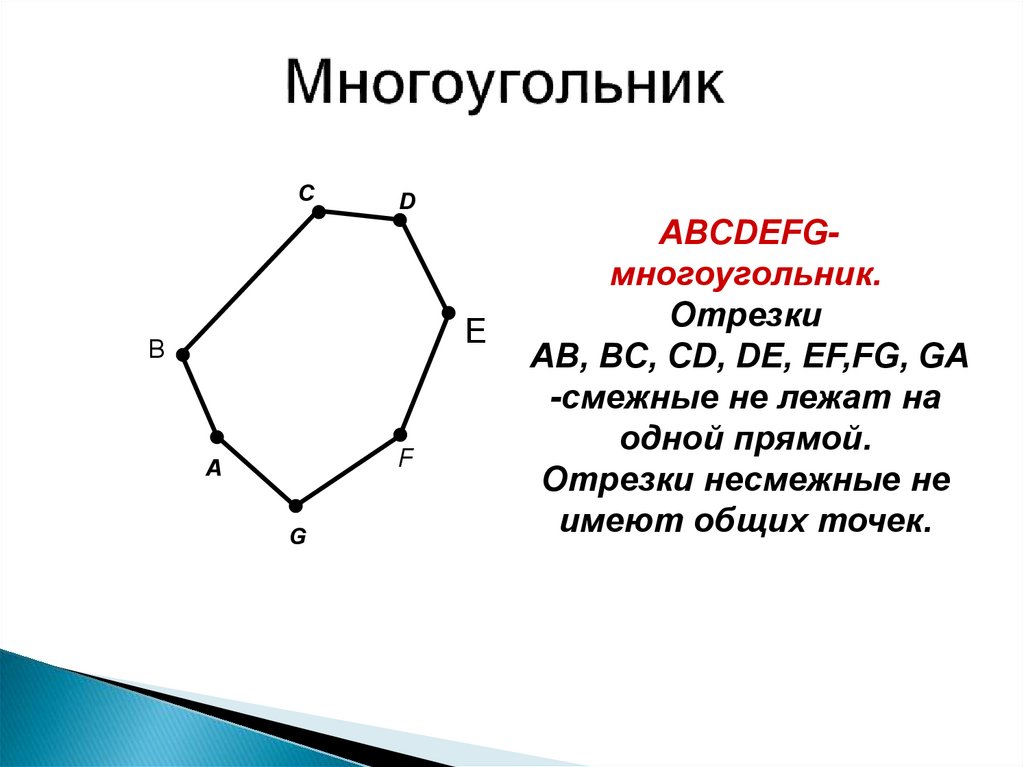
ABCDEFGмногоугольник.
Отрезки
AB, BC, CD, DE, EF,FG, GA
-смежные не лежат на
одной прямой.
Отрезки несмежные не
имеют общих точек.

6.

Многоугольник
C
D
E
B
F
A
G
A,B,C,D,E,F,Gвершины
многоугольника.

7.

C
D
E
B
F
А
G
AB, BC, CD, DE, EF, FG, GA
-стороны
многоугольника

8.

Многоугольник
C
D
E
B
Сумма длин сторон
AB, BC, CD, DE, EF, FG, GA
-называется
F
А
G
периметром многоугольника
Р=AB+ BC+ CD+ DE+ EF+ FG+GA

9.

Многоугольник
Многоугольник, имеющий n углов
называется n-угольником.

10.

Многоугольник
C
D
E
B
F
A
G
соседние вершины
-две вершины ,
принадлежащие
одной стороне

11.

Определение:
Отрезок, соединяющий две несоседние
вершины называется диагональю.
C
D
E
B
F
А
AC, AD, AE, AFдиагонали
многоугольника,
проведённые из
вершины А.
G
Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

12.

Определение:
Многоугольник называется выпуклым,
если он лежит в одной полуплоскости
относительно любой прямой,
содержащей его сторону.
Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - www.edu-reforma.ru

13.

Внешняя
область
Внутренняя
область

14.

Задача Сумма углов выпуклого многоугольника (п – 2)·180°
Сколько сторон имеет многоугольник, если каждый угол
которого равен 120°.
Решение
Обозначим п – количество вершин многоугольника.
Так как сумма углов выпуклого многоугольника
(п – 2) · 180°.
То следовательно (п – 2) · 180° = 120° · п
180° · п - 360° = 120° · п
60° · п = 360°
п = 360° : 60°
Ответ: 6 сторон.
30.11.2012
п=6
www.konspekturoka.ru
14

15.

Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция

16.

Параллелограмм

17.

Определение
А
D
В
С
Параллелограммэто
четырехугольник,
у которого
противоположные
стороны попарно
параллельны.
Если в четырехугольнике
ABIICD и BCIIAD, то
ABCD – параллелограмм.

18.

Свойства параллелограмма
А
D
В
C
1. В параллелограмме противоположные
стороны равны и противоположные
углы равны.
Если ABCD- параллелограмм, то
AD=BC, AB=CD, ∠A=∠C, ∠B=∠D.

19.

Свойства параллелограмма
А
В
O
D
C
2. Диагонали параллелограмма точкой
пересечения делятся пополам.
Если ABCD- параллелограмм, то
AO=OC, BO=OD.

20.

Если в задаче дано, что
четырехугольник –
параллелограмм,
то можно использовать
свойства параллелограмма.

21.

Признаки параллелограмма
А
D
В
C
1.Если в четырехугольнике противоположные
стороны
равны и параллельны, то это - параллелограмм.
Если ABIICD и AB=CD
ABCD Если ADIIBC и AD=BC параллелограмм

22.

Признаки параллелограмма
А
D
2.
В
C
Если в четырехугольнике
противоположные
стороны попарно равны, то это - параллелограмм.
Если AB=CD и AD=BC, то
ABCD -параллелограмм.

23.

Признаки параллелограмма
А
В
О
D
C
3.
Если в четырехугольнике
диагонали пересекаются
и точкой пересечения делятся пополам, то это параллелограмм.
Если AО=ОC и DО=ОB, то ABCD параллелограмм.

24.

Если в задаче нужно доказать,
что четырехугольник является
параллелограммом,
то применяют один из признаков
параллелограмма.

25.

Прямоугольник, его свойства и
признаки
2. Свойства
• Диагонали равны
BD = AC.
Обратное утверждение
1. Определение
Параллелограмм, у которого
все углы прямые.
А 90 ; В 90 ;
С 90 ; D 90 .
3. Признаки
• Если в параллелограмме
диагонали равны, то он
прямоугольник.

26.

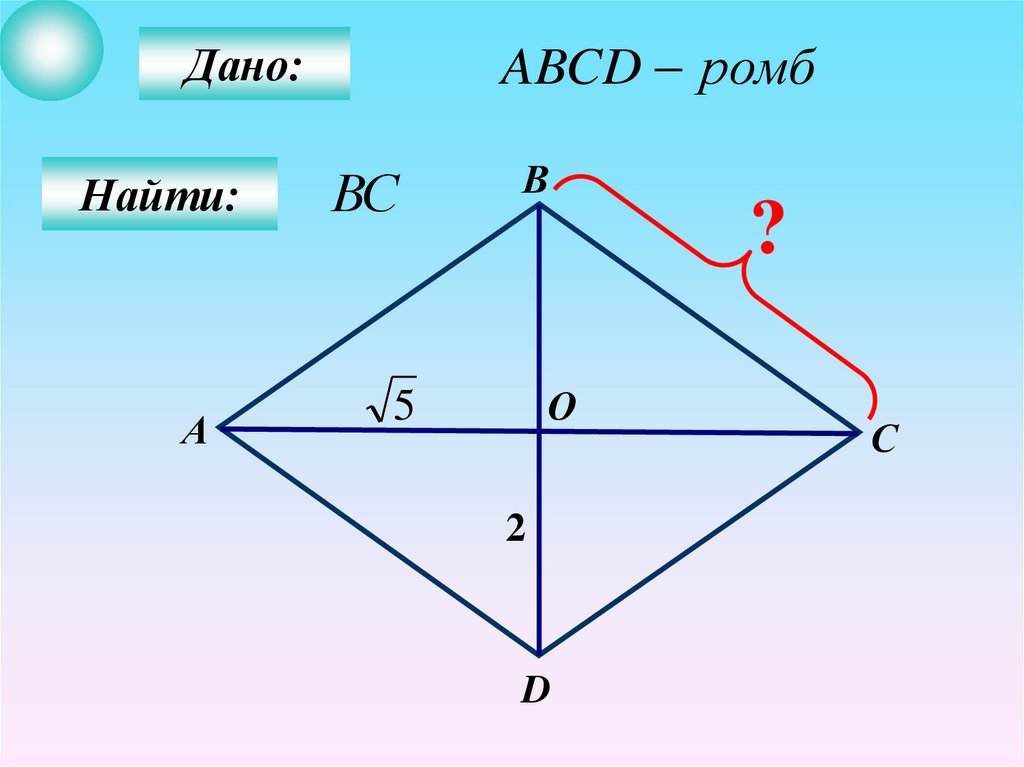
Ромб, его свойства и признаки
Свойства
• Диагонали взаимно
перпендикулярны и делят
углы пополам.
Определение
Параллелограмм, у которого
все стороны равны.
AB BC CD AD

27.

Квадрат, его свойства и признаки
Свойства
• Диагонали равны, взаимно
перпендикулярны , точкой
пересечения делятся пополам и делят
углы пополам.
• Признаки
Определение
Прямоугольник, у
которого все стороны
равны.
А 90 ; В 90 ; С 90 ; D 90 .
AB BC CD AD.
• Если в ромбе все углы равны, то он
квадрат.
• Если в ромбе диагонали равны, то он
квадрат.
AC BD , AC BD;
ВАО DAO; ВCO DCO;
ABO CBO; ADO CDO.

28.

Задача
В
C
Дано: ABCD – прямоугольник; CОD=60 .
600
O
A
Найти: АOB, BOC.
D
Ответ: АOB = 60 , BOC= 120 .

29.

Задача
Дано: ABCD – прямоугольник;
ABD больше СВD на 20°.
Найти: углы треугольника АОD.
Ответ: А = 35 , O= 110 , D = 35

30.

Задача
В ромбе угол между диагональю и
стороной равен 25 . Найдите углы
ромба.
Ответ: 50°;
130°

31.

Свойства площадей
1. Равные многоугольники имеют равные
площади.
2. Если
многоугольник
составлен
из
нескольких многоугольников, то его
площадь равна сумме площадей этих
многоугольников.
3. Площадь квадрата равна квадрату его
стороны.

32.

Площадь прямоугольника

33.

Площадь параллелограмма

34.

Площадь треугольника

35.

36.

Площадь трапеции

37.

1. Найти площадь прямоугольника ABCD, если
ВС=24, Р=72

38.

Теорема Пифагора
В
прямоугольном
треугольнике
квадрат длины гипотенузы равен
сумме квадратов длин катетов.