Similar presentations:
Вспомним геометрию 8 класса
1.
УМК: А.Г. Мерзляк и др.9 класс
2.
• Всё, что знаем о треугольниках• Всё, что знаем о четырёхугольниках
• Всё, что знаем про окружность и круг
3.
4.
• Треугольник и его элементы. Равные треугольники.• Высота, медиана, биссектриса треугольника.
• Признаки равенства треугольников
• Равнобедренный треугольник и его свойства.
• Равносторонний треугольник
• Признаки равнобедренного треугольника.
• Сумма углов треугольника. Внешний угол треугольника.
• Признаки равенства прямоугольных треугольников.
• Свойства прямоугольного треугольника.
• Средняя линия треугольника
5.
6.
треугольникиПо числу равных сторон
разносторонний
равнобедренный
равносторонний
В зависимости от величины углов
тупоугольный
остроугольный
прямоугольный
7.
Основные свойства треугольникаПризнак существования треугольника
(неравенство треугольника):
АВ < ВС+АС
ВС < АВ+АС
АС < АВ+ВС
В
Свойство углов треугольника:
180 0
А
С
D
Внешний угол треугольника равен сумме внутренних,
не смежных с ним
8.
БиссектрисаВспомните определение биссектрисы угла.
(Луч, выходящий из вершины угла и делящий его на два равных угла,
называется биссектрисой угла)
Постройте биссектрису BK угла B с помощью транспортира. Она
пересечёт отрезок AC в точке K.
Отрезок BK называется биссектрисой угла B треугольника ABC.
Биссектрисой треугольника называется отрезок биссектрисы угла
треугольника, соединяющий вершину угла треугольника с точкой
противоположной стороны треугольника.
9.
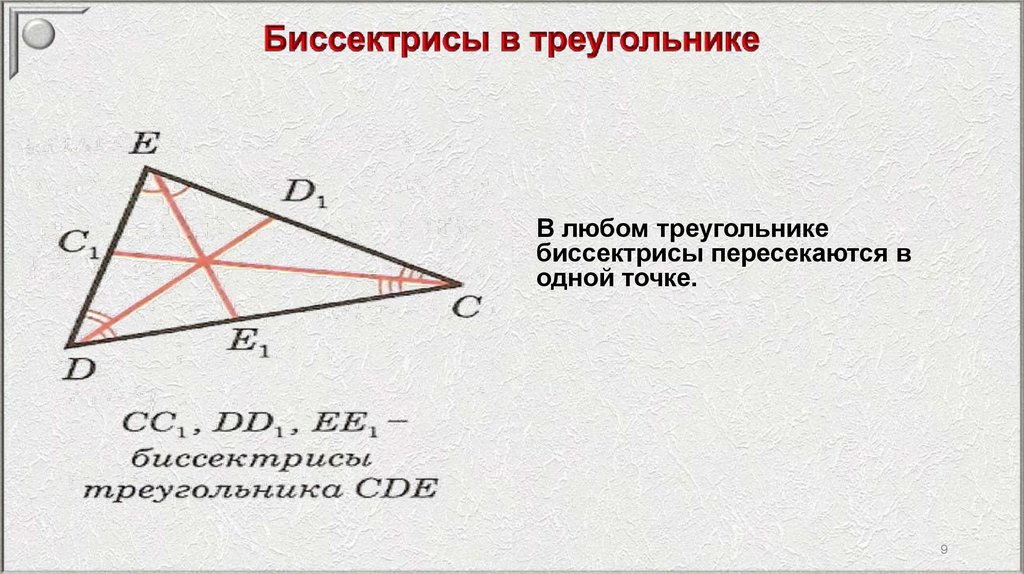
В любом треугольникебиссектрисы пересекаются в
одной точке.
9
10.
Медиана1. Начертите треугольник АBС и найдите
середину отрезка стороны ВС – точку N.
2. Соедините точку N с вершиной A.
Отрезок AN называется медианой
треугольника
Что называется серединой отрезка?
(Серединой отрезка называется точка отрезка, которая
делит его пополам, то есть делит на два равных
отрезка).
Медианой треугольника называется
отрезок, соединяющий вершину треугольника с серединой
противоположной стороны.
11.
(3)Сколько вершин у треугольника?
Сколько у него сторон?
(3)
Сколько медиан можно провести в треугольнике?
Какое свойство вы заметили?
Начертите произвольный треугольник и
проведите три медианы.
(3)
12.
ВысотаС помощью чертёжного угольника из
вершины С треугольника АСВ проведём
перпендикуляр CD к прямой AB. Этот
отрезок называется высотой треугольника.
Высотой треугольника называется перпендикуляр, проведённый из
вершины треугольника к прямой, содержащей противолежащую сторону.
Замечание: высота может выходить
за пределы треугольника
13.
Высоты или их продолженияпересекаются в одной точке.
Эта точка называется ортоцентром.
Центр тяжести треугольника, его ортоцентр
и точка пересечения биссектрис треугольника
называются (особыми) замечательными точками
треугольника.
13
14.
Свойства р/б треугольника.• В равнобедренном треугольнике биссектриса, проведённая к
основанию, является медианой и высотой.
• Углы при основании равнобедренного треугольника равны.
Если в треугольнике два угла равны, то он
равнобедренный.
• Если в треугольнике медиана является и высотой, то
такой треугольник равнобедренный.
15.
Треугольник, у которого все стороны равны, называетсяравносторонним.
А
В
С
Любой равносторонний треугольник является
равнобедренным.
16.
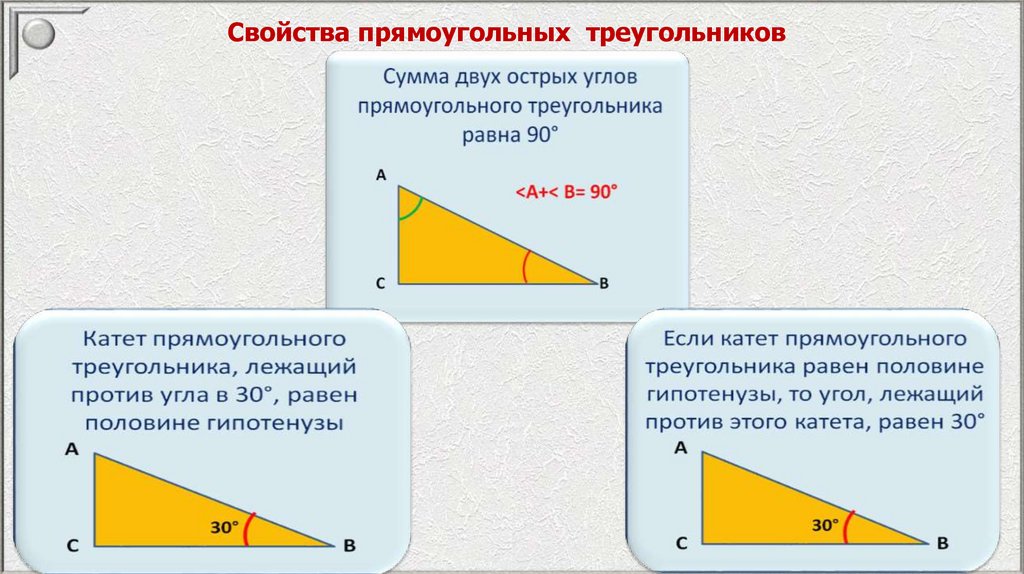
Свойства прямоугольных треугольников17.
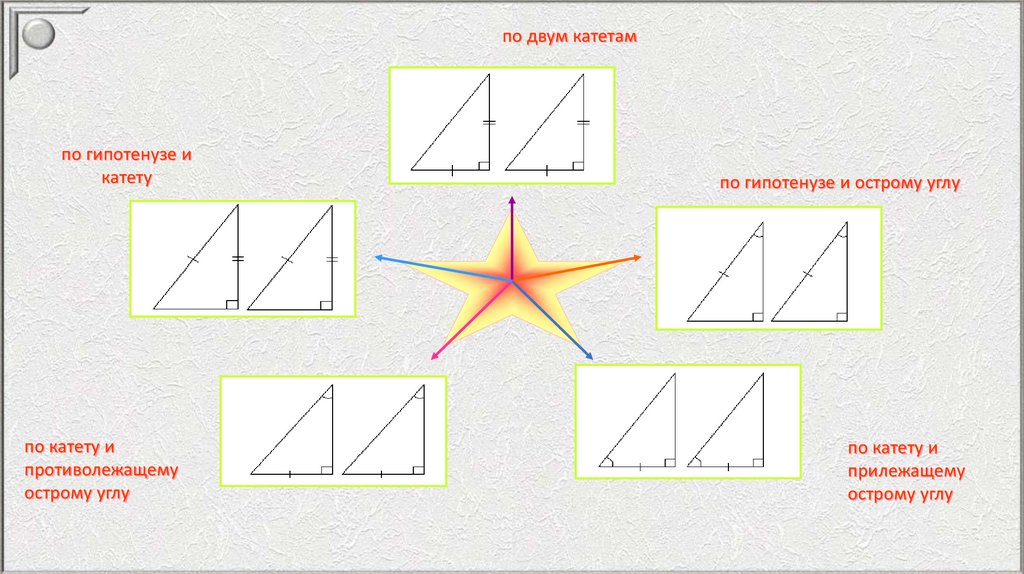
по двум катетампо гипотенузе и
катету
по катету и
противолежащему
острому углу
по гипотенузе и острому углу
по катету и
прилежащему
острому углу
18.
Определение. Средней линией треугольника называется отрезок, соединяющийсередины двух его сторон.
С
А
В
Сколько средних линий можно построить в треугольнике?
Теорема 7.1. Средняя линия треугольника параллельна одной из его сторон и равна
половине этой стороны.
19.
1. В треугольнике два угла равны 72° и 42°. Найдите его третий угол.2. В ∆ ABC C =115°. Найдите внешний угол при вершине C.
3. В ∆ ABC известно, что BAC = 68°, AD – биссектриса. Найдите BAD.
4. В ∆ ABC известно, что АС =14 , BM – медиана, BM =10 . Найдите АM.
5. Точки M и N являются серединами сторон AB и BC ∆ ABC, AB =21, BC=22, AC=28.
Найдите MN.
6. Точки M и N являются серединами сторон AB и BC ∆ ABC соответственно. Отрезки
AN и CM пересекаются в точке O, AN = 27, CM=18. Найдите CO.
7. В ∆ DЕР проведена биссектриса ЕК. Найдите стороны DЕ и ЕР,
если DК=3см, КР=4см, а периметр ∆ DЕР равен 21см.
8. Катеты прямоугольного треугольника относятся как 3 : 4, гипотенуза равна 20см.
Найдите площадь этого треугольника.
9. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.
10. В треугольнике ABC угол C равен 90°, M – середина стороны AB, AB = 26, BC =18.
Найдите CM.
20.
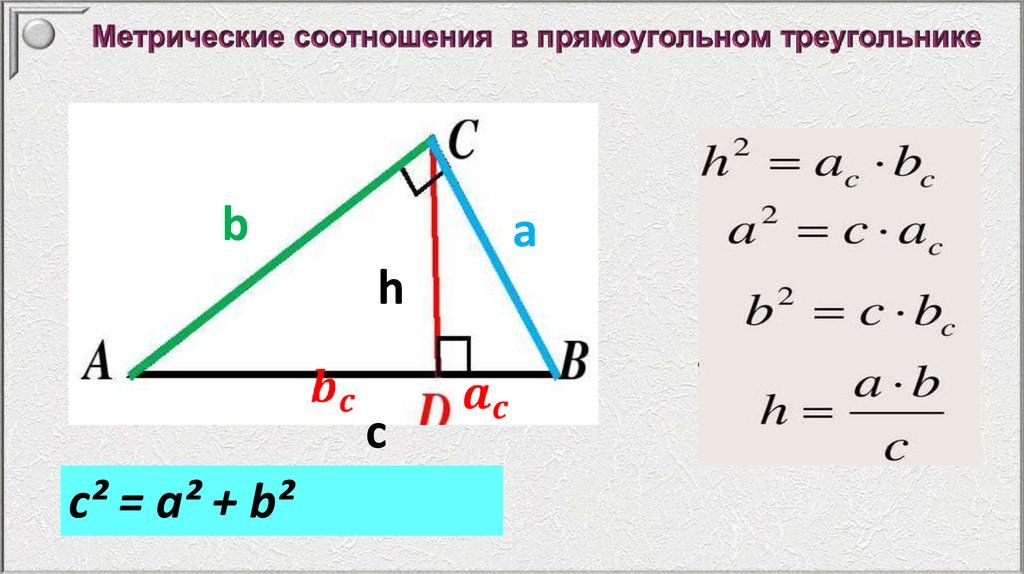
• Подобие треугольников• Метрические соотношения в прямоугольном
треугольнике
• Теорема Пифагора
• Решение прямоугольных треугольников
• Площадь треугольника
21.
1. Какие треугольники называются подобными?2. Сформулировать теорему об отношении площадей треугольников,
имеющих по равному углу.
3. Два треугольника подобны. Два угла одного треугольника 1200 и
500. Чему равен меньший угол второго треугольника?
Ответ: 100
4. У подобных треугольников сходственные стороны равны 3см и
9см. Площадь первого треугольника равна 8 см2. Найдите площадь
второго треугольника.
Ответ: 72 см2
22.
BА
Определение подобных треугольников
Два треугольника называются подобными,
если их углы соответственно равны и
стороны
одного
треугольника
пропорциональны сходственным сторонам
С другого.
B1
С1
А1
A A1 ,
AB
BC
CA
A1 B1
B1C1
C1 A1
ABC
k
A1 B1C1
B B1 , C C1
- коэффициент подобия
23.
Отношение площадей двух подобныхтреугольников равно квадрату
коэффициента подобия.
В
А
М
С
Р
Отношение периметров двух подобных
треугольников равно коэффициенту
подобия.
К
где k – коэффициент подобия.
S ABC
k2
S MPK
Р ABC
k
РMPK
24.
ТеоремаЕсли угол одного треугольника равен углу другого треугольника, то площади
этих треугольников относятся как произведения сторон, заключающих равные
углы.
С
S ABC
AB AC
S A1B1C1
A1 B1 A1C1
С1
Это свойство площадей поможет нам доказать
первый признак подобия треугольников.
А
В
А1
В1
25.
Теорема 13.1Если два угла одного треугольника соответственно равны двум углам
другого треугольника, то такие треугольники подобны.
Теорема 14.1
Если две стороны одного тр-ка пропорциональны двум сторонам другого
тр-ка и углы, заключенные между этими сторонами, равны, то такие тр-ки
подобны.
Теорема 14.2
Если три стороны одного треугольника пропорциональны трем сторонам
другого треугольника , то такие треугольники подобны.
26.
АВСD – параллелограмм. Найдите пары подобных треугольников идокажите их подобие. Найти ВС.
А С ,
ABK CBE
ВКА ВЕС
по 1 признаку
С
B
CB
BK
=
BE
9
10
Е
A
BA
6
К
1
D
10
CB
6
=
9
=
AK
CE
27.
Найдите пары подобных треугольников и докажите их подобие.4
ВОС АОD , 12
AОD
4
=
С
5
O
15
A
12
21
15
COD по 2 признаку
?7
B
5
D
28.
Доказать: КМ II BL7
B
14
5
=
10
3
=
6
KMA
LBC
по 3 признаку
10
14
M
C
5
6
7
L
A
3
K
S AMK 1
;
4
S CBL
Найти
Р AMK 1
2
РCBL
29.
ЛеммаВысота в прямоугольном треугольнике, проведенная из вершины прямого угла,
разбивает прямоугольный треугольник на два подобных треугольника.
Кроме того, каждый из этих треугольников подобен исходному.
отрезок CD-высота ∆АВС(∟АСВ=90°)
∆АВС
∆АСD
∆CBD
∆АСD
∆АВС
∆CBD
Медиана треугольника делит его на
два равновеликих треугольника.
Медиана п/у треугольника,
проведенная к гипотенузе,
равна половине гипотенузы
А
М
С
В
СМ=1/2 АВ
30.
ba
h
c
c² = a² + b²
31.
В12 см
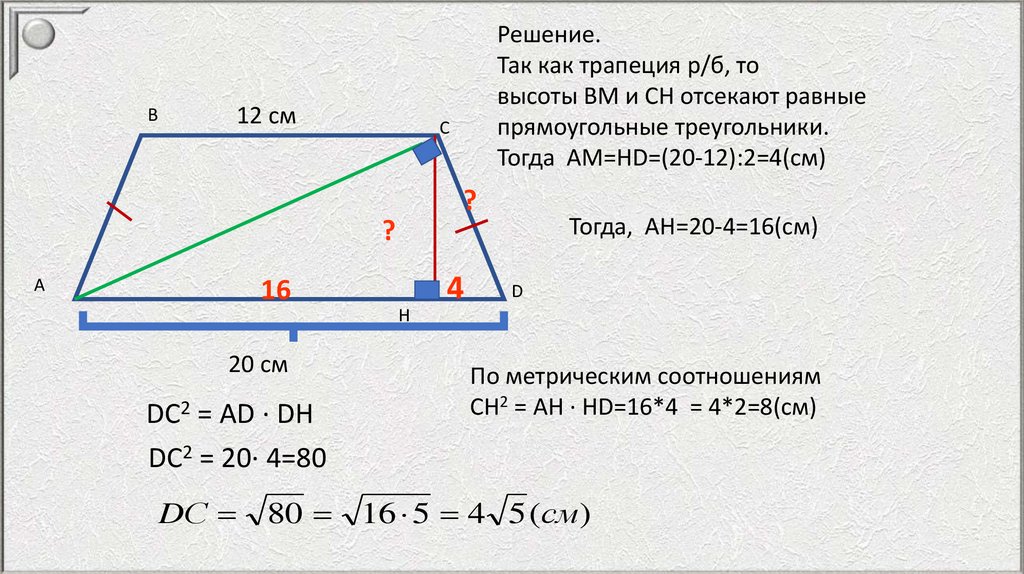
Решение.
Так как трапеция р/б, то
высоты ВМ и СН отсекают равные
прямоугольные треугольники.
Тогда АМ=НD=(20-12):2=4(см)
С
?
Тогда, АН=20-4=16(см)
?
А
16
Н
20 см
DС2 = АD · DН
DC2 = 20· 4=80
DС
4
D
По метрическим соотношениям
СН2 = АН · НD=16*4 = 4*2=8(см)
80 16 5 4 5 (см)
32.
«Я не учу мудрости, я исцеляю от невежества.»ПИФАГОРОВЫ ЗАКОНЫ
• Сыщи себе верного друга; имея его, ты
можешь обойтись без богов.
• Делай лишь то, что впоследствии не
омрачит тебя и не заставит раскаиваться.
• Не пренебрегай здоровьем своего тела.
• Научись жить просто и без роскоши.
• Либо молчи, либо говори то, что ценнее
молчания.
Пифагор Самосский
570 - 480 гг. до н. э
древнегреческий
философ и математик,
создатель религиознофилософской школы
пифагорейцев
33.
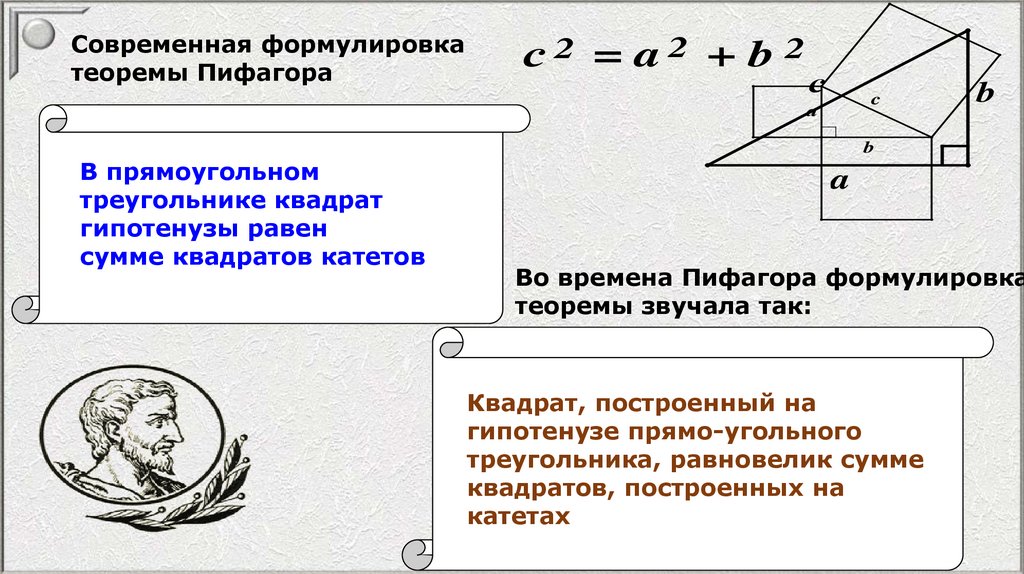
Современная формулировкатеоремы Пифагора
с2 = a2 + b 2
с
c
а
b
b
В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов
a
Во времена Пифагора формулировка
теоремы звучала так:
Квадрат, построенный на
гипотенузе прямо-угольного
треугольника, равновелик сумме
квадратов, построенных на
катетах
34.
Задача №1. Для крепления мачты нужно установить 4 троса. Одинконец каждого троса должен крепиться на высоте 12 м, другой на
земле на расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления мачты?
Задача №2: Египтяне придумали задачу о лотосе:
«На глубине 12 футов растет лотос с 13 футовым
стеблем. Определите, на какое расстояние цветок
может отклониться от вертикали, проходящей
через точку крепления стебля ко дну».
Задача № 3. Пожарные увидели на крыше горящего
дома маленького котенка. Котенок жалобно пищал и
звал на помощь. Но вот беда: пожарная машина не
может приблизится к дому ближе, чем на 6м, высота
дома – 8м. Свою лестницу пожарники могут растянуть
не более, чем на 11м. Достаточно ли этого, чтобы
помочь бедному котенку?
35.
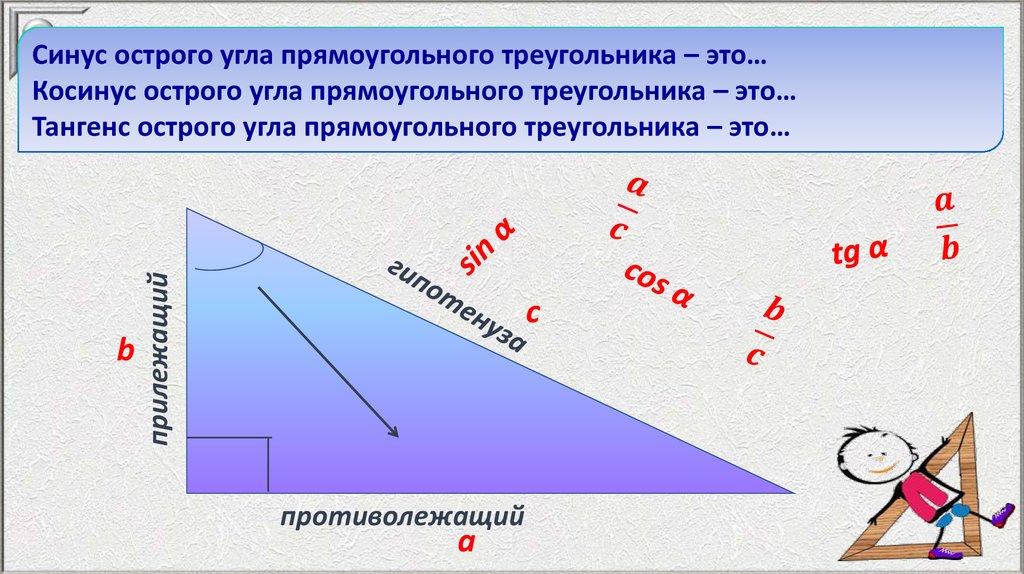
bприлежащий
Синус острого угла прямоугольного треугольника – это…
Косинус острого угла прямоугольного треугольника – это…
Тангенс острого угла прямоугольного треугольника – это…
с
противолежащий
а
36.
Найдите неизвестную сторону треугольников3)
1)
9
2)
5
45ᵒ
60ᵒ
x
60ᵒ
x
1
x
2
3
7
37.
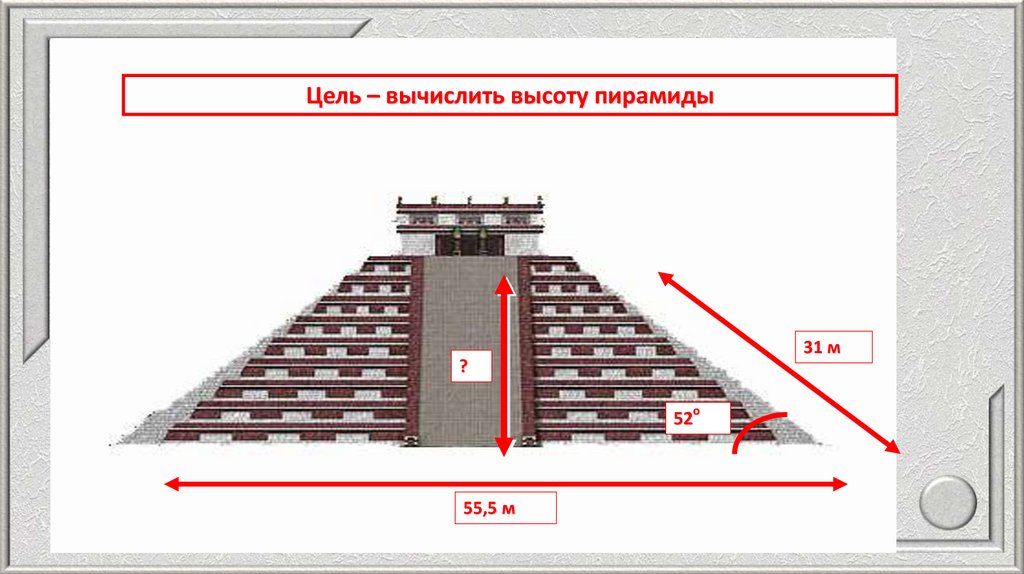
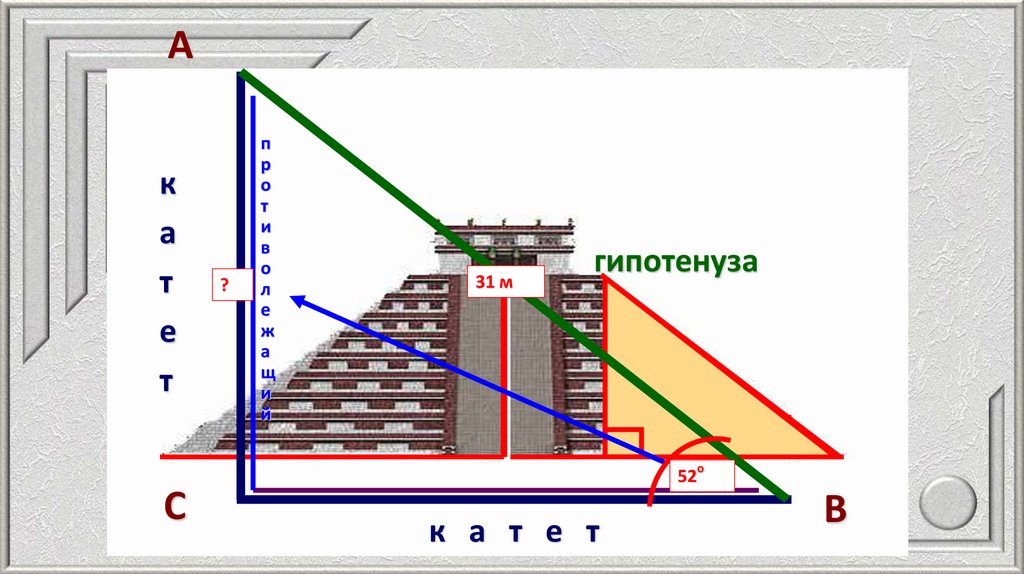
Цель – вычислить высоту пирамиды31 м
?
52о
55,5 м
38.
Ак
а
т
е
т
?
п
р
о
т
и
в
о
л
е
ж
а
щ
и
й
31 м
гипотенуза
52о
С
к а т е т
В
39.
sin В=
AC =
AC
AB
AB
sin 52o 0,79
sin 52o 32 • 0,79
25 м
= 25,28
А
32
?
о
52
С
В
40.
1S ah
2
S mh
S=½ ab
а и b-катеты
если m — средняя линия
h — высота, формула
1
S ab sin
2
площадь
прямоугольного тр-ка
S = p·r
p- полупериметр треугольника
S
p ( p a )( p b)( p c)
Формула Герона
a,b,c – стороны тр-ка
Р – полупериметр тр-ка
r- радиус вписанной окружности
41.
1S ab sin
2
2. Площадь треугольника равна 54, а его периметр 36.
Найдите радиус вписанной окружности.
S = p·r
1
S ah
2
42.
43.
• Многоугольники• Параллелограмм. Свойства и признаки
параллелограмма.
• Прямоугольник
• Ромб
• Квадрат
• Трапеция
44.
Объединение замкнутой ломаной и ее внутренней области называютмногоугольником.
Саму ломаную называют границей многоугольника,
а ее внутреннюю область - внутренней областью
многоугольника.
Отрезок, соединяющий две любые несоседние вершины
многоугольника, называется диагональю.
Количество треугольников
(n-2)
Сумма углов одного треугольника 180
Сумма углов выпуклого n-угольника равна
(n-2)·180
45.
Вариант 1Вариант 2
2. Найти сумму углов выпуклого 12-ка
2. Найти сумму углов выпуклого 8-ка
3. Сколько сторон имеет выпуклый многоугольник,
если сумма его углов равна 1980°?
3. Сколько сторон имеет выпуклый многоугольник,
если сумма его углов равна 2160°?
4. Существует ли выпуклый многоугольник, у
которого все углы равны по 108ᵒ? Если существует,
то найдите число углов.
4. Существует ли выпуклый многоугольник, у
которого все углы равны по 135ᵒ? Если существует,
то найдите число углов.
5. В выпуклом шестиугольнике три стороны равны,
четвертая в два раза больше первой стороны,
пятая - на 3 см меньше четвертой, а шестая – на 1
см больше второй. Найдите стороны
шестиугольника, если известно, что его периметр
равен 30 см.
5. В выпуклом пятиугольнике две стороны равны,
третья сторона на 3 см больше, а четвертая в 2
раза больше первой стороны, пятая – на 4 см
меньше четвертой. Найдите стороны
пятиугольника, если известно, что его периметр
равен 34 см.
46.
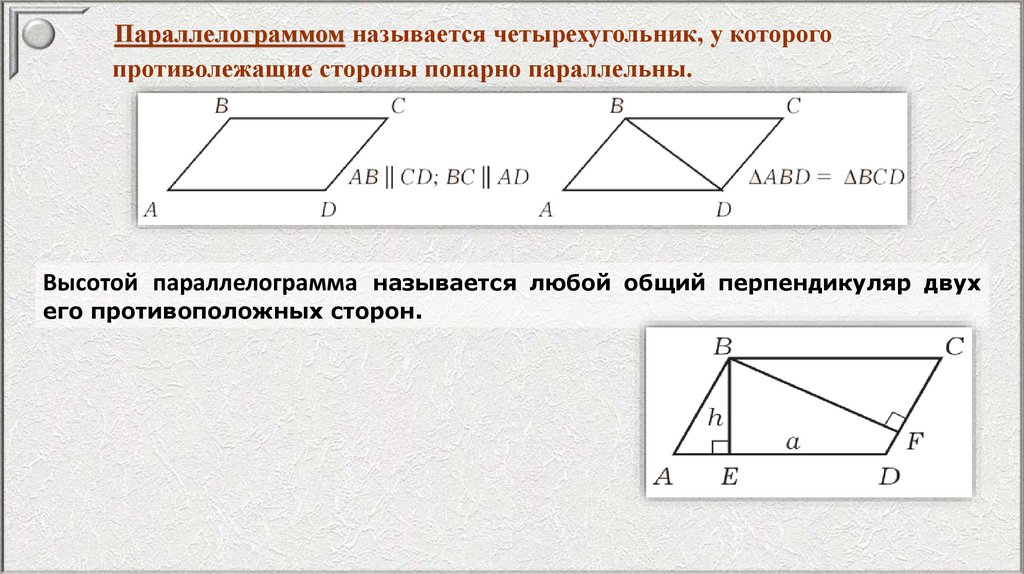
Параллелограммом называется четырехугольник, у которогопротиволежащие стороны попарно параллельны.
Высотой параллелограмма называется любой общий перпендикуляр двух
его противоположных сторон.
47.
Свойства параллелограммаиспользуем, если известно, что
четырехугольник-параллелограмм.
Признаки параллелограмма используем,
если доказываем, что четырехугольник –
параллелограмм.
У параллелограмма:
Четырехугольник-параллелограмм, если:
1.Противолежащие стороны равны;
1.Противолежащие стороны равны;
2. Противолежащие углы равны;
2.Противолежащие углы равны;
3. Диагонали пересекаются и точкой
3.Диагонали пересекаются и точкой
пересечения делятся пополам.
пересечения делятся пополам;
4.Противолежащая пара сторон
одновременно параллельна и равна друг
другу.
48.
Дано: ABCD – парал-м,BE- бис-са <CBA,
AE – бис-са <BAD.
Доказать: BE
AE
Доказательство: AE- бис-са
BE – бис-са
<3=<4.
B
C
4
3
E
1
1
<1=<2.
А
2
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°,
поэтому <ABC+<BAD=180°,
т.е. <1+<2+<3+<4 = 180°.
Т.к. <1=<2, <3=<4, то 2·(<1+<3)=180°, <1+<3=90°.
В ABE < AEB =180°-(<1+<3)=90°, т.е. ВЕ АЕ.
D
49.
Дано:АВСD – параллелограмм, РАВСD = 50 см,
∠С = 30°, BH⊥AD, BH = 6,5 см
Найти:
A B - ?, ВC - ?
Решение
В
С
По свойству параллелограмма
∠С = ∠А = 30°.
∆АВН – прямоугольный,
∠ВН А= 90°
∠А = 30°, следовательно:
∟
А
Н
РАВСD = 2(AD + AB)
50 = 2(13 + AD)
25 = 13 + AD
AD = 25 – 13
AD = 12
D
BH
1
AB
2
т. е АВ = 2· ВН = 2 · 6,5 = 13 (см)
AD = ВС = 12 см
Ответ:
A B = 13см, ВC = 12 см.
50.
Прямоугольником называется параллелограмм, у которого всеуглы прямые.
Т.к. прямоугольник является параллелограммом, то он имеет все свойства
параллелограмма
противоположные стороны и углы равны
диагонали точкой пересечения делятся пополам
все углы прямые
диагонали равны
Диагональ является центром описанной около прямоугольника
окружности.
Диаметр описанной около прямоугольника окружности равен диагонали
прямоугольника
Если один из углов параллелограмма прямой, то этот параллелограмм - прямоугольник
Если диагонали параллелограмма равны, то этот параллелограмм - прямоугольник
51.
52.
Ромб-это параллелограмм, у которого все стороны равныАВ=ВС=СD=АD
D
С
\
Если диагонали параллелограмма
перпендикулярны, то этот
параллелограмм - ромб
\
А
\
Диагонали ромба перпендикулярны
и являются биссектрисами его углов.
В
Если диагональ параллелограмма
является биссектрисой его угла, то
этот параллелограмм - ромб
Прямоугольник с равными сторонами
Параллелограмм у которого диагонали взаимно-перпендикулярны
Параллелограмм, диагональ которого является биссектрисой угла
53.
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:1. Две его смежные стороны равны (отсюда следует, что все стороны равны): АВ =
ВС = СD = AD
2. Его диагонали пересекаются под прямым углом.
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам: ∠BAC =
∠CAD или ∠BDA = ∠BDC
4. Все высоты параллелограмма равны.
5. Диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
54.
Биссектрисы углов А и В параллелограмма АВСD пересекают его стороны ВС и АD в точках F иЕ соответственно. Определите вид четырёхугольника ABEF.
F
В
Доказательство
3
С
1
1 2(нлу; BF AE, АF сек.)
АBF р / б ; АB ВF
3 4 ( нлу; BF AE , BE сек.)
BAE р / б ; BA AE
Т .к. AB BF AE, BF AE, то
AB BF FE EA
А
2
4
E
ABFE пар мм
ABFE ромб
D
55.
• Все стороны равныСвойства квадрата
• Все углы прямые
• Диагонали равны
• Диагонали взаимно перпендикулярны
• Диагонали точкой пересечения делятся пополам
• Диагонали являются биссектрисами углов квадрата
Квадрат – прямоугольник, у которого все стороны равны
56.
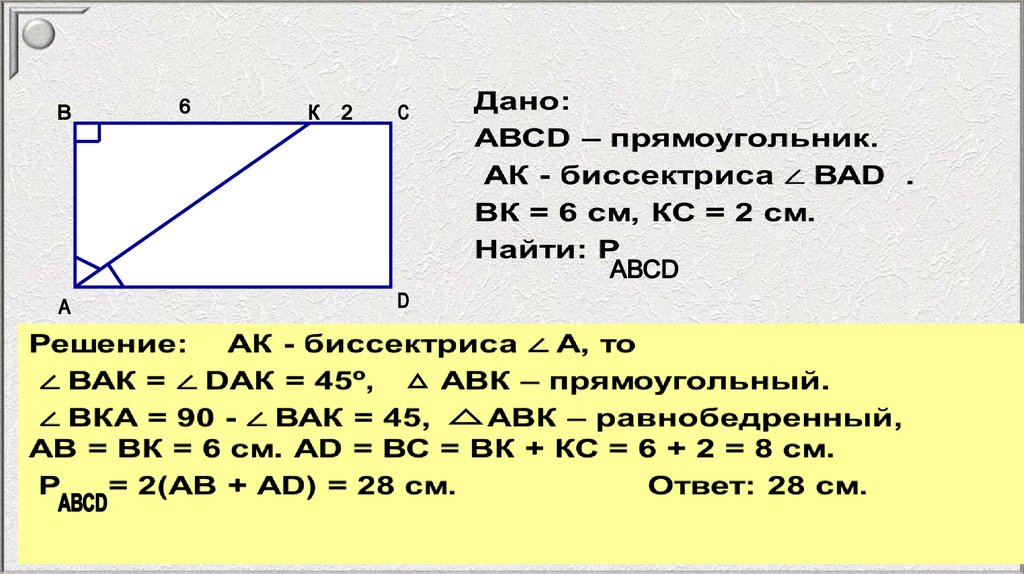
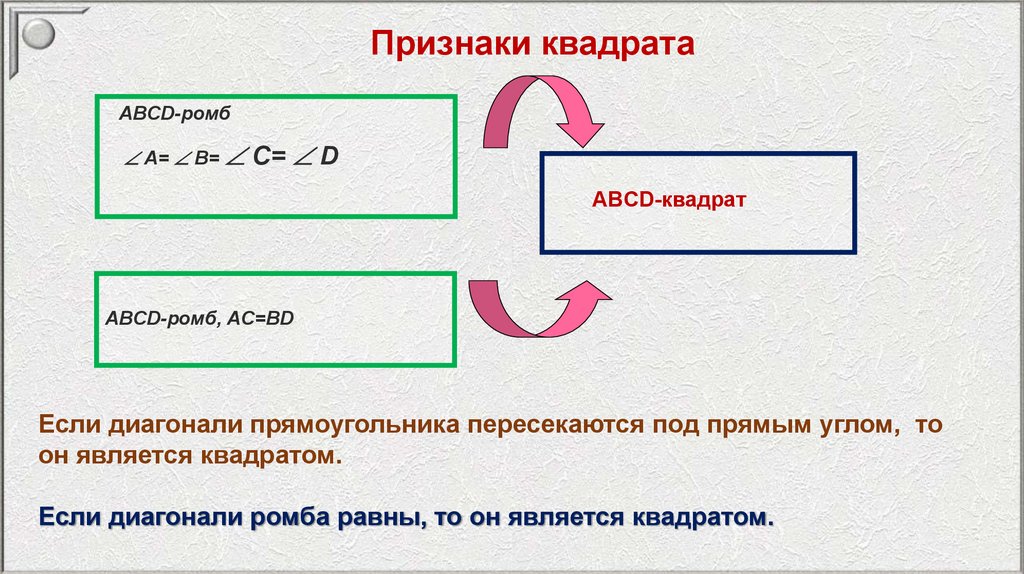
Признаки квадратаABCD-ромб
A= B= C= D
ABCD-квадрат
ABCD-ромб, AC=BD
Если диагонали прямоугольника пересекаются под прямым углом, то
он является квадратом.
Если диагонали ромба равны, то он является квадратом.
57.
от греч. trapeza — стол.Высота р/б трапеции, проведенная из вершины тупого угла, делит
основание трапеции на два отрезка, меньший из которых равен
полуразности оснований, а больший – полусумме оснований
(средней линии трапеции)
Средняя линия трапеции – отрезок, соединяющий середины боковых
сторон.
Средняя линия трапеции параллельна основаниям и равна их
полусумме.
58.
• сумма длин боковых сторон равна сумме длин оснований: AB + CD = BC + AD;• трапеция равнобедренная;
• боковая сторона трапеции видна из центра вписанной окружности под прямым углом.
Треугольники, образованные основаниями и диагоналями,
подобны. Их коэффициент подобия k равен отношению
большего основания к меньшему снованию трапеции.
59.
*Cредняя линия через площадь и высоту:*Высота через площадь и длины оснований:
*Высота через площадь и длину средней линии:
*Площадь через среднюю линию и высоту
S= h·m
*В равнобедренной трапеции длина диагонали равна d =
где с – боковая сторона, a и b – основания
или
d=
*Длина основания через среднюю линию и другое основание
a = 2m - b и b = 2m - a
60.
5B
A
K
C
P
M
61.
№ 28АВСD прямоугольная трапеция.
АВС = 1350
Найти ВС.
В
?
С
450
A
450
30
М
15 15
15
D
62.
1. Диагональ прямоугольника образует угол 51° с одной из его сторон.Найдите острый угол между диагоналями этого прямоугольника.
2. Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=13,
AB =11. Найдите AC.
3. Найдите острый угол угла параллелограмма ABCD, если биссектриса угла A
образует со стороной BC угол, равный 33°.
4. Сумма двух углов равнобедренной трапеции равна 94°. Найдите больший
угол трапеции.
5. В равнобедренной трапеции известна высота, большее основание и угол при
основании (см. рисунок). Найдите меньшее основание.
6.. Сторона ромба равна 38, а один из углов этого
ромба равен 150°. Найдите высоту этого ромба
63.
параллелограммромб
S= ½ d1d2
S= a h
трапеция
квадрат
S=1/2(a+b)h
S=a2
S=1/2d2
прямоугольник
Треугольник
S=ab
S=1/2 ah
64.
1. Найти площадь треугольника ABCB
8
100
50
A
14
C
65.
BC
14
7
30°
A
8,1
D
2. Найти площадь параллелограмма ABCD
H
66.
3. Найти площадь ромба ABCD.B
АС=10
A
C
ВД=16
Д
67.
Дано: ABCD –трапеция, AD AB,C
B
H
A
AB=BC=6см, BCD=135°
Найти: SABCD
Решение
Так как AD AB, то
Проведем CH AD и рассмотрим
DHC
D
DHC=9Oº, DCH= CDH=45º,DH=CH.
Так как CH=AB=6см, то DH=6см,
SABCD=½(AD+BC)·AB
DA=DH+AH=6+6=12(см)
SABCD=½(12+6)·6=54(см²)
68.
69.
• Окружность и круг и их элементы• Свойства окружности
• Взаимное расположение прямой и окружности.
Касательная к окружности
• Описанная и вписанная окружности
треугольника
• Вписанные и описанные четырёхугольники
70.
С окружностью связан ряд полезных теорем и следствий:1. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
2. Отрезки касательных, проведённые из одной точки, равны и составляют равные углы с
прямой, проходящей через эту точку и центр окружности.
3. Вписанный угол измеряется половиной дуги, на которую он опирается( угол, вершина
которого лежит на окружности, а стороны пересекают окружность, называется вписанным).
4. Центральный угол измеряется дугой, на которую он опирается(угол с вершиной в центре
окружности называется центральным).
5. Вписанные углы, опирающиеся на одну дугу равны.
6. Вписанный угол, опирающийся на полуокружность – прямой.
7. Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению
отрезков другой хорды.
8. Квадрат касательной, проведённой к окружности, равен произведению секущей этой
окружности на её внешнюю часть.
9. Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
10. Диаметр окружности, делящий пополам хорду, отличную от диаметра, перпендикулярен этой
хорде.
71.
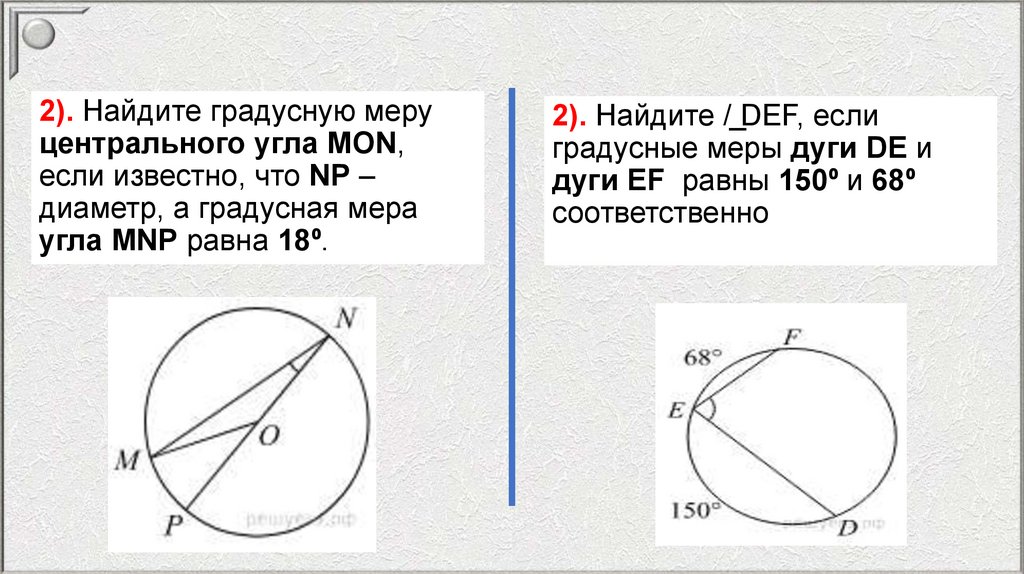
1. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68°соответственно.
2. Прямоугольный треугольник с катетами 5 см и
12 см вписан в окружность. Чему равен радиус
этой окружности?
3. В окружности с центром в точке О проведены
диаметры AD и BC, < OCD = 30°. Найдите величину < OAB.
4. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 70°.
Найдите ∠NMB.
72.
PМ
O
.
Дано : Окружность О.
О1
MN и PK- хорды





























































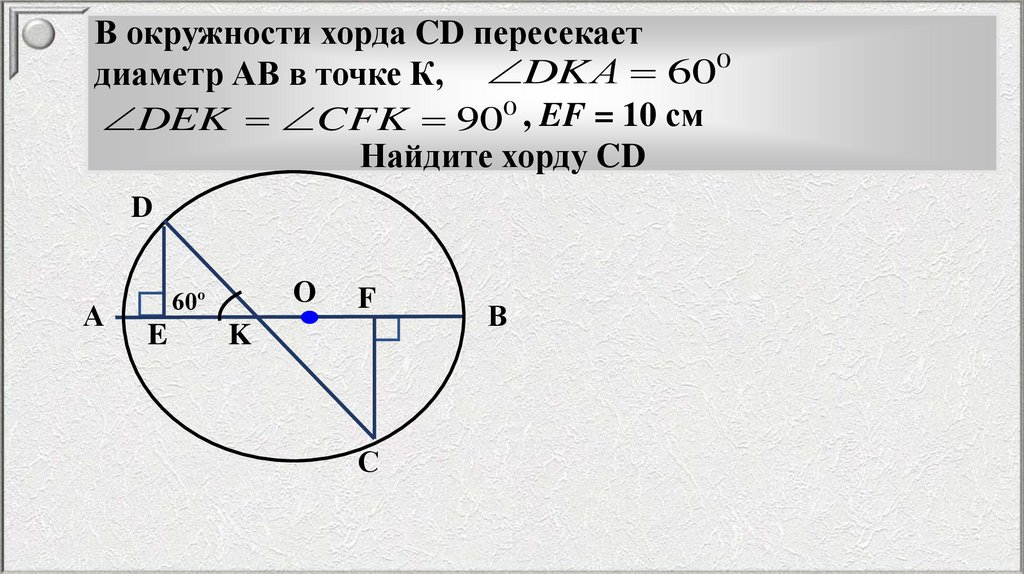












 mathematics
mathematics








