Геометрия, 10 класс

Вставьте пропущенные
слова
Прямоугольный треугольник
Решение прямоугольных треугольников
Теорема _________ : с 2 а 2 b 2
А
b
c
где а – _______, противолежащий α; b - _________, прилежащий к α.
С
a
a
b
h
c
В
Пропорциональные отрезки в прямоугольном треугольнике:
h 2 ca cb ;
b 2 cb c
а 2 са с;
са , сb- __________ ____________на ___________.
Площадь _______________ треугольника:
b
а
S
ab
2
1

4.

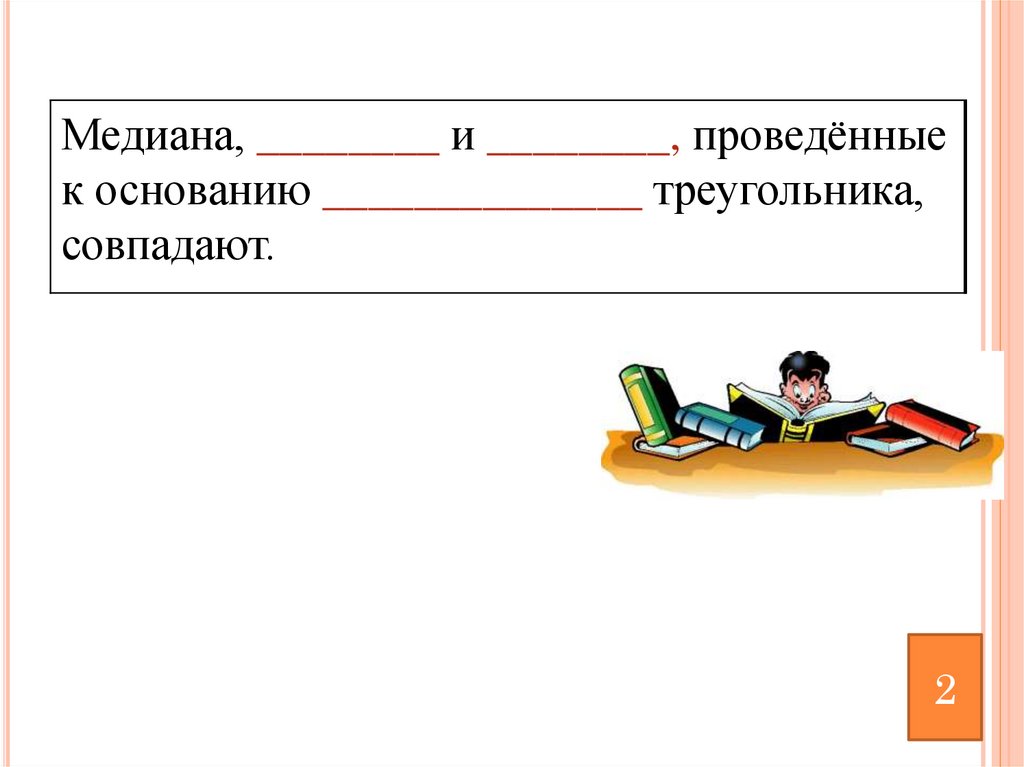
Медиана, ________ и ________, проведённые
к основанию ______________ треугольника,
совпадают.
2

5.

Произвольный треугольник
Площадь треугольника:
с
b
abc
S
;
4___
1
S a b sin ;
2
h
S = ___∙ r;
S p ( p a) ( p b) ( p c) ,
S
1
a h
2
где р – __________
a
А В С ___
Сумма углов в треугольнике:
a
b
c
Теорема ___________:
А
b
c
C
sin A
a
B
R
r
sin B
sin C
2
2
2
с
a
b
2ab sin
Теорема ___________:
R
abc
4S
r
2S
p
3

6.

А
С
В
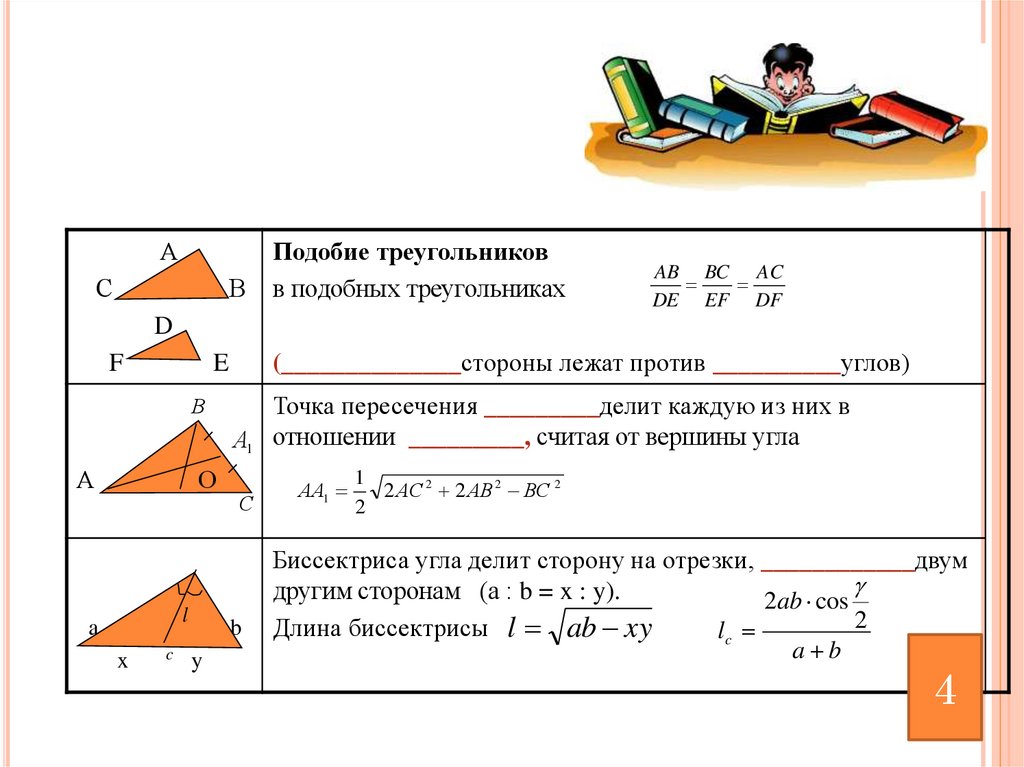
Подобие треугольников
в подобных треугольниках
AB BC AC
DE EF DF
D
F
В
А
О
l
a
x
(______________стороны лежат против __________углов)
E
c
Точка пересечения _________делит каждую из них в
А1 отношении _________, считая от вершины угла
С
b
y
АА1
1
2 АС 2 2 АВ 2 ВС 2
2
Биссектриса угла делит сторону на отрезки, ____________двум
другим сторонам (а : b = x : y).
2ab cos
2
Длина биссектрисы l ab xy
lc
a b
4

7.

Свойства
ABCD – _________________
С AB ___CD, BC ___AD, AB ___CD, BC ___AD,
В
A C , B D
О
A B B C C D A D 1800 ,
φ
α
A
AO ___ OC, BO ___OD,
D
2 ( AB 2 BC 2 ) AC 2 BD 2 .
Признаки
AB //CD, BC //AD ABCD – _____________;
AO = OC, BO = OD ABCD – _____________;
AB = CD, BC = AD ABCD – _____________;
AB = CD, AB ││CD ABCD – _____________;
BC = AD, BC ││AD ABCD – _____________
Площадь:
1
S aha ;
2
S ab sin ;
S
1
d 1 d 2 sin
2
6

8.

Прямоугольник
В
С
О
A
D
Свойства
ABCD – _______________
AB // CD, BC // AD, AB = CD, BC = AD;
А С В D 900 ;
AO = BO = CO = DO
(О – центр _______________окружности, ОА = R).
Признаки
ABCD – параллелограмм, АС = BD ABCD – _______________.
ABCD – параллелограмм, А 90 0
S ab
ABCD – _______________.
_______________
1
S d 2 sin
2
7

9.

Ромб
Свойства
AB//CD, BC//AD, AB = CD = BC = AD;
В
А
О
h
α
С
ABCD – _______________
A B B C C D A D 1800 ,
A C , B D ;
АС ВD , АО = ОС, ВО = ОD;
ВАО DAO, ABO CBO , BCO DCO, ADO CDO
a
D
Признаки
AB = CD= BC = AD ABCD – _______________
ABCD – параллелограмм, АС BD ABCD – ______________
ABCD – параллелограмм, ВАО DAO ABCD – _____________
Площадь
S aha ,
S a 2 sin ,
S
d1 d 2
.
2
8

10.

Квадрат
Свойства
С ABCD –_______________ AB//CD, BC //AD, AB = CD = BC = AD;
А С В D 900 ; АС ВD , AO = BO = CO = DO;
В
а
О
ВАО АВО СВО ВСО DCO CDO ADO DAO 450
d
A
D
Признаки
ABCD – прямоугольник, AB=CD=BC=AD ABCD –______________;
0
ABCD – ромб, А 90 ABCD – квадрат.
Площадь
2
S a
2
d
S
2
9

11.

Произвольная трапеция
B
C
O
φ
A
D
Треугольники AOD и СОВ ____________.
Треугольники АОВ и DOC ____________(их площади равны)
1
____________трапеции: S d1d 2 sin
2
a
m
h
____________трапеции:
b
c
____________линия трапеции:
S
m
a b
2
a b
h m h
2
Вписанная в окружность трапеция – ____________.
В описанной около окружности трапеции:
высота ____________диаметру: h = 2 r;
b
сумма оснований равна сумме ____________ ____________: a + b =
r
d
c+d
a
10

12.

Равнобедренная трапеция
В
С
A
Углы при ____________равны: А D, B C
D
B
C
O
A
D
B
C
h
m
A
H
____________равны: АС = ВD;
отрезки диагоналей равны: АО = DO, BO = CO;
углы, образованные ____________и ____________, равны:
CAD ADB , DBC ACB
Основание ____________, проведённой к большему основанию, делит
основание на отрезки, равные a b и a b
(если ВН – высота, то DH = m,
2
2
где m – _____________ ___________).
D
Если в равнобедренной трапеции диагонали ____________, то высота,
проведённая к основанию, равна _________ _______________:
h = m.
11

13.

Сумма углов многоугольника
В ____________многоугольнике сумма углов равна 1800 (т 2),
где mb – число ____________ (____________) многоугольника.
Свойства правильного многоугольника
О
R
r
A
B
Все стороны ____________, все углы ____________,
О – центр ____________и ____________окружностей,
R – радиус ____________окружности, лежит на биссектрисе угла,
r – радиус ____________окружности, лежит на серединном
перпендикуляре к стороне.
1 3600 : n,
12

14.

Окружность и её элементы
Радиус, проходящий через середину хорды, ____________этой
хорде.
Радиус, перпендикулярный хорде, делит её ____________.
.
.
.
.
Радиус, проведённый в точку касания,
____________касательной.
Отрезки касательных, проведённых из одной точки,
____________.
Центр окружности лежит на ____________угла, образованного
.
____________,
проведёнными из одной точки.
Вписанный угол, опирающийся на диаметр, равен ___________
13

15.

Окружность и её элементы
Градусная мера ____________угла равна градусной мере
____________, на которую он ____________.
m
m
n
Вписанный угол измеряется ____________дуги, на которую он
____________.
n
Вписанные углы, опирающиеся на одну дугу, ____________.
Если две хорды окружности пересекаются, то произведение
отрезков одной хорды равно произведению отрезков другой
хорды.
14

16.

Окружность, вписанная в треугольник
Отрезок, соединяющий центр окружности и точку её
касания со стороной, ____________этой стороне.
Отрезки двух соседних сторон от общей вершины до
точек касания ____________.
Центр вписанной окружности лежит на
____________угла, образованного двумя сторонами.
15

17.

Окружность, описанная около треугольника
Центр ____________окружности лежит на
____________перпендикуляре к любой из сторон
треугольника.
Если прямоугольный треугольник вписан в
окружность, то его гипотенуза является
____________окружности.
Угол вписанного в окружность треугольника в 2 раза
меньше центрального угла, опирающегося на ту же
дугу, и равен любому другому вписанному углу,
опирающемуся на ту же дугу.
16

18.

№1
С 90 0
В треугольнике АВС
,
АВ= 30, АС 3 19 . Найдите sin А.
A
30
3 19
C
B

19.

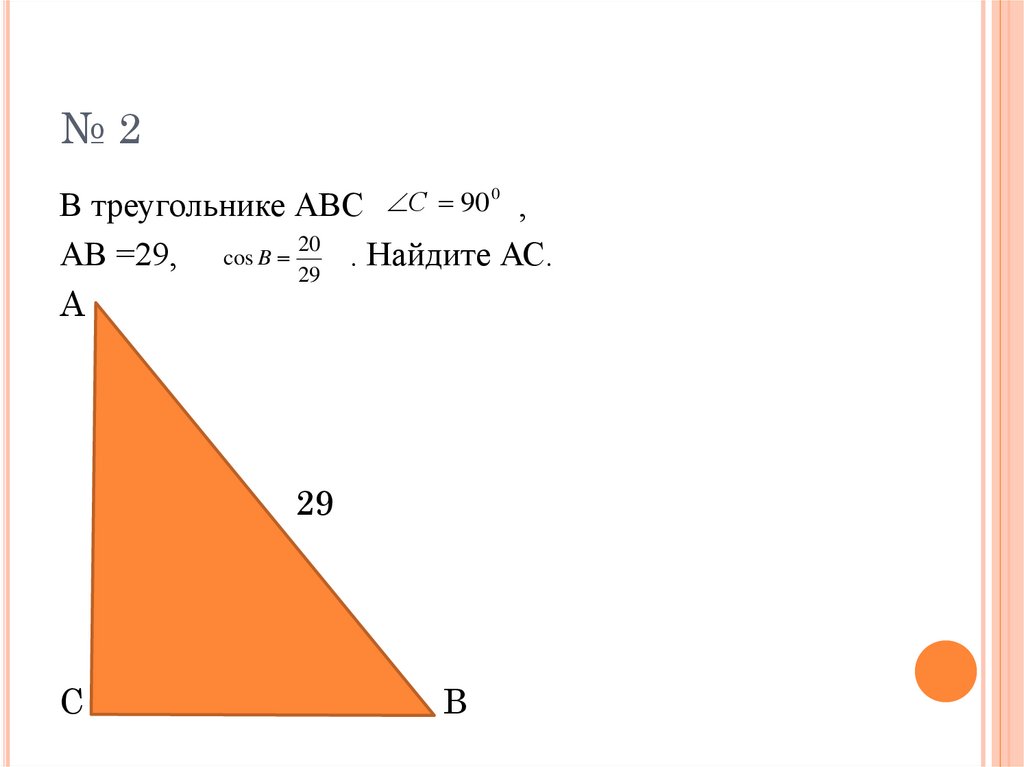
№2
В треугольнике АВС С 90 ,
АВ =29, cos B 20
. Найдите АС.
29
А
0
29
С
В

20.

№3
В равнобедренном треугольнике АВС с основанием
АС боковая сторона АВ = 10, а высота, проведённая к
основанию, равна 2 21 . Найдите косинус угла А.
В
10
2 21
А
С
Н

21.

№4
Найдите площадь треугольника, изображённого на
рисунке.
У
5
2
Х
0
2
У
6

22.

№5
Площадь параллелограмма АВСD равна 16,
диагональ АС равна 2, угол АСD 450
Найдите сторону ВС.
B
A
C
D

23.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Точка О является центром окружности, описанной около
треугольника АВС. Найдите площадь треугольника АОС, если
известно, что ВС = 6, АСВ 150 , САВ 300.
(Ответ: 18)
2. В равнобедренный прямоугольный треугольник с катетом,
равным 1, вписан квадрат, имеющий с треугольником общий
прямой угол. Найдите периметр квадрата.
(Ответ: 2)
3. Основания равнобедренной трапеции равны 51 и 65. Боковые
стороны равны 25. Найдите синус острого угла трапеции.
(Ответ: 0,96)
4. Основания равнобедренной трапеции равны 14 и 26, а ее
периметр равен 60. Найдите площадь трапеции.
(Ответ: 160)

English Русский Rules