Similar presentations:
Вводное повторение. Геометрия. 10 класс
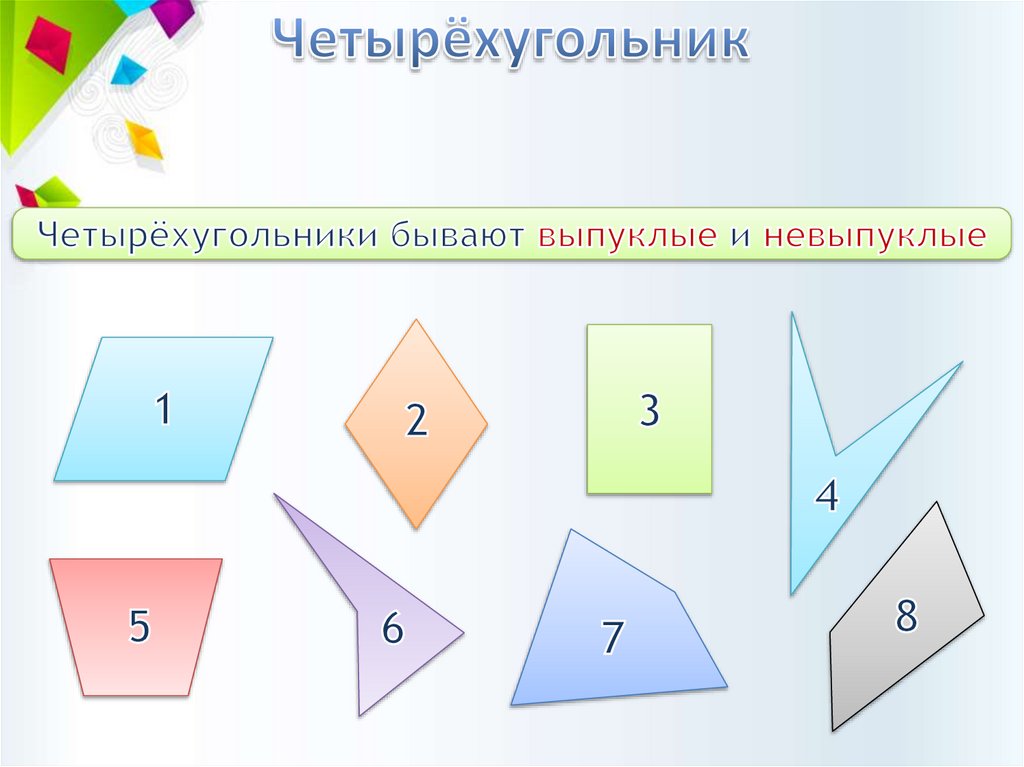
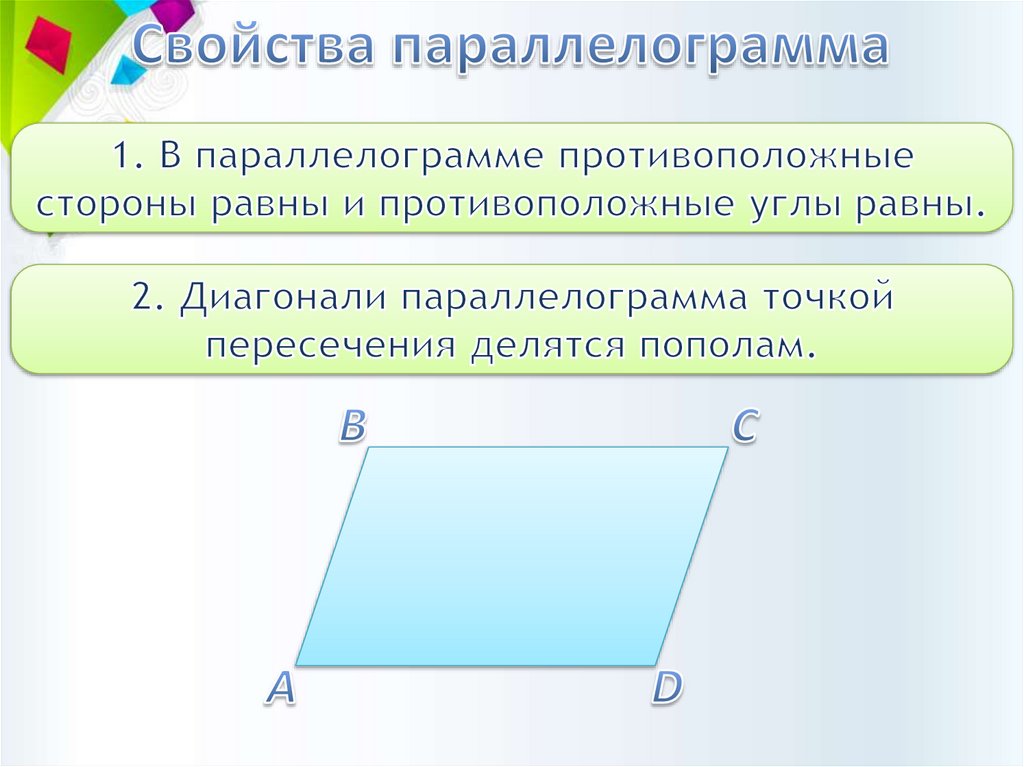
1.
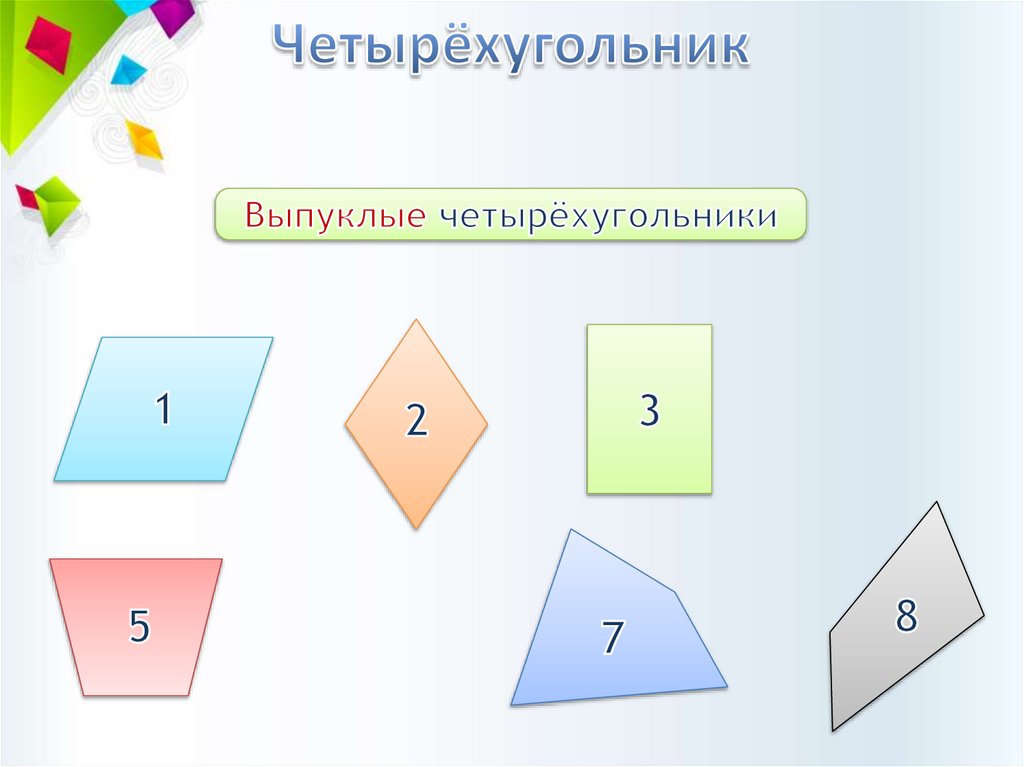
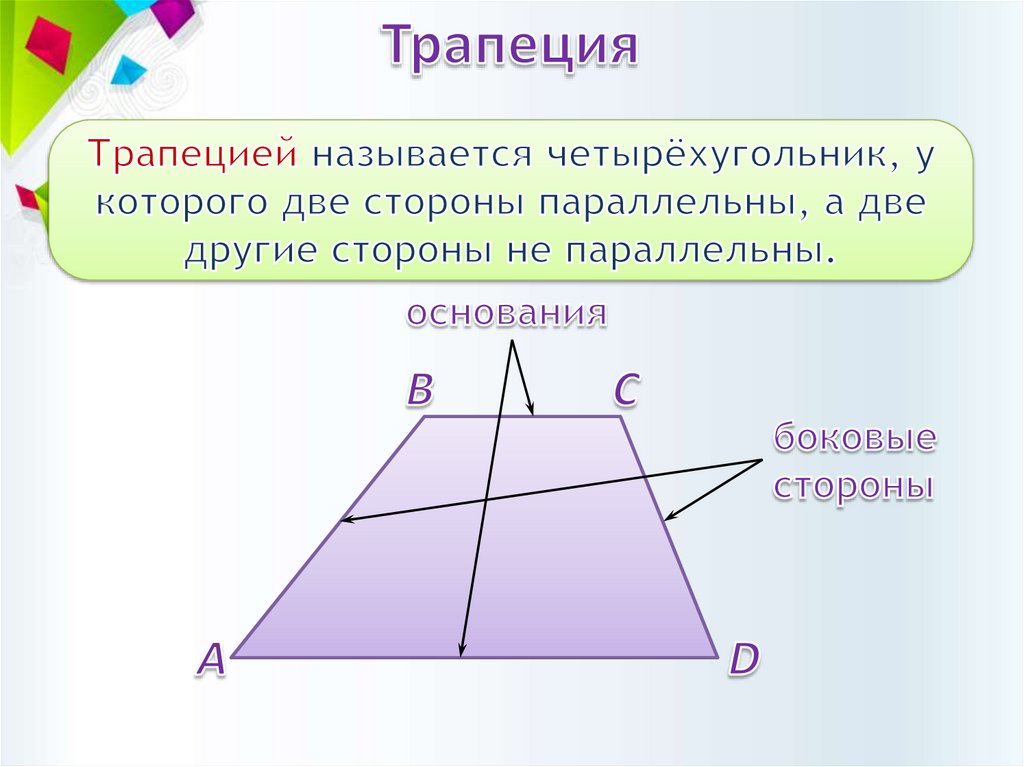
2.
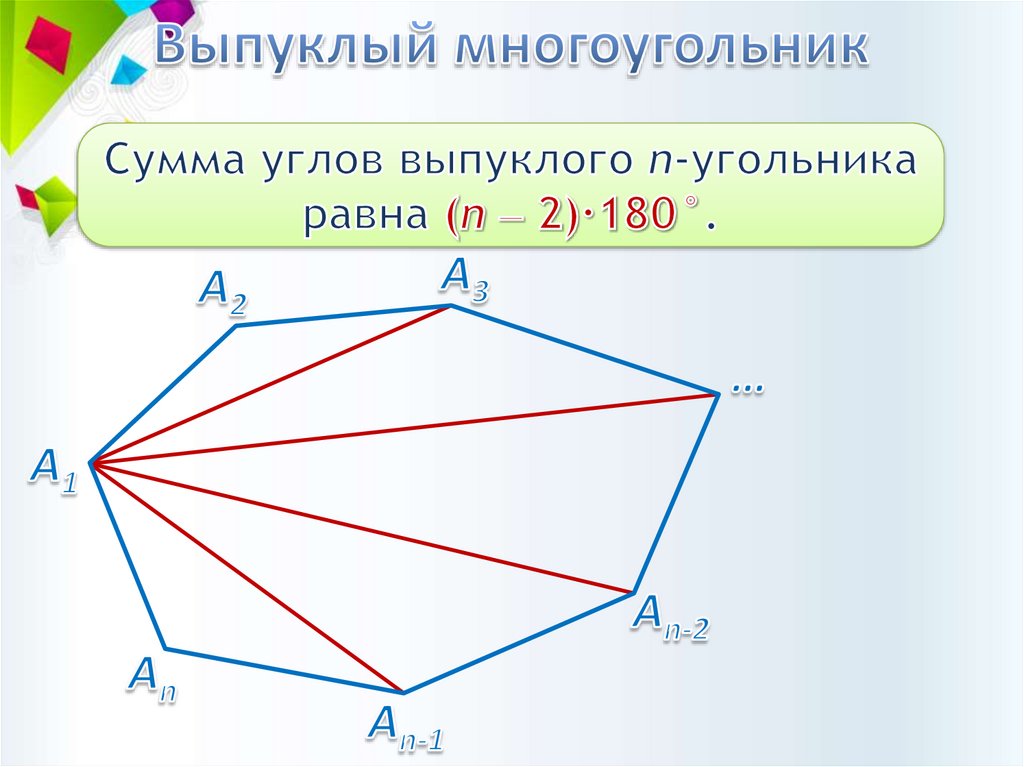
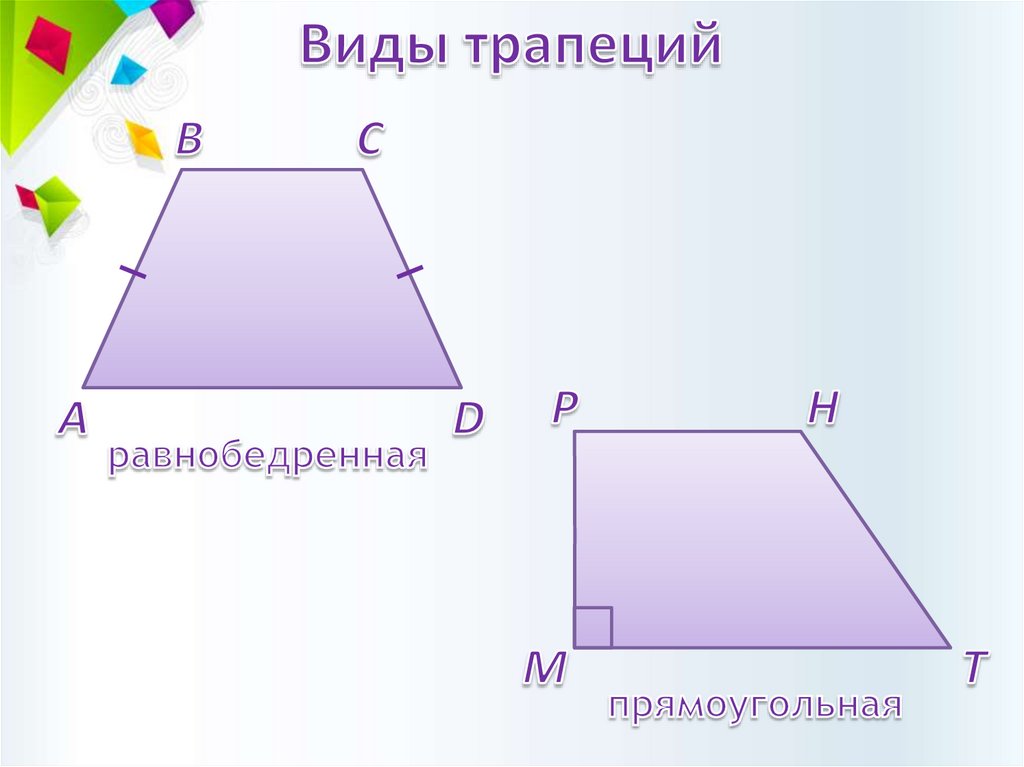
3.
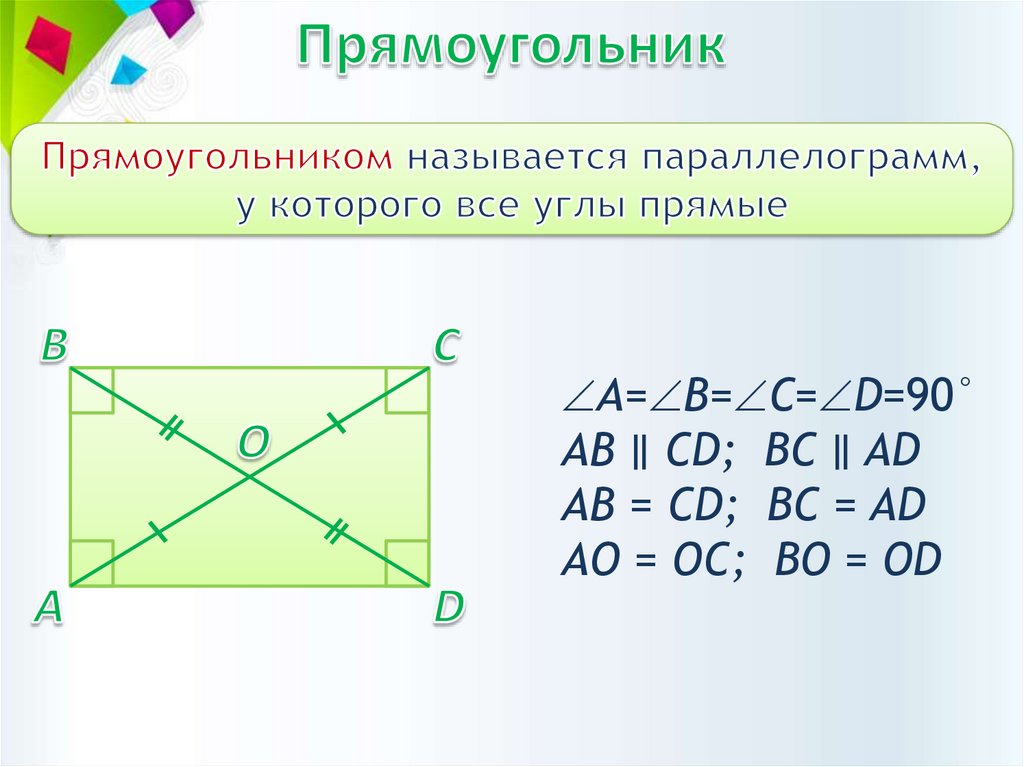
4.
5.
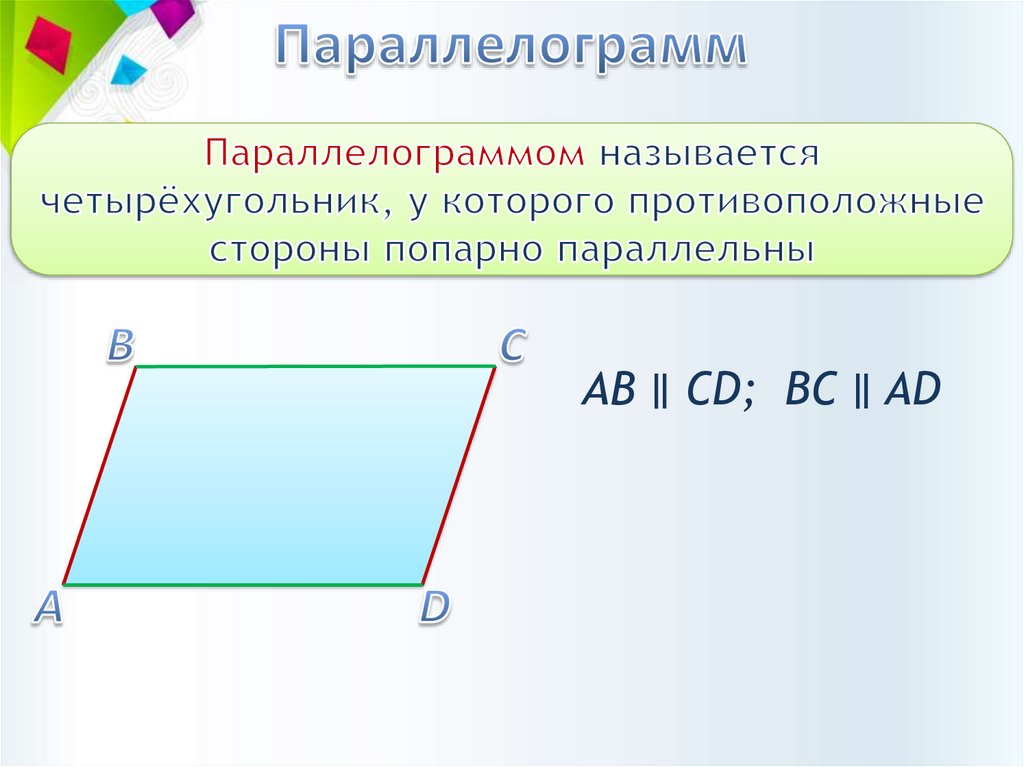
АВ ∥ CD; BC ∥ AD6.
7.
8.
9.
10.
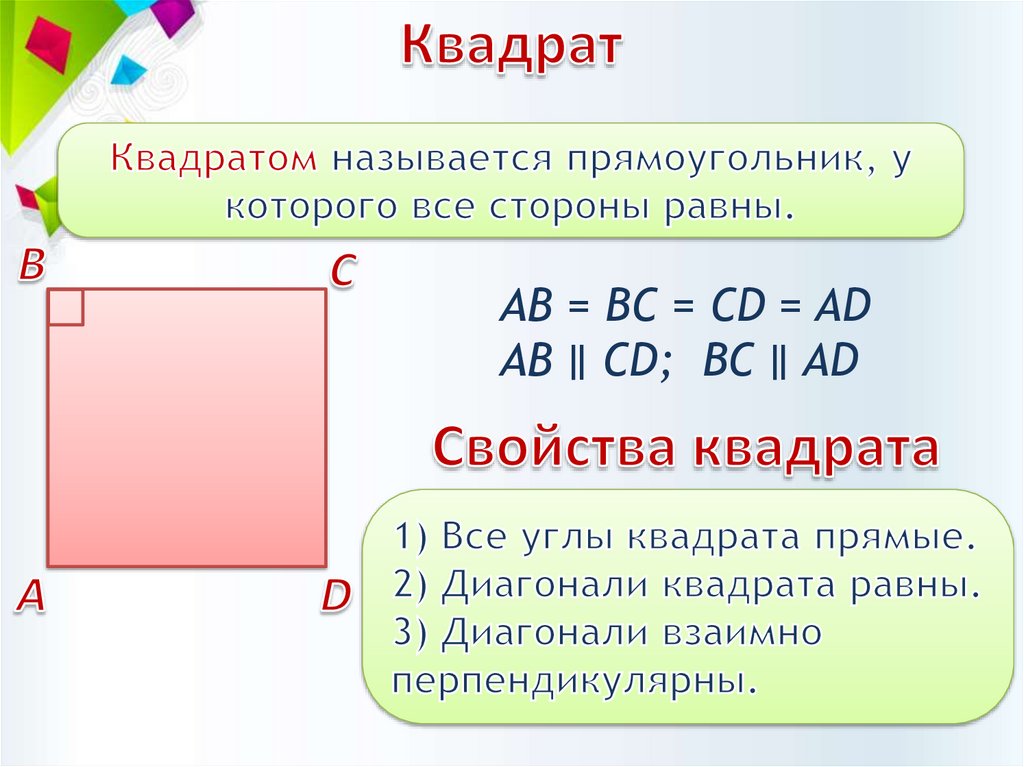
А= В= С= D=90°АВ ∥ CD; BC ∥ AD
АВ = CD; BC = AD
АО = ОC; BО = ОD
11.
12.
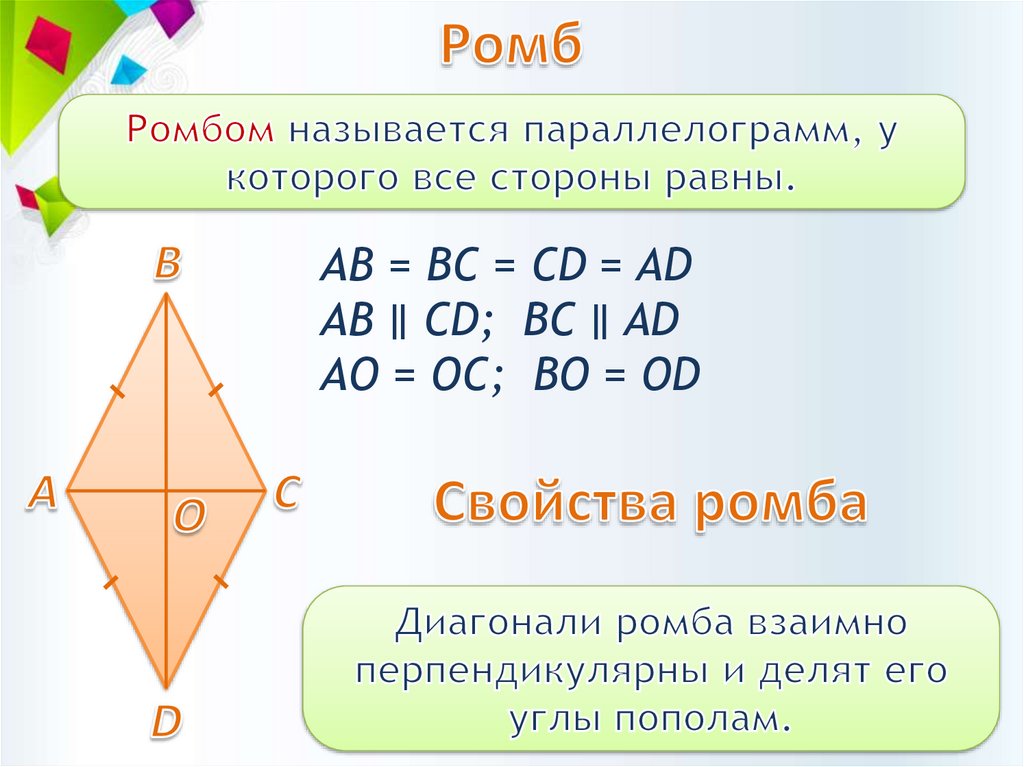
АВ = BC = CD = ADАВ ∥ CD; BC ∥ AD
АО = ОC; BО = ОD
13.
АВ = BC = CD = ADАВ ∥ CD; BC ∥ AD
14.
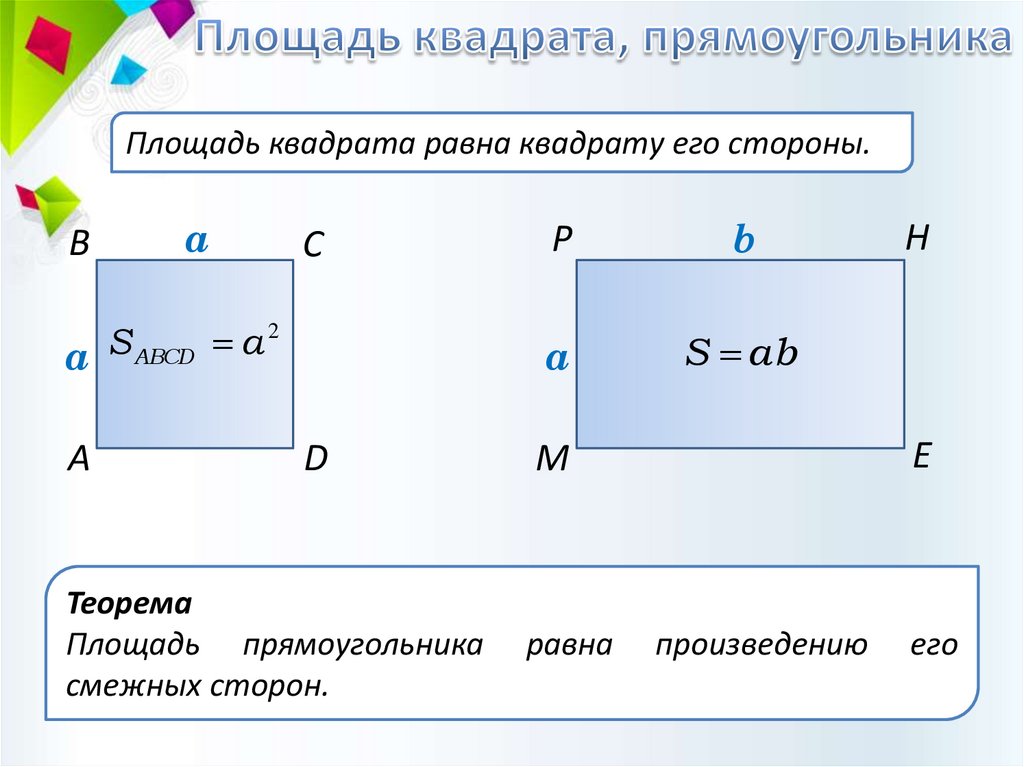
Площадь квадрата равна квадрату его стороны.B
a
C
2
S
a
a ABCD
A
D
Теорема
Площадь прямоугольника
смежных сторон.
Р
b
a
S ab
Е
М
равна
Н
произведению
его
15.
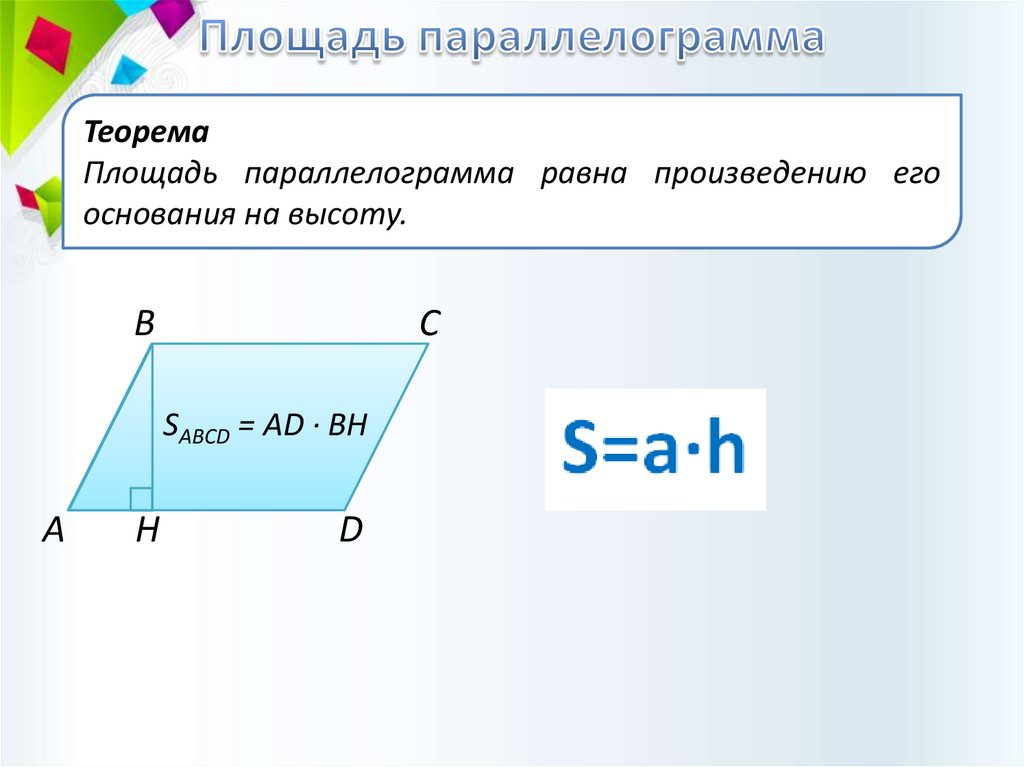
ТеоремаПлощадь параллелограмма равна произведению его
основания на высоту.
B
C
SABCD = AD · BH
A
Н
D
16.
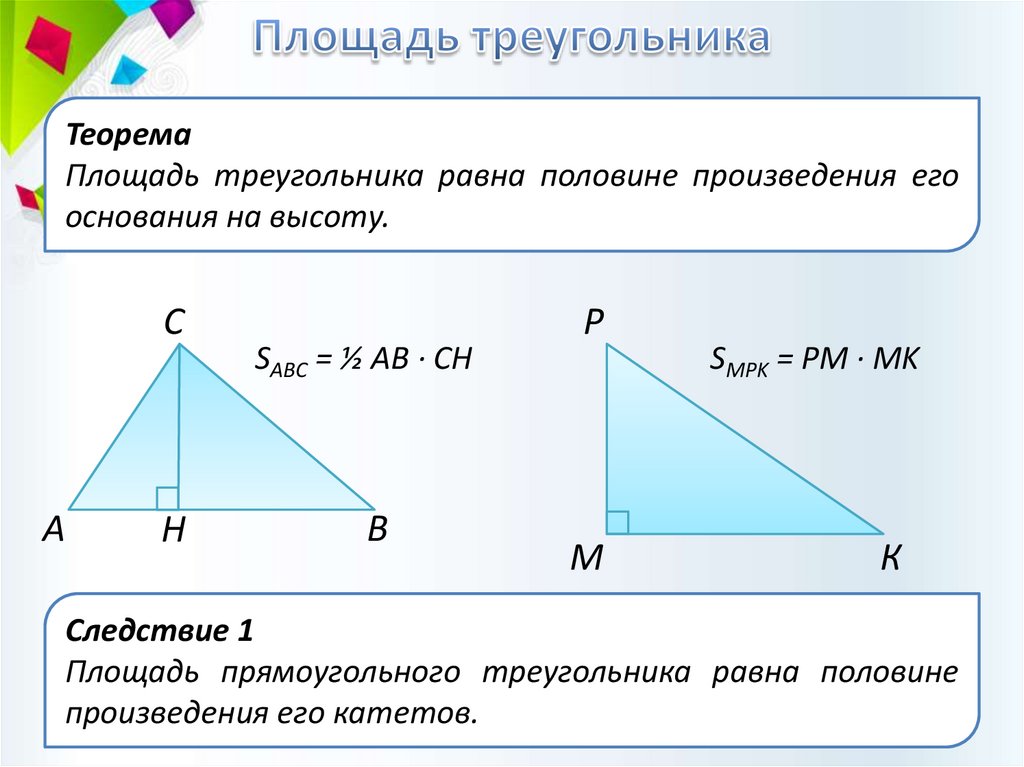
ТеоремаПлощадь треугольника равна половине произведения его
основания на высоту.
C
A
Н
SABC = ½ AB · CH
B
Р
М
SMPK = PM · MK
К
Следствие 1
Площадь прямоугольного треугольника равна половине
произведения его катетов.
17.
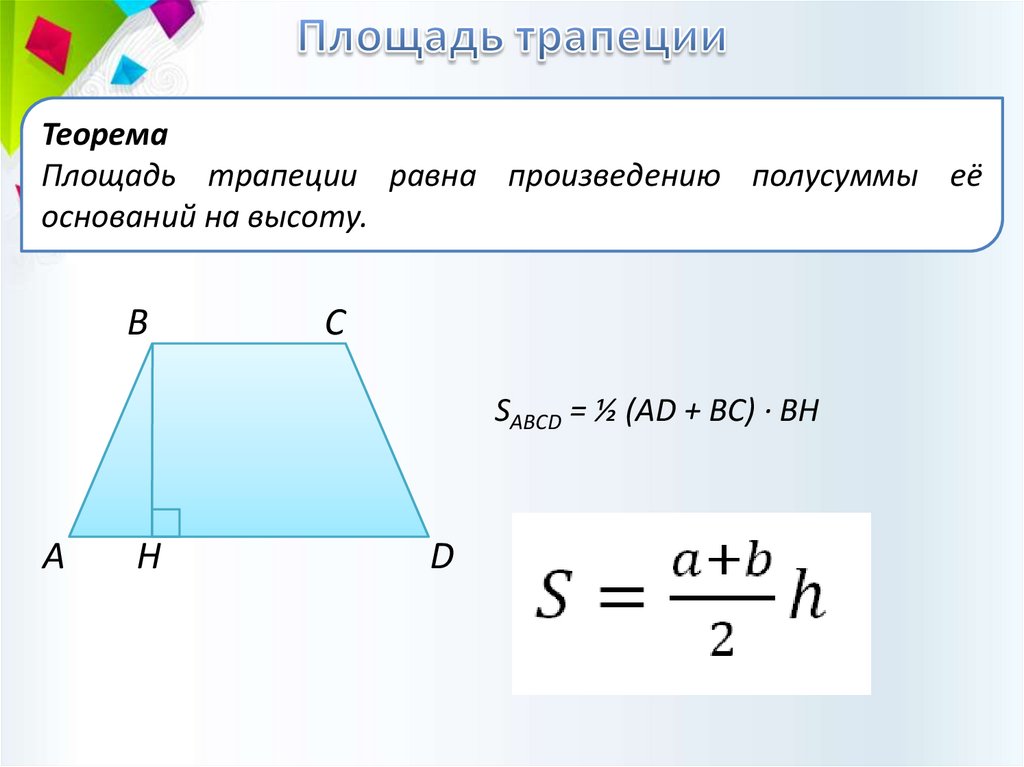
ТеоремаПлощадь трапеции равна произведению полусуммы её
оснований на высоту.
В
С
SABCD = ½ (AD + BC) · BH
A
Н
D
18.
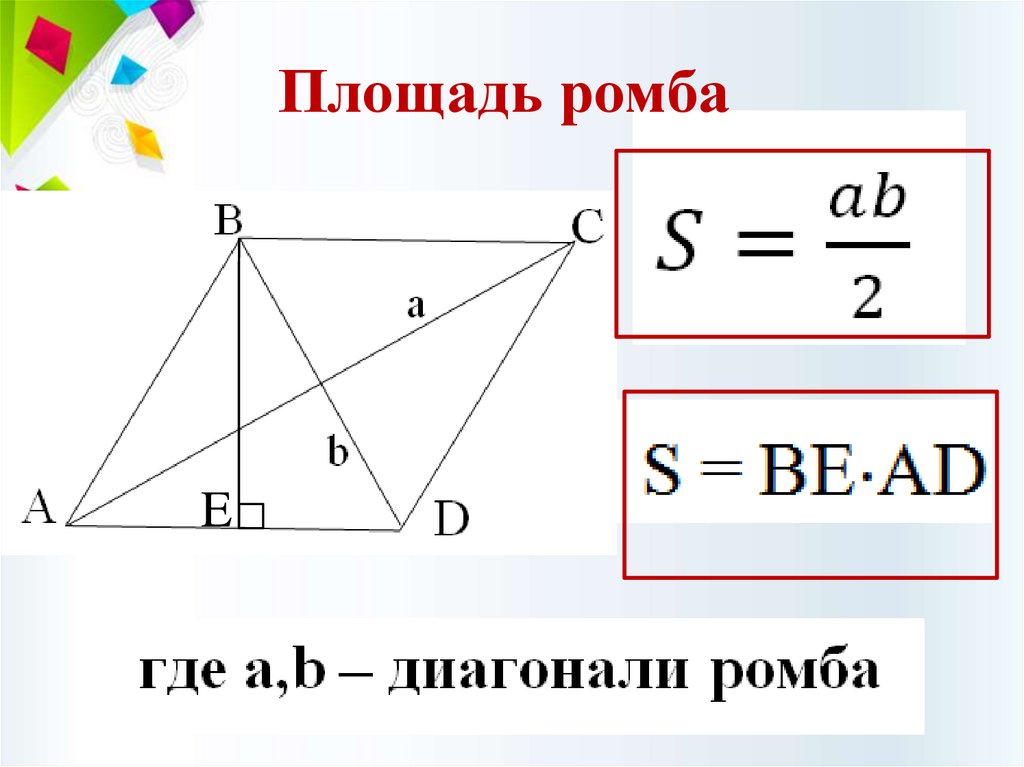
Площадь ромбаE
19.
В прямоугольном треугольнике квадрат гипотенузы равенсумме квадратов катетов.
c
a
b
20.
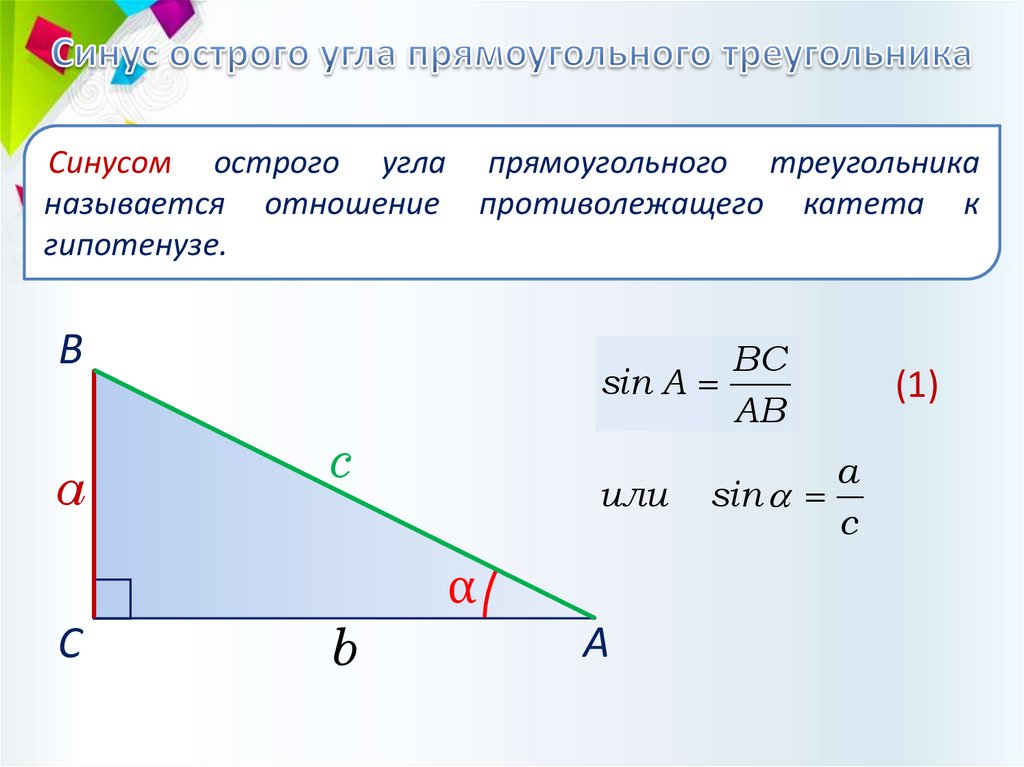
Синусом острого угла прямоугольного треугольниканазывается отношение противолежащего катета к
гипотенузе.
В
a
BC
sin A
AB
c
или
α
С
b
А
a
sin
c
(1)
21.
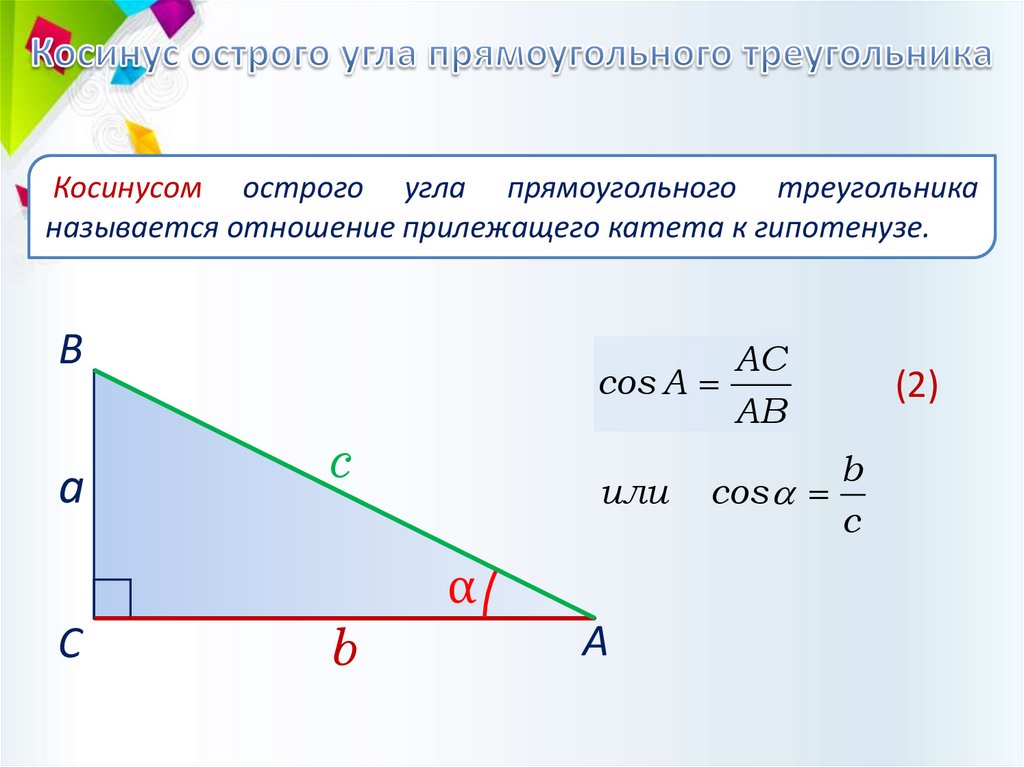
Косинусом острого угла прямоугольного треугольниканазывается отношение прилежащего катета к гипотенузе.
В
a
AC
cos A
AB
c
или
α
С
b
А
b
cos
c
(2)
22.
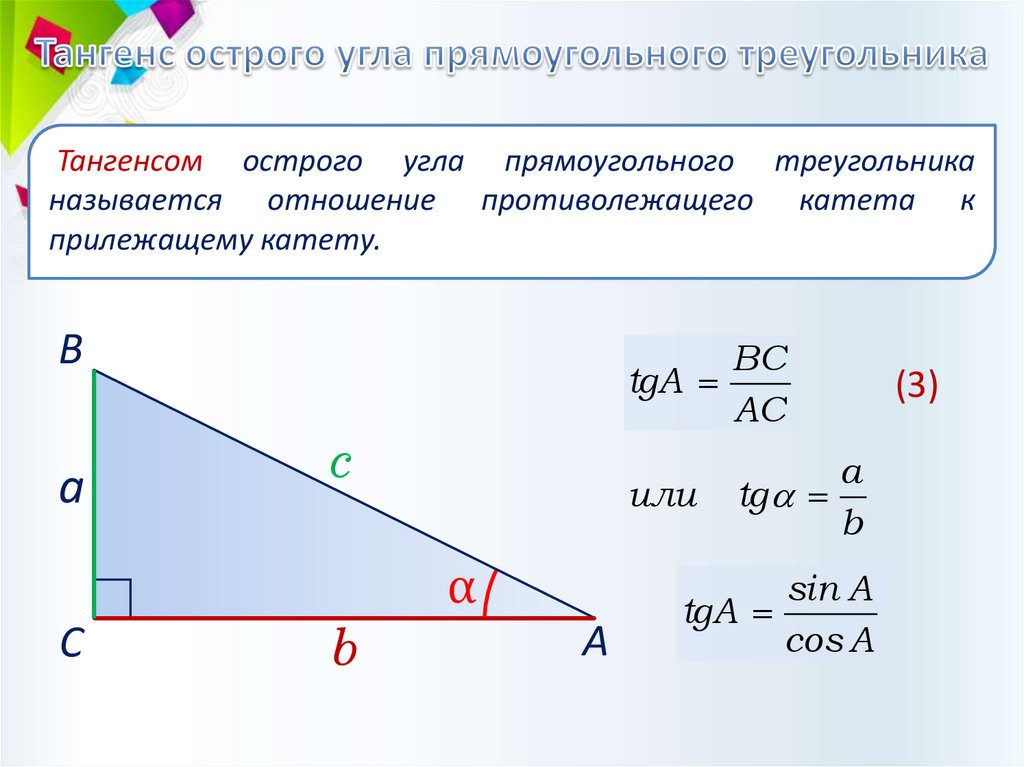
Тангенсом острого угла прямоугольного треугольниканазывается отношение противолежащего катета к
прилежащему катету.
В
a
BC
tgA
AC
c
или
α
С
b
А
a
tg
b
sin A
tgA
cos A
(3)
23.
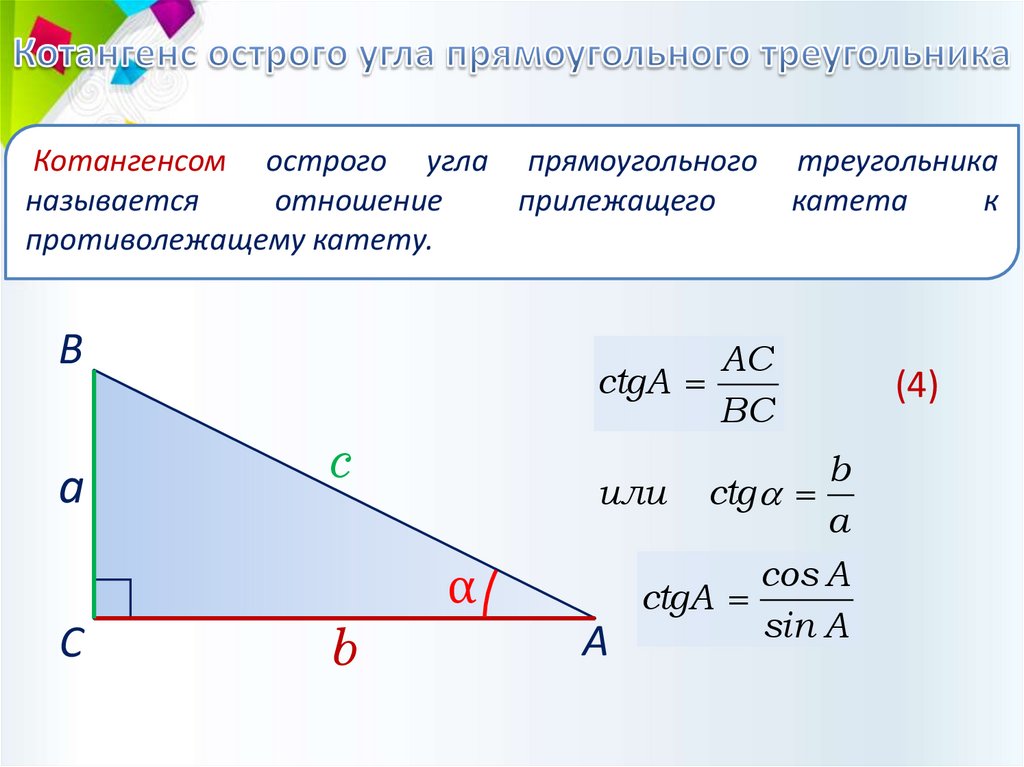
Котангенсом острого угла прямоугольногоназывается
отношение
прилежащего
противолежащему катету.
В
a
АC
сtgA
ВC
c
α
С
b
треугольника
катета
к
b
или сtg
а
cos A
сtgA
sin A
А
(4)
24.
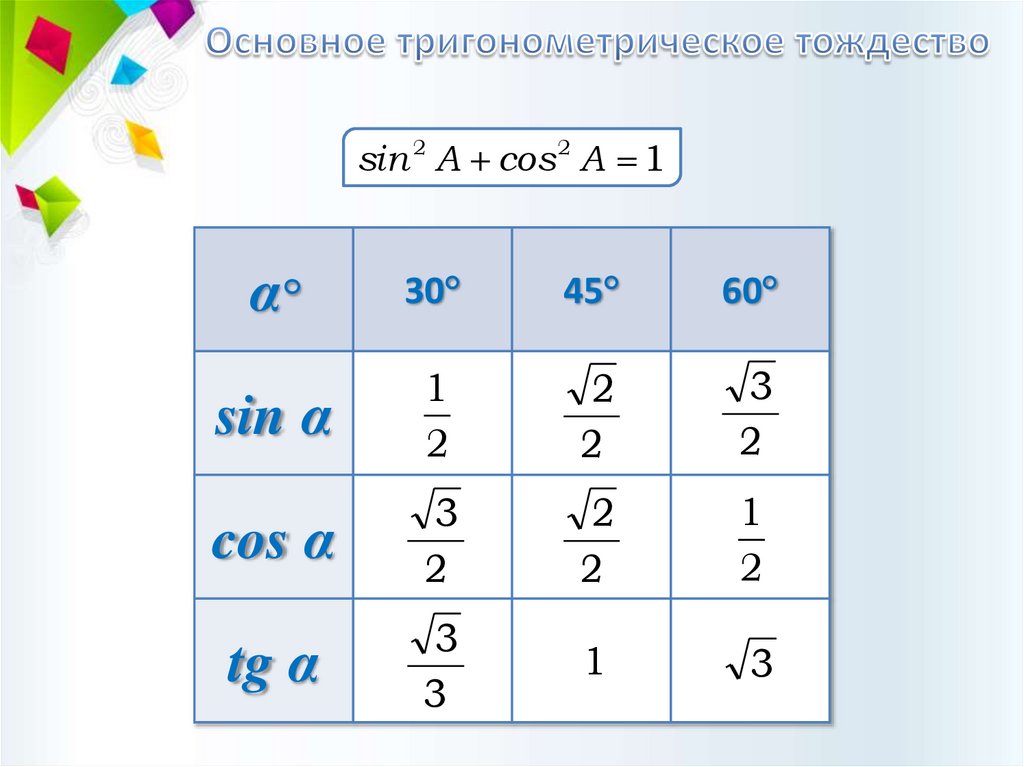
sin 2 A cos 2 A 1α°
30°
45°
60°
sin α
1
2
2
2
3
2
cos α
3
2
2
2
1
2
tg α
3
3
1
3
25.
Если два угла одного треугольника соответственно равныдвум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, заключенные
между этими сторонами, равны, то такие треугольники
подобны.
Если три стороны одного треугольника пропорциональны
трем сторонам другого треугольника, то такие
треугольники подобны.
26.
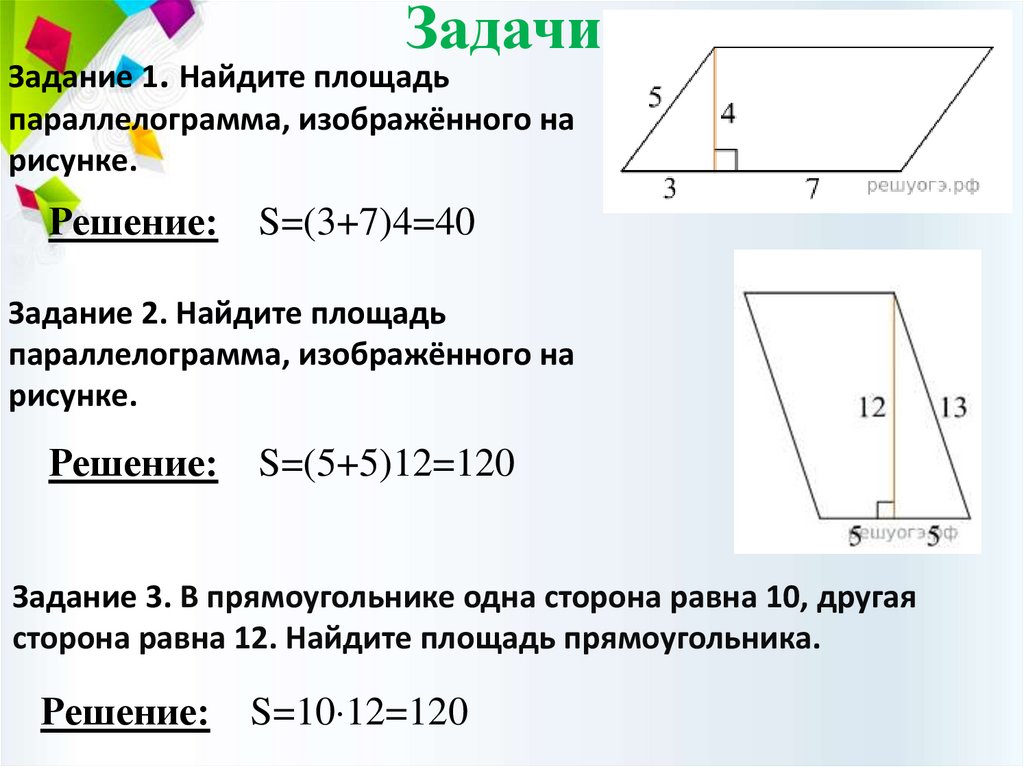
ЗадачиЗадание 1. Найдите площадь
параллелограмма, изображённого на
рисунке.
Решение:
S=(3+7)4=40
Задание 2. Найдите площадь
параллелограмма, изображённого на
рисунке.
Решение:
S=(5+5)12=120
Задание 3. В прямоугольнике одна сторона равна 10, другая
сторона равна 12. Найдите площадь прямоугольника.
Решение:
S=10 12=120
27.
Задание 4. Найдите площадь трапеции,изображённой на рисунке.
Решение:
Задание 5. Площадь ромба равна 27, а периметр равен 36.
Найдите высоту ромба.
Решение:
28.
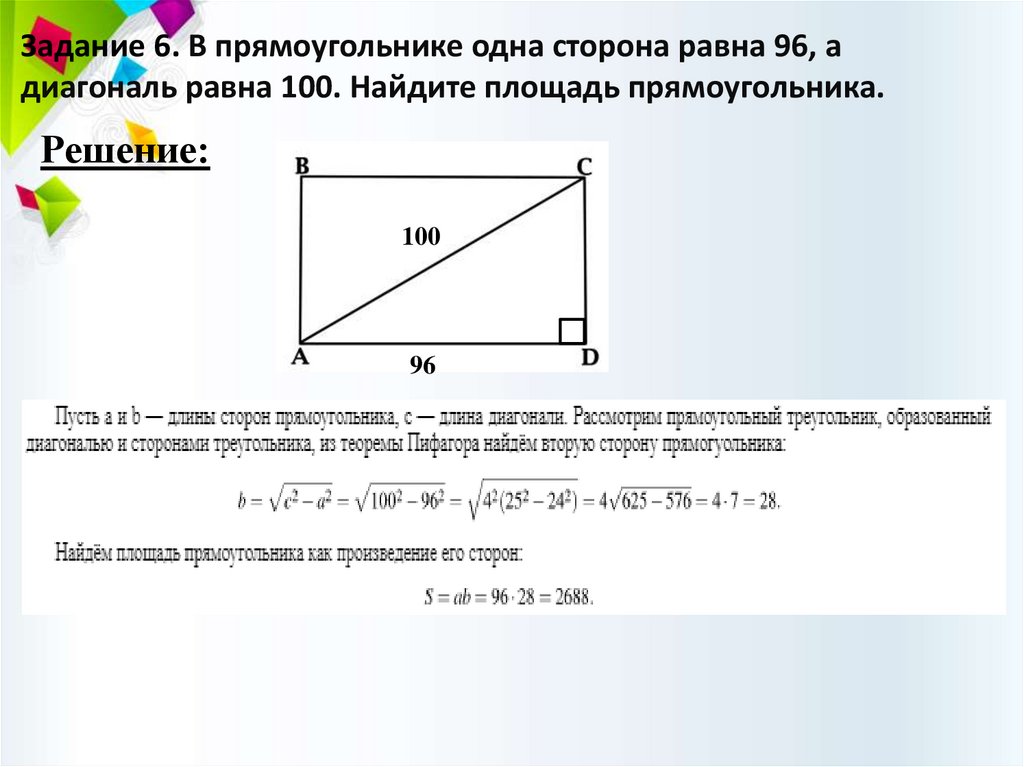
Задание 6. В прямоугольнике одна сторона равна 96, адиагональ равна 100. Найдите площадь прямоугольника.
Решение:
100
96
29.
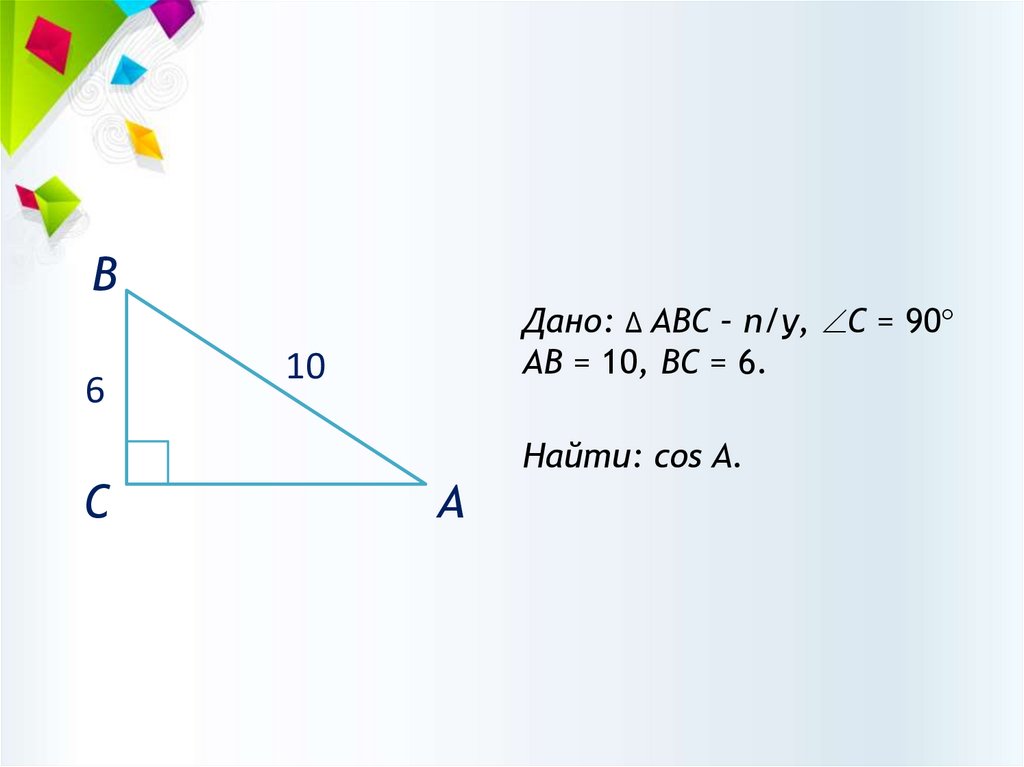
В6
Дано: ∆ АВС – п/у, С = 90
АВ = 10, ВС = 6.
10
Найти: cos A.
С
А
30.
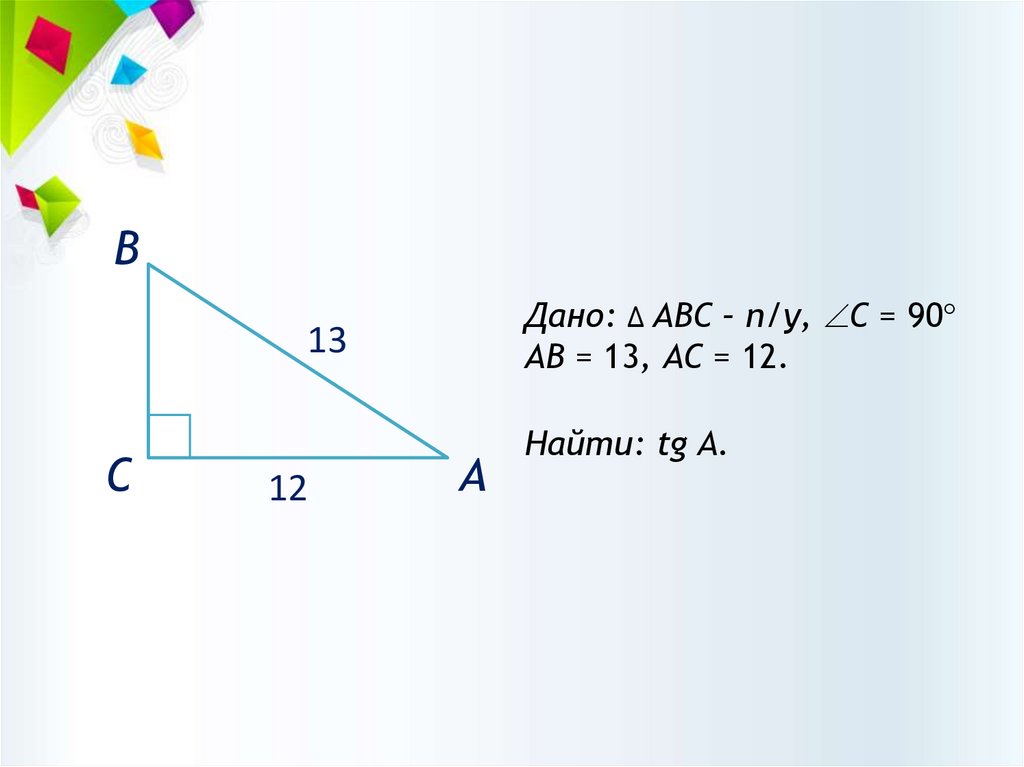
ВДано: ∆ АВС – п/у, С = 90
АВ = 13, АС = 12.
13
С
12
А
Найти: tg A.
31.
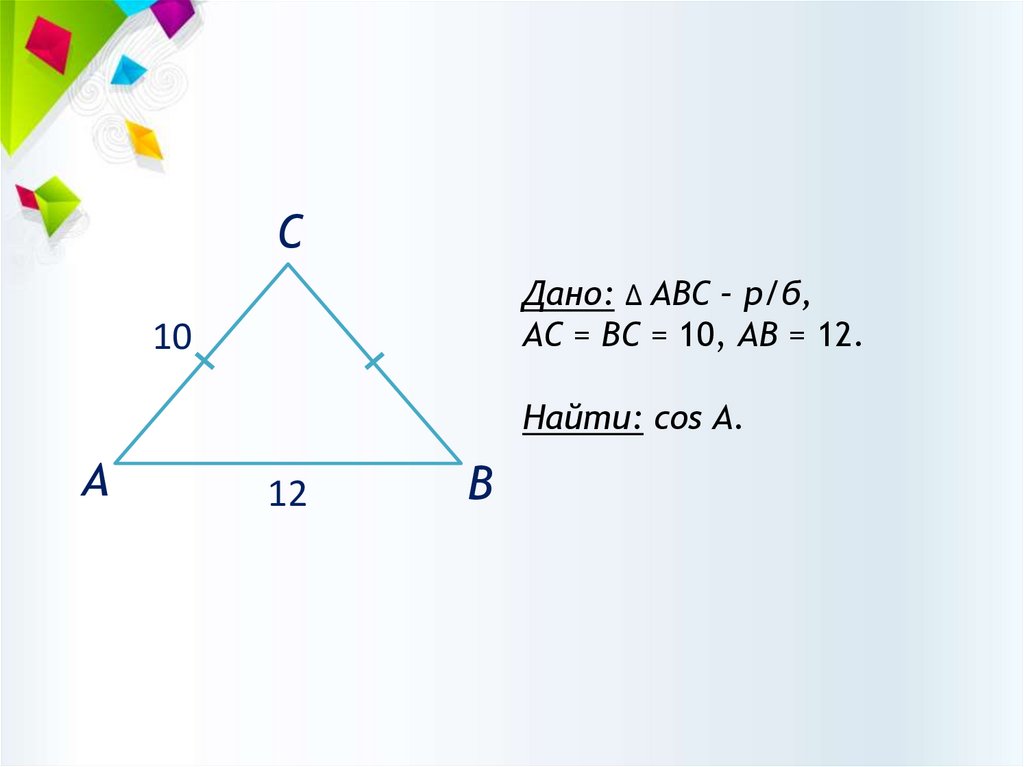
СДано: ∆ АВС – р/б,
АС = ВС = 10, АВ = 12.
10
Найти: cos А.
А
12
В
32.
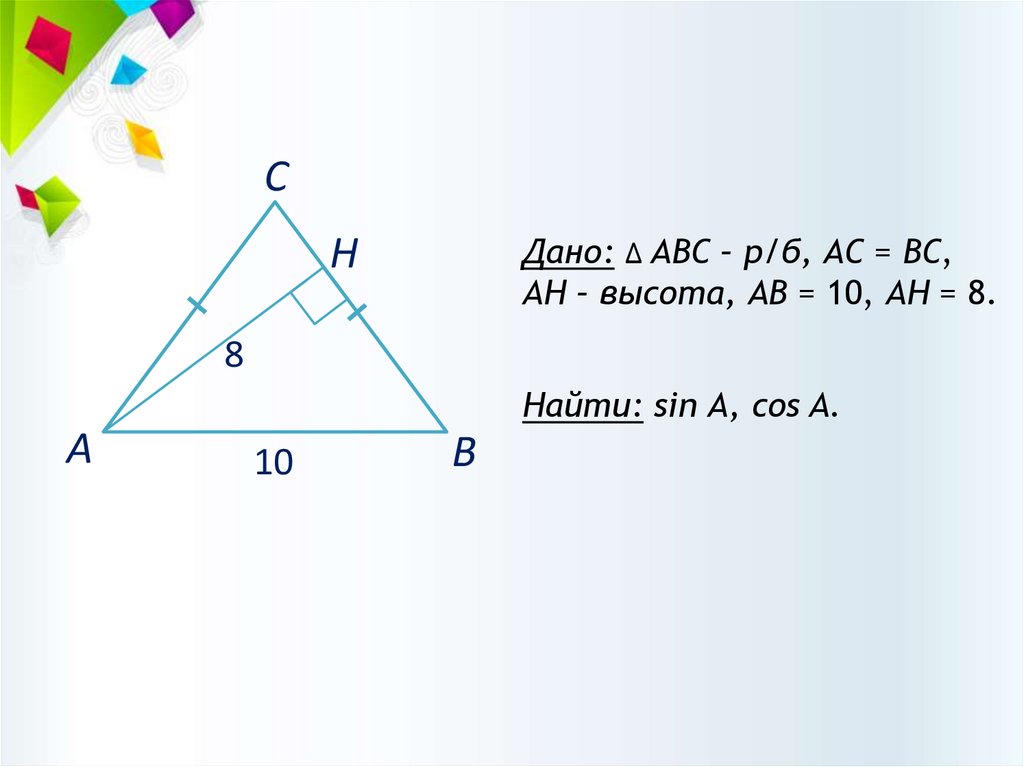
СДано: ∆ АВС – р/б, АС = ВС,
AH – высота, АВ = 10, AH = 8.
Н
8
Найти: sin А, cos A.
А
10
В
33.
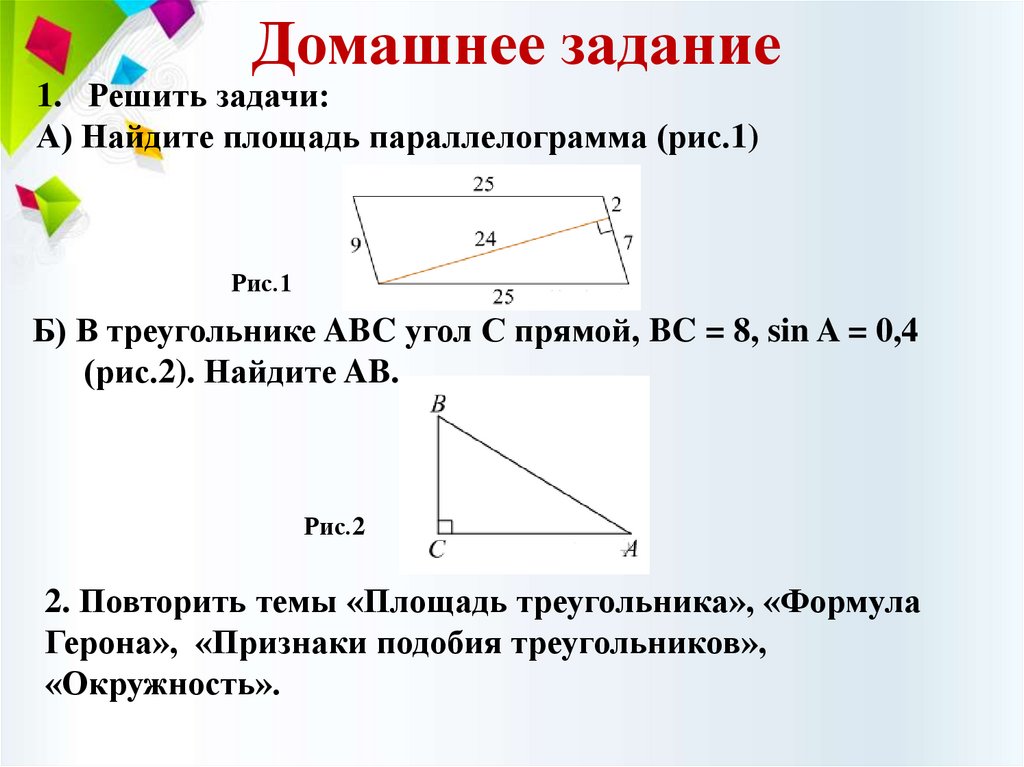
Домашнее задание1. Решить задачи:
А) Найдите площадь параллелограмма (рис.1)
Рис.1
Б) В треугольнике ABC угол С прямой, BC = 8, sin A = 0,4
(рис.2). Найдите AB.
Рис.2
2. Повторить темы «Площадь треугольника», «Формула
Герона», «Признаки подобия треугольников»,
«Окружность».







 mathematics
mathematics








