Similar presentations:
Вводное повторение, геометрия, 9 класс
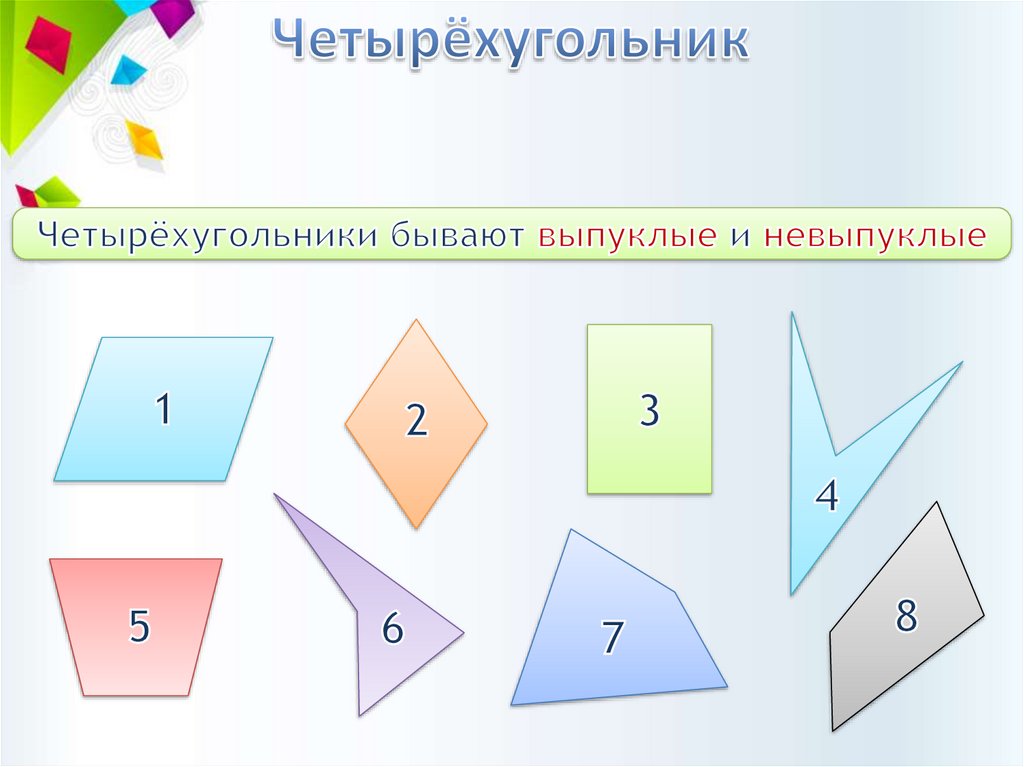
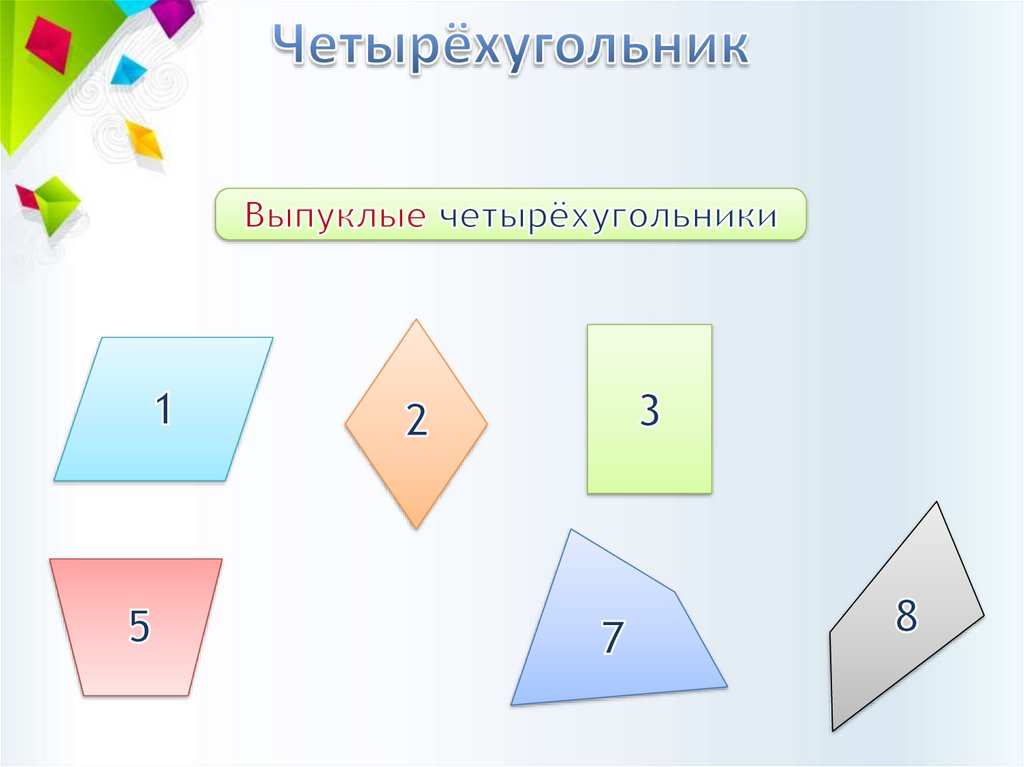
1.
2.
3.
4.
5.
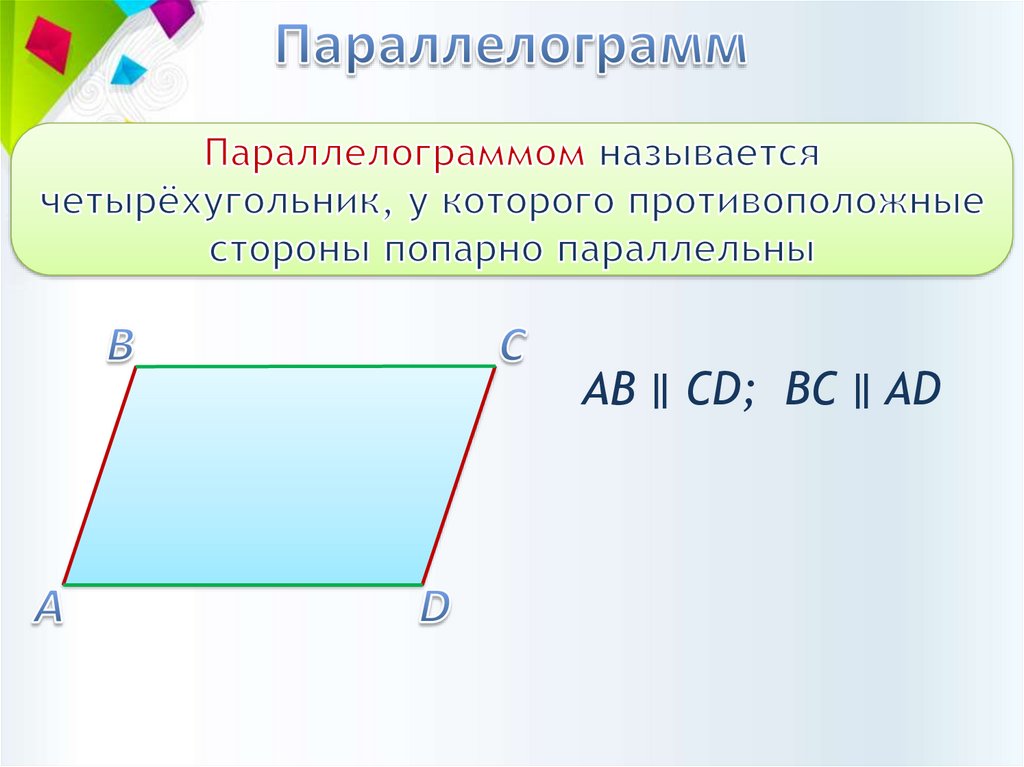
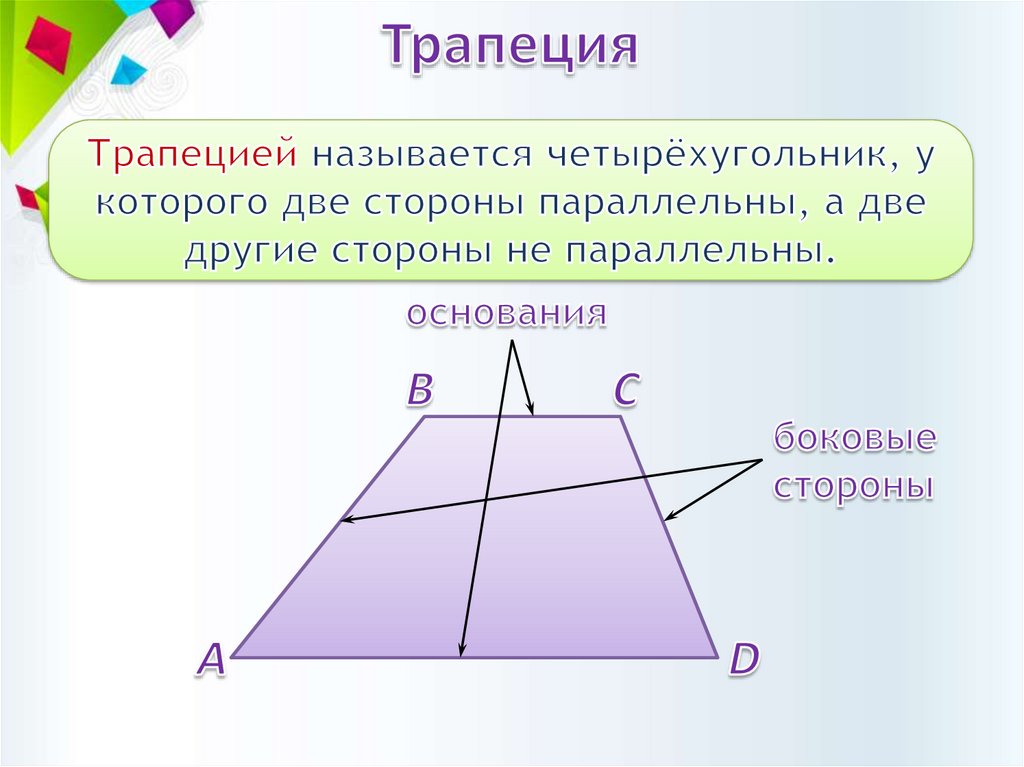
АВ ∥ CD; BC ∥ AD6.
7.
8.
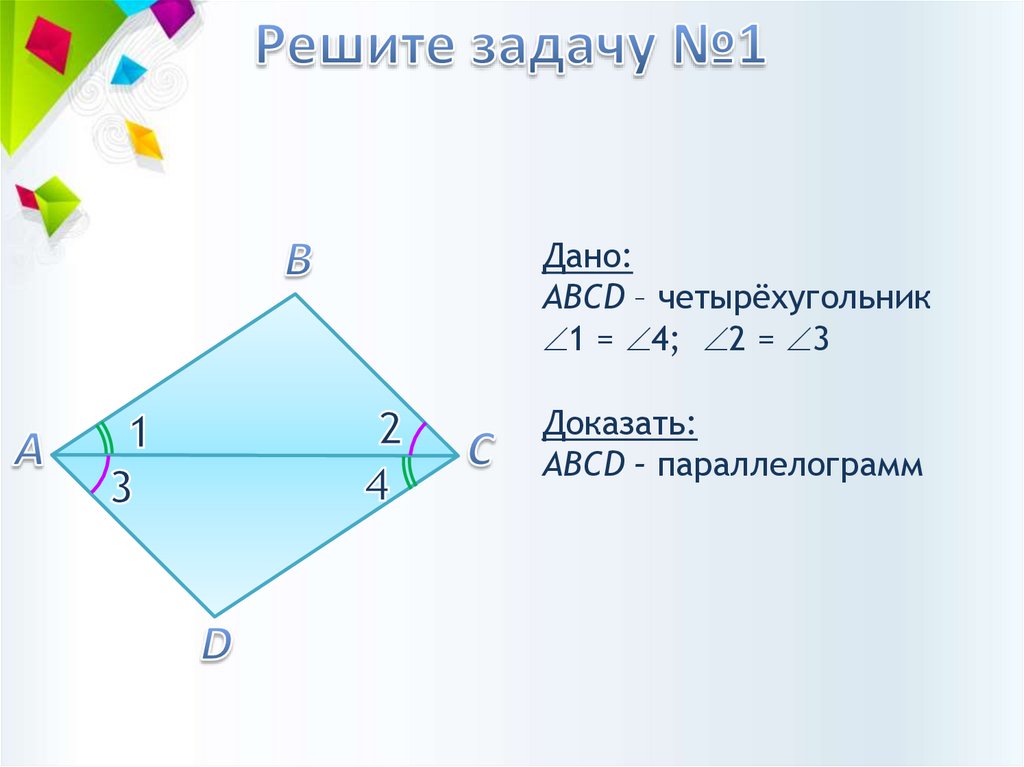
Дано:АВCD – четырёхугольник
1 = 4; 2 = 3
Доказать:
АВCD – параллелограмм
9.
10.
11.
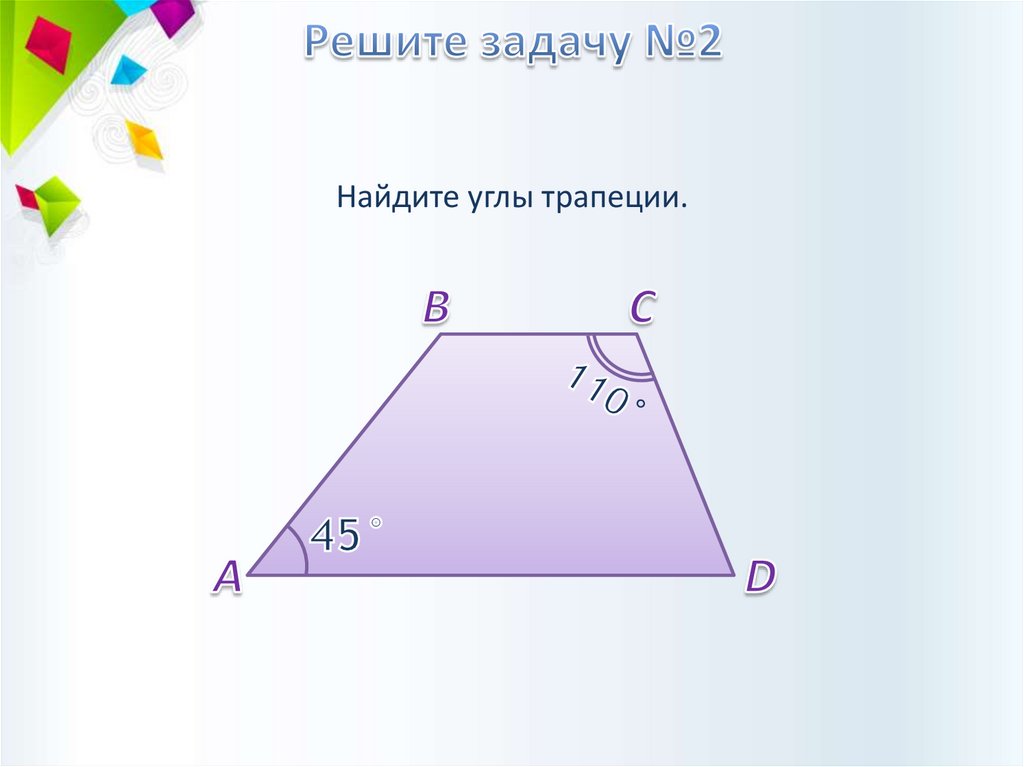
Найдите углы трапеции.12.
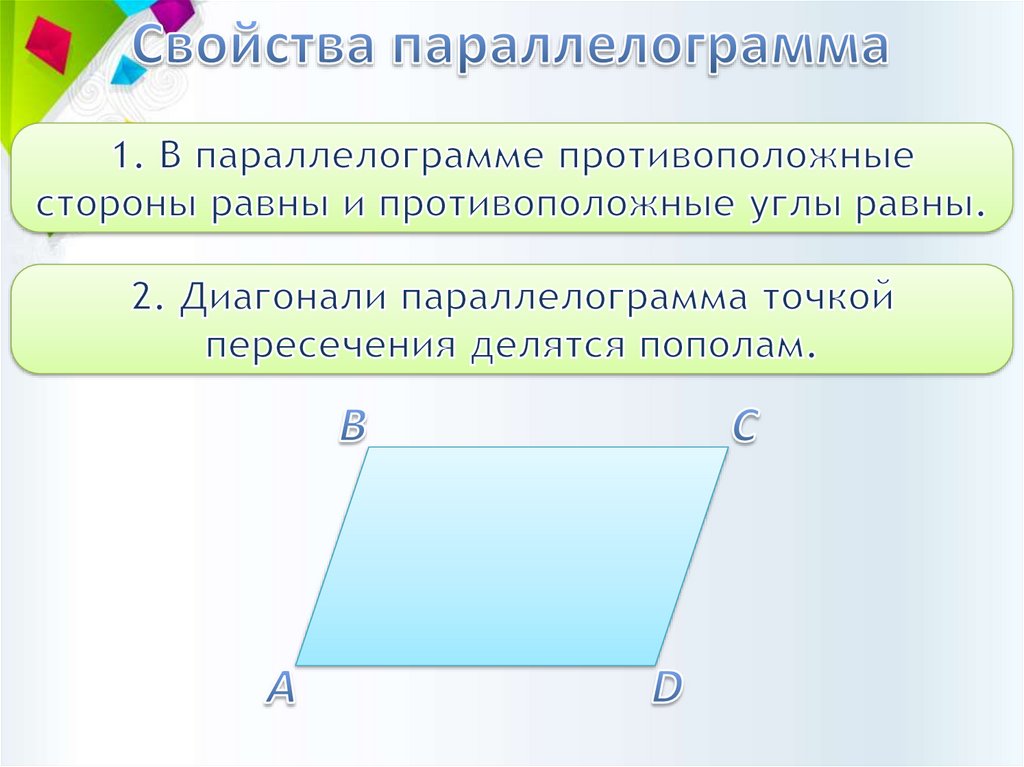
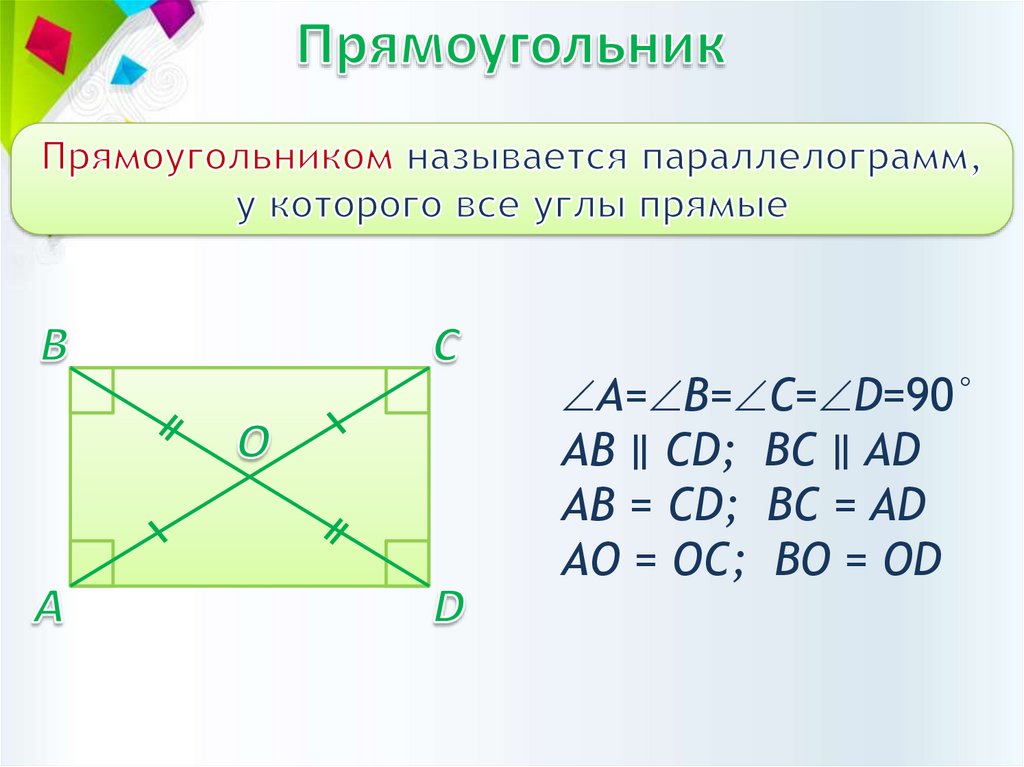
А= В= С= D=90°АВ ∥ CD; BC ∥ AD
АВ = CD; BC = AD
АО = ОC; BО = ОD
13.
14.
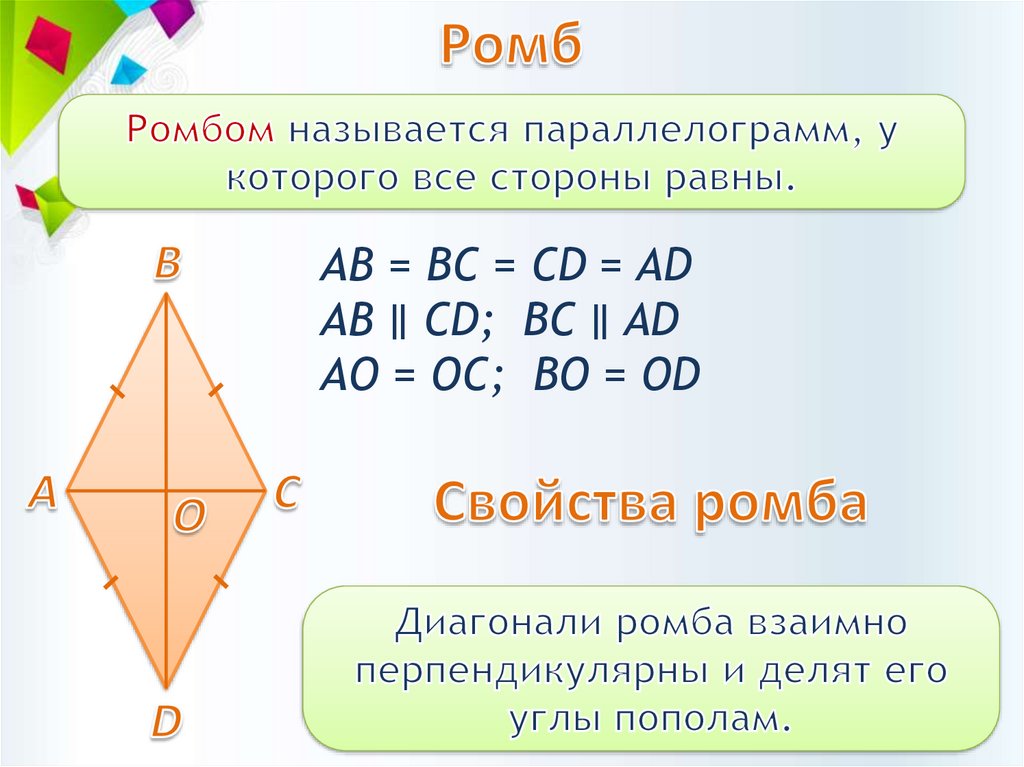
АВ = BC = CD = ADАВ ∥ CD; BC ∥ AD
АО = ОC; BО = ОD
15.
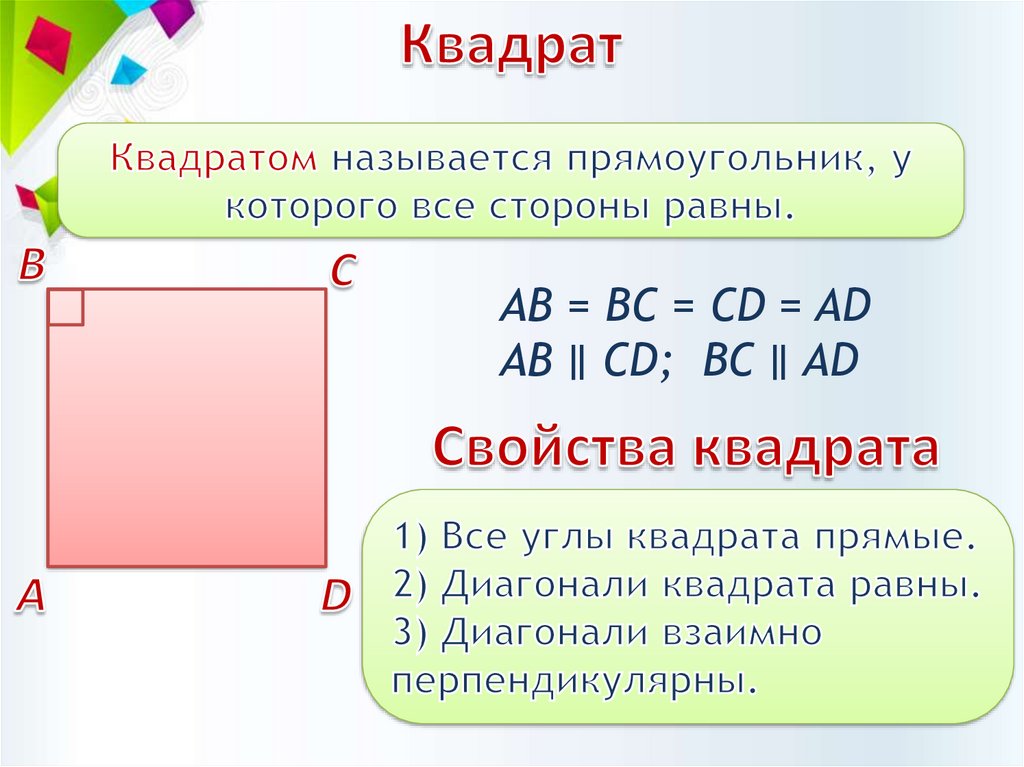
АВ = BC = CD = ADАВ ∥ CD; BC ∥ AD
16.
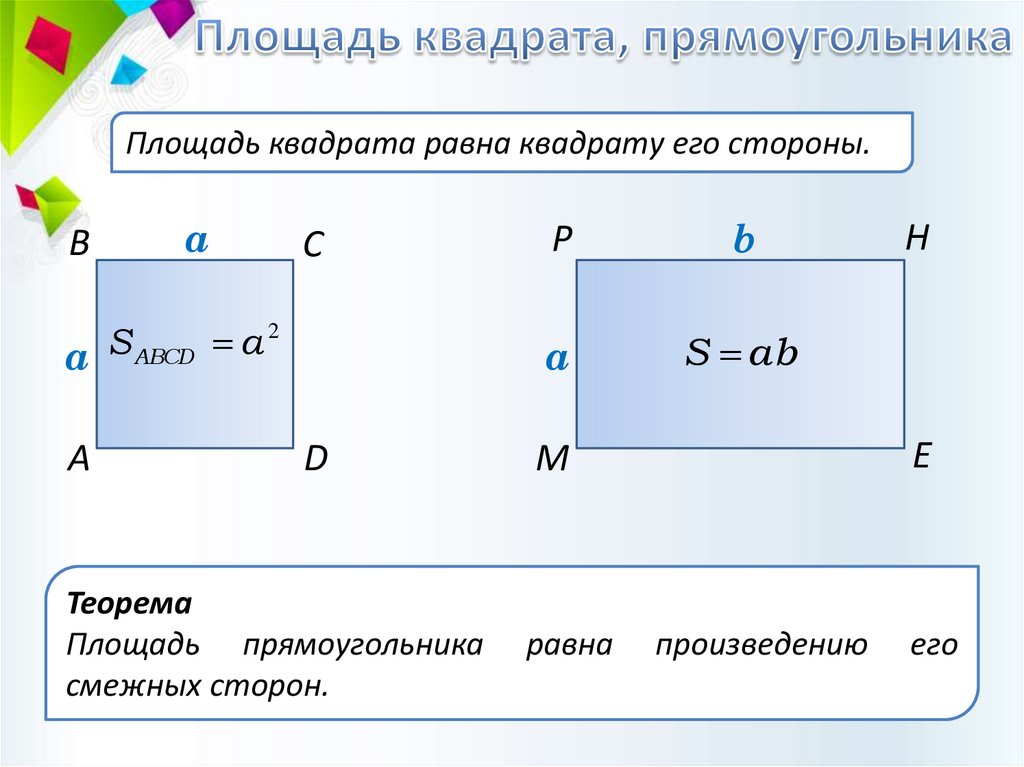
Площадь квадрата равна квадрату его стороны.B
a
C
2
S
a
a ABCD
A
D
Теорема
Площадь прямоугольника
смежных сторон.
Р
b
a
S ab
Е
М
равна
Н
произведению
его
17.
B7
P
5
C
Дано: ABCD – прямоугольник
1 = 2, BP = 7, РC = 5
1
2
A
D
Найти: SABCD
18.
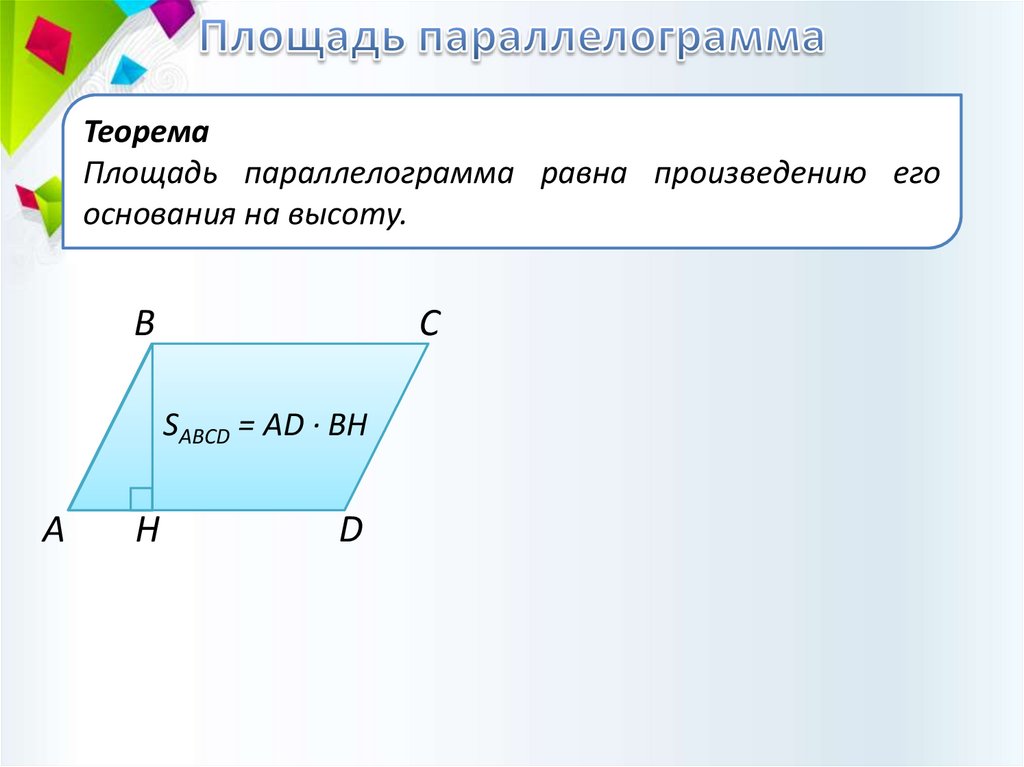
ТеоремаПлощадь параллелограмма равна произведению его
основания на высоту.
B
C
SABCD = AD · BH
A
Н
D
19.
BC
15
12
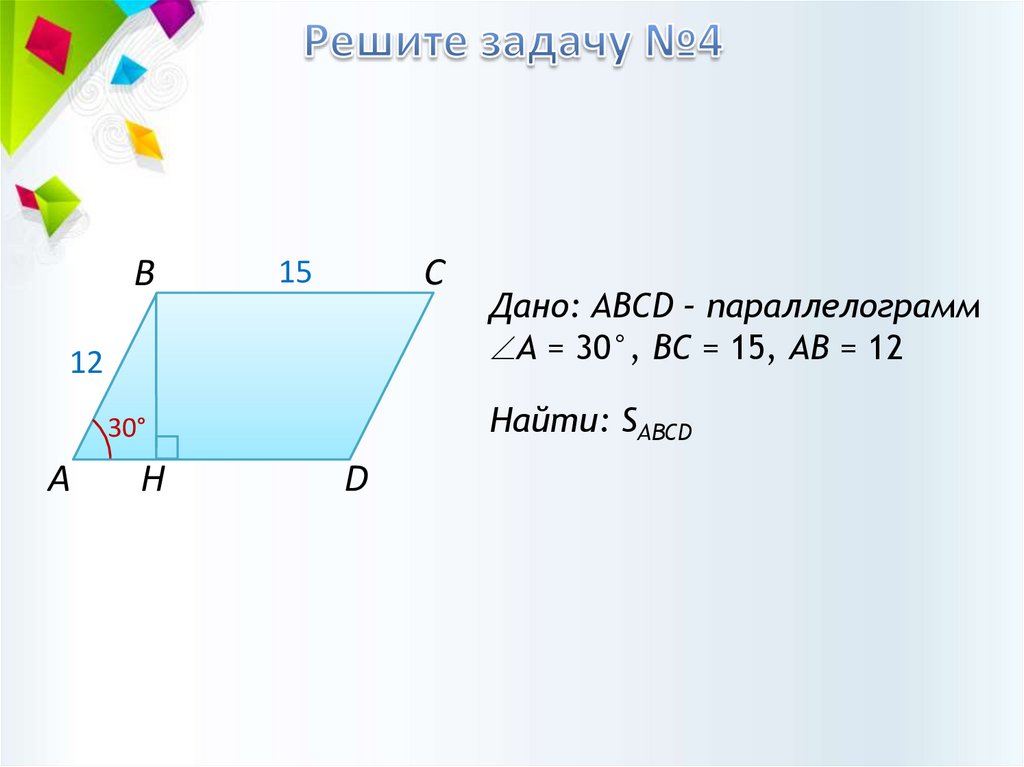
Найти: SABCD
30°
A
Н
Дано: ABCD – параллелограмм
А = 30°, BС = 15, АВ = 12
D
20.
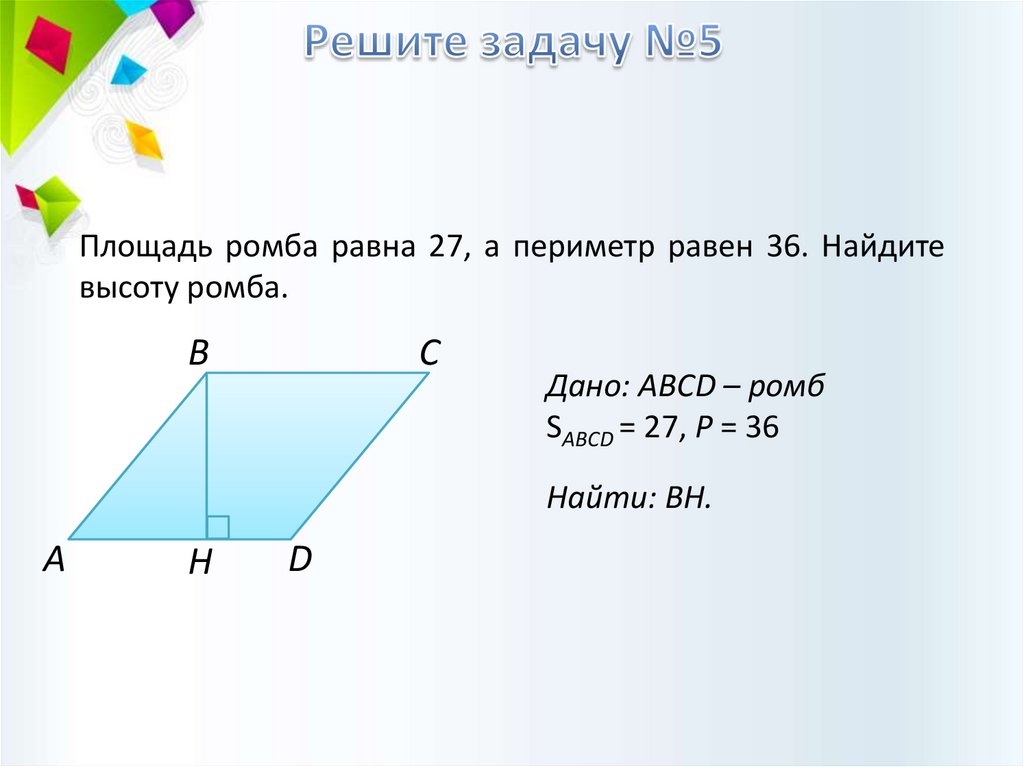
Площадь ромба равна 27, а периметр равен 36. Найдитевысоту ромба.
B
C
Дано: ABCD – ромб
SАBCD = 27, P = 36
Найти: BH.
A
Н
D
21.
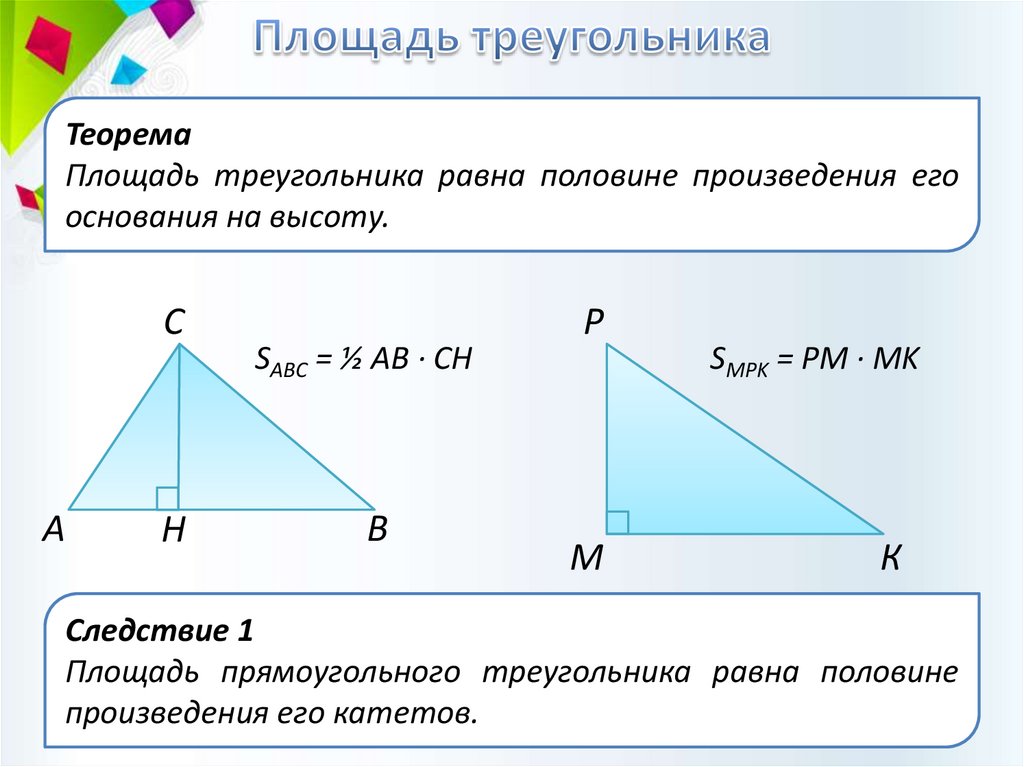
ТеоремаПлощадь треугольника равна половине произведения его
основания на высоту.
C
A
Н
SABC = ½ AB · CH
B
Р
М
SMPK = PM · MK
К
Следствие 1
Площадь прямоугольного треугольника равна половине
произведения его катетов.
22.
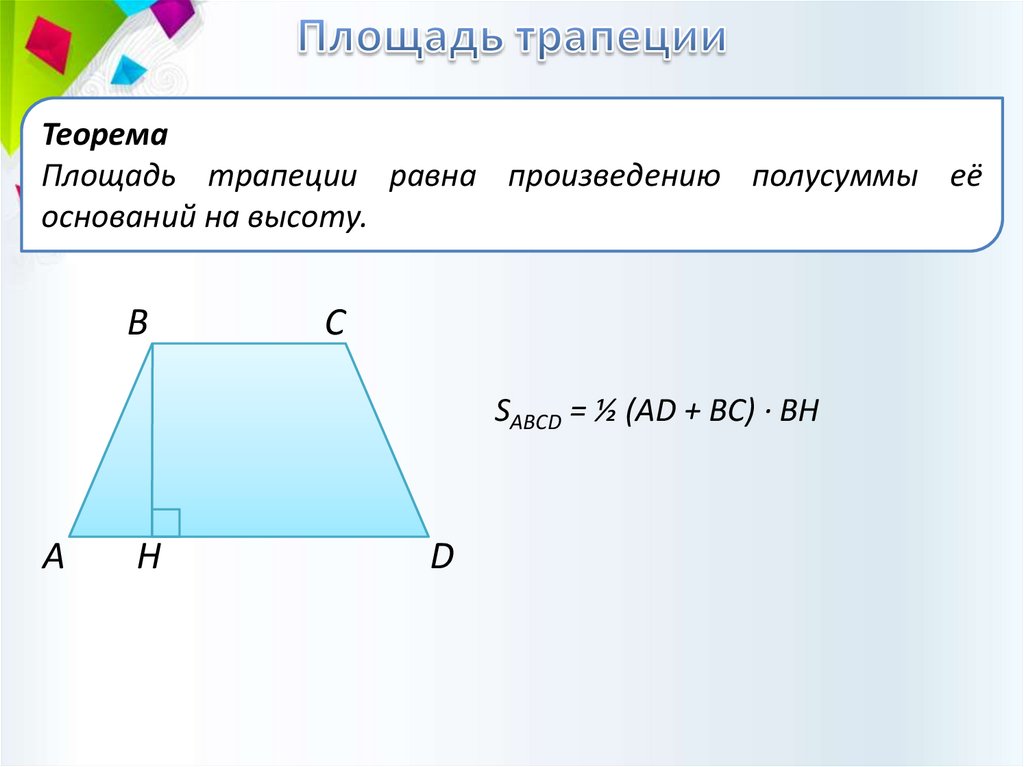
ТеоремаПлощадь трапеции равна произведению полусуммы её
оснований на высоту.
В
С
SABCD = ½ (AD + BC) · BH
A
Н
D
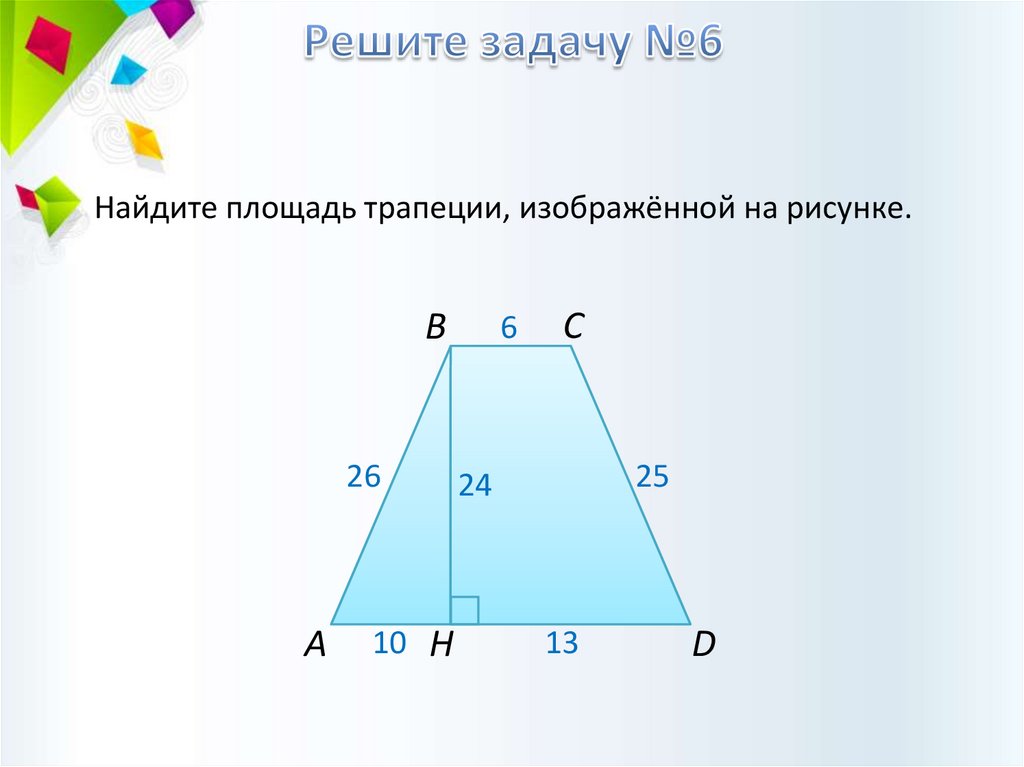
23.
Найдите площадь трапеции, изображённой на рисунке.В
26
A
10 Н
6
С
25
24
13
D
24.
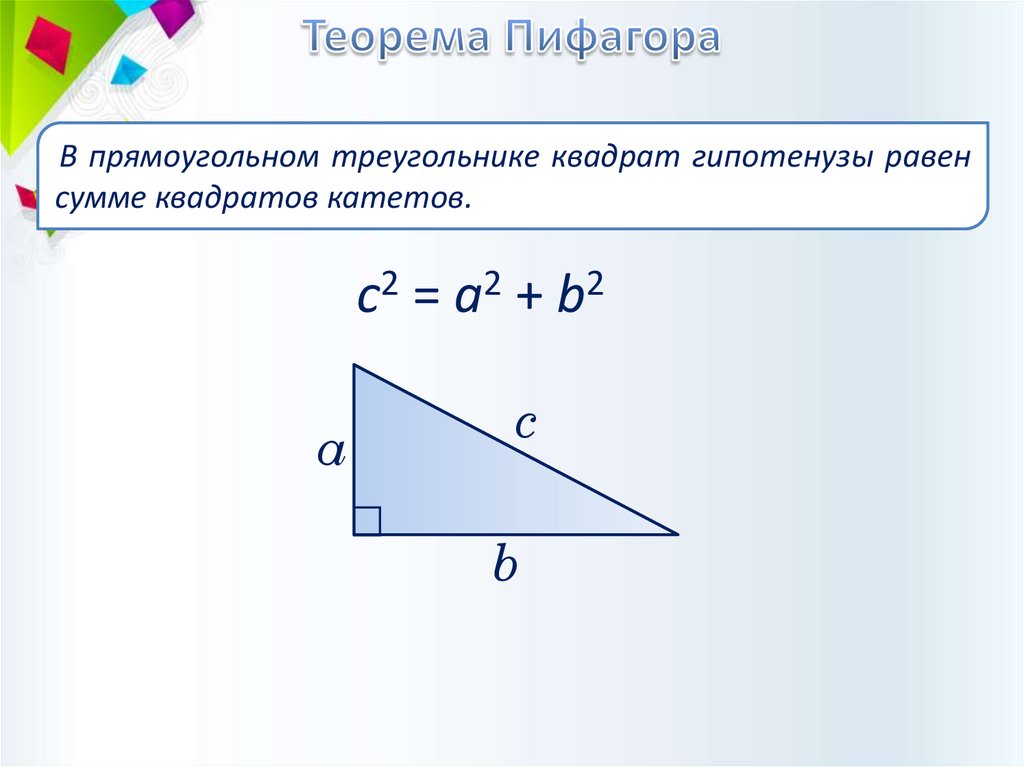
В прямоугольном треугольнике квадрат гипотенузы равенсумме квадратов катетов.
c2 = a2 + b2
a
c
b
25.
Если два угла одного треугольника соответственно равныдвум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, заключенные
между этими сторонами, равны, то такие треугольники
подобны.
Если три стороны одного треугольника пропорциональны
трем сторонам другого треугольника, то такие
треугольники подобны.
26.
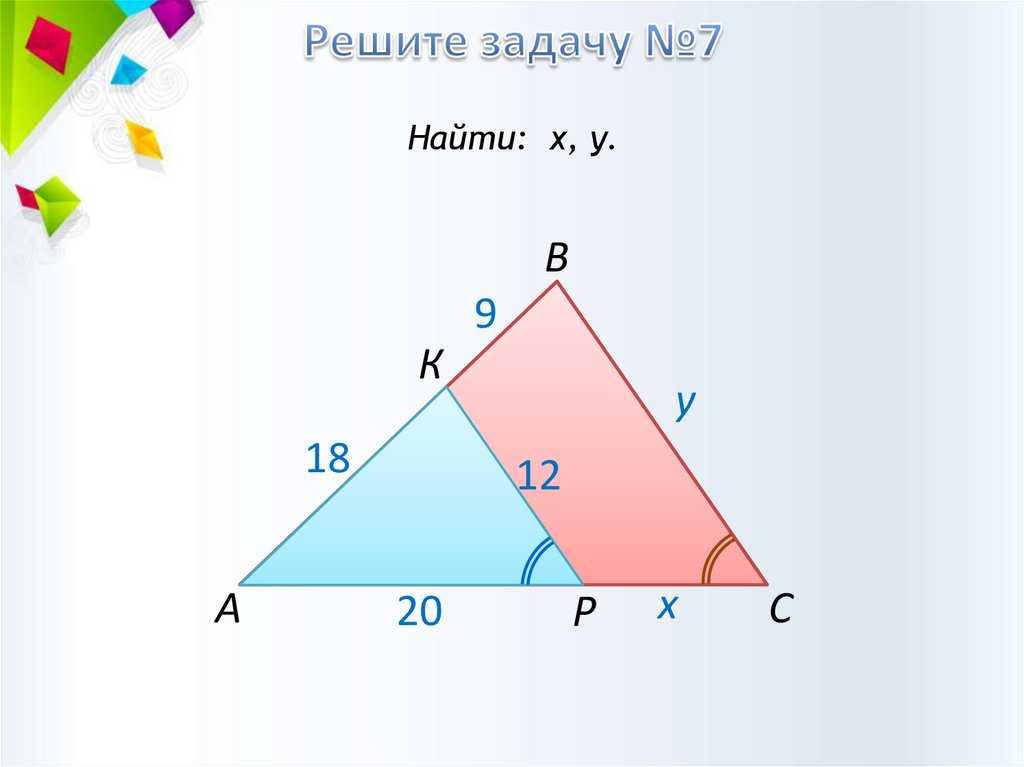
Найти: х, у.В
9
К
18
А
у
12
20
Р
х
С
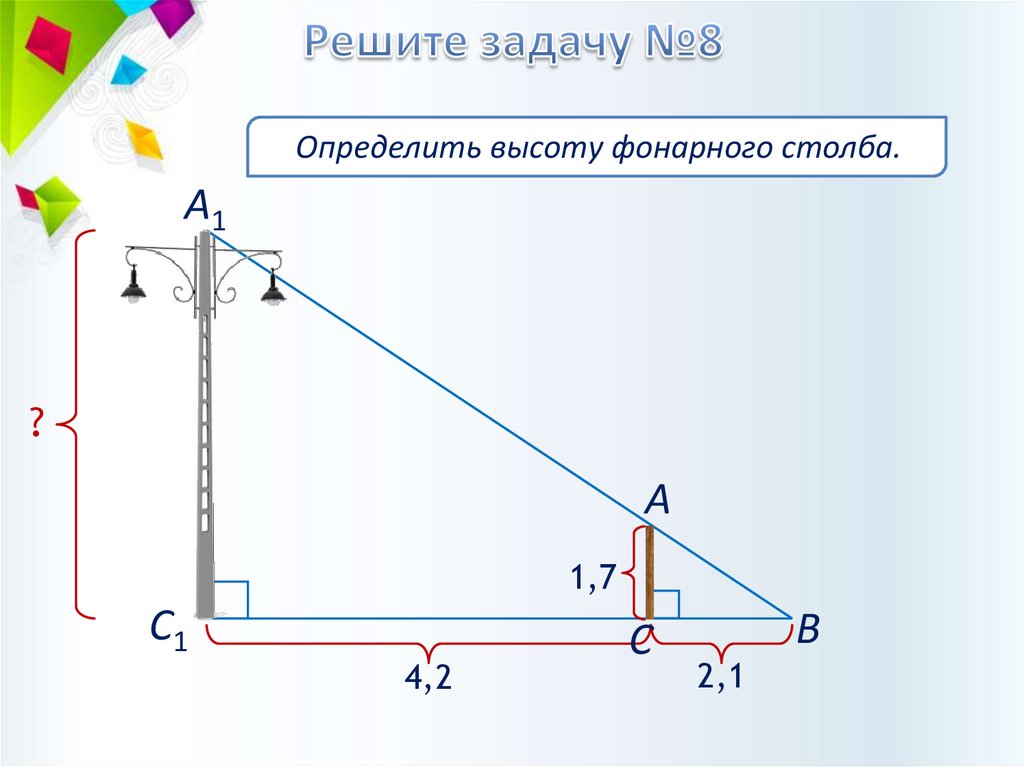
27.
Определить высоту фонарного столба.А1
?
А
1,7
С1
4,2
С
В
2,1
28.
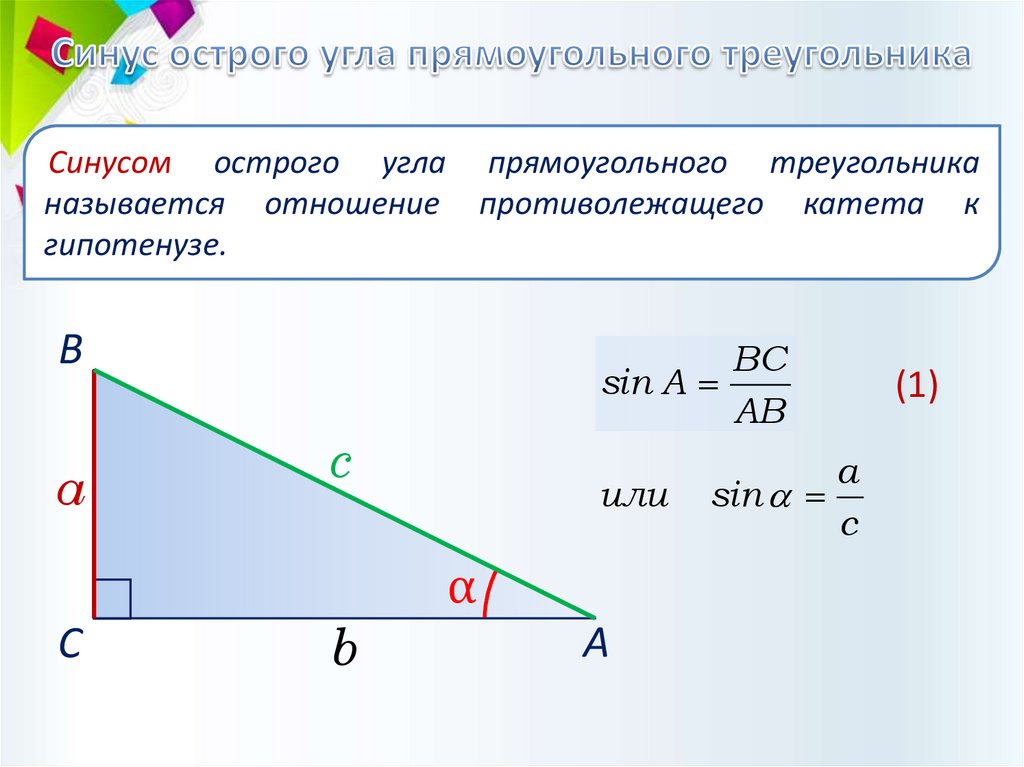
Синусом острого угла прямоугольного треугольниканазывается отношение противолежащего катета к
гипотенузе.
В
a
BC
sin A
AB
c
или
α
С
b
А
a
sin
c
(1)
29.
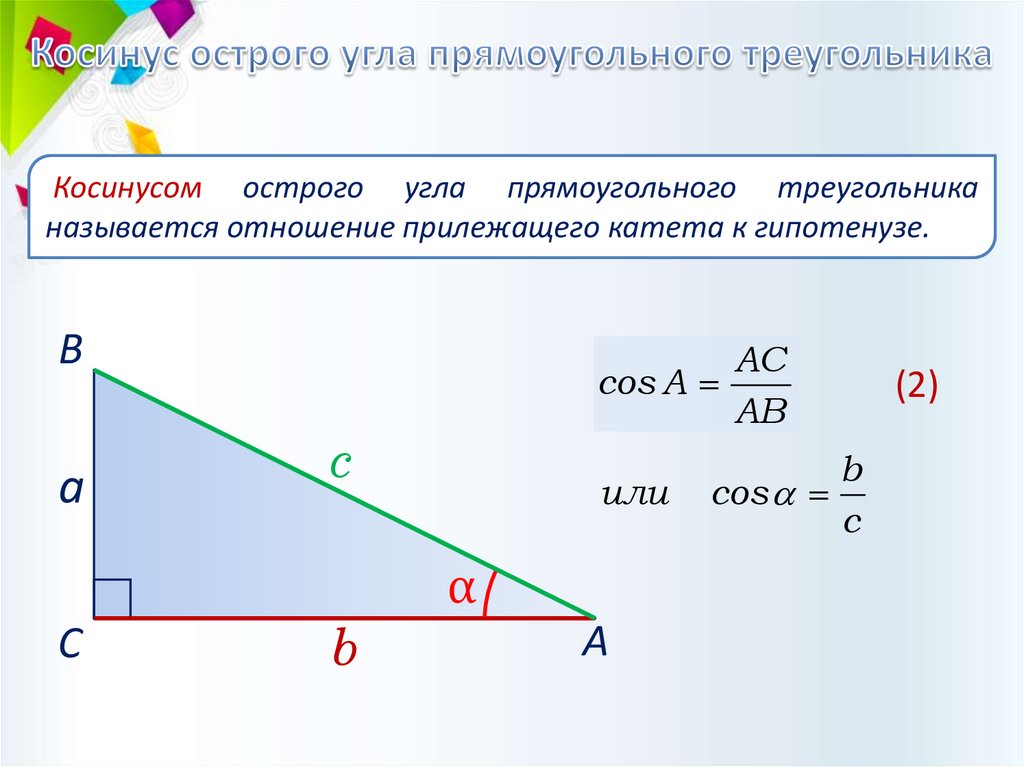
Косинусом острого угла прямоугольного треугольниканазывается отношение прилежащего катета к гипотенузе.
В
a
AC
cos A
AB
c
или
α
С
b
А
b
cos
c
(2)
30.
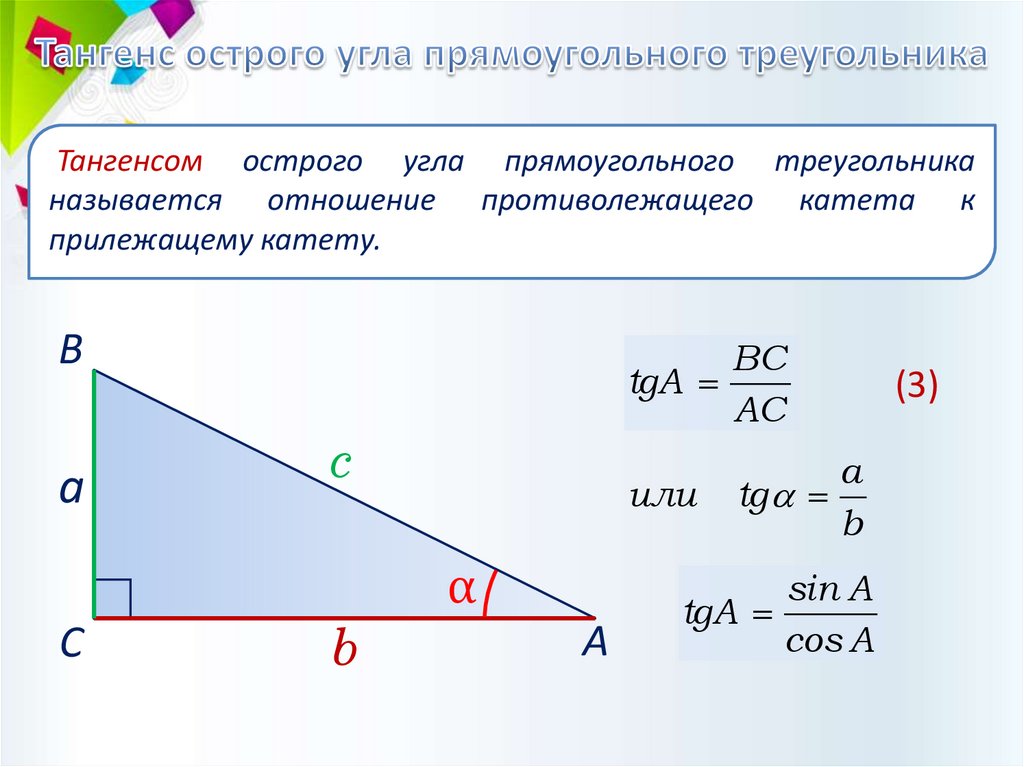
Тангенсом острого угла прямоугольного треугольниканазывается отношение противолежащего катета к
прилежащему катету.
В
a
BC
tgA
AC
c
или
α
С
b
А
a
tg
b
sin A
tgA
cos A
(3)
31.
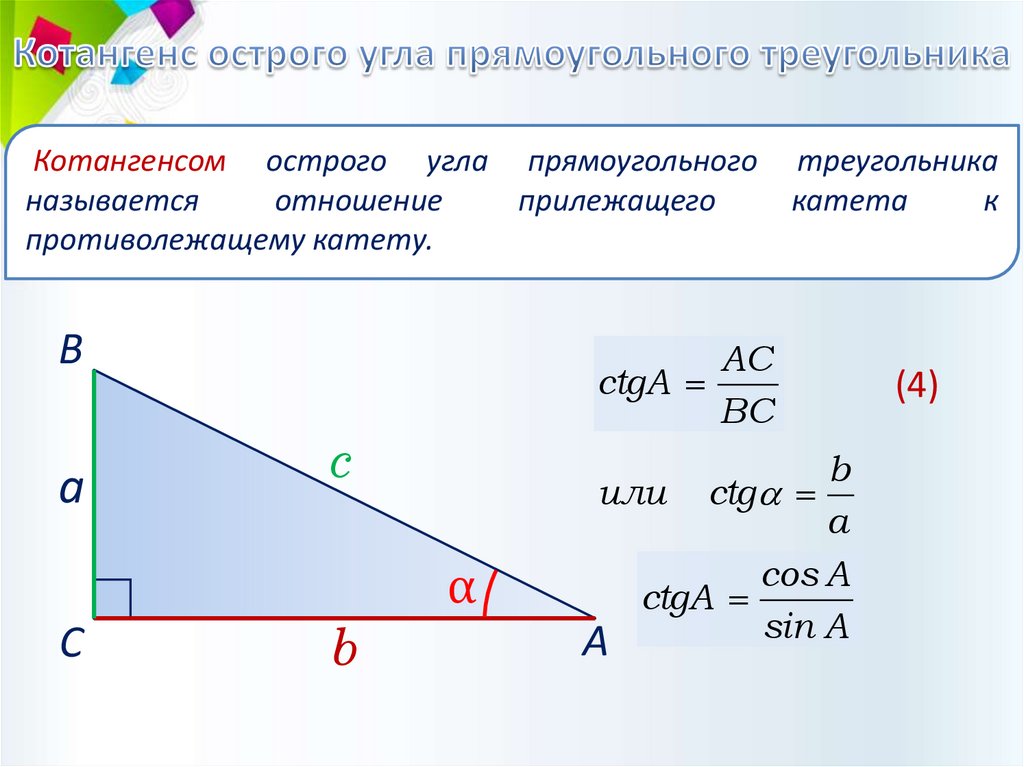
Котангенсом острого угла прямоугольногоназывается
отношение
прилежащего
противолежащему катету.
В
a
АC
сtgA
ВC
c
α
С
b
треугольника
катета
к
b
или сtg
а
cos A
сtgA
sin A
А
(4)
32.
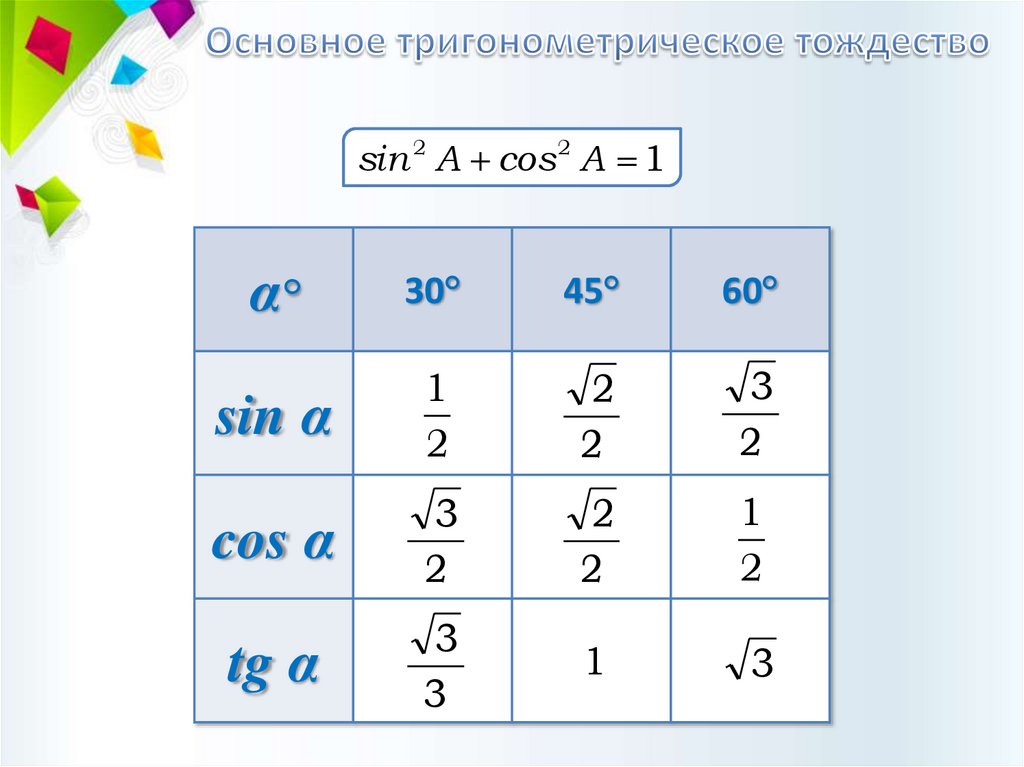
sin 2 A cos 2 A 1α°
30°
45°
60°
sin α
1
2
2
2
3
2
cos α
3
2
2
2
1
2
tg α
3
3
1
3
33.
В6
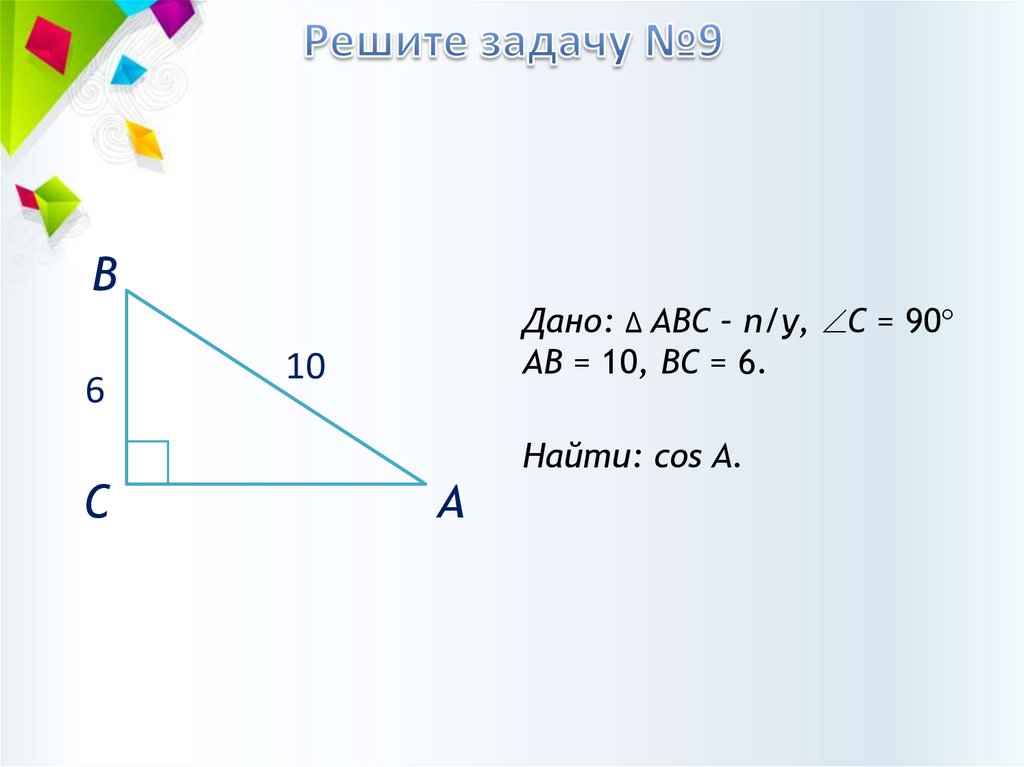
Дано: ∆ АВС – п/у, С = 90
АВ = 10, ВС = 6.
10
Найти: cos A.
С
А
34.
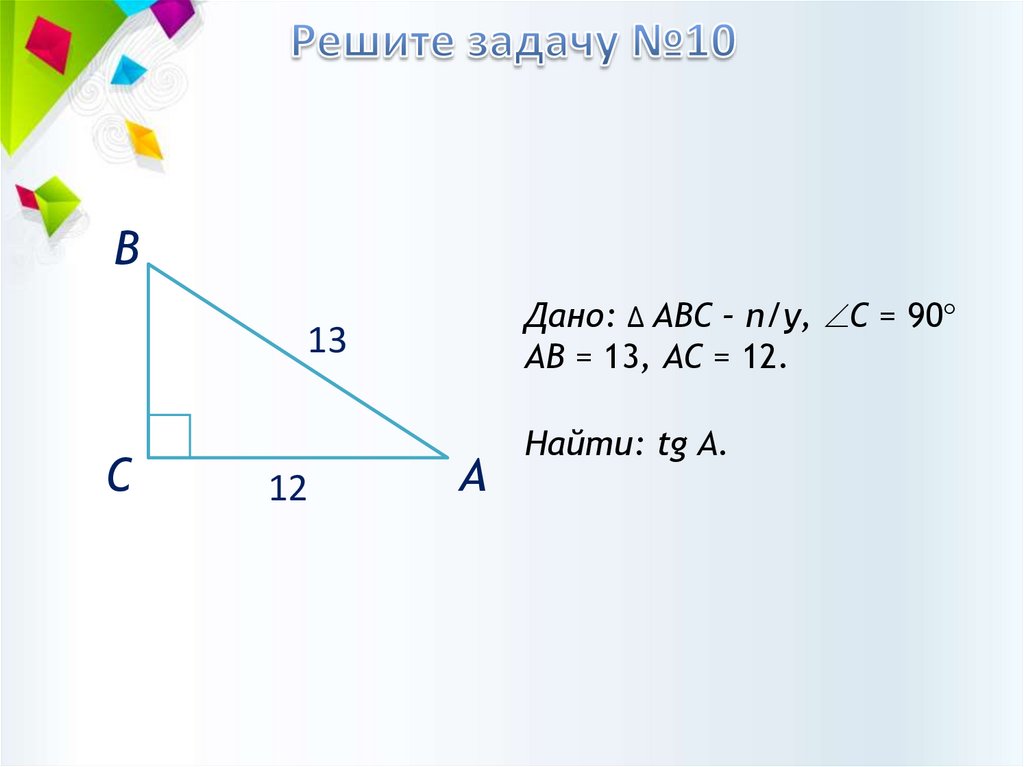
ВДано: ∆ АВС – п/у, С = 90
АВ = 13, АС = 12.
13
С
12
А
Найти: tg A.
35.
ВH
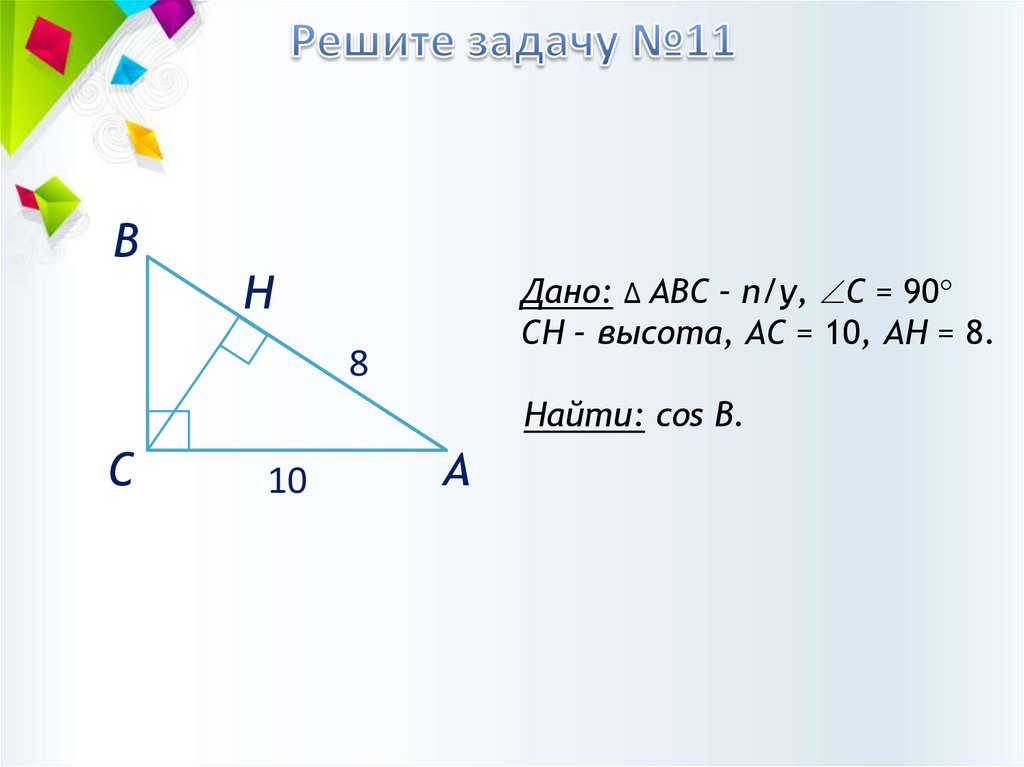
Дано: ∆ АВС – п/у, С = 90
CH – высота, АС = 10, АН = 8.
8
Найти: cos B.
С
10
А
36.
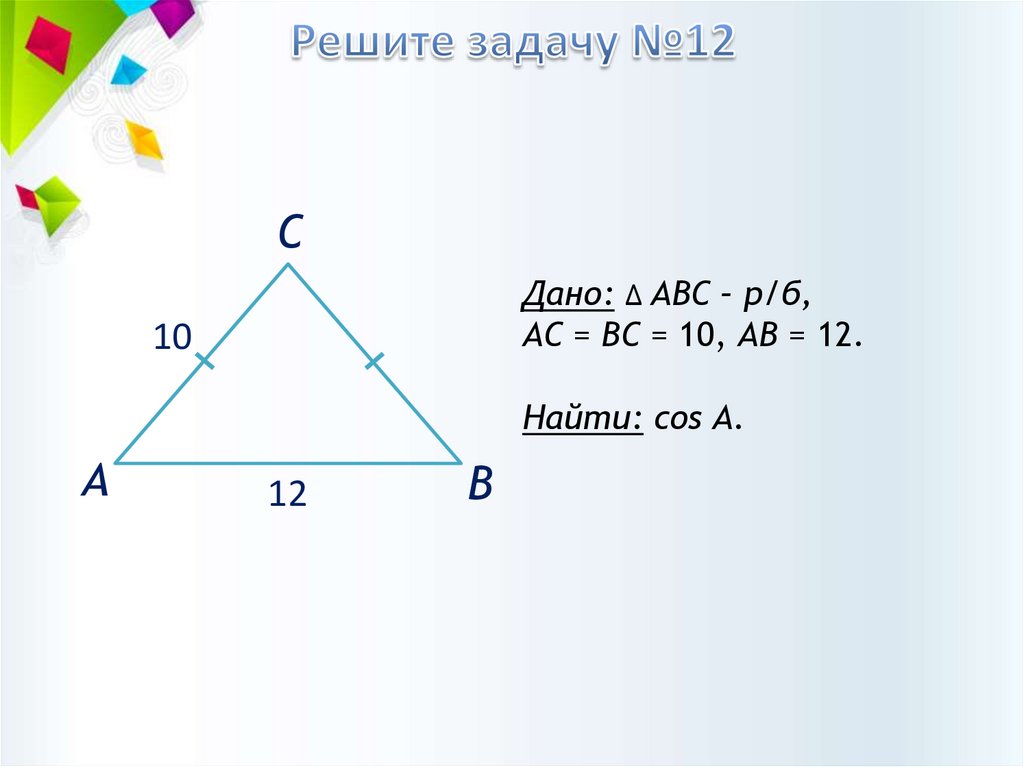
СДано: ∆ АВС – р/б,
АС = ВС = 10, АВ = 12.
10
Найти: cos А.
А
12
В
37.
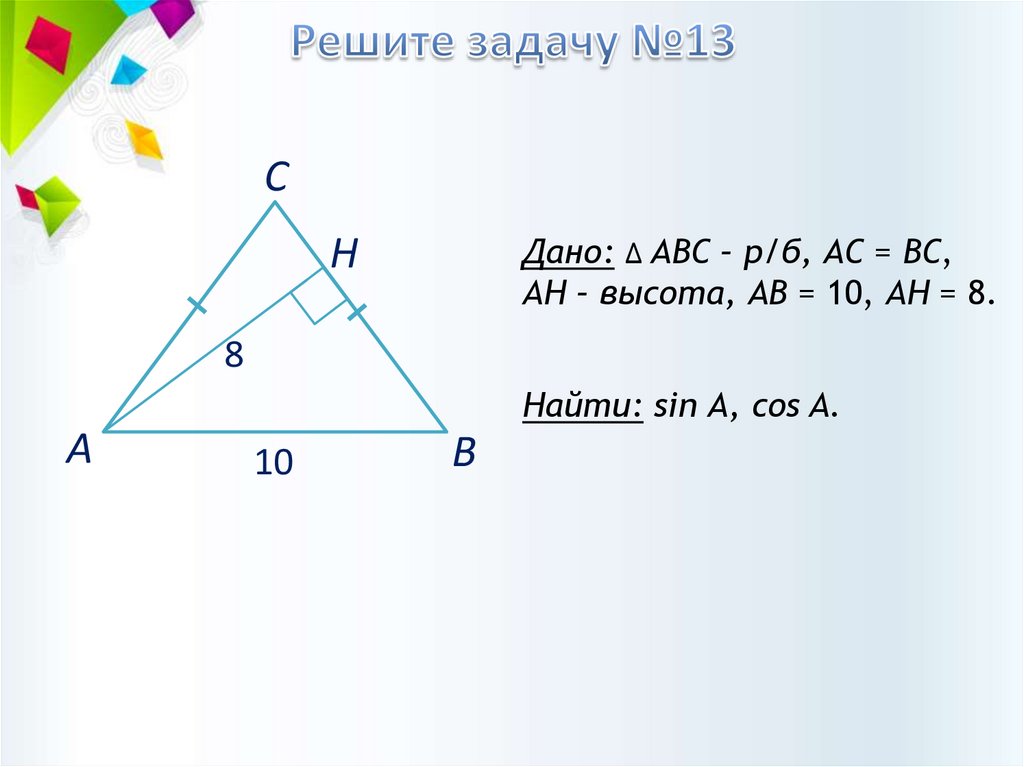
СДано: ∆ АВС – р/б, АС = ВС,
AH – высота, АВ = 10, AH = 8.
Н
8
Найти: sin А, cos A.
А
10
В
38.
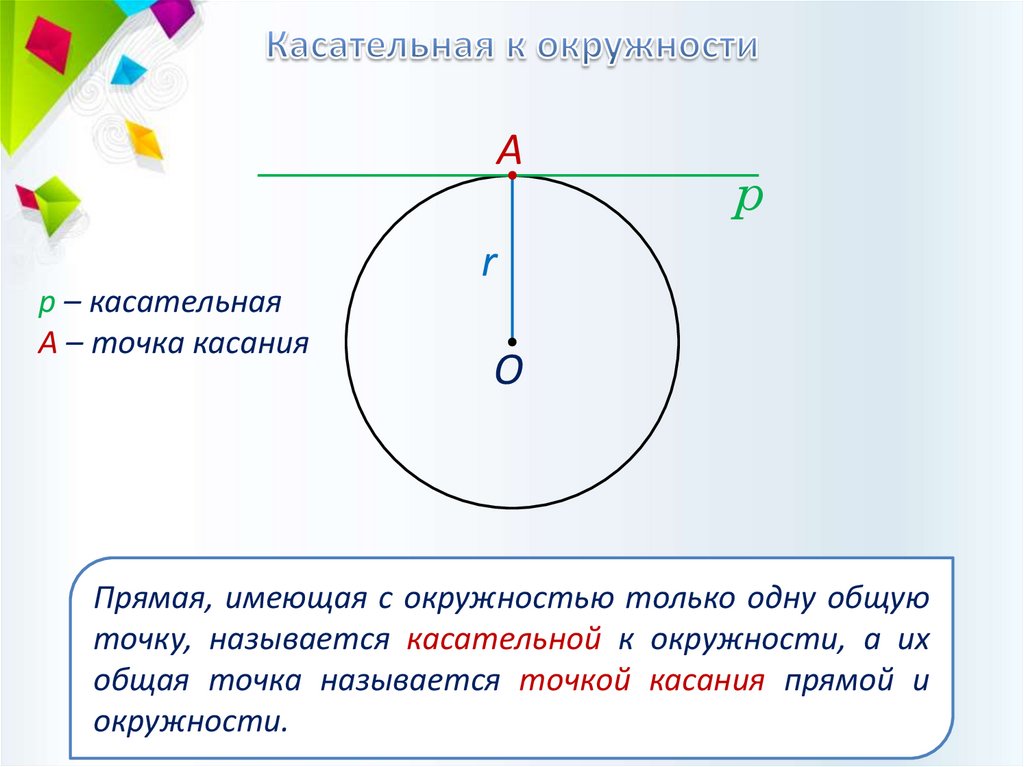
Ар – касательная
А – точка касания
р
r
О
Прямая, имеющая с окружностью только одну общую
точку, называется касательной к окружности, а их
общая точка называется точкой касания прямой и
окружности.
39.
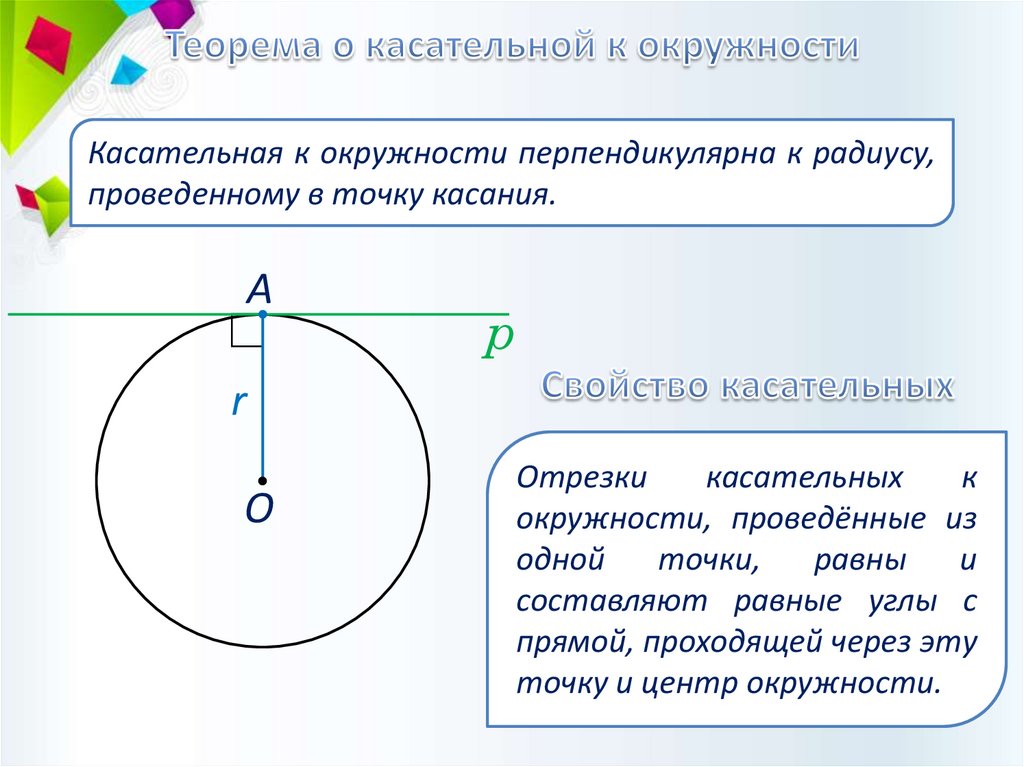
Касательная к окружности перпендикулярна к радиусу,проведенному в точку касания.
А
р
r
О
Отрезки
касательных
к
окружности, проведённые из
одной
точки,
равны
и
составляют равные углы с
прямой, проходящей через эту
точку и центр окружности.
40.
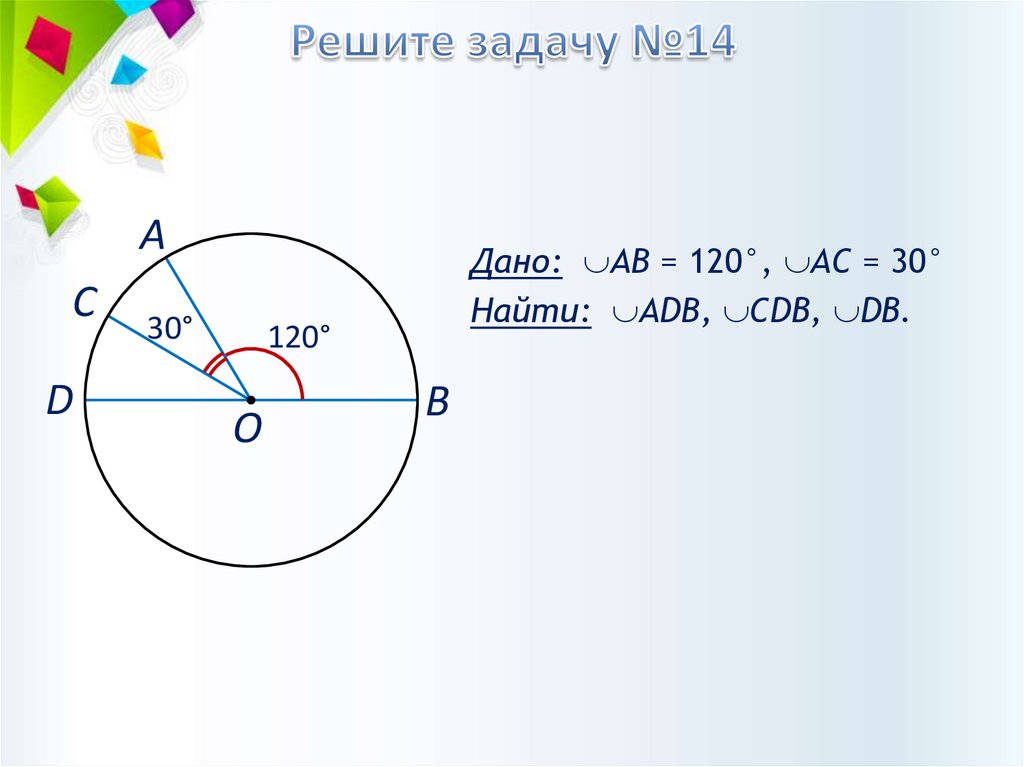
АС
D
30°
Дано: АВ = 120°, AC = 30°
Найти: АDВ, CDB, DB.
120°
О
В
41.
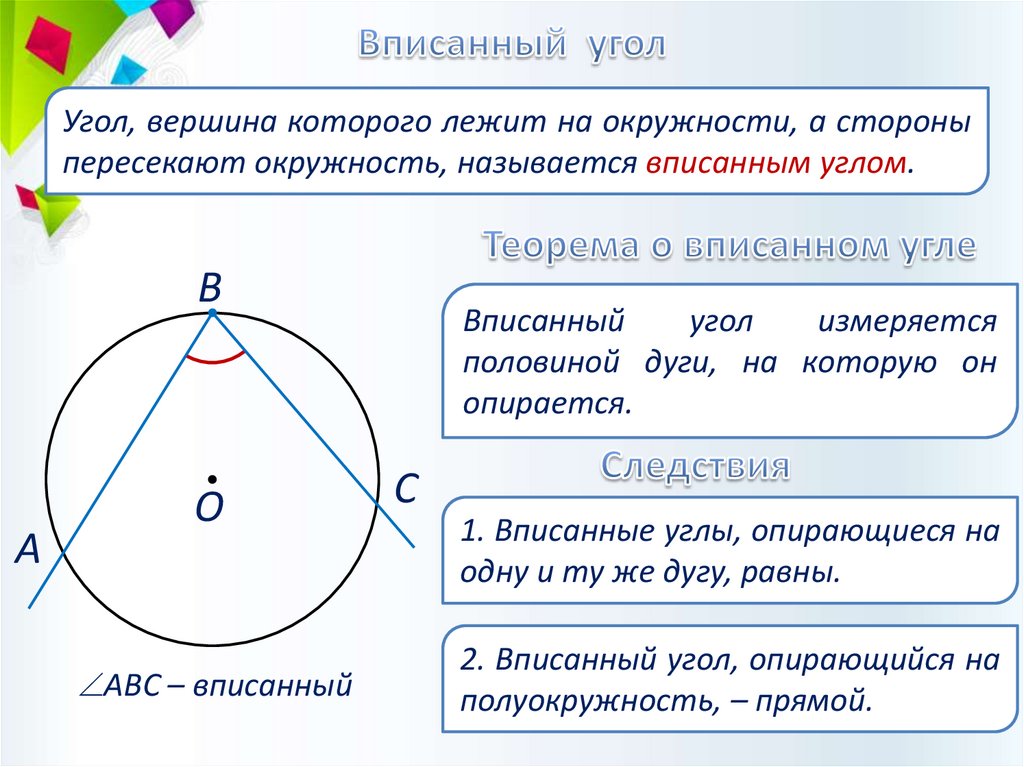
Угол, вершина которого лежит на окружности, а стороныпересекают окружность, называется вписанным углом.
В
А
О
АВС – вписанный
Вписанный
угол
измеряется
половиной дуги, на которую он
опирается.
С
1. Вписанные углы, опирающиеся на
одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на
полуокружность, – прямой.
42.
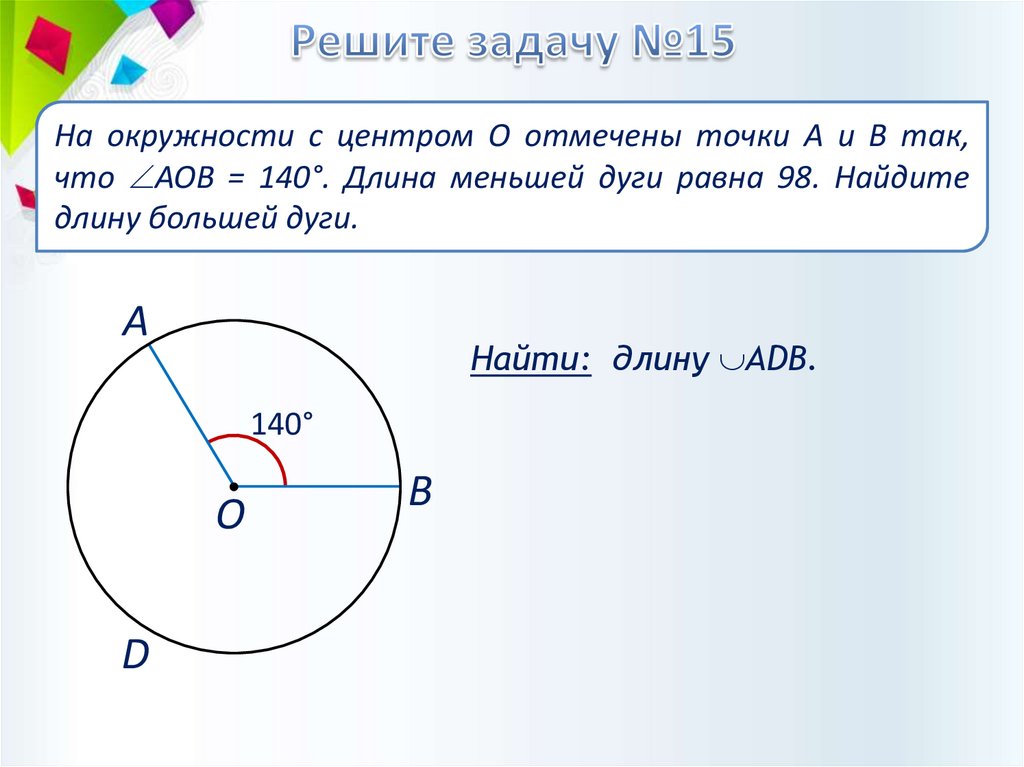
На окружности с центром О отмечены точки А и В так,что АОВ = 140°. Длина меньшей дуги равна 98. Найдите
длину большей дуги.
А
Найти: длину АDВ.
140°
О
D
В
43.
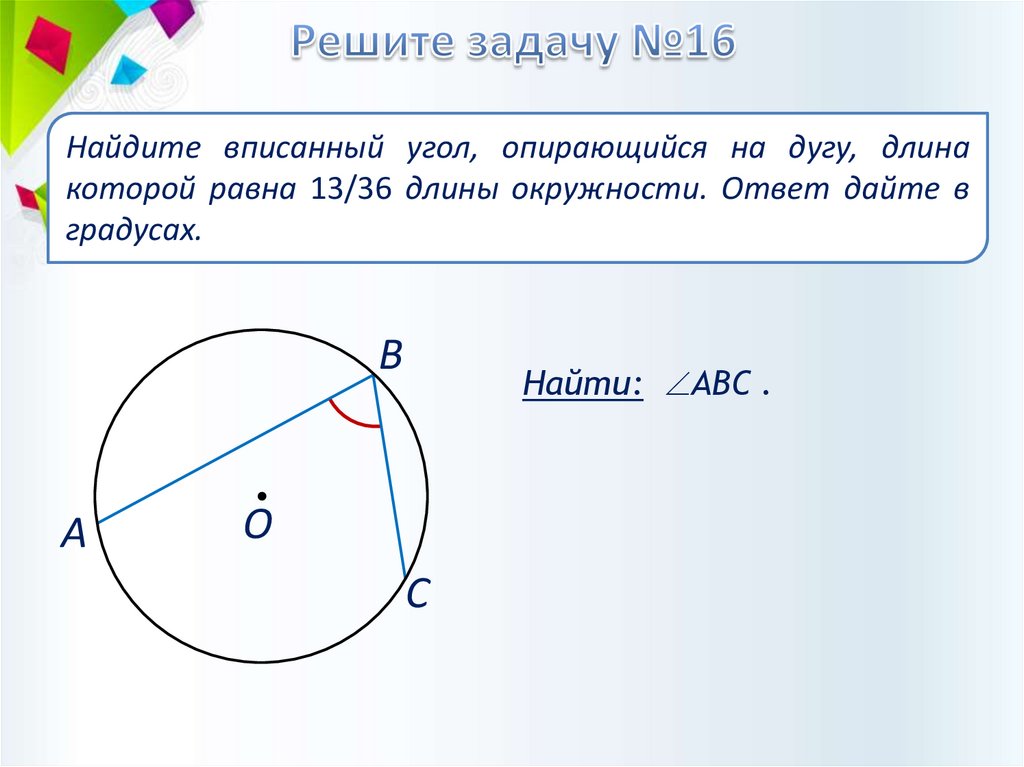
Найдите вписанный угол, опирающийся на дугу, длинакоторой равна 13/36 длины окружности. Ответ дайте в
градусах.
В
А
Найти: АВС .
О
С
44.
Свойство биссектрисыТеорема. Каждая точка биссектрисы неразвёрнутого
угла равноудалена от его сторон.
Обратно:
• Каждая точка, лежащая внутри угла и равноудалённая
от сторон угла, лежит на его биссектрисе.
45.
Следствие:Биссектрисы треугольника
пересекаются в одной
точке.
46.
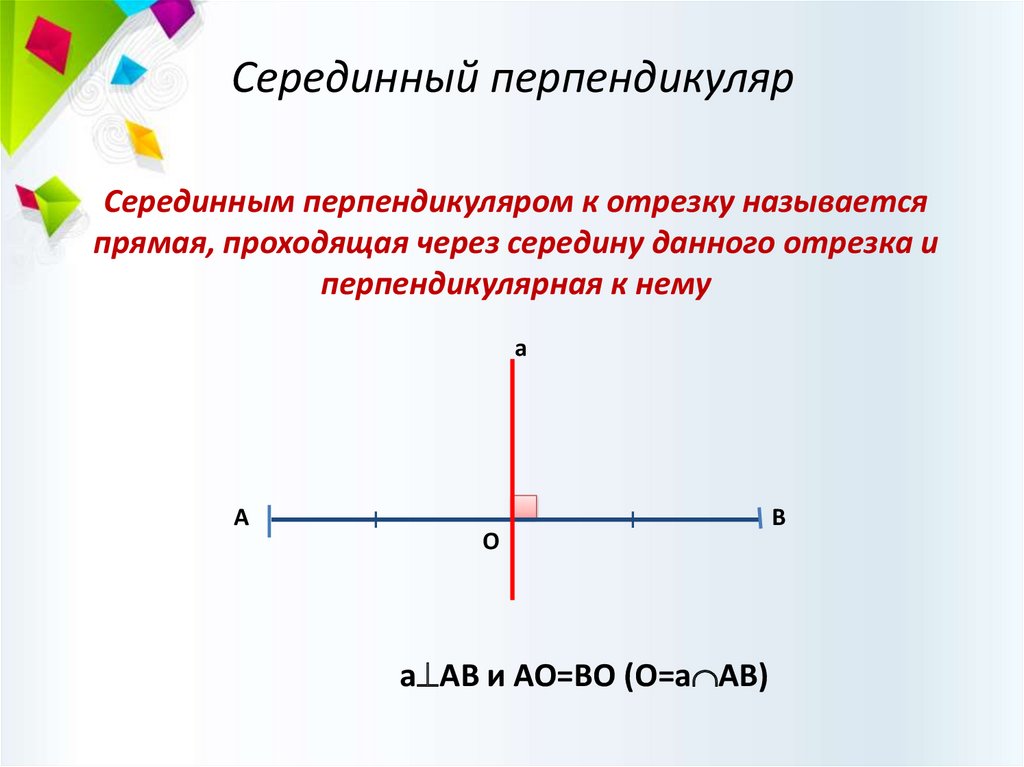
Серединный перпендикулярСерединным перпендикуляром к отрезку называется
прямая, проходящая через середину данного отрезка и
перпендикулярная к нему
a
A
O
а АВ и АО=ВО (О=а АВ)
B
47.
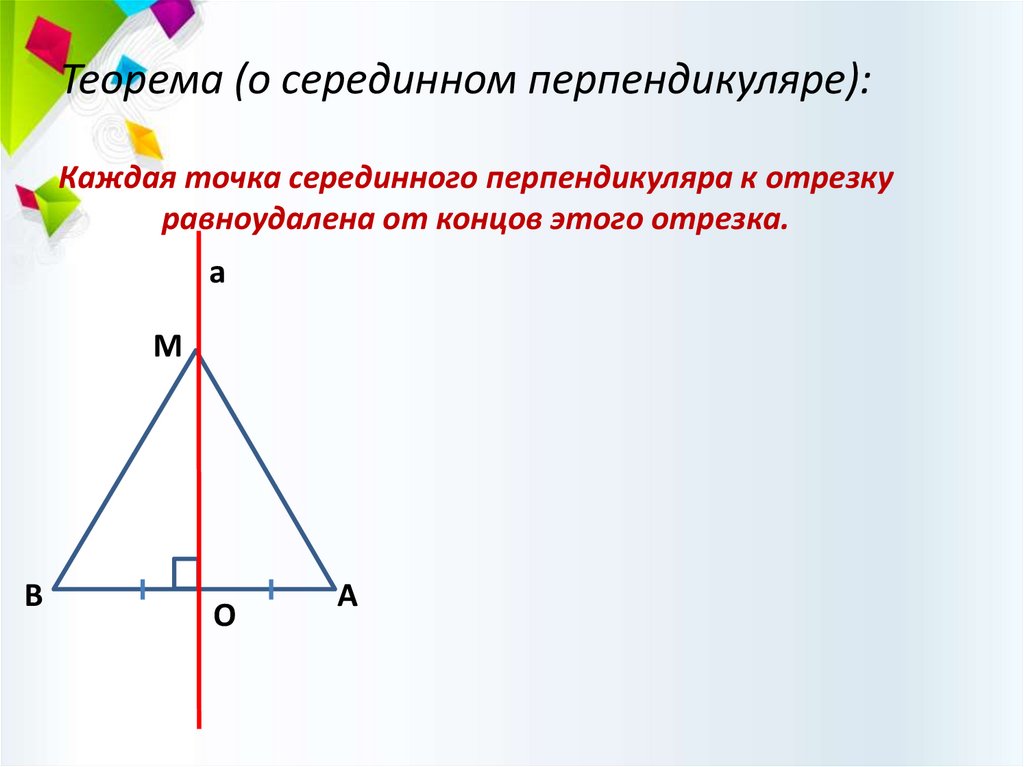
Теорема (о серединном перпендикуляре):Каждая точка серединного перпендикуляра к отрезку
равноудалена от концов этого отрезка.
a
М
B
O
А
48.
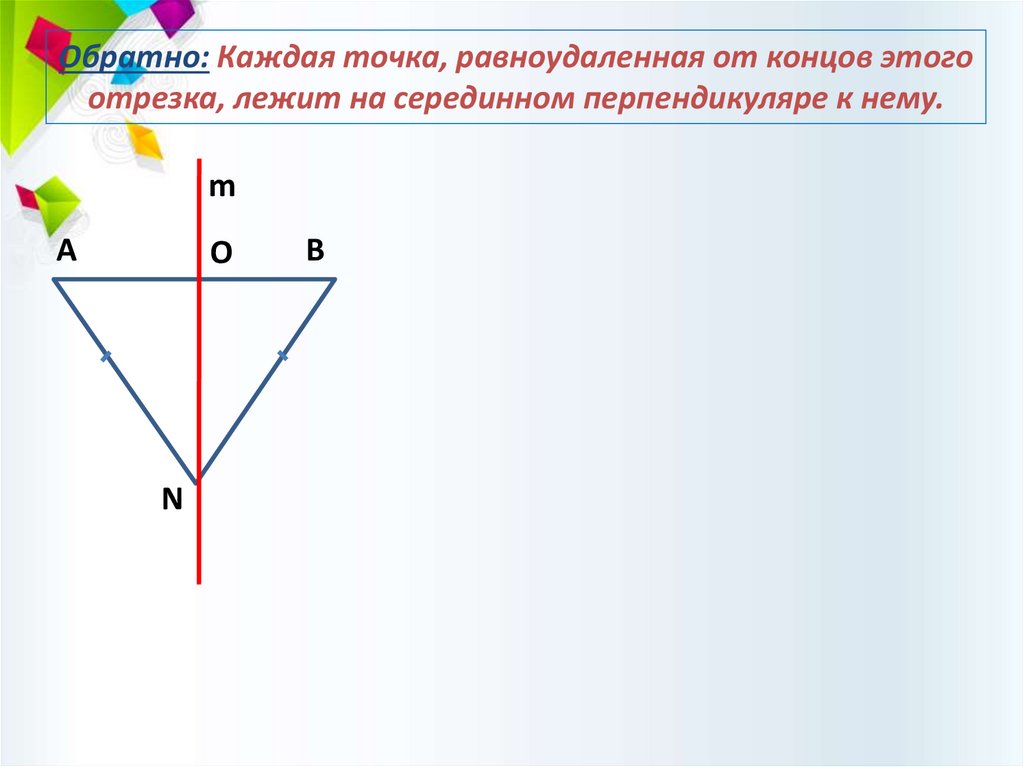
Обратно: Каждая точка, равноудаленная от концов этогоотрезка, лежит на серединном перпендикуляре к нему.
m
O
А
N
B
49.
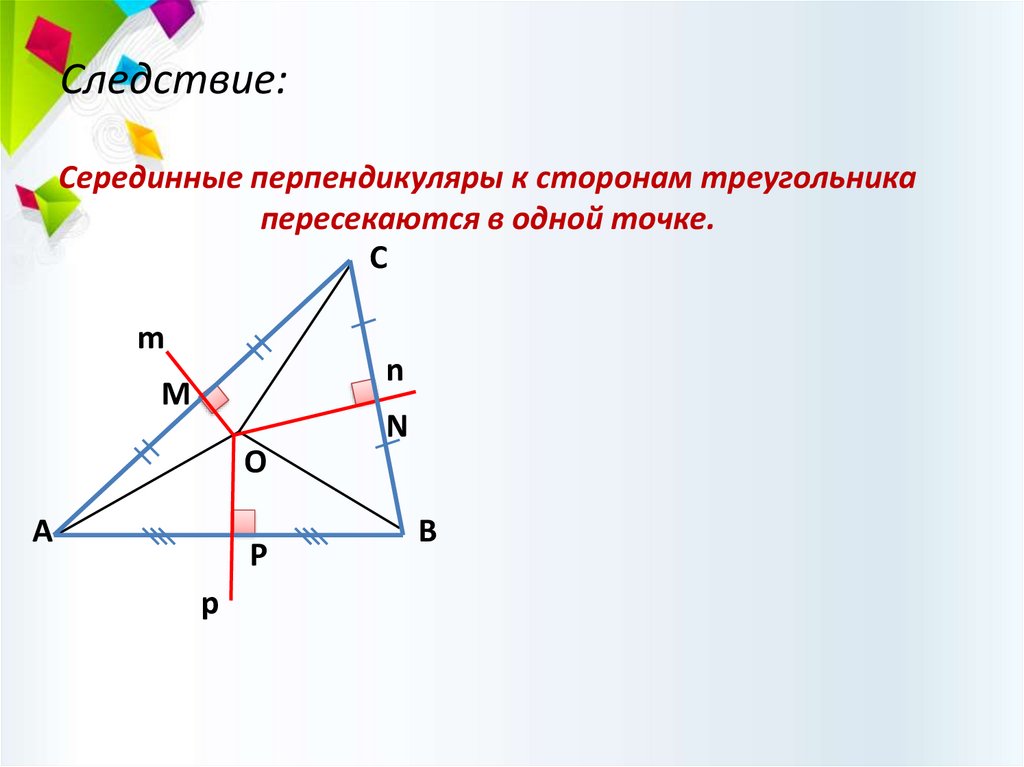
Следствие:Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
С
m
n
М
N
О
А
P
p
В
50.
Высоты треугольника(или их продолжения)
пересекаются в одной
точке.
51.
Вписанная окружность52.
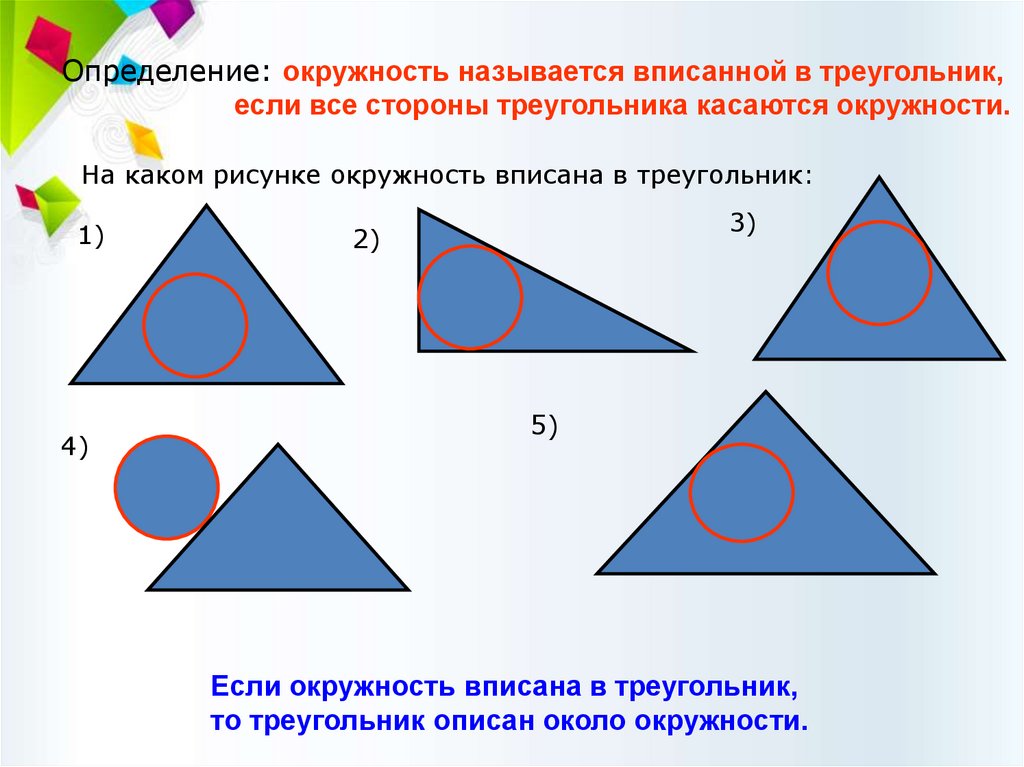
Определение: окружность называется вписанной в треугольник,если все стороны треугольника касаются окружности.
На каком рисунке окружность вписана в треугольник:
1)
4)
3)
2)
5)
Если окружность вписана в треугольник,
то треугольник описан около окружности.
53.
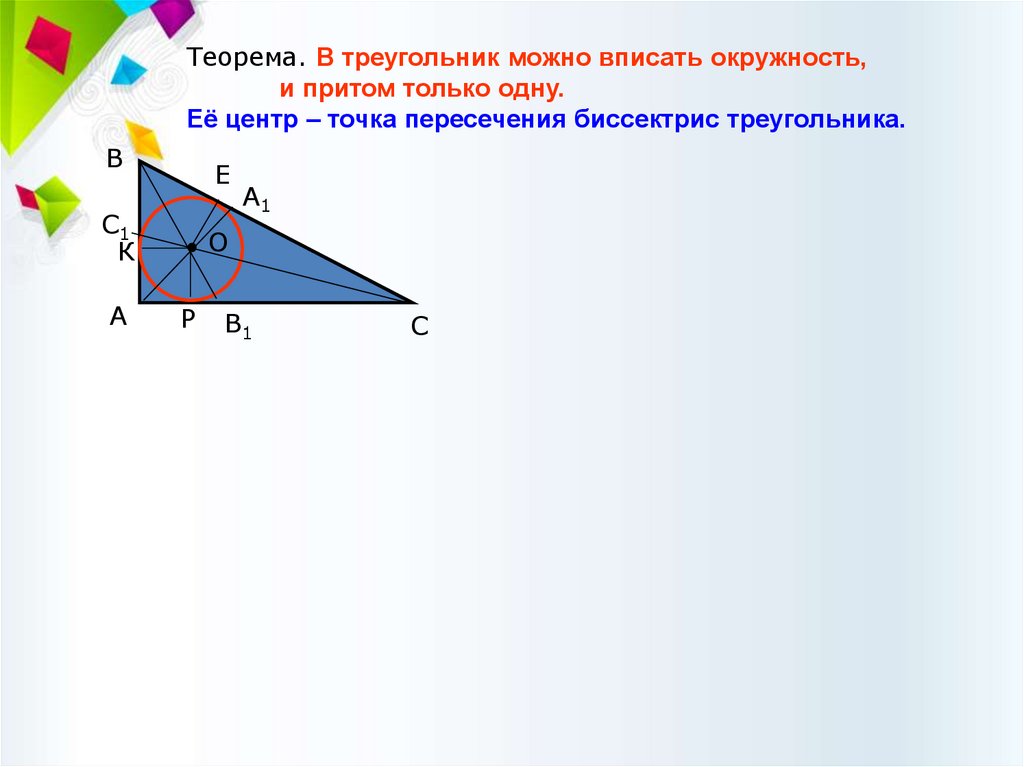
Теорема. В треугольник можно вписать окружность,и притом только одну.
Её центр – точка пересечения биссектрис треугольника.
В
Е
С1
К
А
А1
О
Р
В1
С
54.
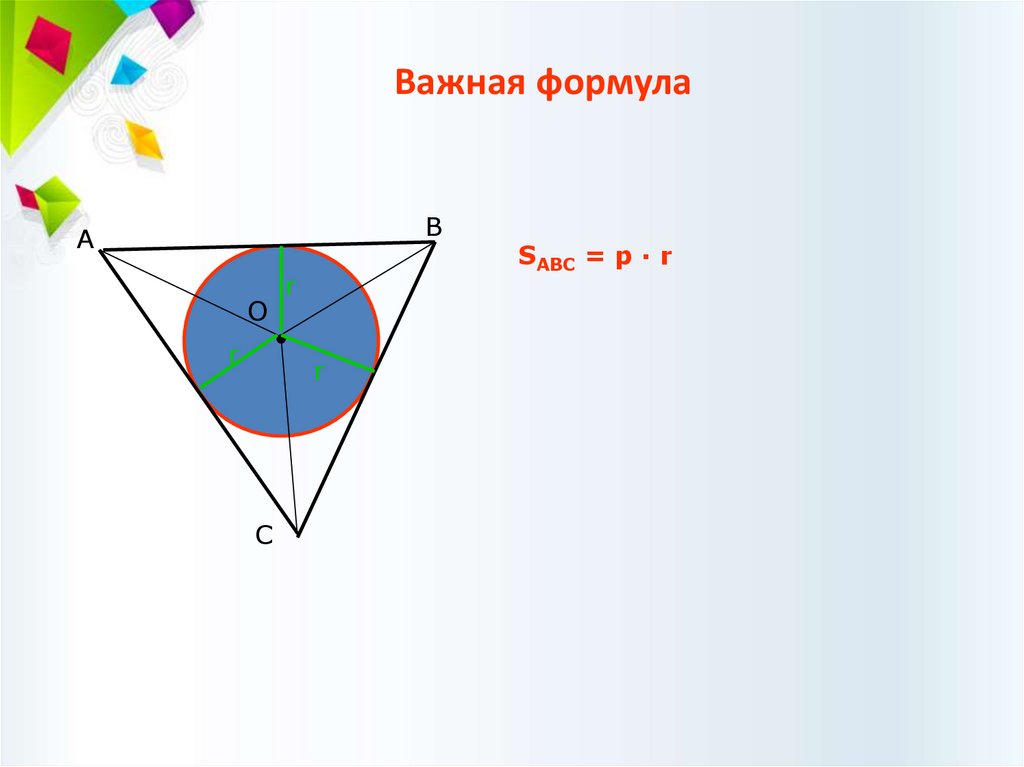
Важная формулаВ
А
О
r
r
r
С
SABC = p · r
55.
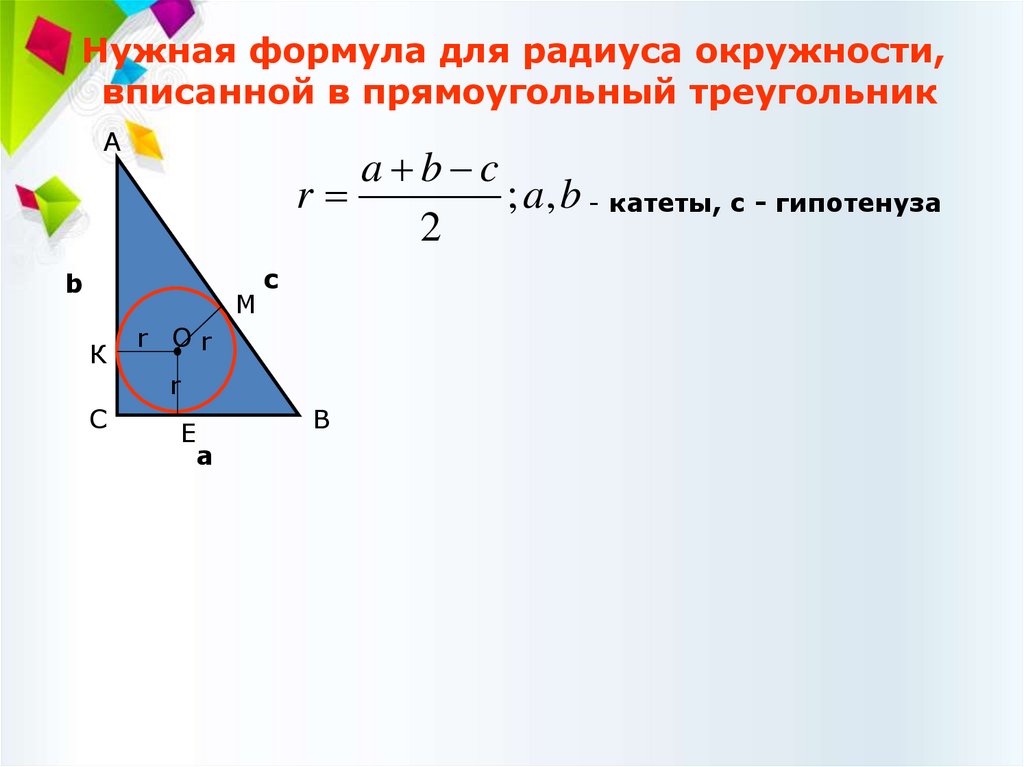
Нужная формула для радиуса окружности,вписанной в прямоугольный треугольник
А
a b c
r
; a, b - катеты, с - гипотенуза
2
b
М
К
С
c
r Оr
r
Е
a
В
56.
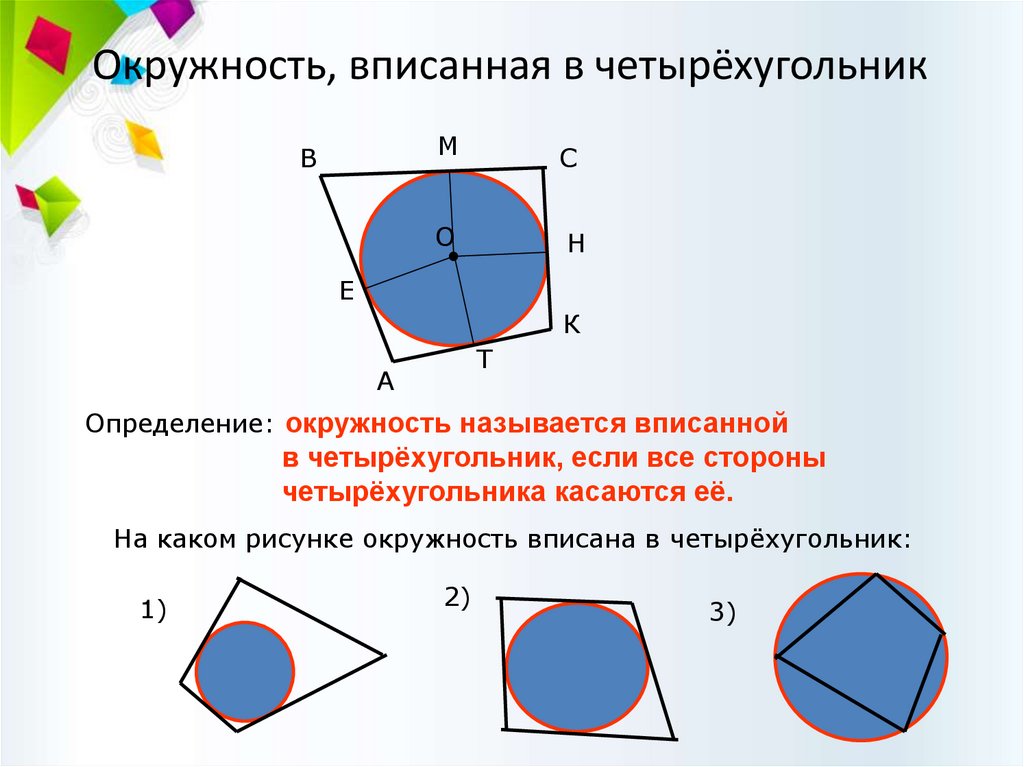
Окружность, вписанная в четырёхугольникМ
В
С
О
Н
Е
К
Т
А
Определение: окружность называется вписанной
в четырёхугольник, если все стороны
четырёхугольника касаются её.
На каком рисунке окружность вписана в четырёхугольник:
1)
2)
3)
57.
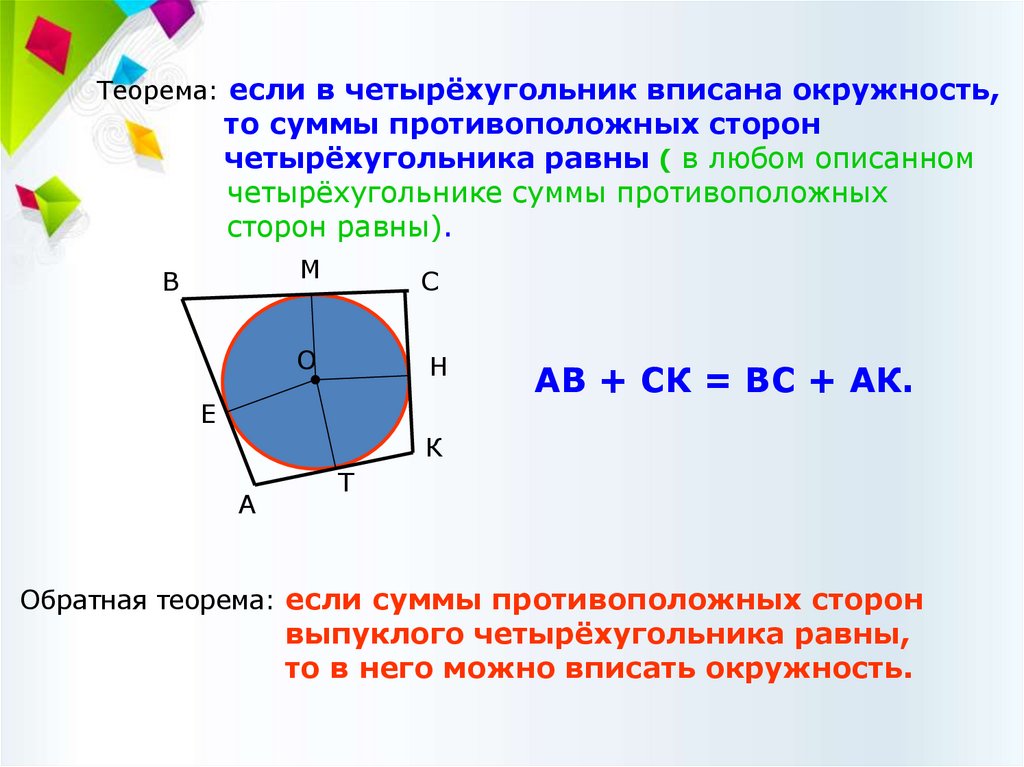
Теорема: если в четырёхугольник вписана окружность,то суммы противоположных сторон
четырёхугольника равны ( в любом описанном
четырёхугольнике суммы противоположных
сторон равны).
М
В
С
О
Н
Е
АВ + СК = ВС + АК.
К
А
Т
Обратная теорема: если суммы противоположных сторон
выпуклого четырёхугольника равны,
то в него можно вписать окружность.
58.
Описанная окружность59.
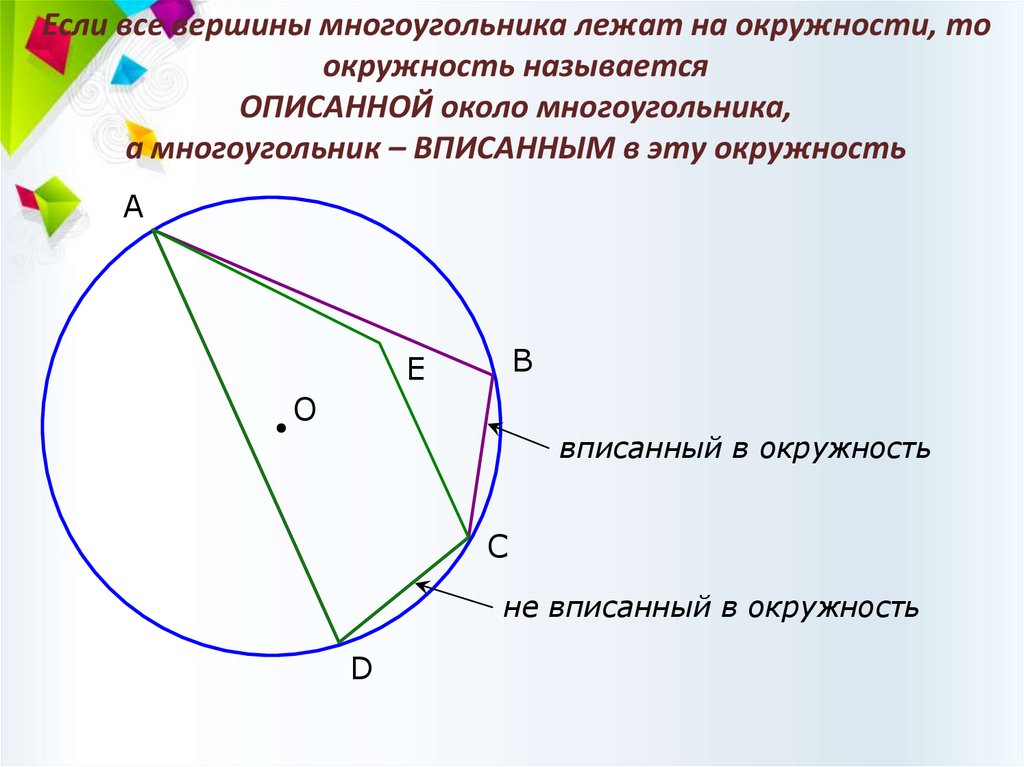
Если все вершины многоугольника лежат на окружности, тоокружность называется
ОПИСАННОЙ около многоугольника,
а многоугольник – ВПИСАННЫМ в эту окружность
A
B
E
O
вписанный в окружность
C
не вписанный в окружность
D
60.
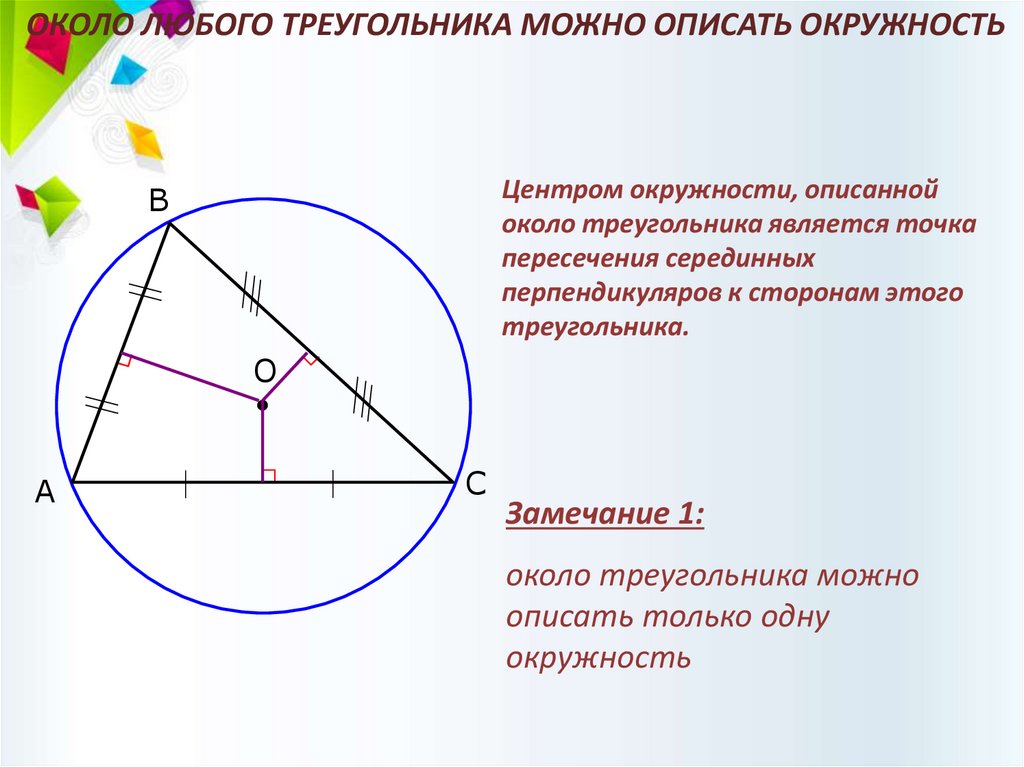
ОКОЛО ЛЮБОГО ТРЕУГОЛЬНИКА МОЖНО ОПИСАТЬ ОКРУЖНОСТЬЦентром окружности, описанной
около треугольника является точка
пересечения серединных
перпендикуляров к сторонам этого
треугольника.
В
О
А
С
Замечание 1:
около треугольника можно
описать только одну
окружность
61.
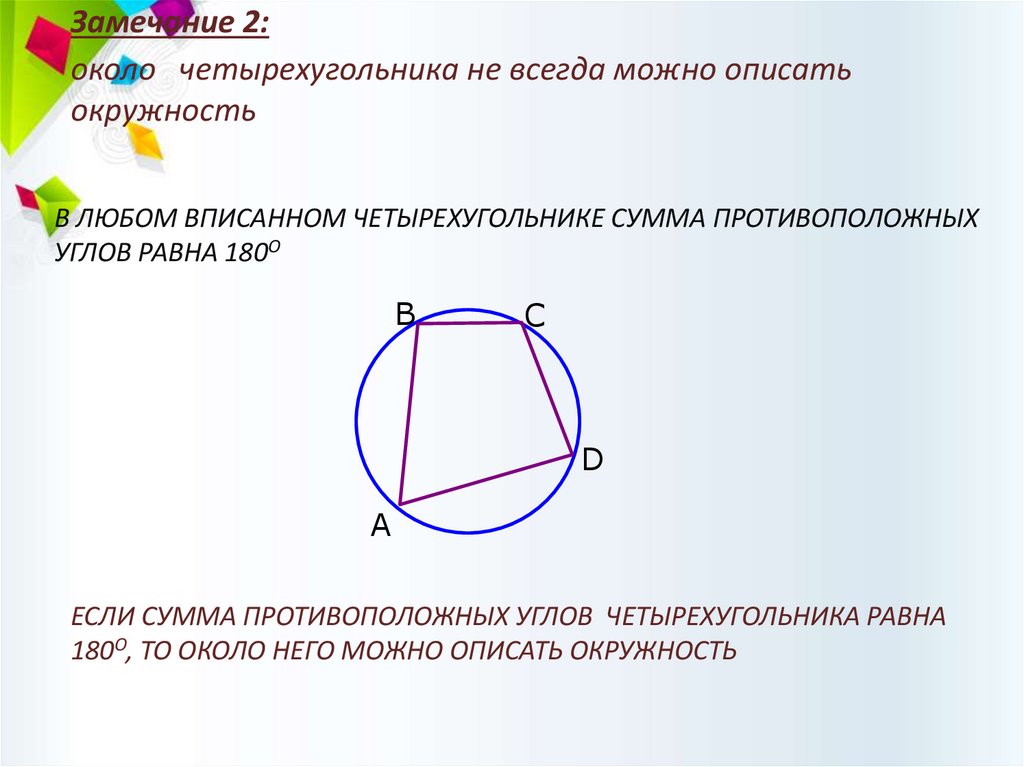
Замечание 2:около четырехугольника не всегда можно описать
окружность
В ЛЮБОМ ВПИСАННОМ ЧЕТЫРЕХУГОЛЬНИКЕ СУММА ПРОТИВОПОЛОЖНЫХ
УГЛОВ РАВНА 180О
B
C
D
A
ЕСЛИ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ ЧЕТЫРЕХУГОЛЬНИКА РАВНА
180О, ТО ОКОЛО НЕГО МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ
62.
Геометрия, 7 – 9 классы: учеб. для общеобразоват.
организаций / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и
др.] – 6-е изд. – М.: Просвещение, 2016.
Изучение геометрии в 7 – 9 классах: Пособие для учителей /
Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. – 7-е изд. – М.:
Просвещение, 2009.
http://mathege.ru/or/ege/Main.html - материалы открытого
банка заданий ЕГЭ по математике .











 mathematics
mathematics








