Обобщающие таблицы по геометрии. Треугольники, четырехугольники,, окружность, площади фигур, векторы движения

1.

2.

3.

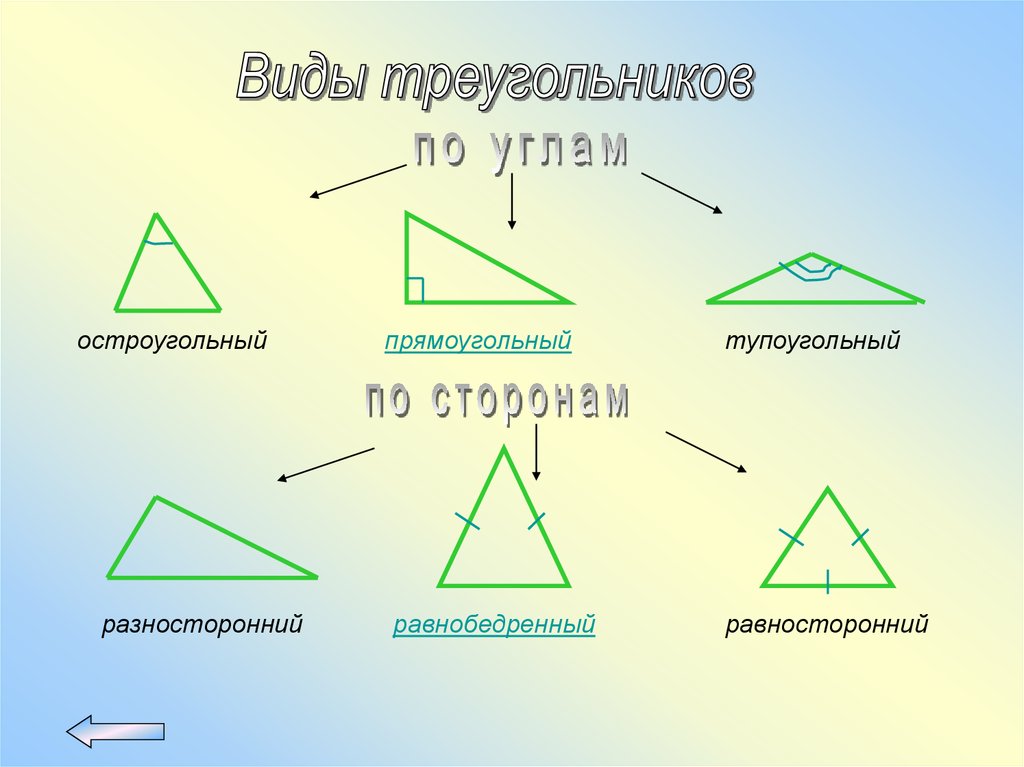
остроугольный
разносторонний
прямоугольный
равнобедренный
тупоугольный
равносторонний

4.

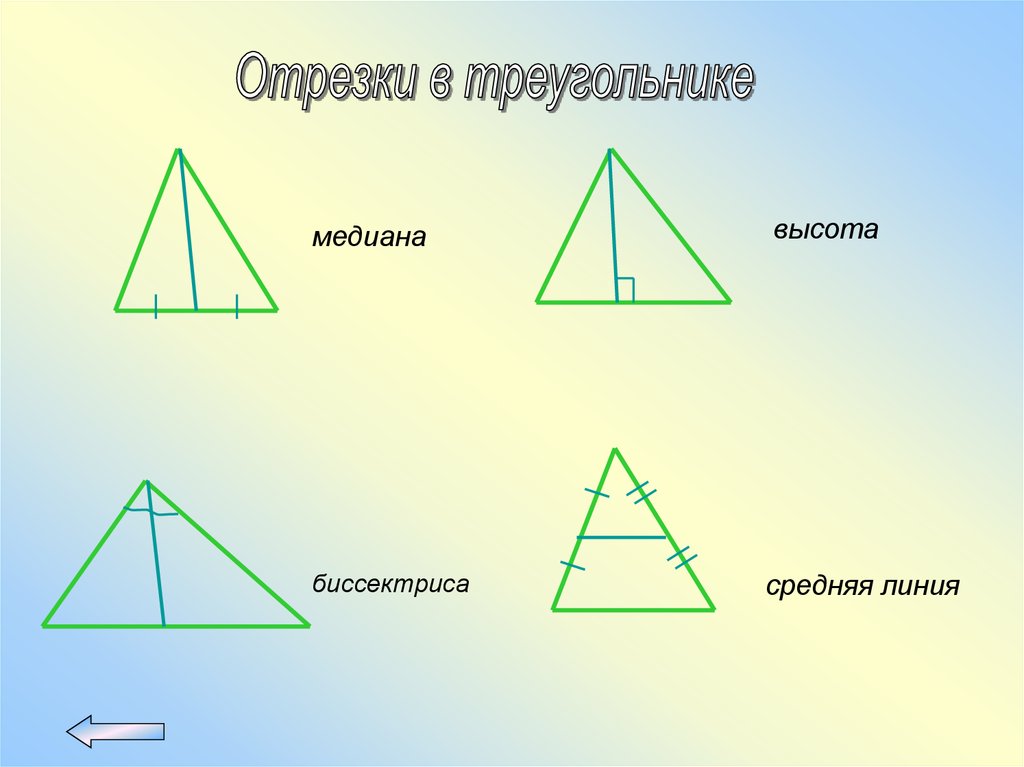
медиана
биссектриса
высота
средняя линия

5.

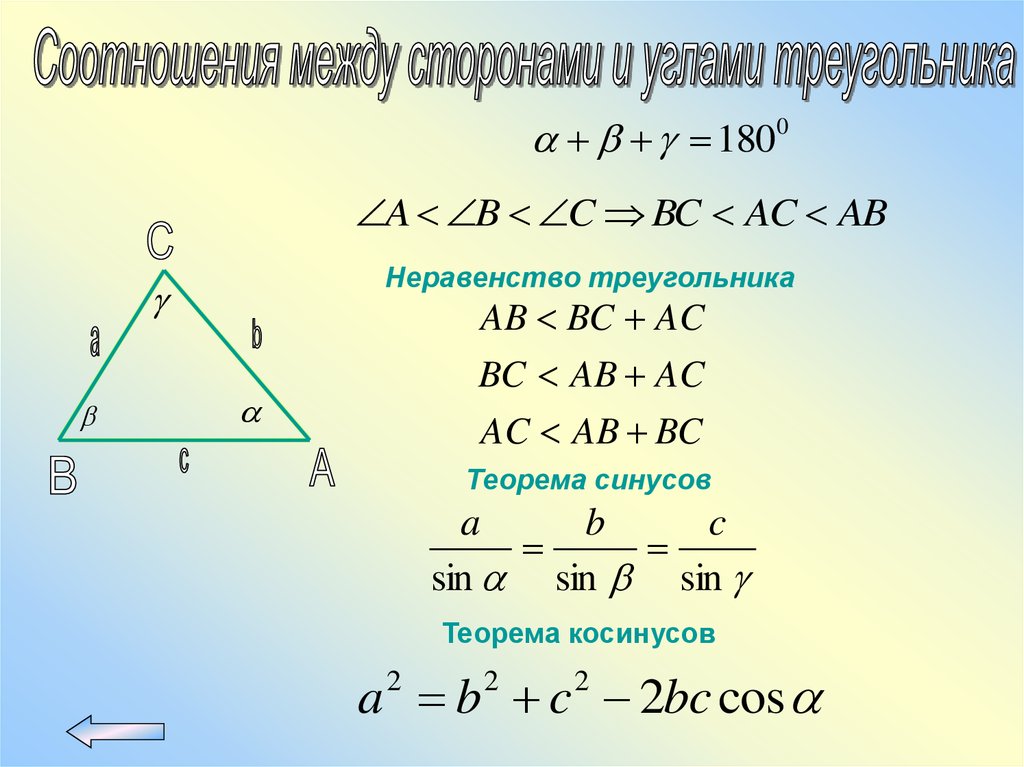
1800
A B C BC AC AB
Неравенство треугольника
AB BC AC
BC AB AC
AC AB BC
Теорема синусов
a
b
c
sin sin sin
Теорема косинусов
a b c 2bc cos
2
2
2

6.

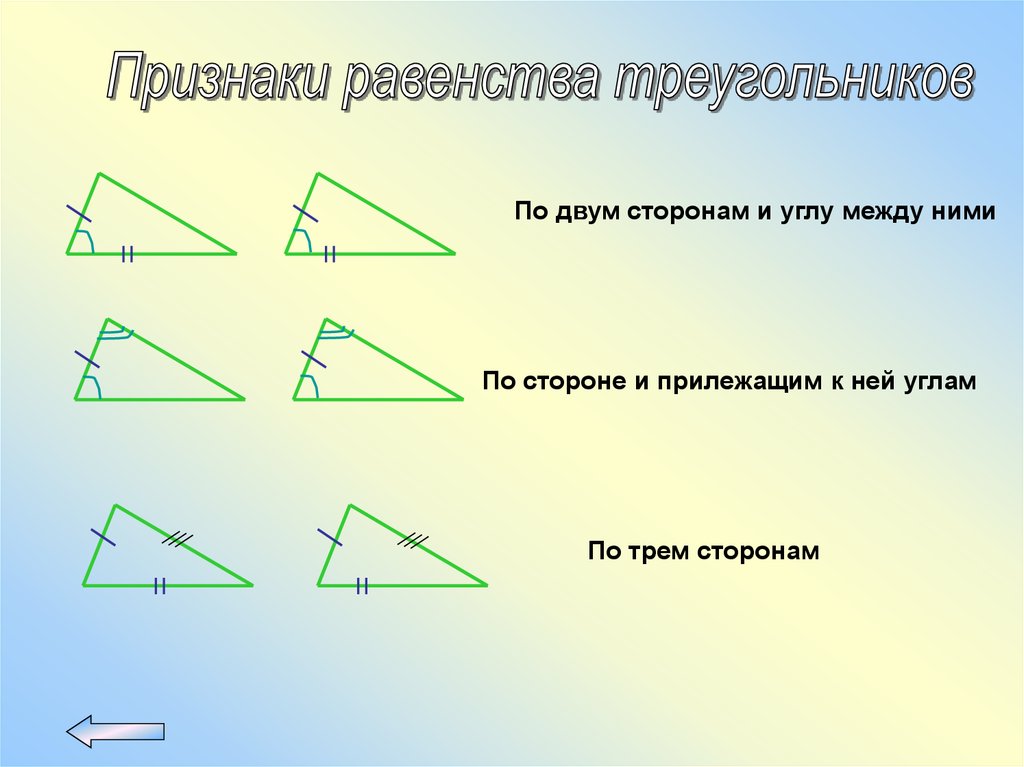
По двум сторонам и углу между ними
По стороне и прилежащим к ней углам
По трем сторонам

7.

8.

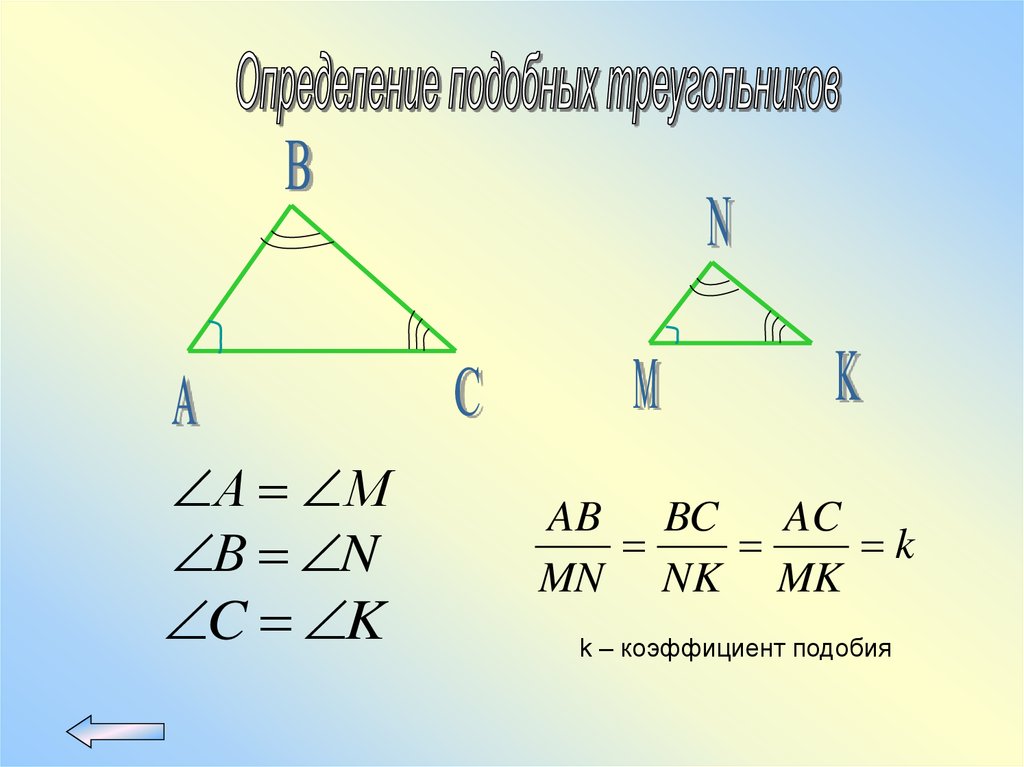
А М
В N
C K
AB BC
AC
k
MN NK MK
k – коэффициент подобия

9.

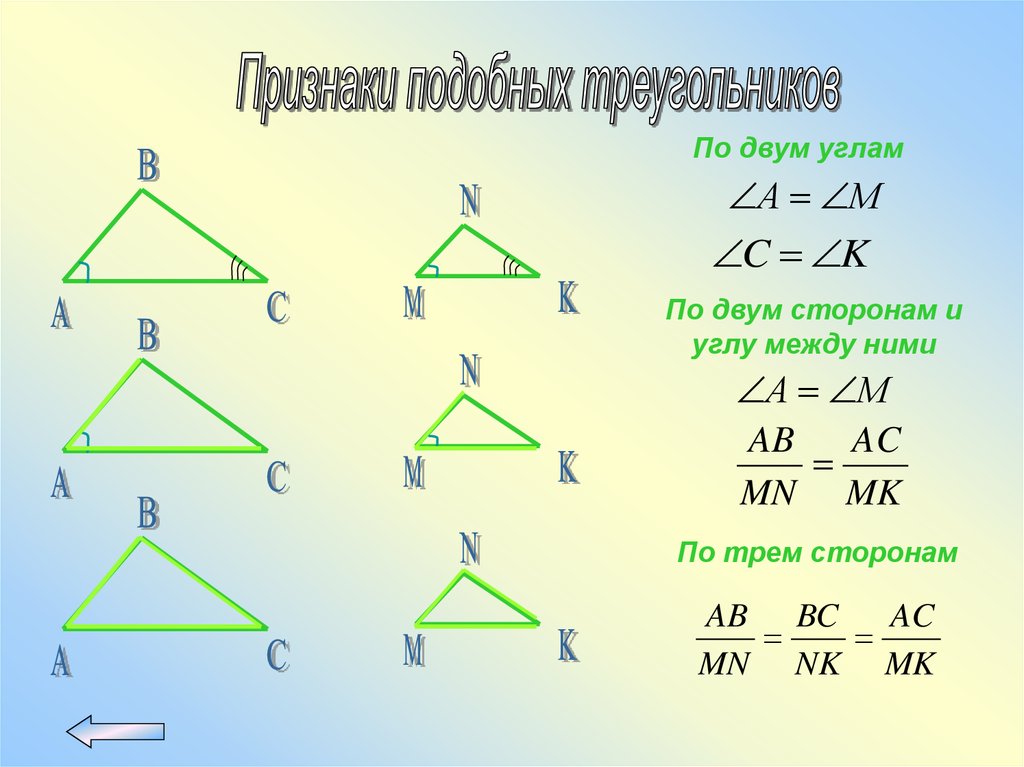
По двум углам
А М
C K
По двум сторонам и
углу между ними
А М
AB
AC
MN MK
По трем сторонам
AB BC
AC
MN NK MK

10.

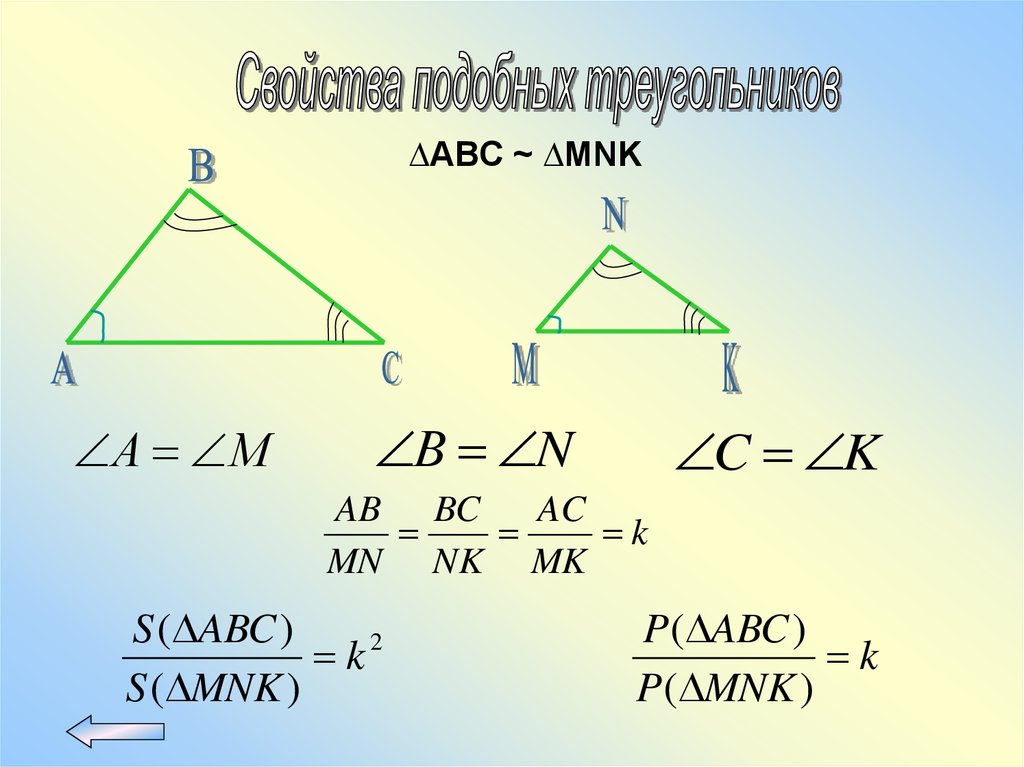
∆ABC ~ ∆MNK
А М
В N
C K
AB BC
AC
k
MN NK MK
S ( ABC )
k2
S ( MNK )
P( ABC )
k
P( MNK )

11.

12.

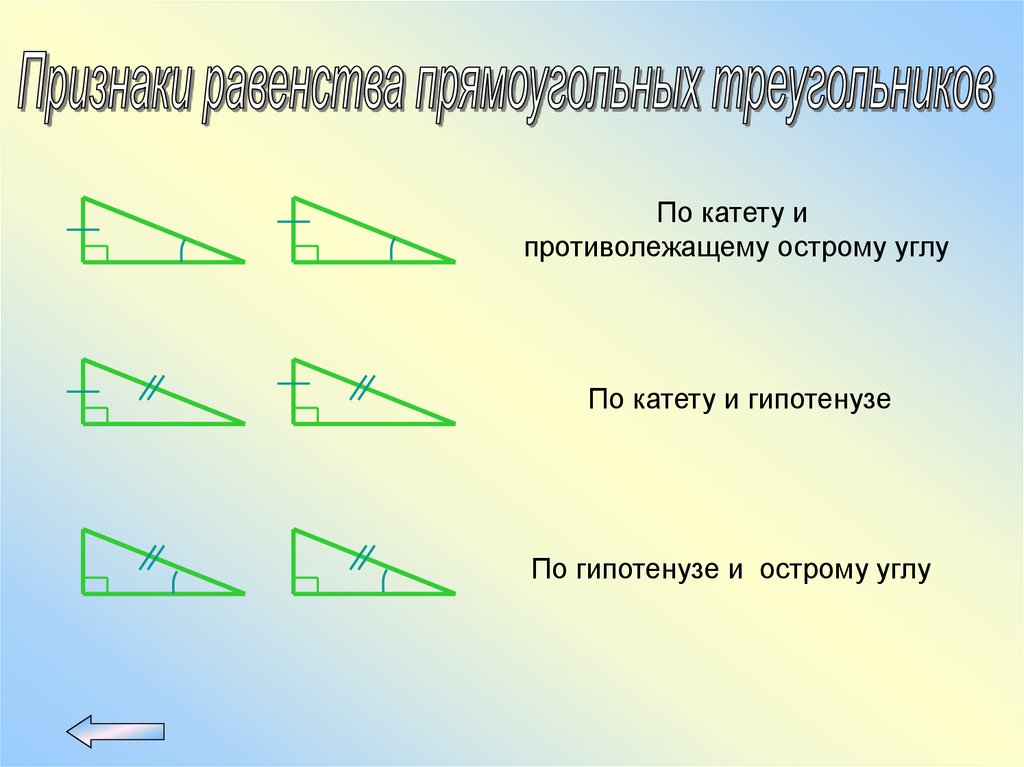
По катету и
противолежащему острому углу
По катету и гипотенузе
По гипотенузе и острому углу

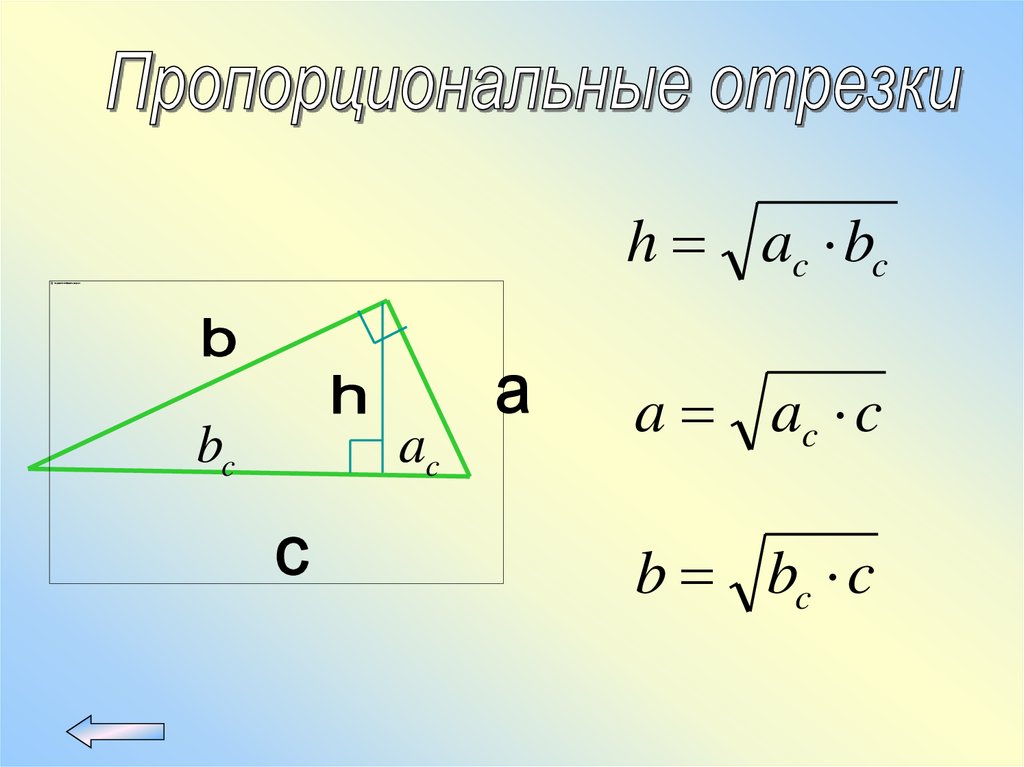
13.

h ac bc
bc
ac
a ac c
b bc c

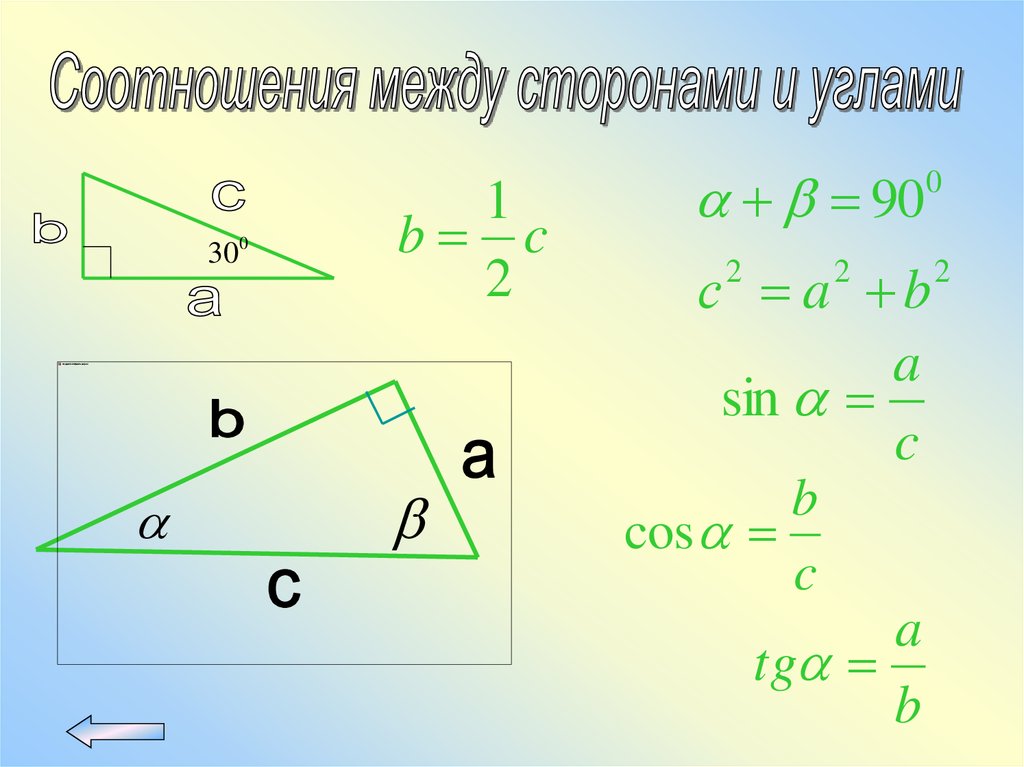
14.

300
1
b c
2
90
0
с a b
a
sin
c
2
2
b
cos
c
a
tg
b
2

15.

16.

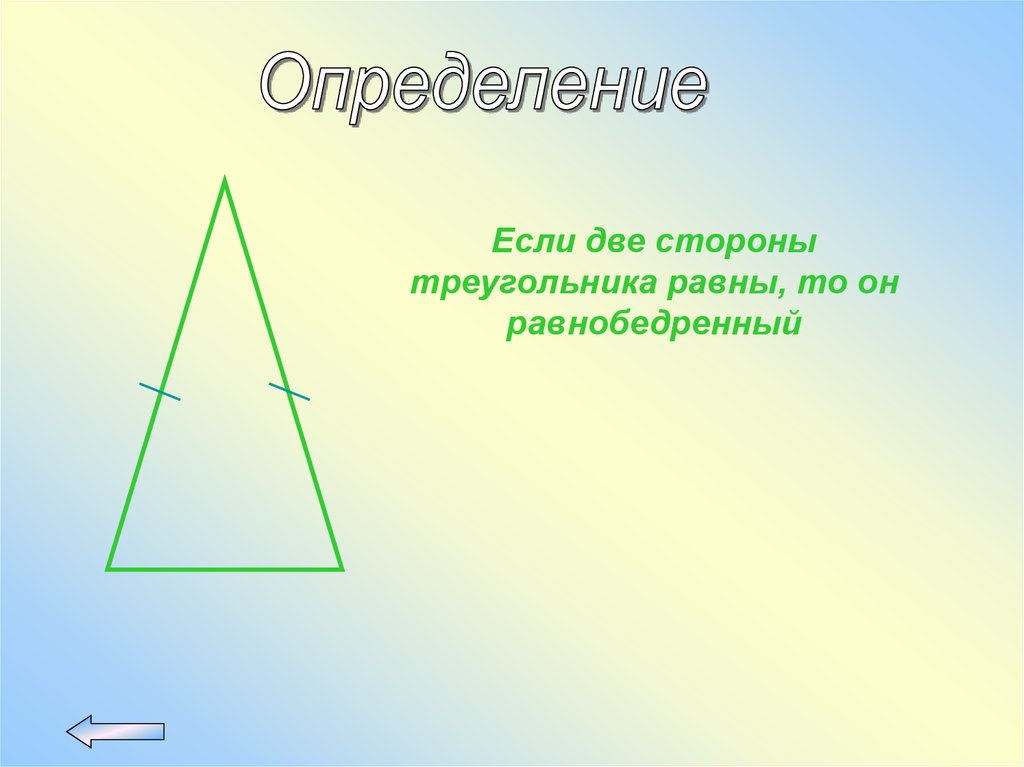
Если две стороны
треугольника равны, то он
равнобедренный

17.

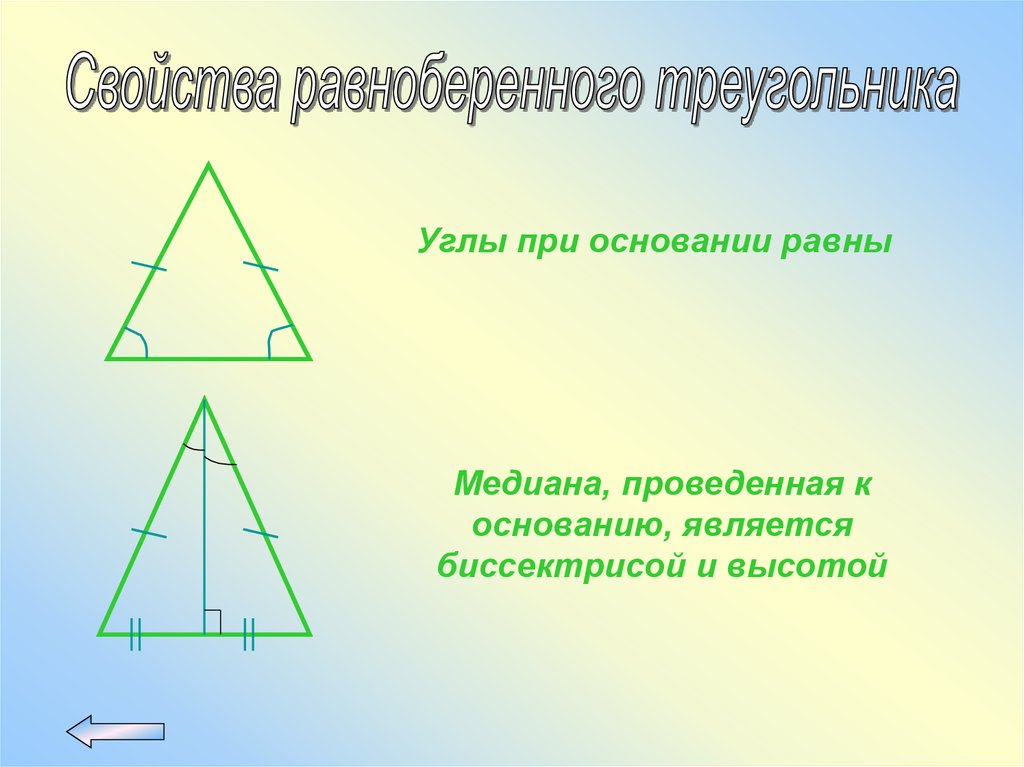
Углы при основании равны
Медиана, проведенная к
основанию, является
биссектрисой и высотой

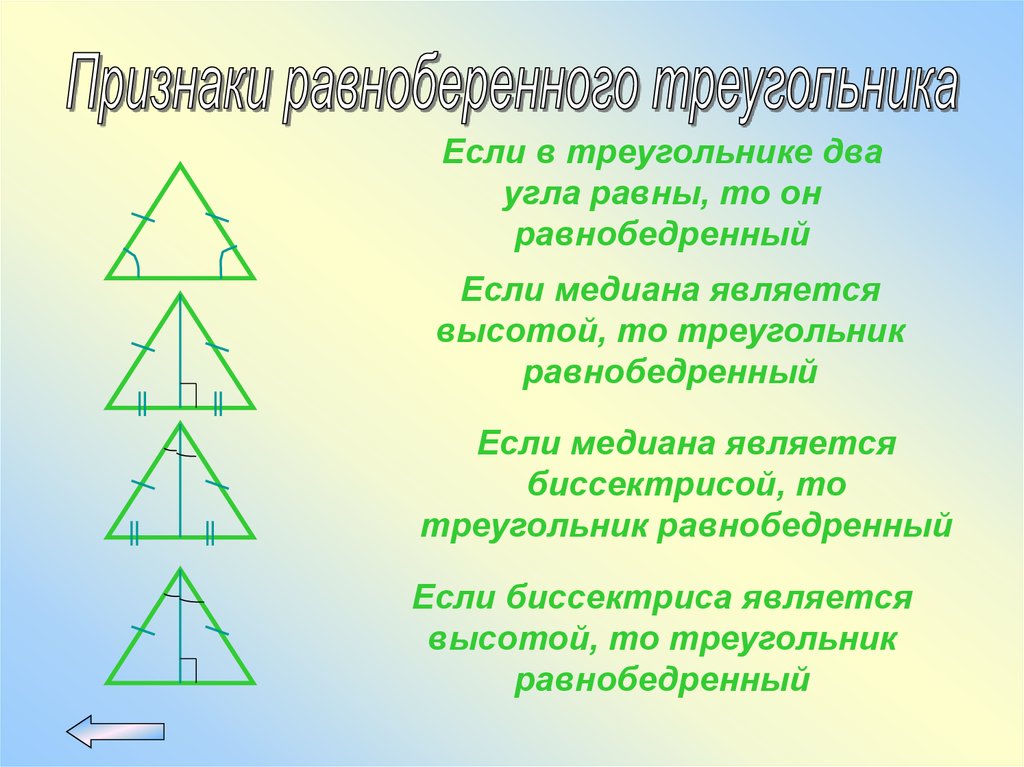
18.

Если в треугольнике два
угла равны, то он
равнобедренный
Если медиана является
высотой, то треугольник
равнобедренный
Если медиана является
биссектрисой, то
треугольник равнобедренный
Если биссектриса является
высотой, то треугольник
равнобедренный

19.

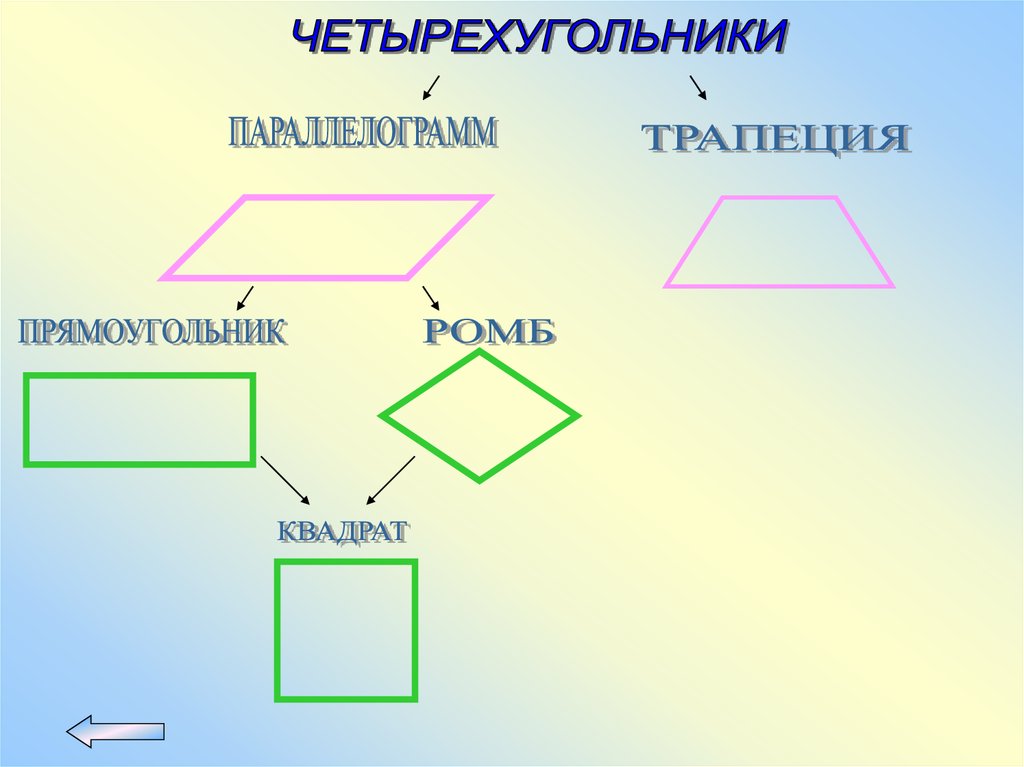
20.

21.

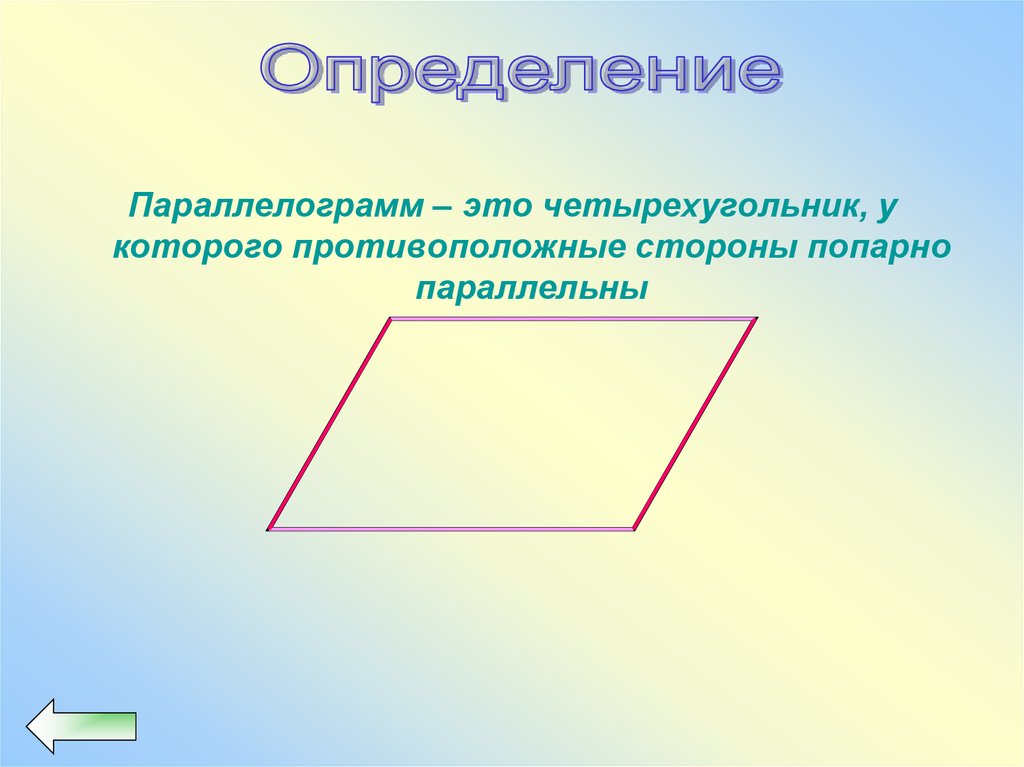
Параллелограмм – это четырехугольник, у
которого противоположные стороны попарно
параллельны

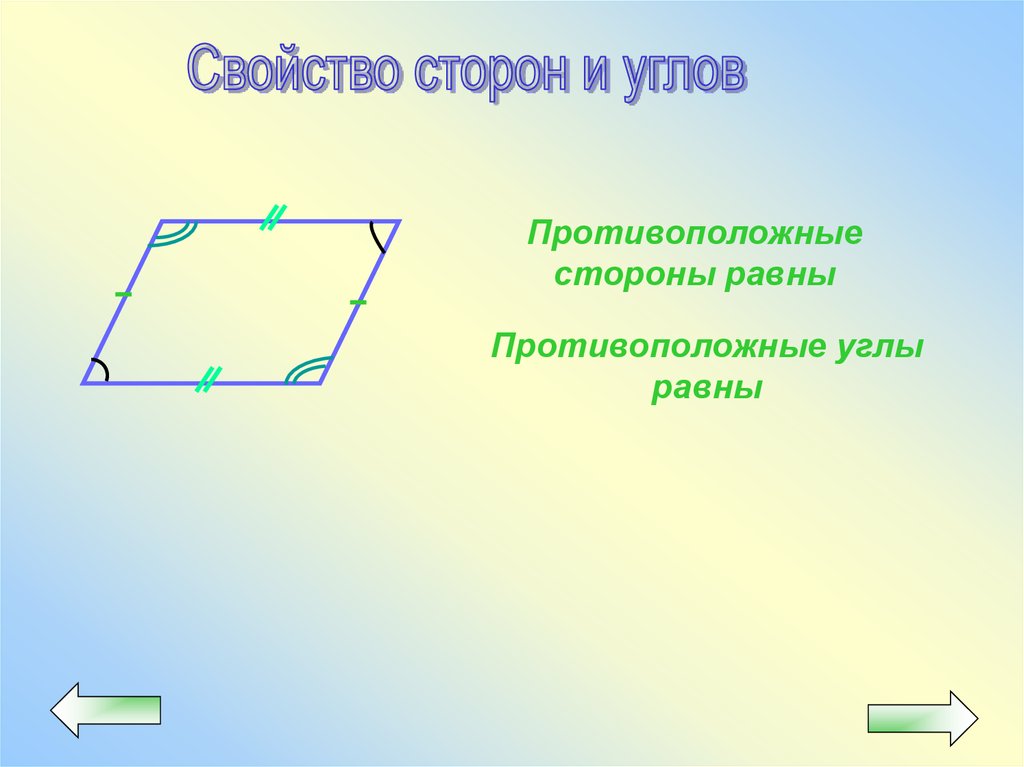
22.

Противоположные
стороны равны
Противоположные углы
равны

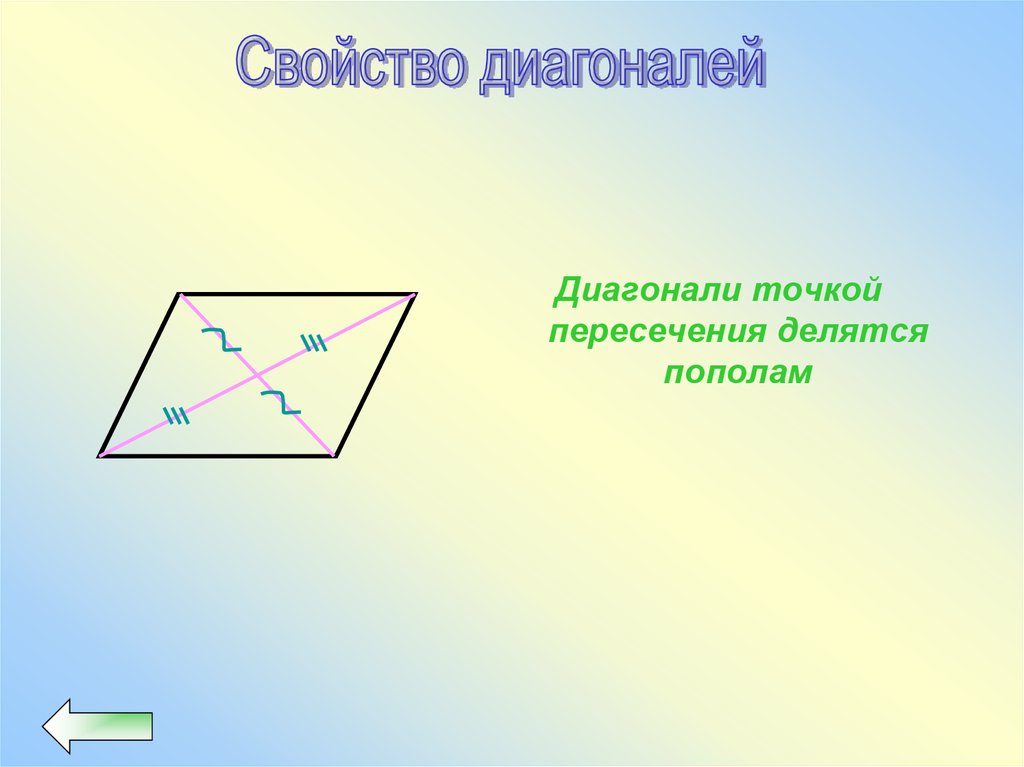
23.

Диагонали точкой
пересечения делятся
пополам

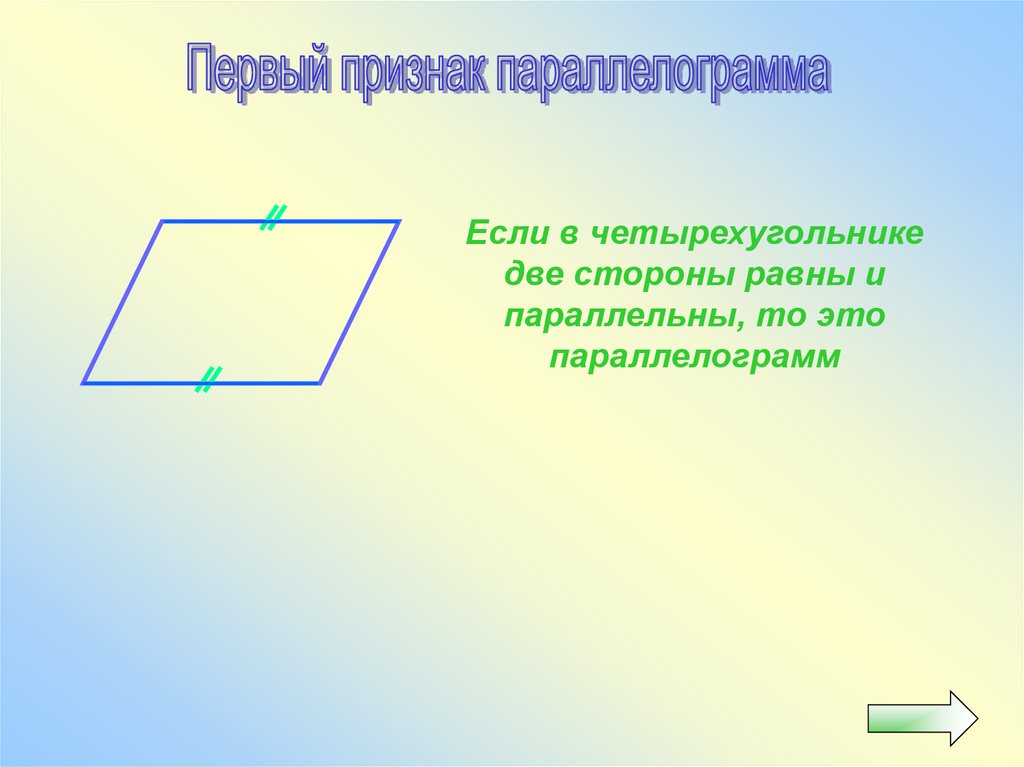
24.

Если в четырехугольнике
две стороны равны и
параллельны, то это
параллелограмм

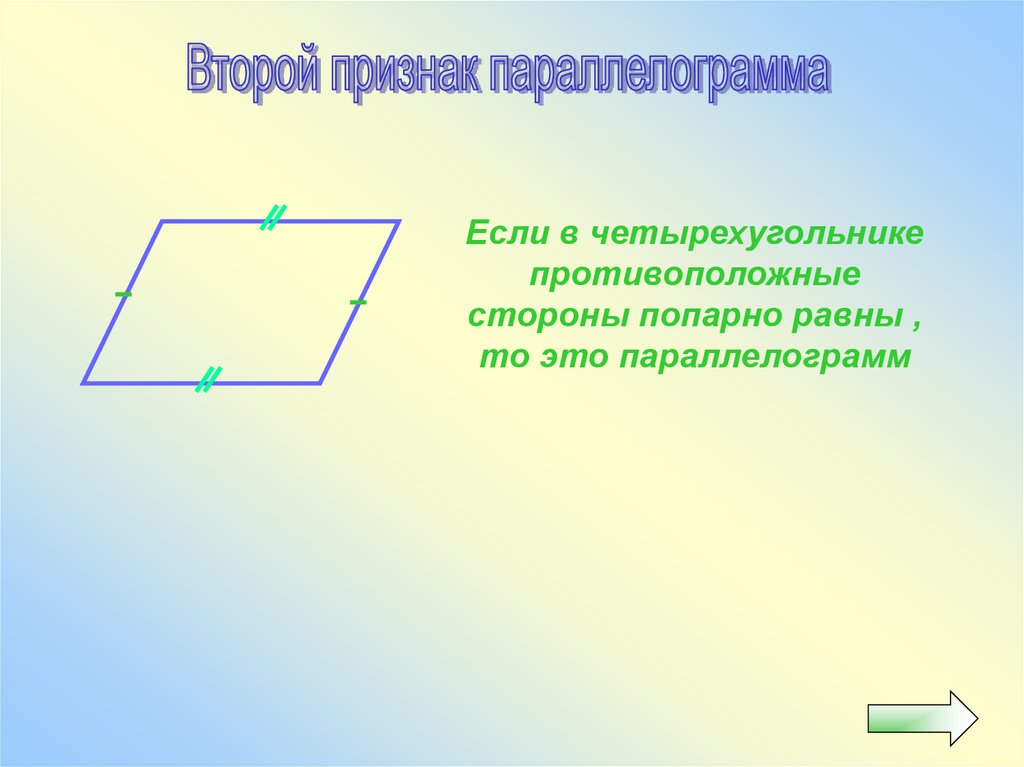
25.

Если в четырехугольнике
противоположные
стороны попарно равны ,
то это параллелограмм

26.

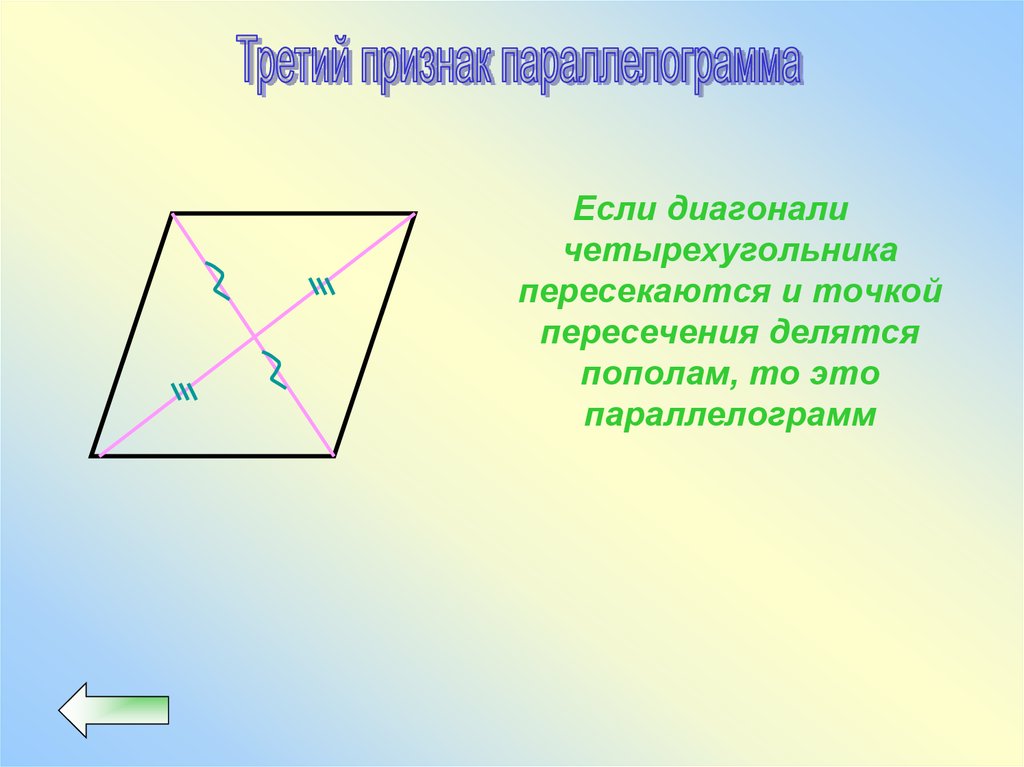
Если диагонали
четырехугольника
пересекаются и точкой
пересечения делятся
пополам, то это
параллелограмм

27.

28.

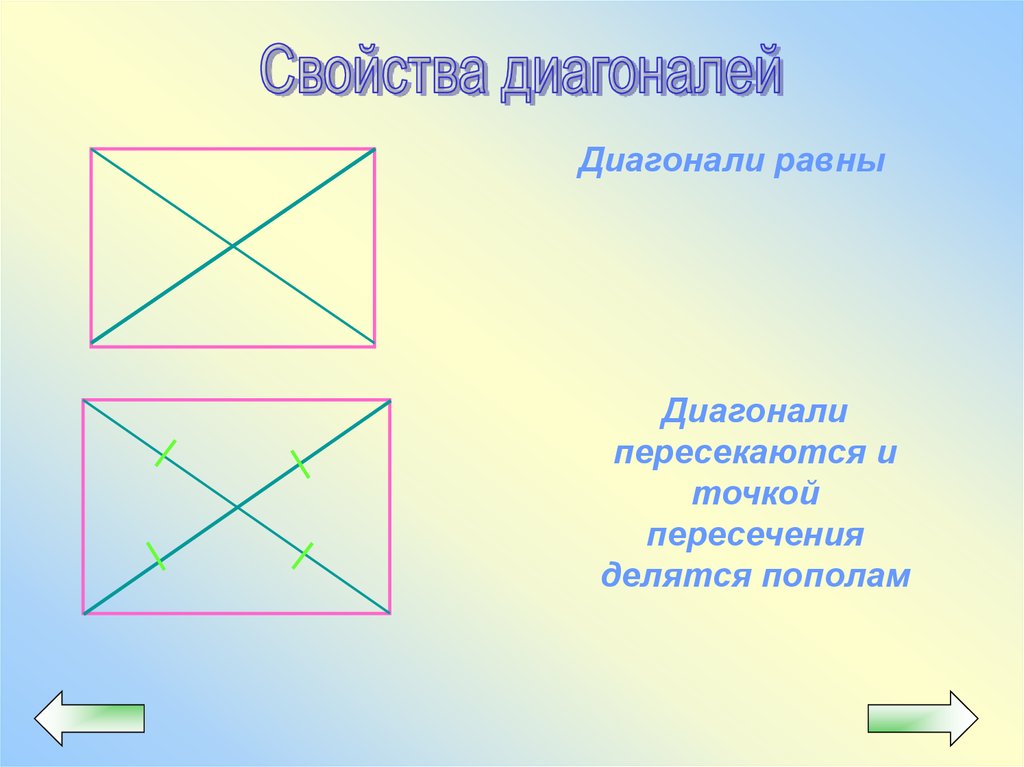
Диагонали равны
Диагонали
пересекаются и
точкой
пересечения
делятся пополам

29.

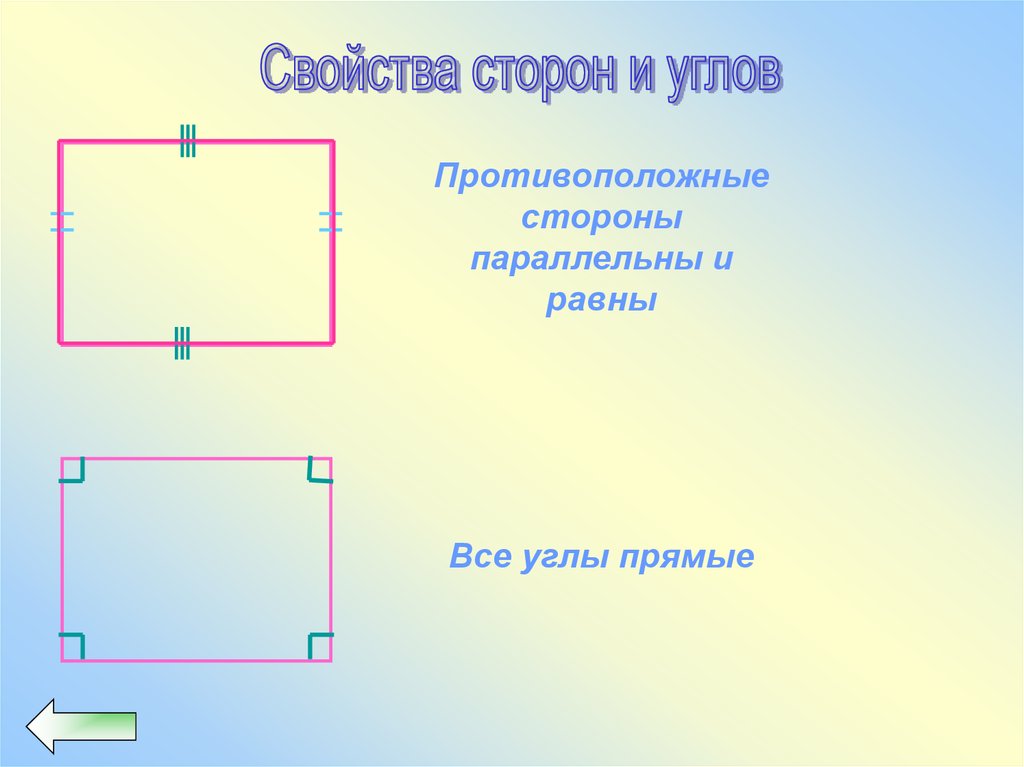
Противоположные
стороны
параллельны и
равны
Все углы прямые

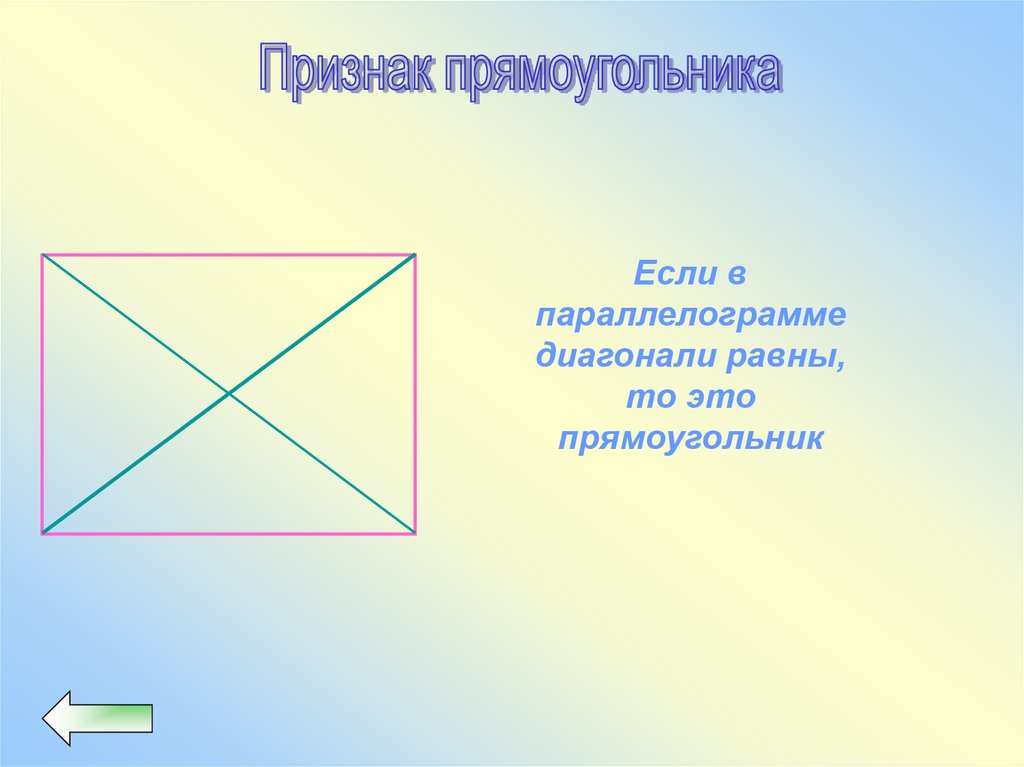
30.

Если в
параллелограмме
диагонали равны,
то это
прямоугольник

31.

32.

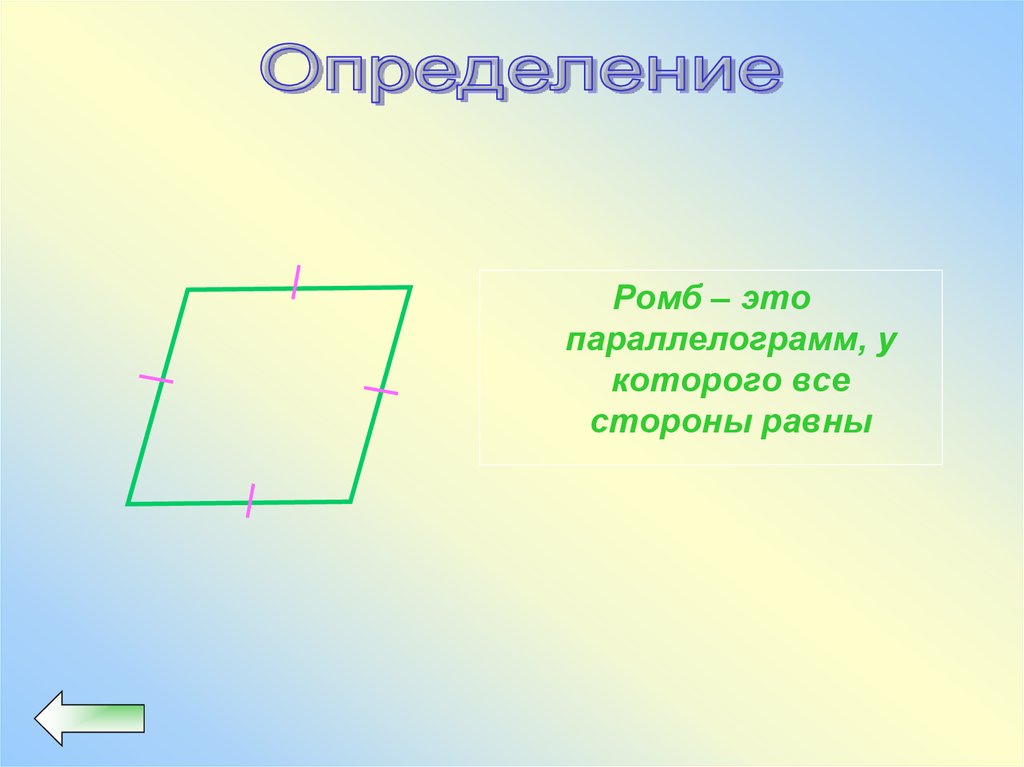
Ромб – это
параллелограмм, у
которого все
стороны равны

33.

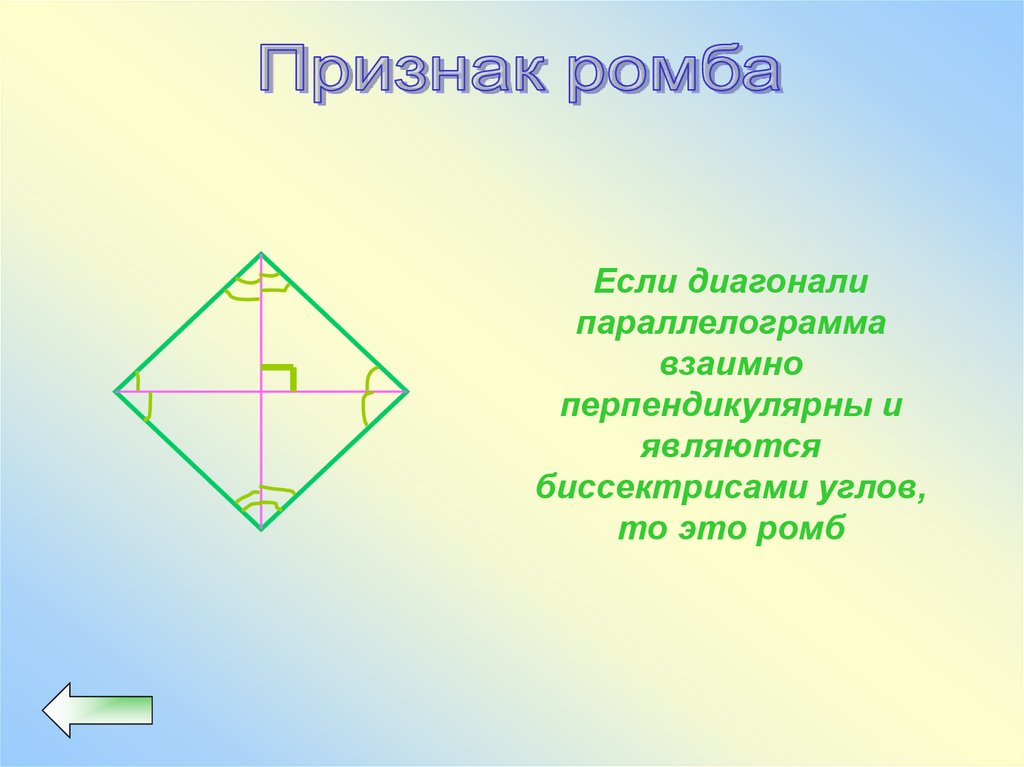
Если диагонали
параллелограмма
взаимно
перпендикулярны и
являются
биссектрисами углов,
то это ромб

34.

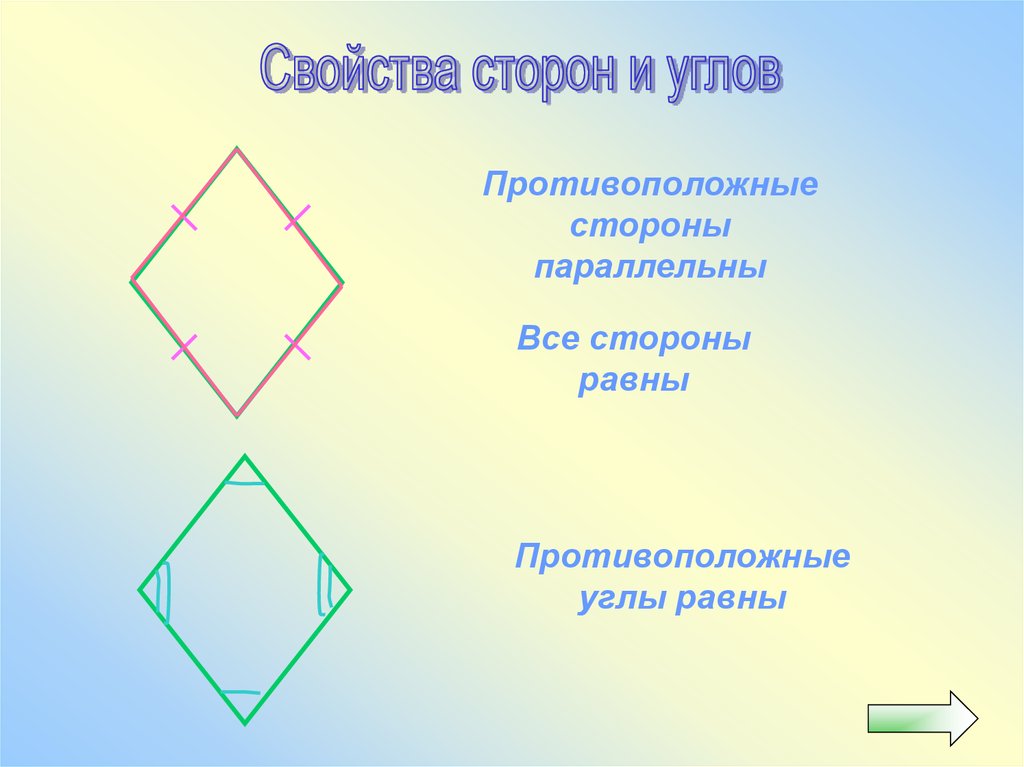
Противоположные
стороны
параллельны
Все стороны
равны
Противоположные
углы равны

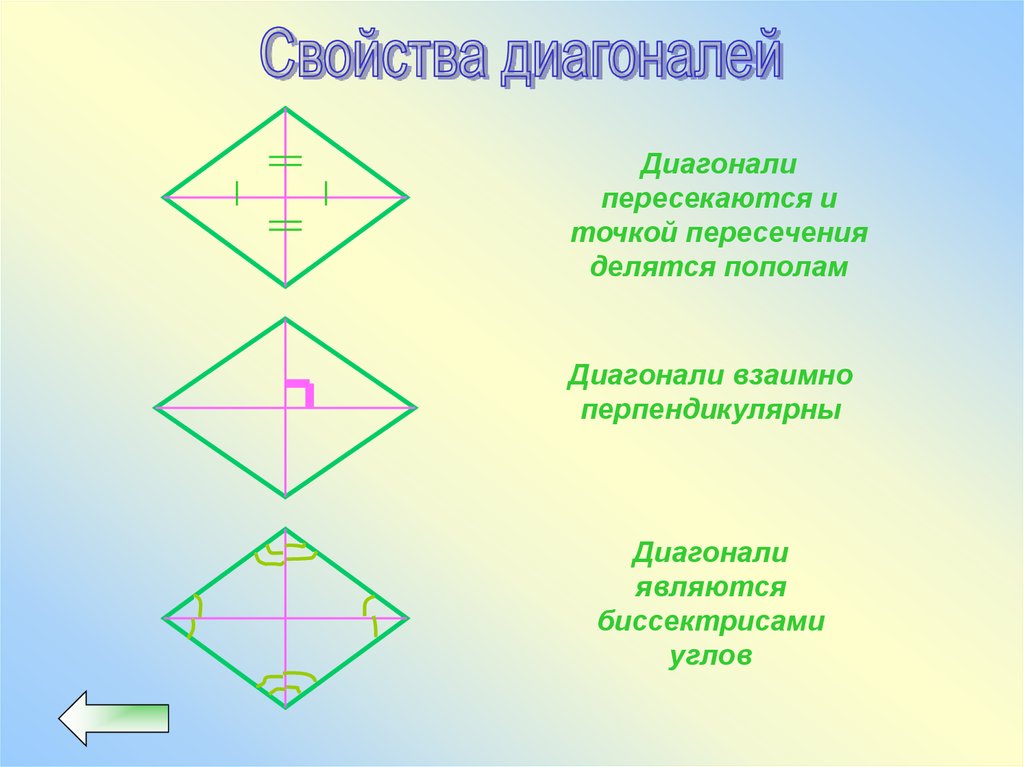
35.

Диагонали
пересекаются и
точкой пересечения
делятся пополам
Диагонали взаимно
перпендикулярны
Диагонали
являются
биссектрисами
углов

36.

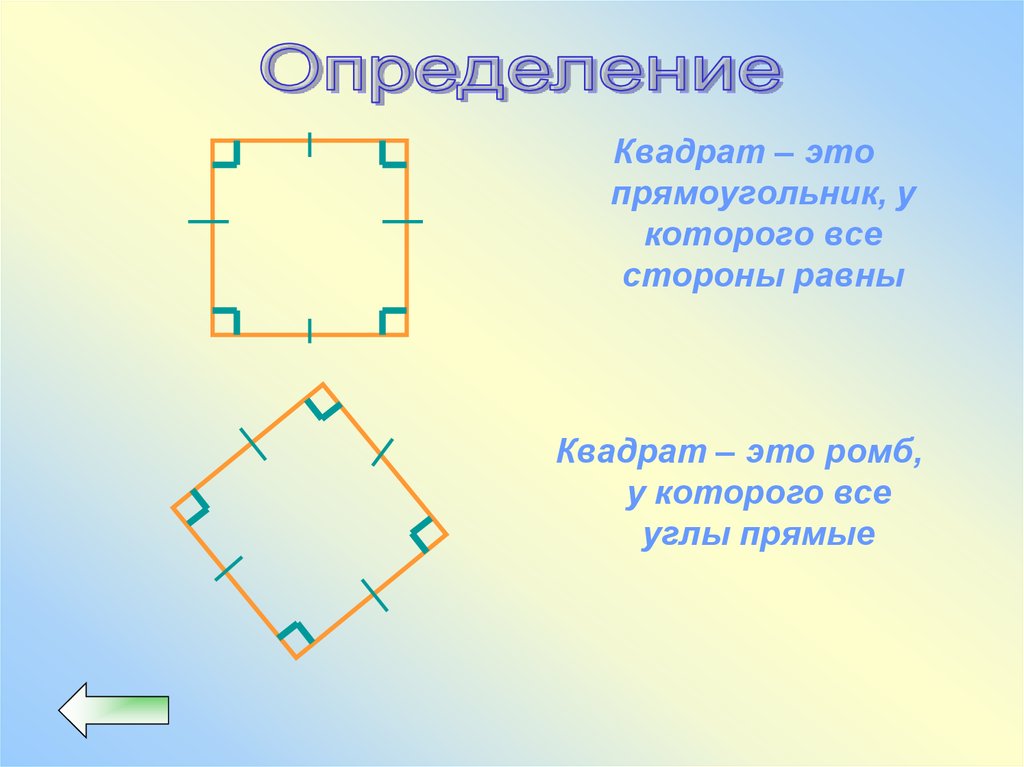
37.

Квадрат – это
прямоугольник, у
которого все
стороны равны
Квадрат – это ромб,
у которого все
углы прямые

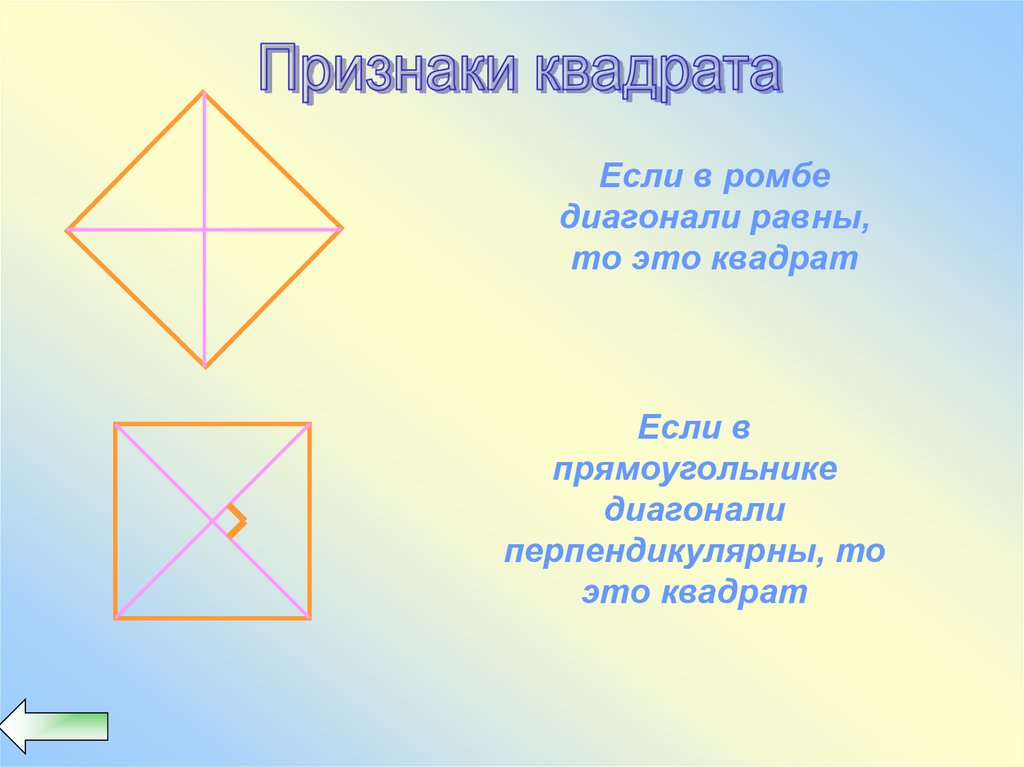
38.

Если в ромбе
диагонали равны,
то это квадрат
Если в
прямоугольнике
диагонали
перпендикулярны, то
это квадрат

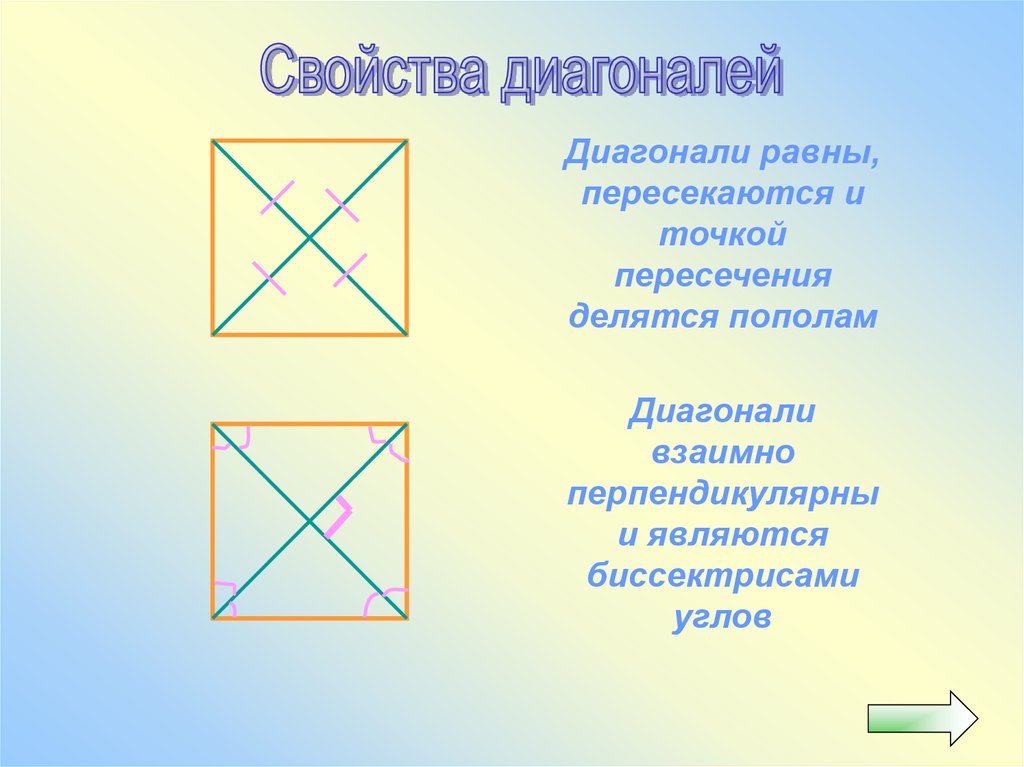
39.

Диагонали равны,
пересекаются и
точкой
пересечения
делятся пополам
Диагонали
взаимно
перпендикулярны
и являются
биссектрисами
углов

40.

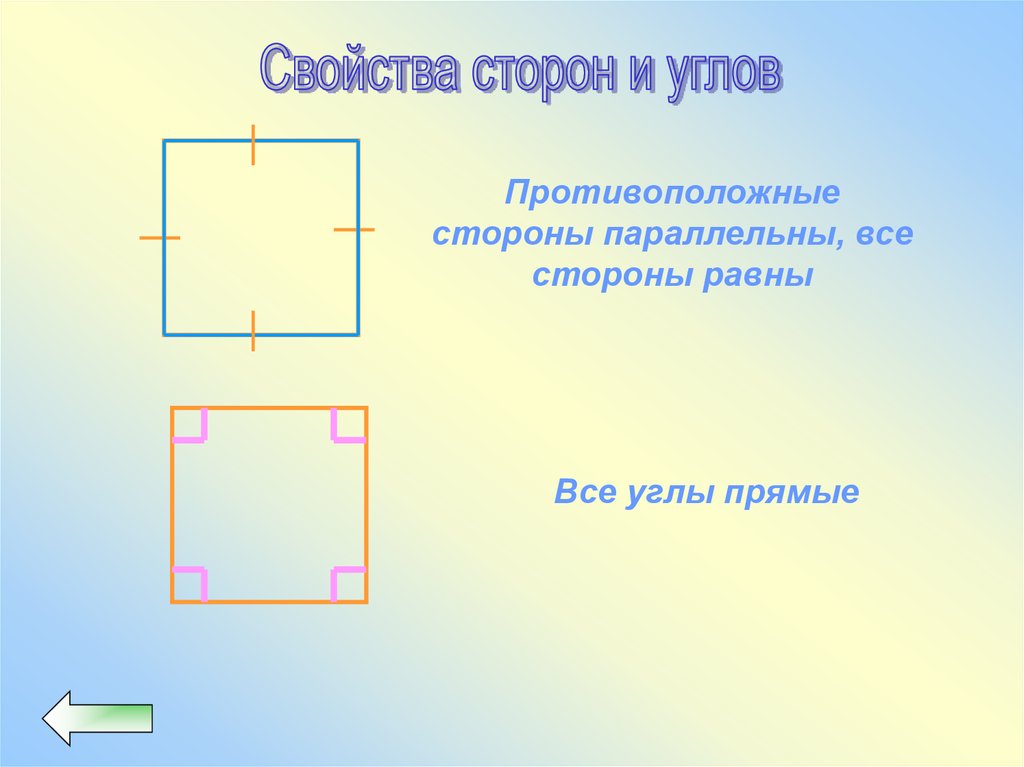
Противоположные
стороны параллельны, все
стороны равны
Все углы прямые

41.

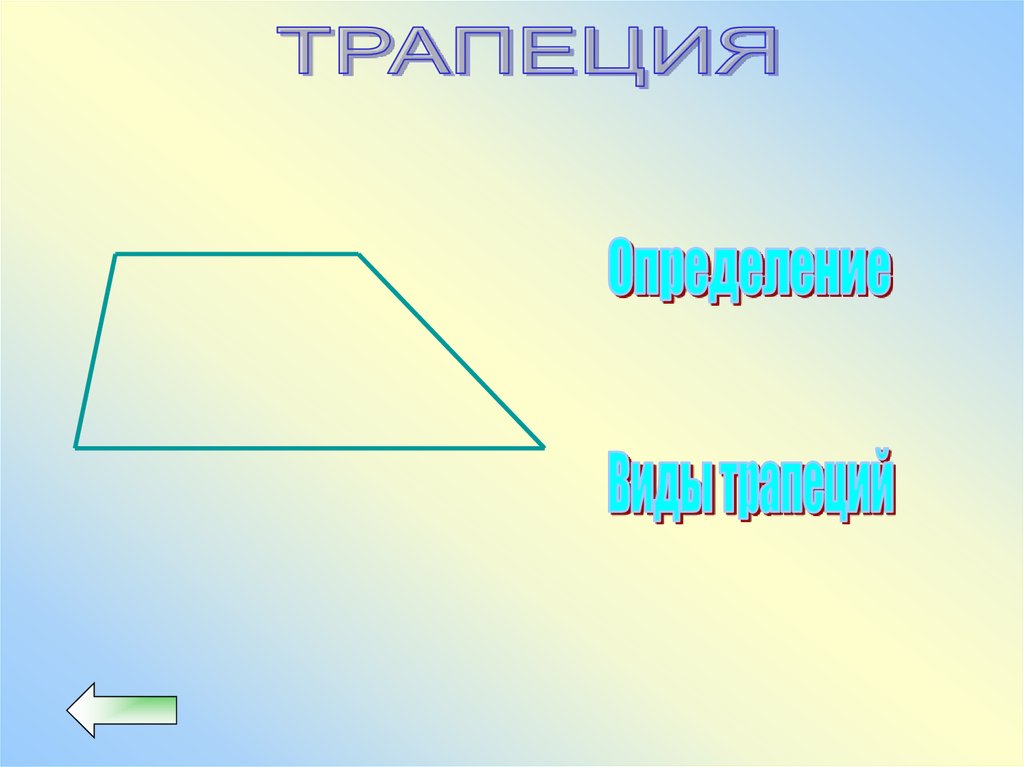
42.

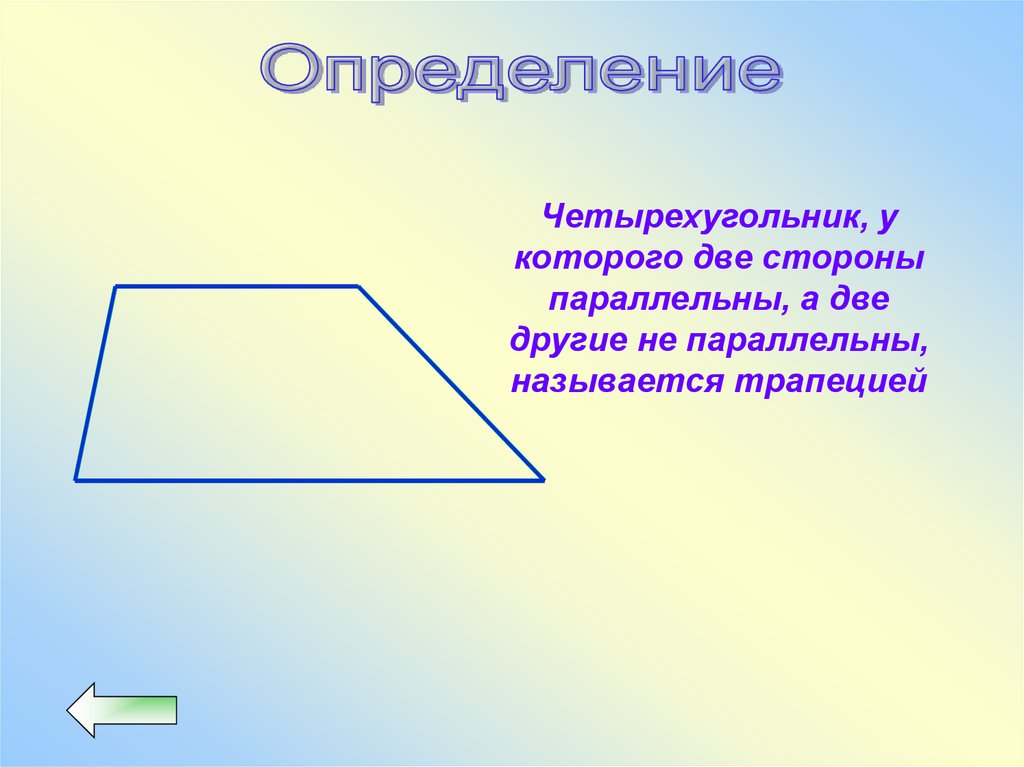
Четырехугольник, у
которого две стороны
параллельны, а две
другие не параллельны,
называется трапецией

43.

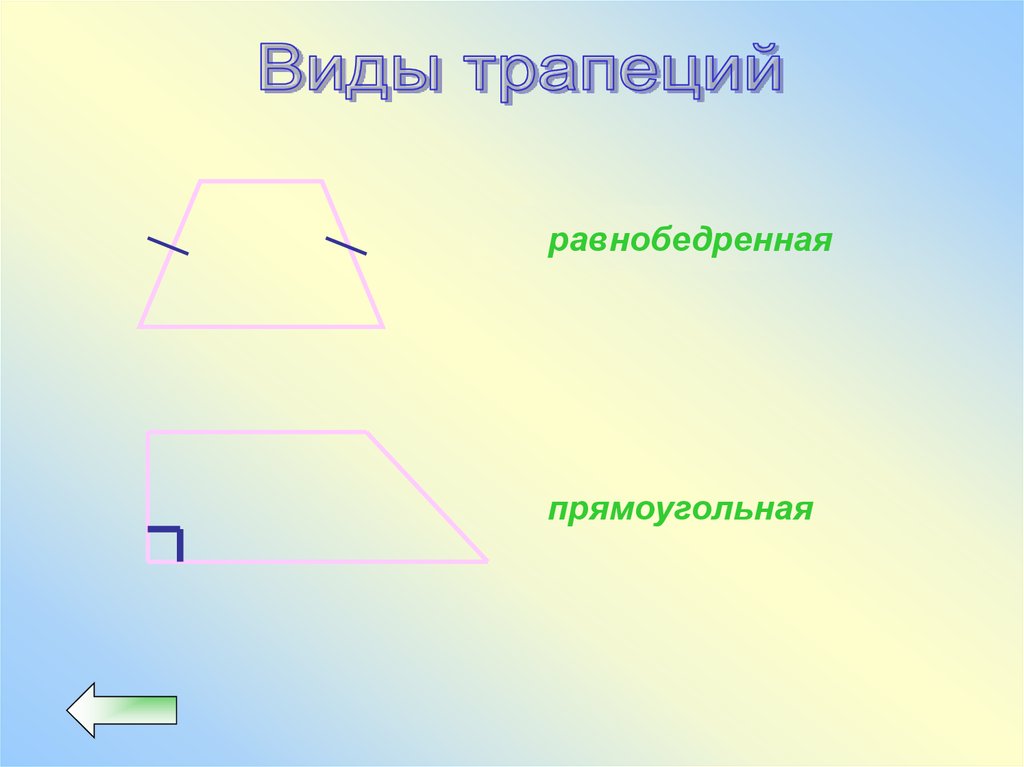
равнобедренная
прямоугольная

44.

45.

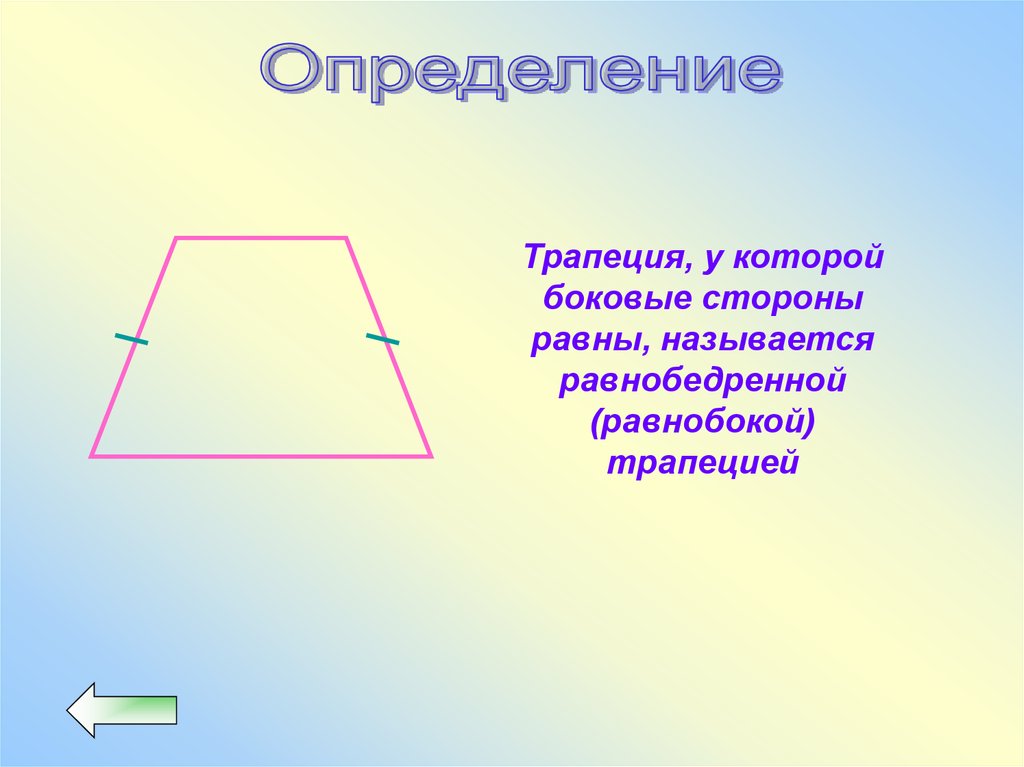
Трапеция, у которой
боковые стороны
равны, называется
равнобедренной
(равнобокой)
трапецией

46.

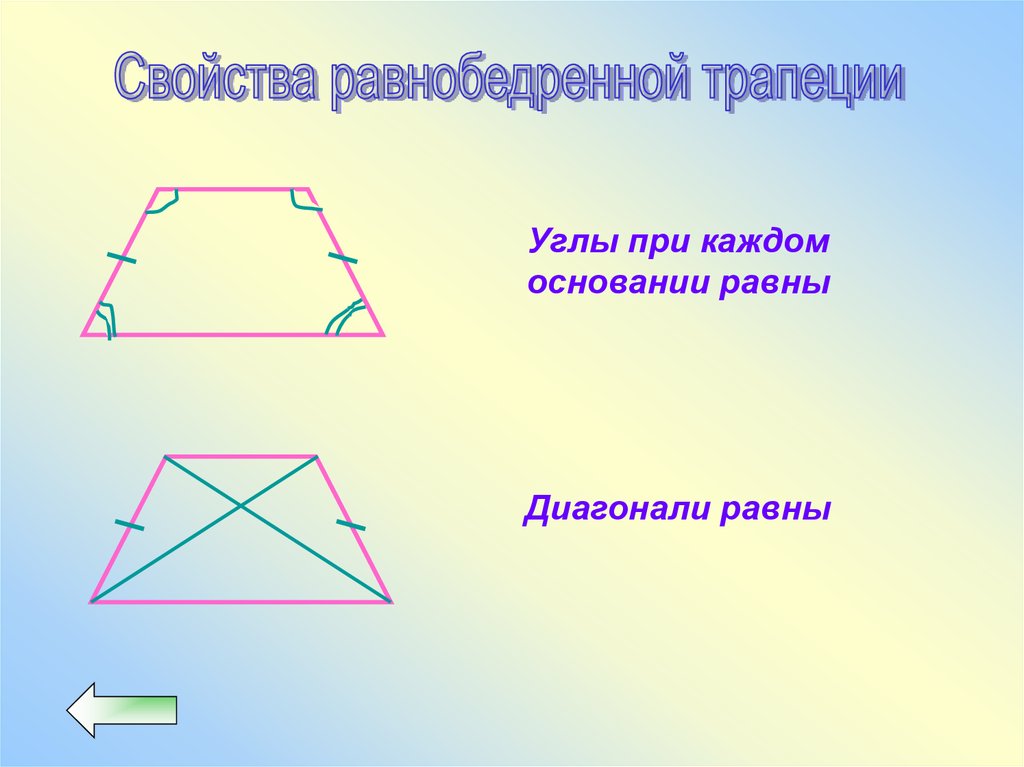
Углы при каждом
основании равны
Диагонали равны

47.

48.

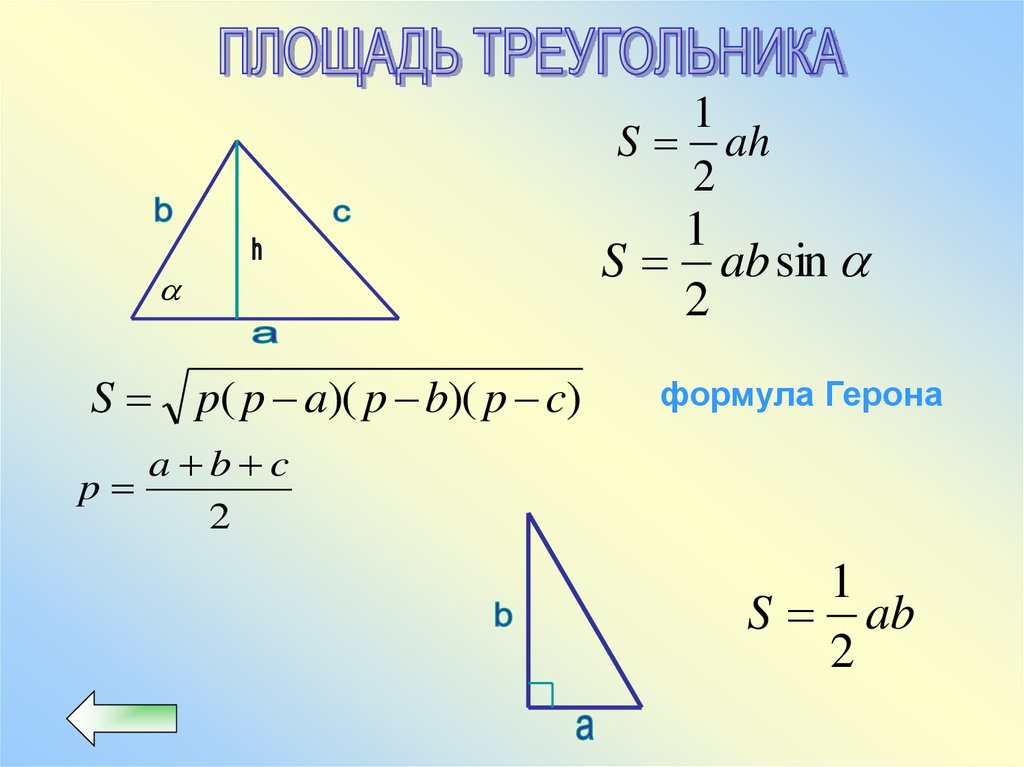
1
S ah
2
S p( p a)( p b)( p c)
1
S ab sin
2
формула Герона
a b c
p
2
1
S ab
2

49.

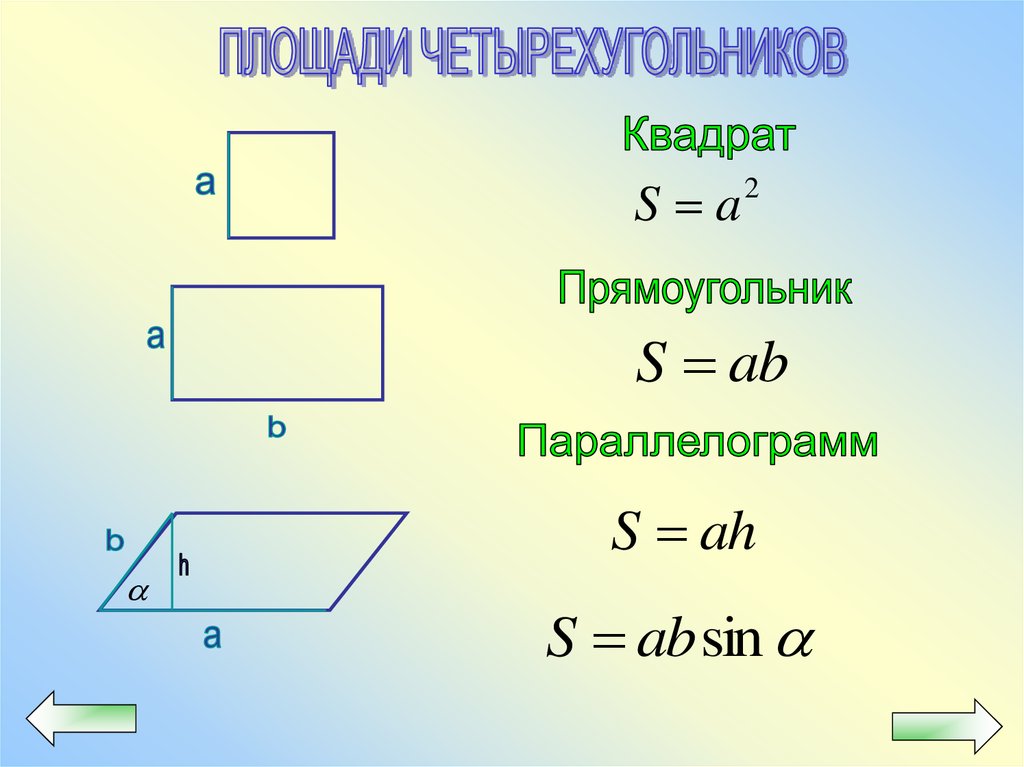
S a
2
S ab
S ah
S ab sin

50.

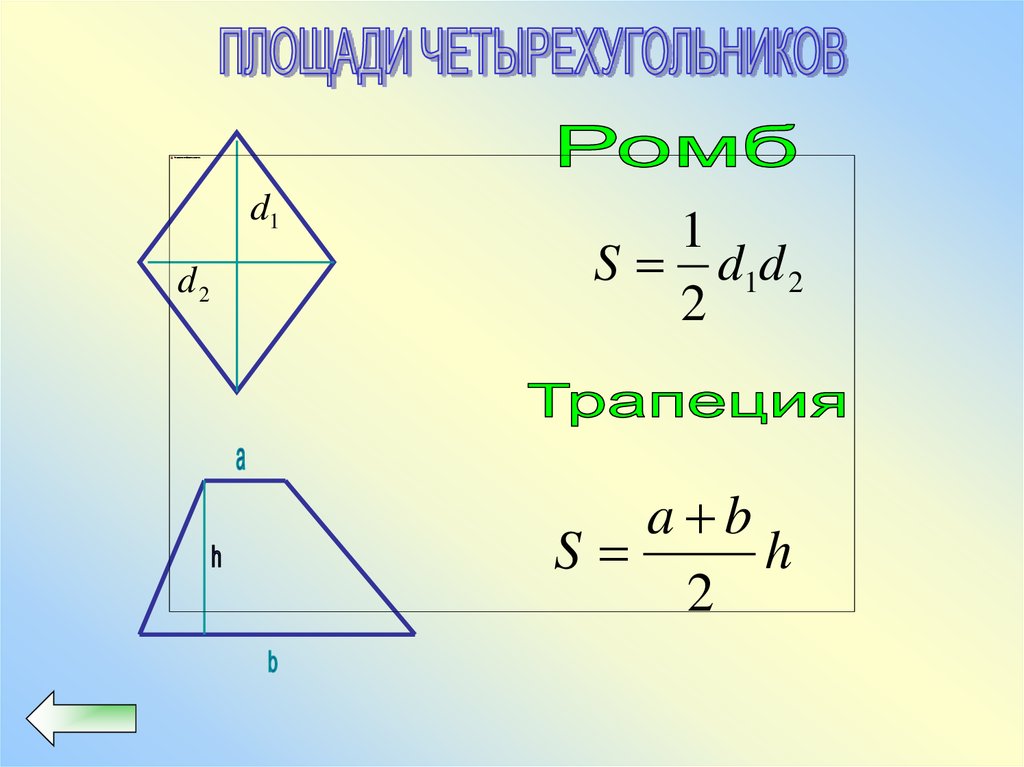
d1
d2
1
S d1d 2
2
a b
S
h
2

51.

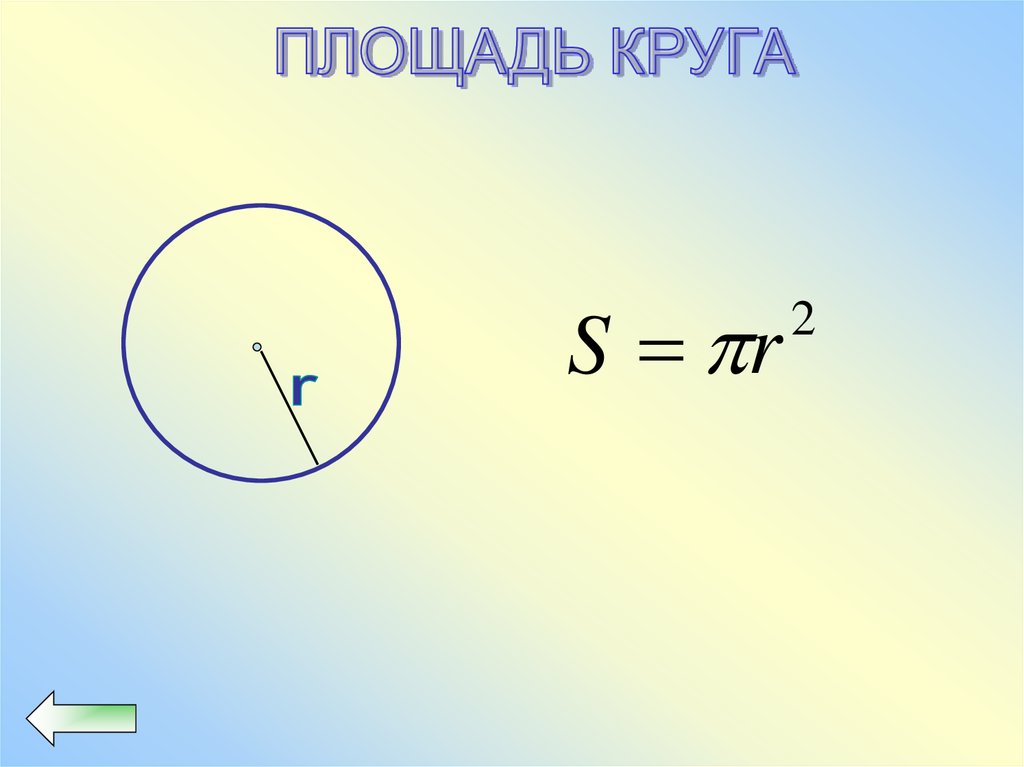
S r
2

52.

53.

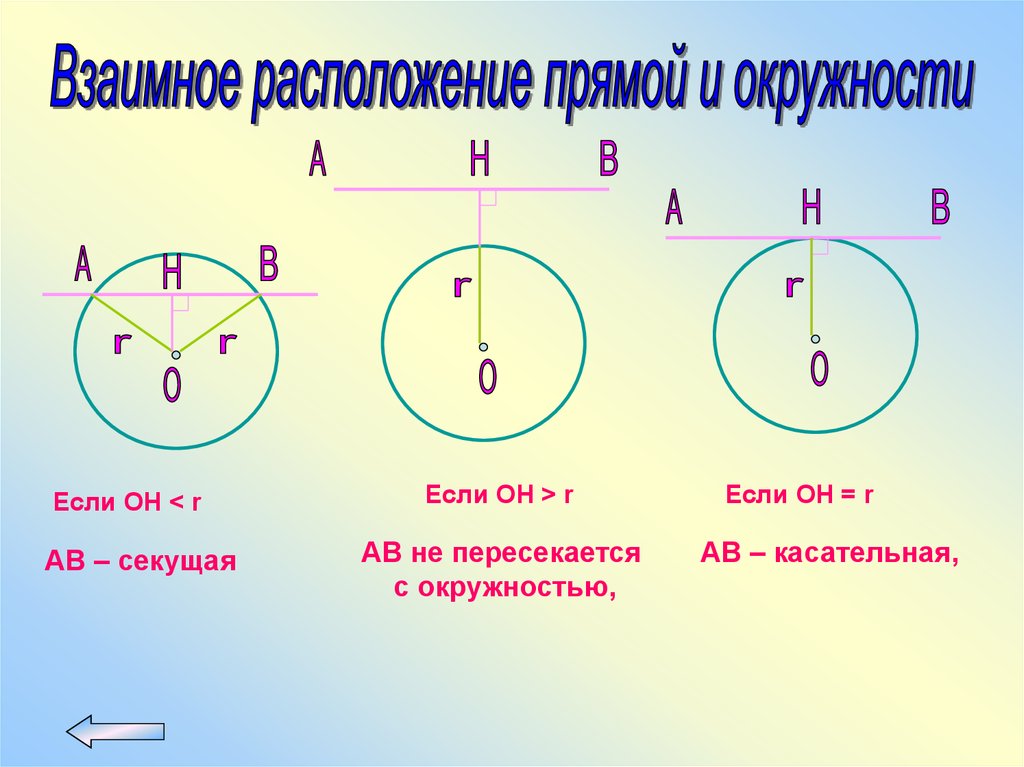
Если OH < r
AB – секущая
Если OH > r
AB не пересекается
с окружностью,
Если OH = r
AB – касательная,

54.

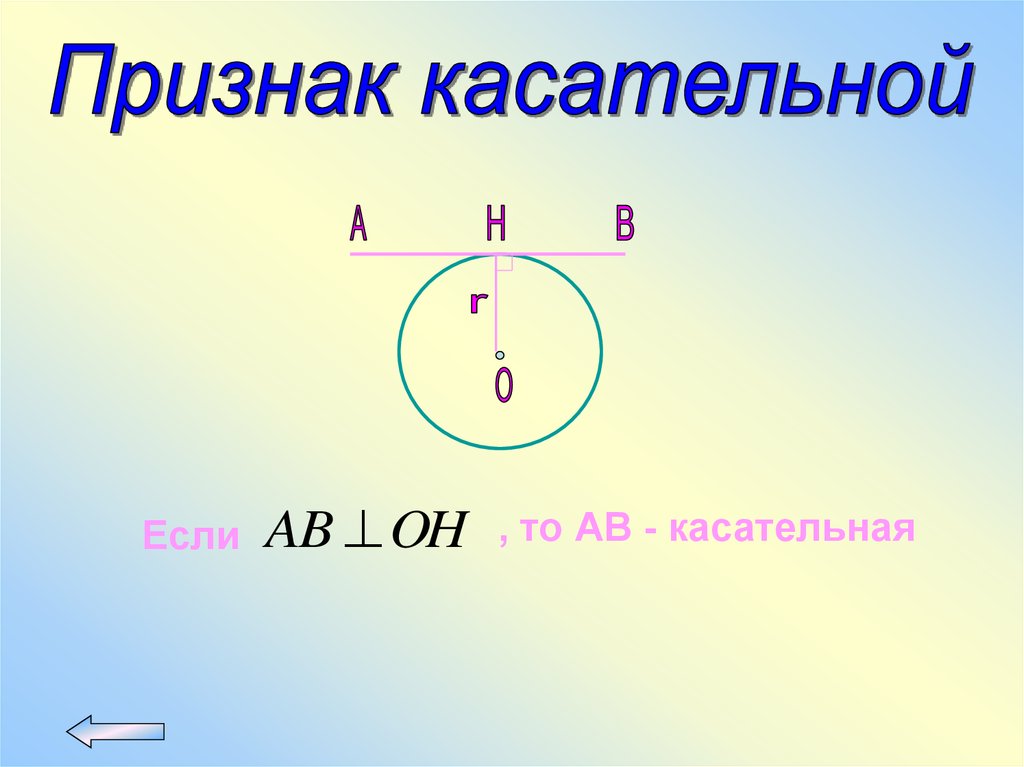
55.

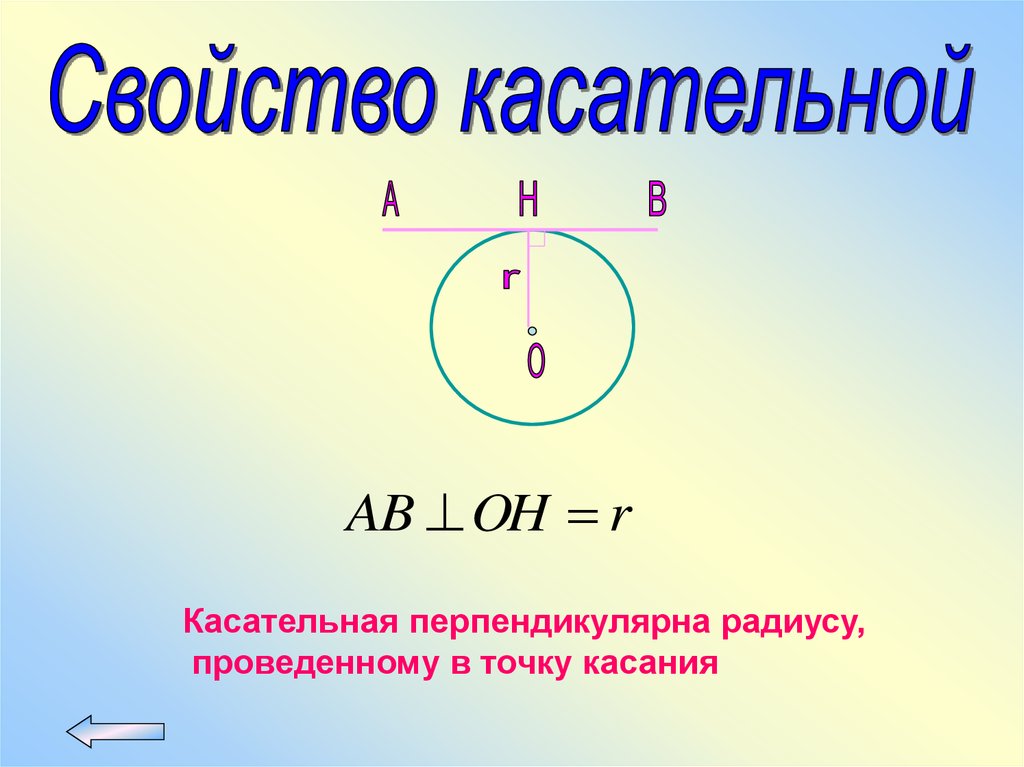
AB OH r
Касательная перпендикулярна радиусу,
проведенному в точку касания

56.

Если
AB OH
, то АВ - касательная

57.

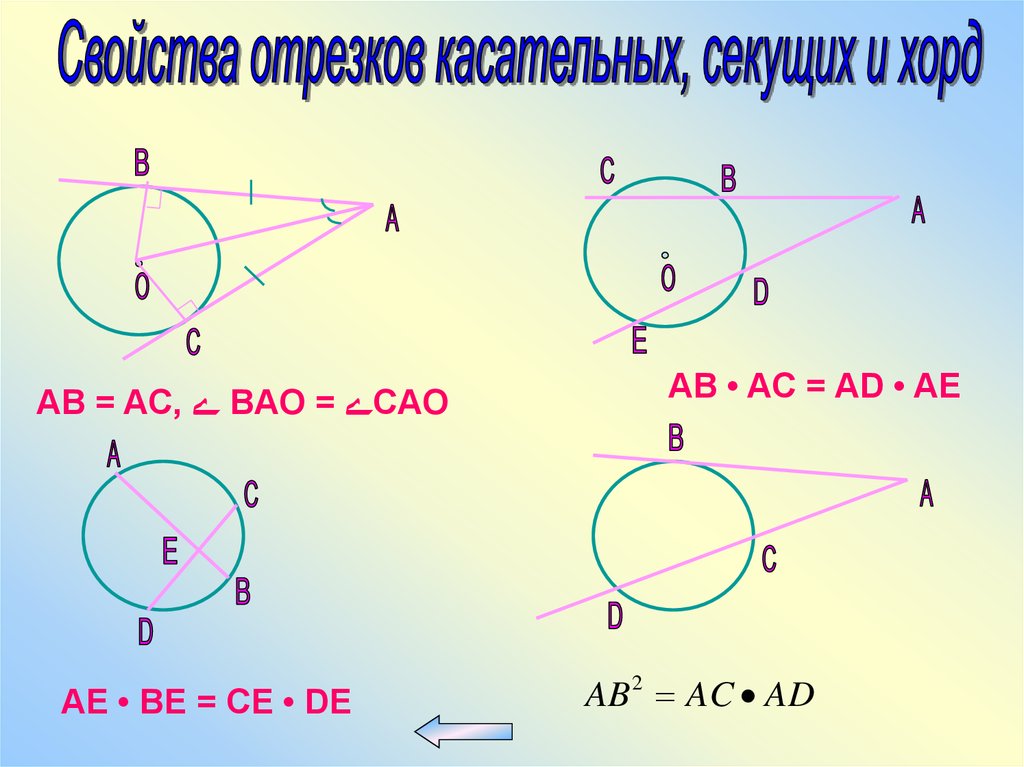
AB = AC, ‫ ے‬BAO = ‫ے‬CAO
AE • BE = CE • DE
AB • AC = AD • AE
AB 2 AC AD

58.

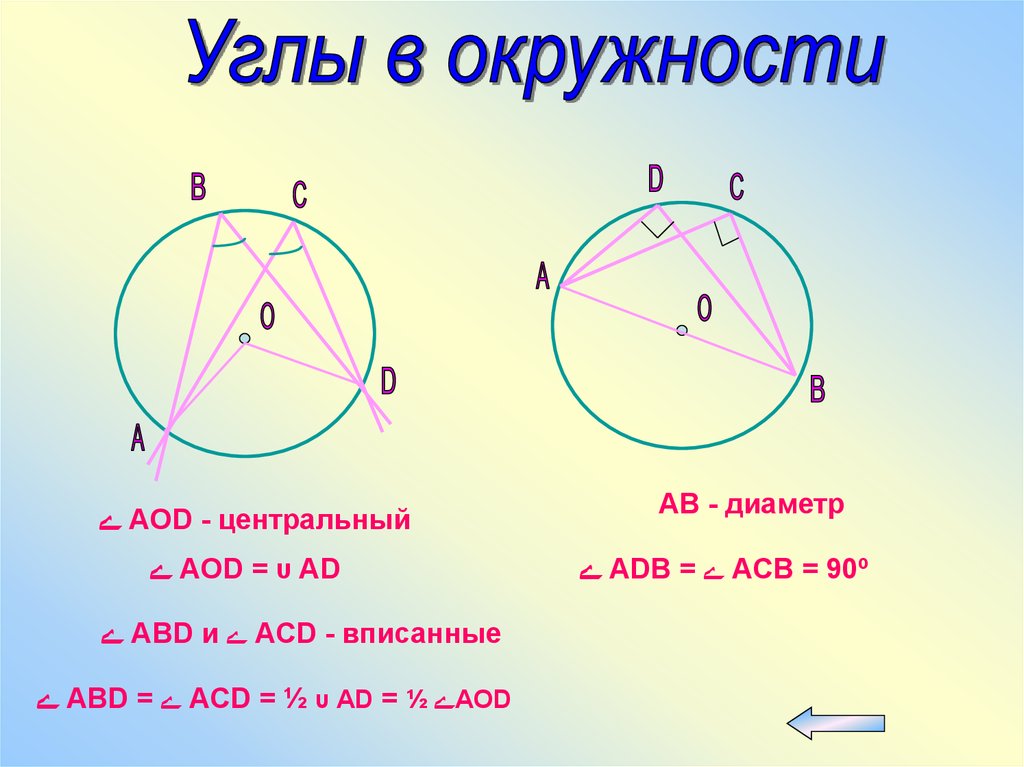
‫ ے‬AOD - центральный
‫ ے‬AOD = υ AD
‫ ے‬ABD и ‫ ے‬ACD - вписанные
‫ ے‬ABD = ‫ ے‬ACD = ½ υ AD = ½ ‫ے‬AOD
AВ - диаметр
‫ ے‬ADB = ‫ ے‬ACB = 90º

59.

60.

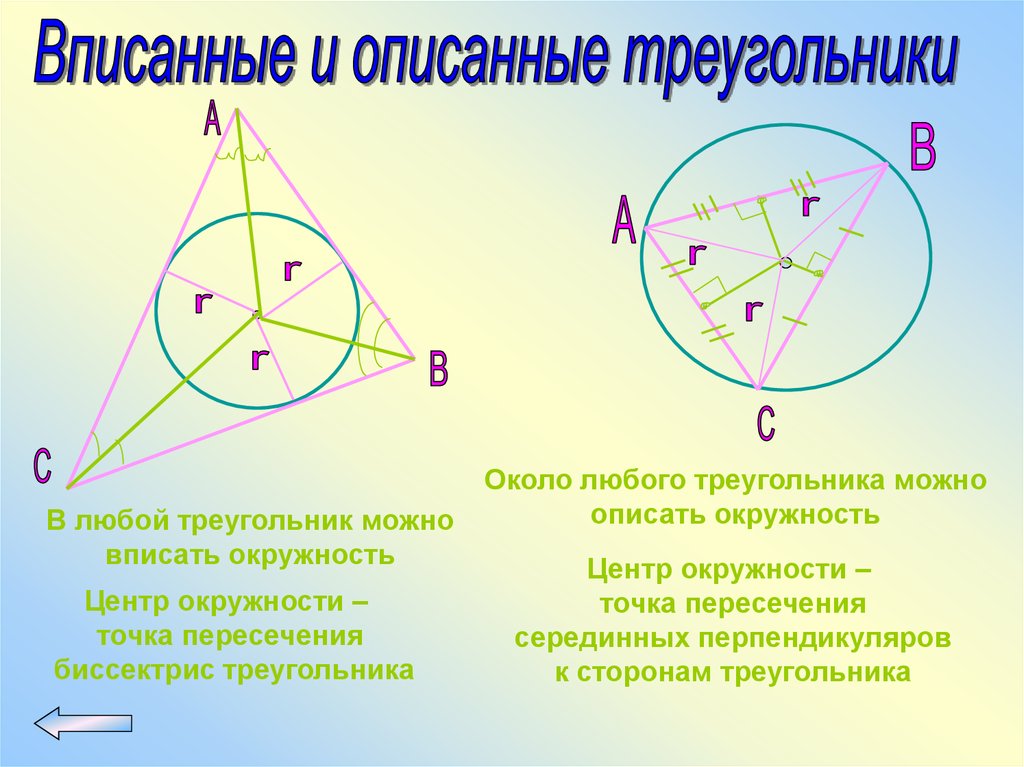
В любой треугольник можно
вписать окружность
Центр окружности –
точка пересечения
биссектрис треугольника
Около любого треугольника можно
описать окружность
Центр окружности –
точка пересечения
серединных перпендикуляров
к сторонам треугольника

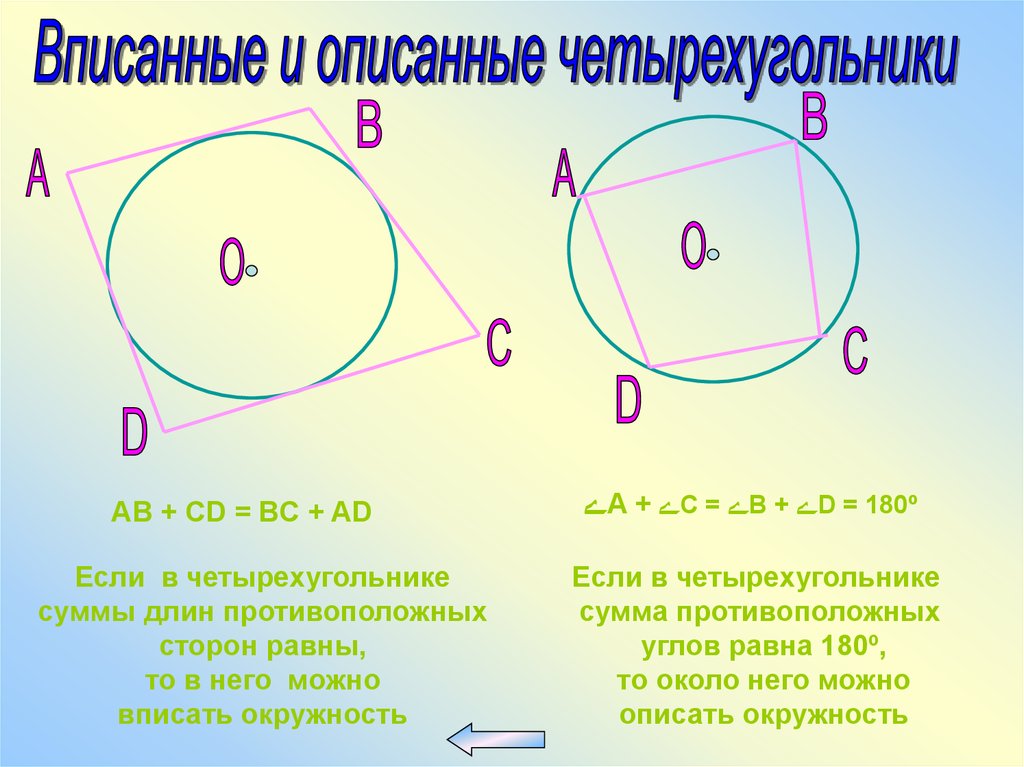
61.

AB + CD = BC + AD
Если в четырехугольнике
суммы длин противоположных
сторон равны,
то в него можно
вписать окружность
‫ے‬A + ‫ے‬C = ‫ے‬B + ‫ے‬D = 180º
Если в четырехугольнике
сумма противоположных
углов равна 180º,
то около него можно
описать окружность

62.

63.

Вектор – это направленный отрезок
а АВ
A( x1; y1 ), B( x2 ; y2 )
a a1;a2
a1 x2 x1; a2 y2 y1
a AB
2
2
a a1 a2

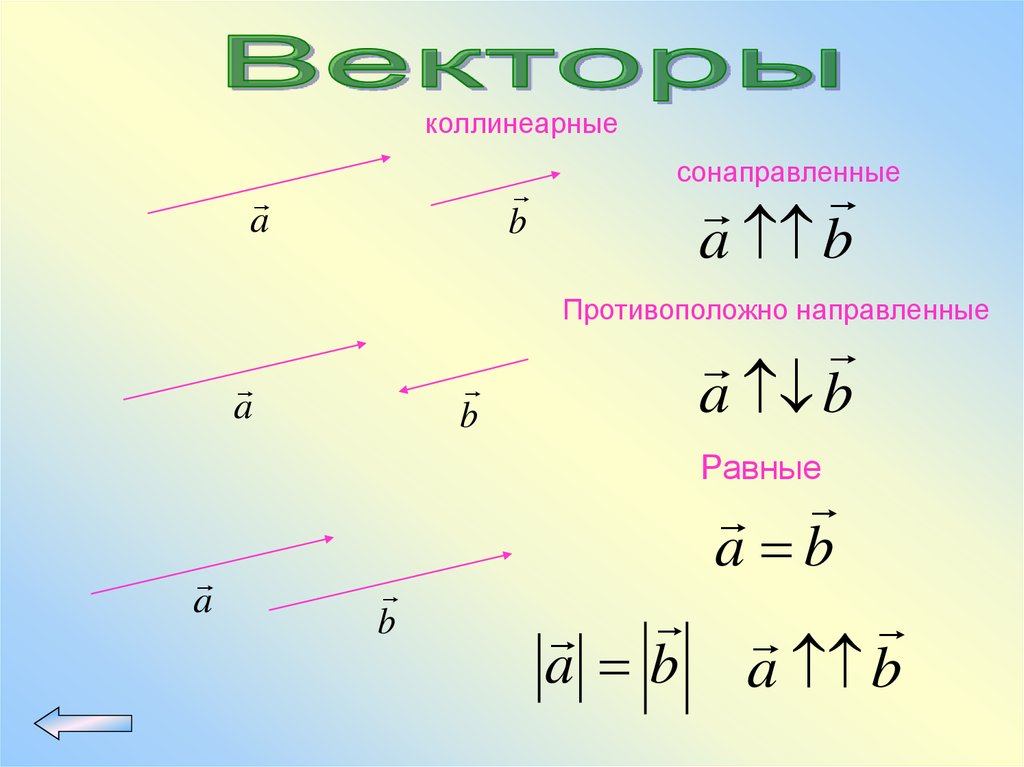
64.

коллинеарные
b
a
сонаправленные
a b
Противоположно направленные
a
b
a b
Равные
a
b
a b
a b a b

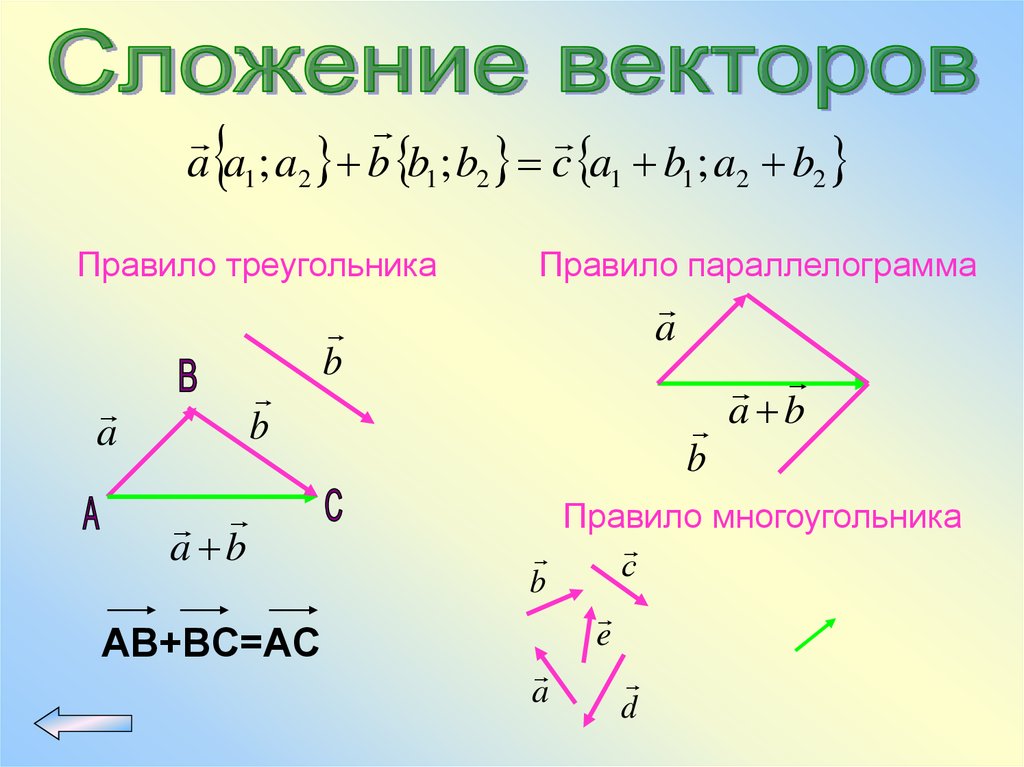
65.

a a1 ; a2 b b1 ; b2 c a1 b1 ; a2 b2
Правило треугольника
b
a
a b
AB+BC=AC
Правило параллелограмма
a
b
a b
b
b
a
Правило многоугольника
с
e
d

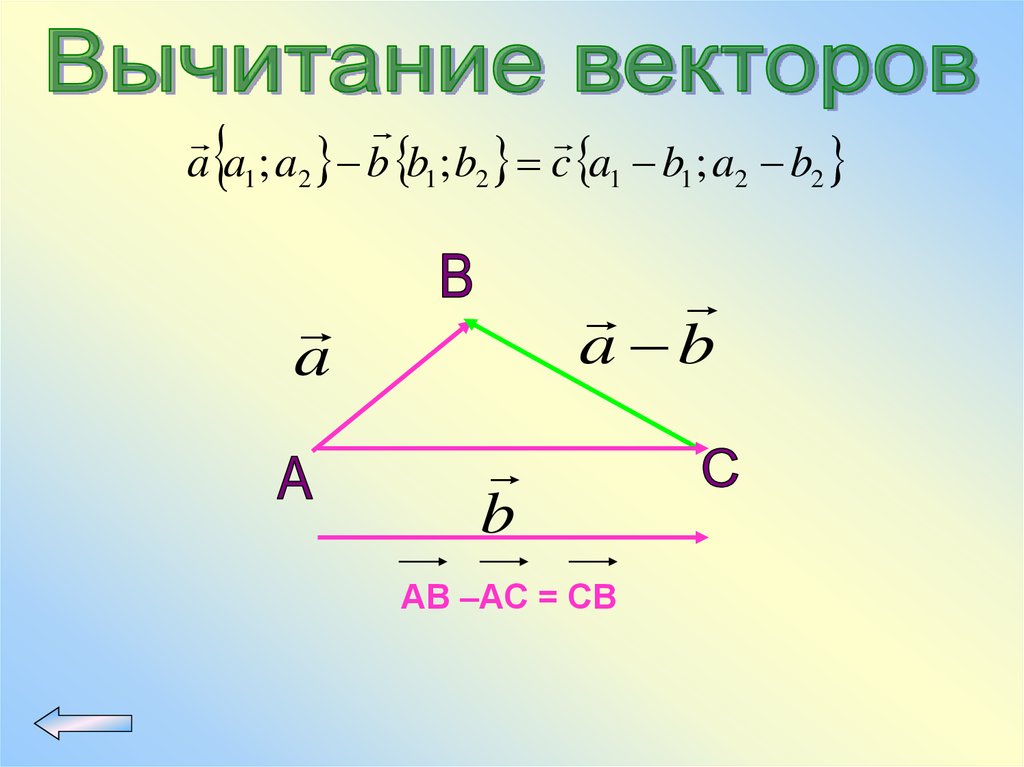
66.

a a1 ; a2 b b1 ; b2 c a1 b1 ; a2 b2
a b
a
b
AB –AC = CB

67.

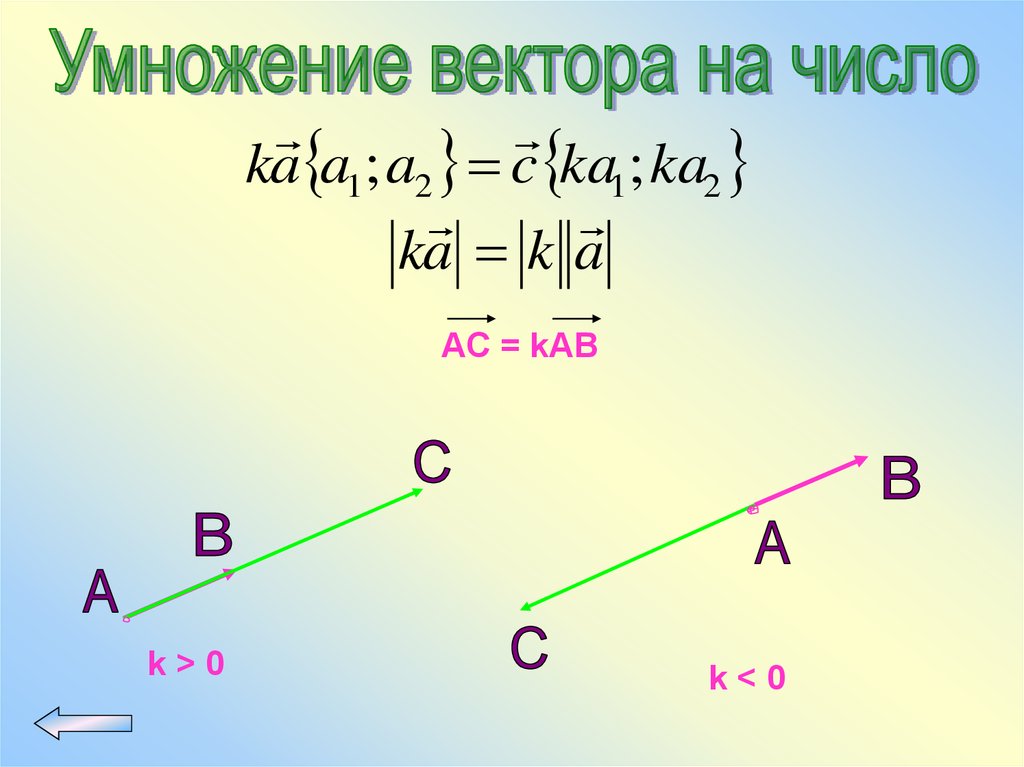
ka a1; a2 c ka1; ka2
ka k a
AC = kAB
k>0
k<0

68.

a
b
a a1 ; a2 b b1 ; b2 a1b1 a2b2
a b a b cos
a
b
a 0; b 0; a b 0 a b

69.

70.

Движение – отображение плоскости на себя,
которое сохраняет расстояния между точками
При движении отрезок отображается
на отрезок
При движении треугольник
отображается на
равный ему треугольник
При движении прямая отображается на прямую,
луч – на луч,
угол – на равный ему угол

71.

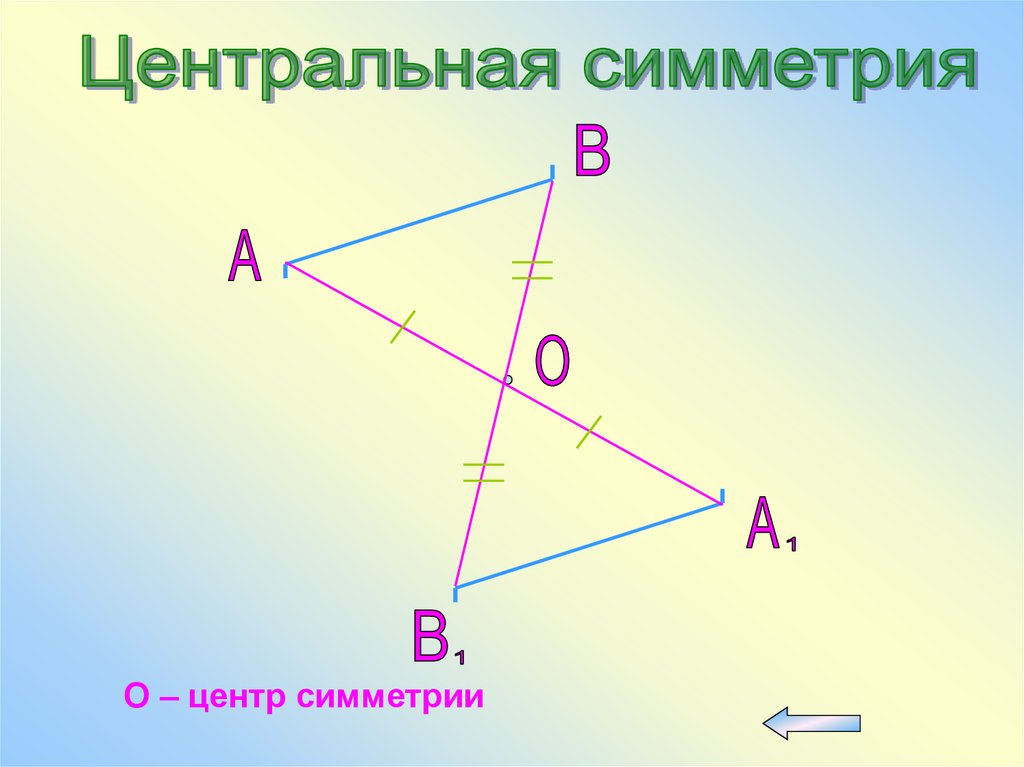
О – центр симметрии

72.

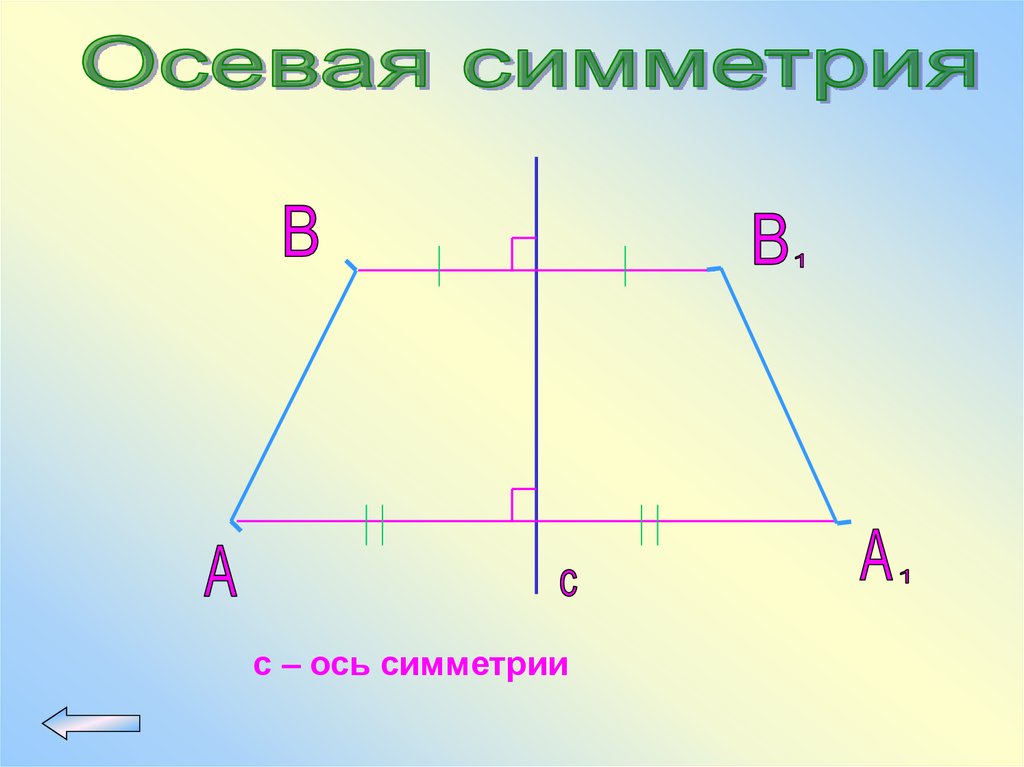
с – ось симметрии

73.

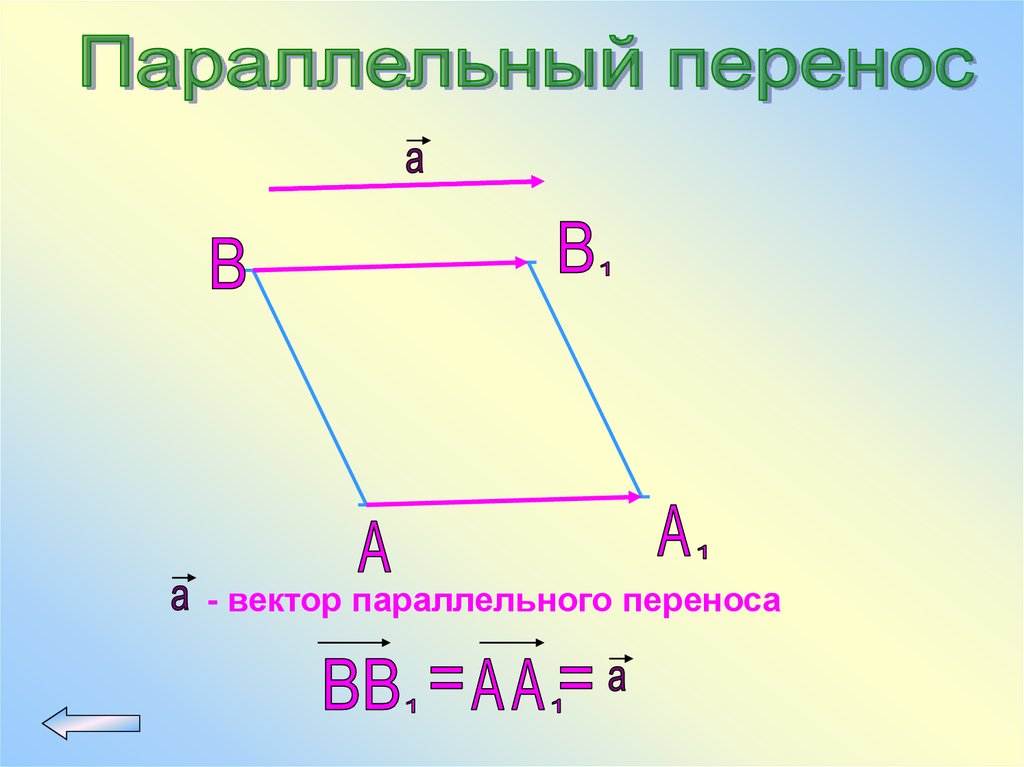
- вектор параллельного переноса

74.

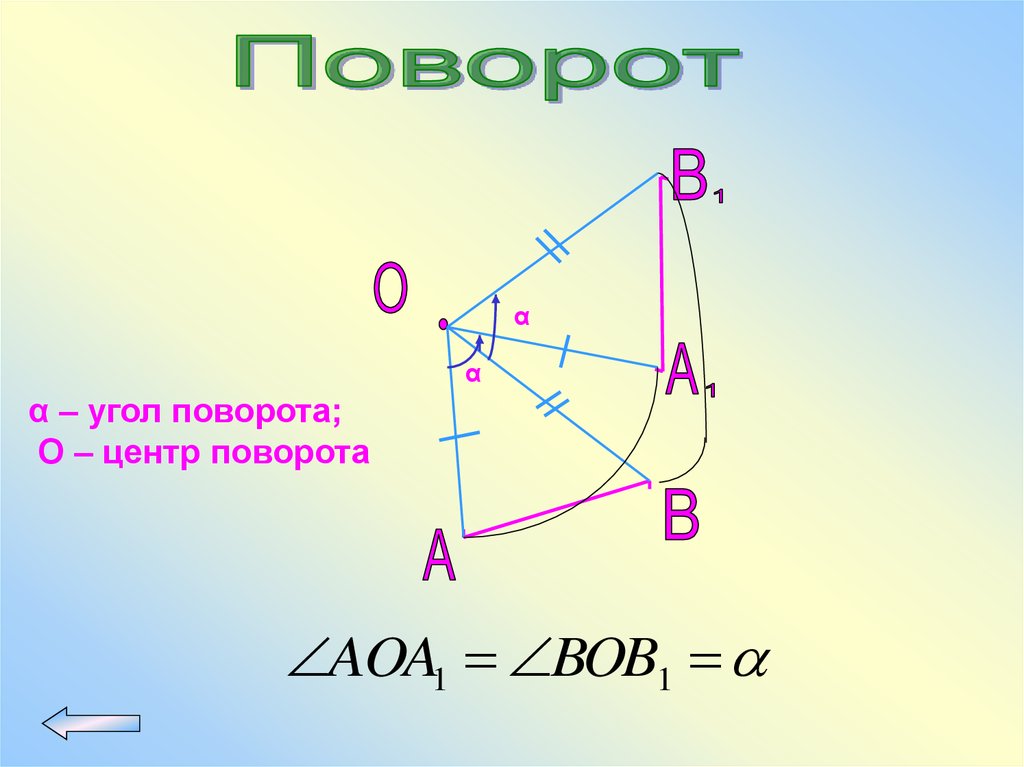
α
α
α – угол поворота;
О – центр поворота
AOA1 BOB1