Зачет по геометрии в 8 классе

1. Зачет по геометрии в 8 классе

2. Билет №1

1)
Дайте определение многоугольника, вершины,
стороны, диагонали и периметра многоугольника.
Запишите формулу суммы углов выпуклого
многоугольника
Многоугольник - часть плоскости, ограниченная замкнутой
ломаной без самопересечений, любые два соседних звена
которой не лежат на одной прямой.
Вершины ломаной называются вершинами многоугольника,
стороны ломаной - сторонами многоугольника
.Диагональ многоугольника - отрезок, соединяющий любые
две не соседние вершины
.Периметр многоугольника - сумма длин всех его сторон
.Выпуклый многоугольник - это многоугольник, лежащий по
одну сторону от любой прямой, содержащей его сторону
.Формула суммы углов выпуклого многоугольника:
180°(n - 2)

3. Вопрос 2

Средняя линия треугольника параллельна третьей
стороне и равна ее половине
.Дано: ΔАВС, КМ - средняя линия.
Доказать: КМ ║ АС, КМ = АС/2
Доказательство:1. Через точку К (середину стороны АВ)
проведем прямую, параллельную стороне АС
.По теореме Фалеса эта прямая разделит сторону ВС
пополам, значит пройдет через точку М
.Средняя линия КМ лежит на прямой, параллельной АС,
значитКМ ║ АС.2. Через точку М проведем прямую,
параллельную стороне АВ.По теореме Фалеса она
разделит сторону АС пополам. Н - середина АС.АКМН параллелограмм, так как КМ ║ АН и МН ║ АК по
построению, значит КМ = АН = АС/2

4. Вопрос 3

Радиус ОВ окружности с
центром в точке О пересекает
хорду АС в точке D и
перпендикулярен ей. Найдите
длину хорды АС, если ВD=1 см, а
радиус окружности равен 5 см.

5. Вопрос 4

Периметр прямоугольника равен 56 а
диагональ равна 20.Найдите площадь
этого прямоугольника
49
Пусть ширина прямоугольника а,
длина в, диагональ с.
Тогда а+в=56:2=28, в=28-а.
с²=а²+в²=а²+(28-а)²;
а²+784-56а+а²=400
а²-28а+192=0
а=16; в=12.
Тогда S = 16*12 = 192

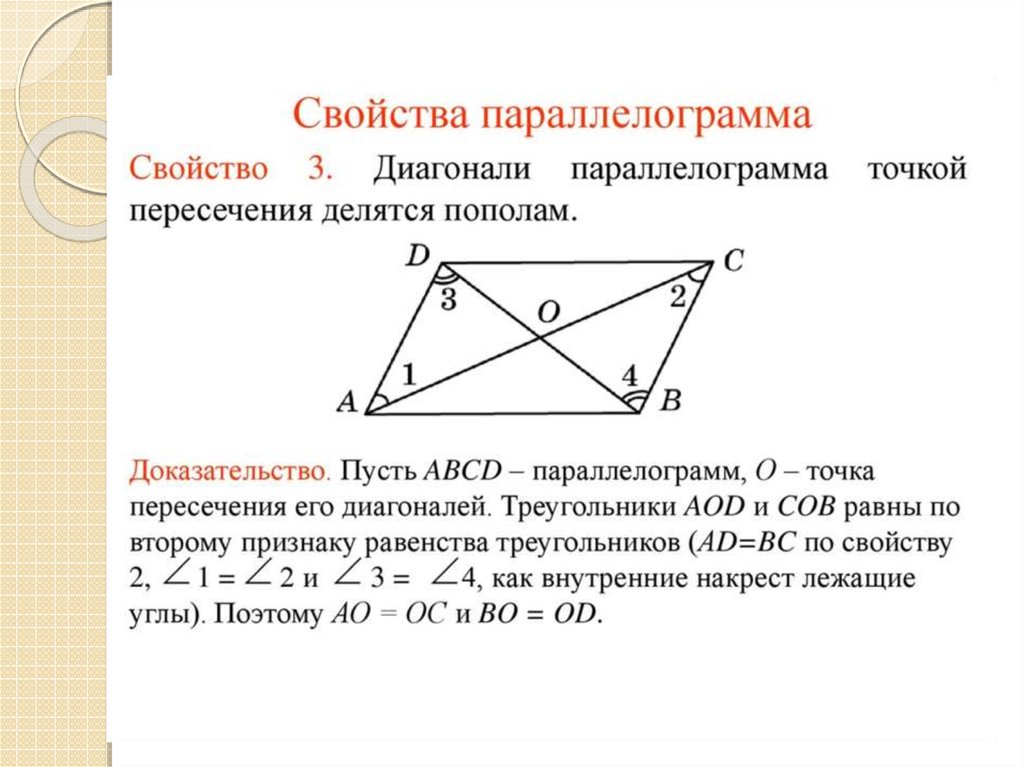
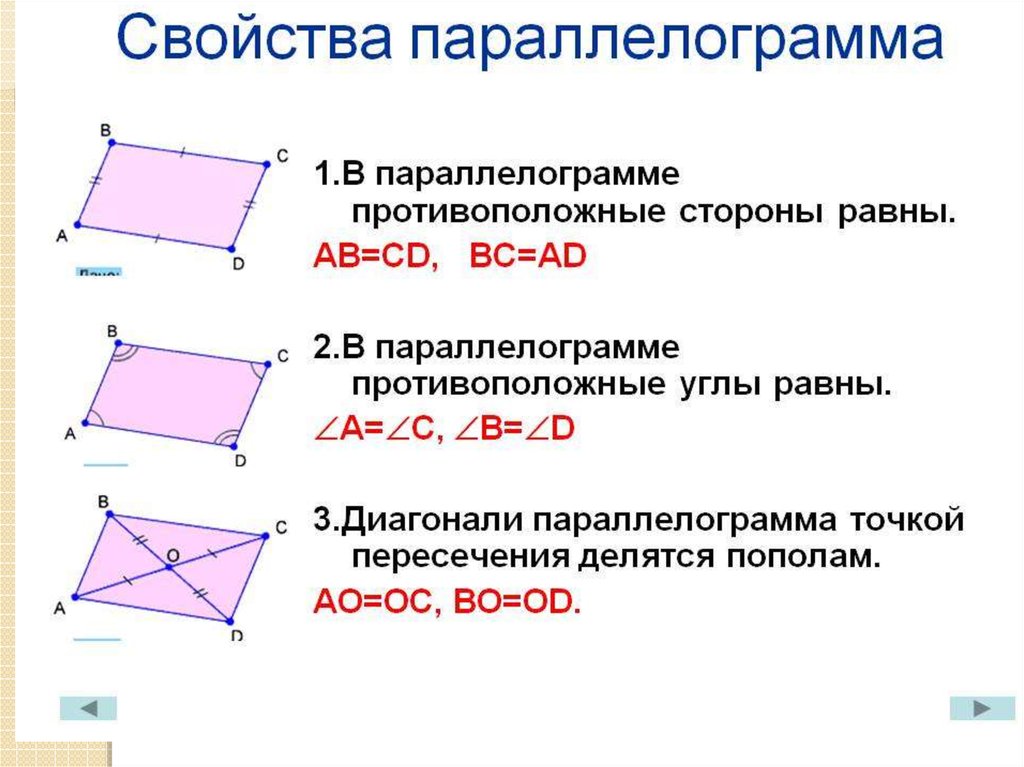
6. Билет 2Дайте определение и свойства параллелограмма.

1)
Билет
2Дайте
определение
и
свойства параллелограмма.
Параллелограмм — это такой
четырехугольник, у которого
противоположные стороны
являются попарно параллельными.
1. Противоположные стороны
тождественны.
2. Противоположные углы
тождественны.
3. Диагонали разделены пополам
точкой пересечения.

7. Докажите свойство медиан треугольника

1)
Докажите
свойство
медиан
треугольника

8.

1)
Проектор полностью освещает экран а высотой 80 см, расположенный на расстоянии 250
см от проектора. На каком наименьшем
расстоянии (в сантиметрах) от проектора
нужно расположить экран б высотой 160 см,
чтобы он был полностью освещён, если настройки проектора остаются неизменными?

9.

Найдите угол ACO, если его сторона СА
касается окружности, О - центр окружности,
а дуга АД окружности, заключённая внутри
этого угла, равна 100°

10. Билет 3

1)
Дайте
определение
прямоугольника.
и
назовите
свойства
Прямоугольник — это четырехугольник,
у которого каждый угол является прямым.
Свойства прямоугольника
1. Прямоугольник —
это параллелограмм.
2. Противоположные стороны равны.
AB = CD,\enspace BC = ADAB=CD,BC=AD

11.

3. Противоположные стороны
параллельны.
AB \parallel CD,\enspace BC \parallel
ADAB∥CD,BC∥AD
4. Прилегающие стороны
перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp
CD,\enspace CD \perp AD,\enspace
AD \perp
ABAB⊥BC,BC⊥CD,CD⊥AD,AD⊥AB

12.

5. Диагонали прямоугольника равны.
AC = BDAC=BD
6. Квадрат диагонали равен сумме
квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы
Пифагора.
AC^2=AD^2+CD^2AC​2​=AD​2​+CD​2​
7. Диагональ делит прямоугольник
на два одинаковых прямоугольных
треугольника.
\

13.

8. Точка пересечения диагоналей
делит их пополам.
AO = BO = CO = DOAO=BO=CO=DO

14. Докажите теорему Пифагора.

В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Доказательство:Пусть дан прямоугольный
треугольник с катетами а и b и гипотенузой с
.Составим из четырех таких треугольников
квадрат со стороной а + b как на рисунке.
Внутри получим квадрат со стороной с.
Площадь большого квадрата равна сумме
площадей составляющих его фигур:S = 4·SΔ +
c² = 4 · ab/2 + c²илиS = (a + b)²
Приравняем правые части:2ab + c² = (a + b)²2ab
+ c² = a² + b² + 2abc² = a² + b²Что и требовалось
доказать.

15. Найдите величину (в градусах) вписанного угла а, опирающегося на хорду АВ, равную радиусу окружности.

Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник
AOB
—
равносторонний,
следовательно, все его углы равны 60°.
Угол AOB — центральный и равен 60°
Угол ACB — вписанный и опирается на ту же
дугу, что и угол AOB. Таким образом,
Ответ: 30.

16.

Прямая, параллельная основаниям МР и
NKтрапеции MNKP , проходит через точку
пересечения диагоналей трапеции и
пересекает её боковые стороны MN u КР в
точках А и B соответ ственно. Найдите длину
отрезка АВ, если МР = 40см, NK=24cм

17. Билет №4 Дайте определение и назовите свойства ромба.

Ромб
Ромб — это четырехугольник, имеющий равные
длины сторон.
Ромб является частным случаем параллелограмма.
Ромб имеющий прямые углы является квадратом.
Свойства ромба
1. Противолежащие стороны ромба
параллельны и равны.
AB \parallel CD,\;BC \parallel ADAB∥CD,BC∥AD
A2. Диагонали ромба перпендикулярны.
AC\perp BDAC⊥BD
B = CD,\;BC = ADAB=CD,BC=AD

18.

3. Точка пересечения диагоналей делит
их пополам.
AC=2\cdot AO=2\cdot COAC=2⋅AO=2⋅CO
BD=2\cdot BO=2\cdot DOBD=2⋅BO=2⋅DO
4. Диагонали ромба являются
биссектрисами его углов.
\angle 1 = \angle 2; \; \angle 5 = \angle
6∠1=∠2;∠5=∠6;
\angle 3 = \angle 4; \; \angle 7 = \angle
8∠3=∠4;∠7=∠8.
Доказательство
5. Диагонали образуют из ромба
4 прямоугольных треугольника.

19.

Теорема 1. Вписанный угол
измеряется половиной дуги, на
которую он опирается.
Доказательство.
Рассмотрим три случая
расположения луча BO
относительно угла ABC.

20.

1)
Два парохода вышли из порта, следуя один на
север, другой на запад. Скорости их равны
соответственно 15 км/ч и 20 км/ч. Какое
расстояние (в километрах) будет между ними
через 2 часа?
Судя по движению катеров они
представляют собой прямоугольный
треугольник. Где путь 1 и 2 парохода катеты, а расстояние между ними
гепотинуза.1) 15*2=30 км прошел 1
парохода за 2 часа2) 20*2=40 км прошел 2
парохода за 2 часа3) √(30²+40²)=50 км
расстояние между пароходами
Ответ 50 км5ответов

21.

22. Билет 5

1)
Дайте определение трапеции. Назовите виды
трапеций.
Трапецией называется такая фигура, у
каторой две стороны паралельны, а
две другие не---паралельны. Трапеции
бывают трех видов, а
именно:прямоугольная-у каторой
прямой угол равен 90 градусов,
равнобедренная и

23.

24.

25.

26. Билет 7

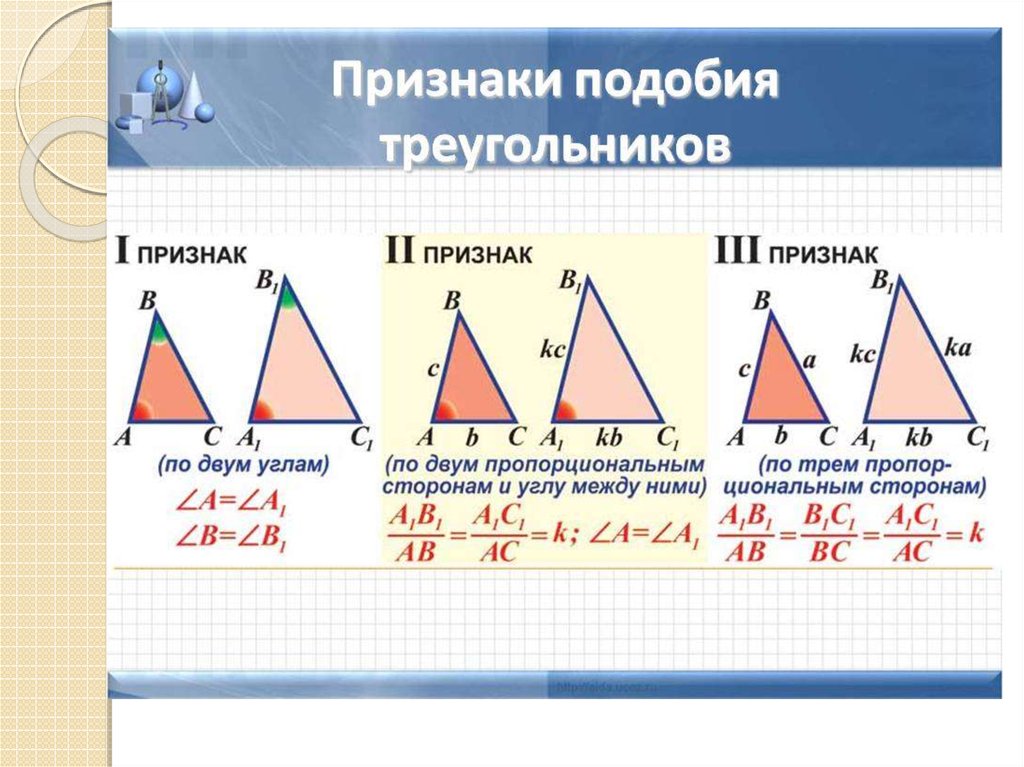
1)
Дайте
определение
подобных
треугольников. Назовите признаки
подобия треугольников.

27.

28.

29.

30.

Свойство касательной: касательная к
окружности перпендикулярна к радиусу,
проведенному в точку касания, то есть ВО
⊥ AB.
Диаметр окружности в два раза меньше
за радиус, то есть BO=OC=7.5/2=3.75 .
Тогда из прямоугольного треугольника
ABO:
Тогда
Ответ: 8.

31. Билет 7

Дайте
определение
синуса,
косинуса
и
тангенса острого угла
прямоугольного треугольника.
Синусом острого угла прямоугольного
треугольника называется отношение
противоположного катета к гипотенузе;
Косинусом - отношение другого катета
к гипотенузе;
Тангенс - отношение
противоположного катета к тому
который рядом с углом.

32.

33.

1)
Найдите
градусную
меру
угла
МОN,
если известно, NP диаметр, а градусная
мера угла MNP равна 18°.

34.

В
треугольнике
АВС
отмечены
середины
М
и
N
сторон
ВС
и
АС
соответственно.
Площадь треугольника СNМ равна 57.
Найдите площадь четырёхугольника
АВМN.
1)
Ответ: 171.

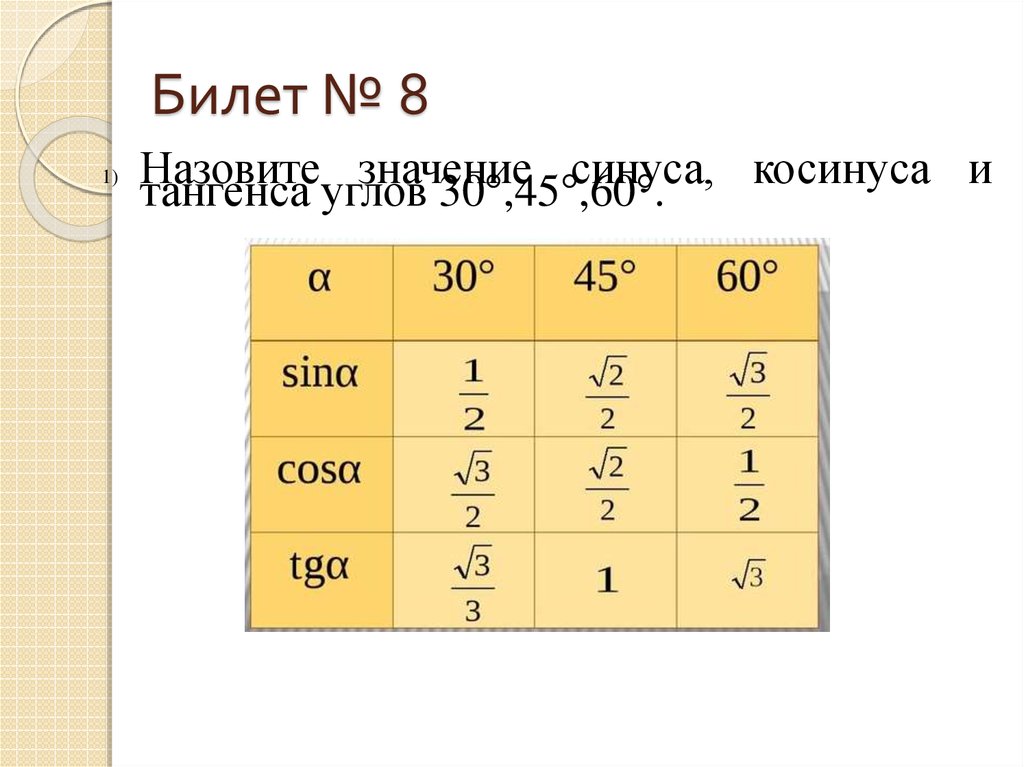
35. Билет № 8

1)
Назовите
значение
синуса,
косинуса
и
тангенса углов 30°,45°,60°.

36.

37.

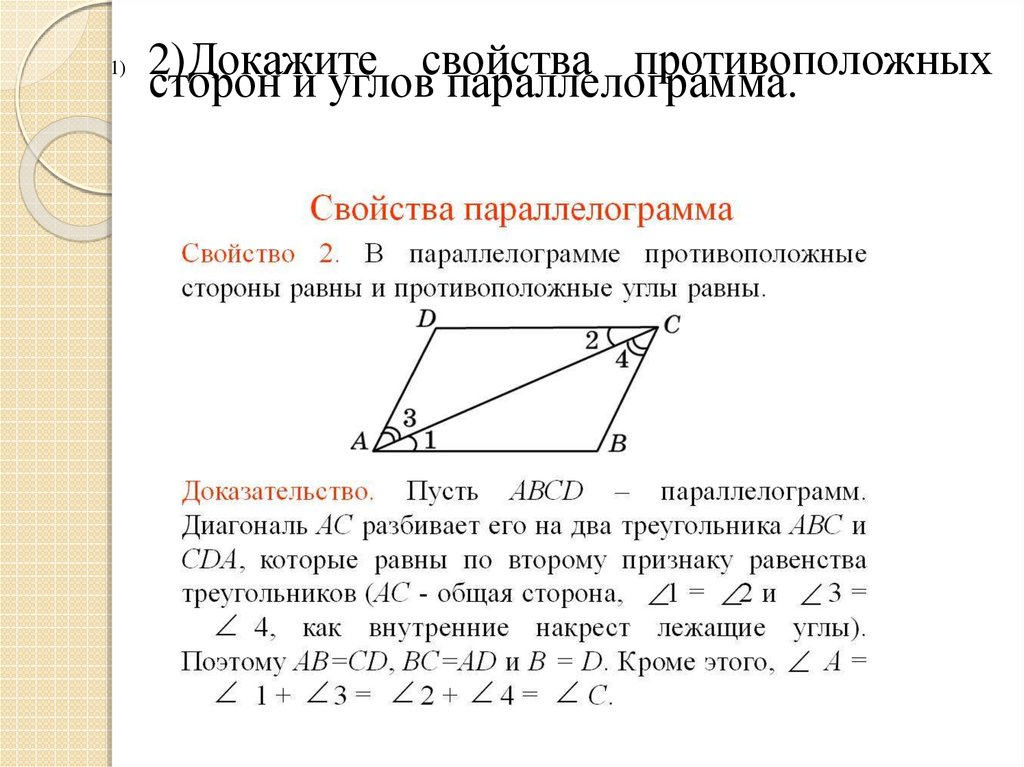
1)
2)Докажите
свойства
противоположных
сторон и углов параллелограмма.

38.

1)
У
треугольника
со
сторонами
16
и
2
проведены высоты к этим сторонам.
Высота,
проведённая
к
первой
стороне,
равна
1.
Чему
равна
высота,
проведённая
ко второй стороне?
Пусть AB - сторона длиной 16, а AC сторона длиной 2.
Задачу легко решить через площадь
треугольника.
Площадь треугольника равна половине
произведения высоты на сторону, к
которой высота проведена. Следовательно:
S=AB*CD/2=16*1/2=8
Так же: S=AC*BE/2
8=2*BE/2
16=2*BE
BE=8
Ответ: 8

39.

1)
Из
точки
А
проведены
две
касательные
к окружности с центром в точке О.
Найдите
радиус
окружности,
если
угол
между
касательными
равен
60°,
а
расстояние от точки А до точки О равно
8.

40. Билет 9

Дайте определение секущей и
касательной к окружности
1)Прямая, проходящая через
точку окружности
перпендикулярно к радиусу,
проведённому в эту точку,
называется касательной. При
этом данная точка окружности
называется точкой касания.
2)Прямая, проходящая через две
точки окружности, называется
секущей.

41.

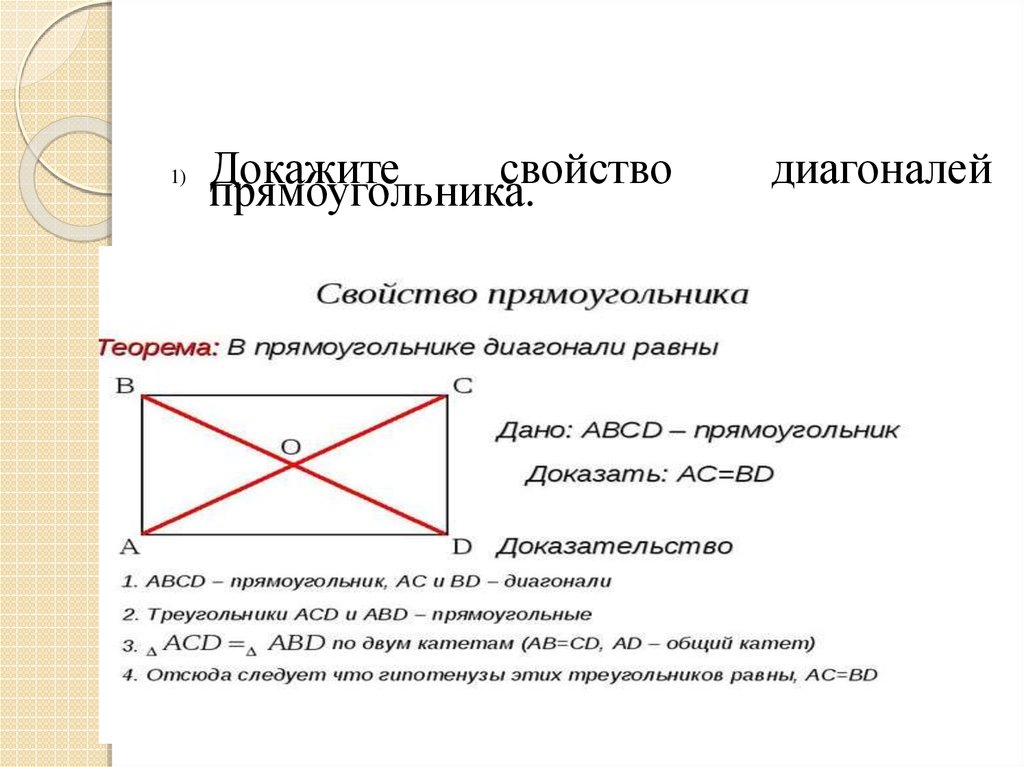
1)
Докажите
свойство
прямоугольника.
диагоналей

42.

1)
3)В
60
м
одна
от
другой
растут
две
сосны. Высота одной 31 м, а другой -6
м.
Найдите
расстояние
(в
метрах)
между их верхушками.

43.

Окружность
пересекает
стороны
АВ
и
АС треугольника АВС в точках К и Р
соответственно
и
проходит
через
вершины
В
и
С.
Найдите
длину
отрезка
КР, если
АК = 18, а сторона АС в 1,2 раза больше
стороны ВС.
1)

44. Билет 10

Дайте
определение
вписанного
и
центрального углов окружности.
Вписанный угол - угол, вершина
которого лежит на окружности, а
стороны этого угла пересекают
окружность
Центральный угол - угол, вершина
которого центр окружности.
1)

45.

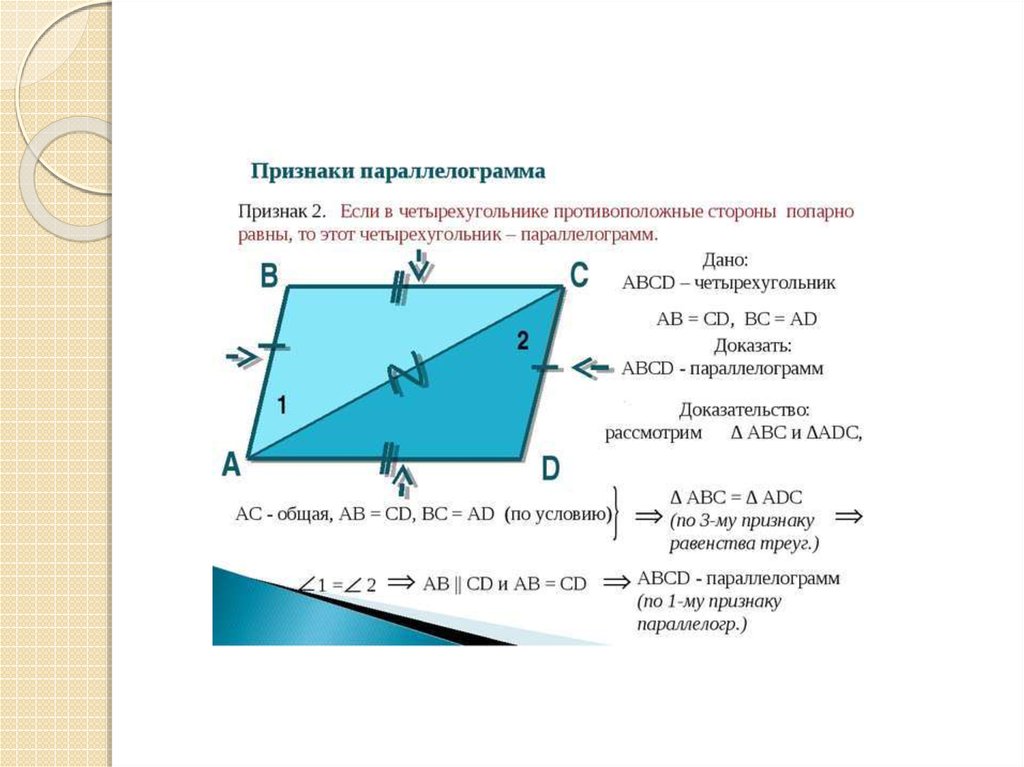
Докажите признак параллелограмма по
двум противоположным сторонам,
которые равны и параллельны

46.

47.

1)
Человек
ростом
1,7
м
стоит
на
расстоянии 8 шагов от столба, на
котором
висит
фонарь.
Тень
человека
равна
четырем
шагам.
На
какой
высоте
(в метрах) расположен фонарь?

48.

1)
Основания
равнобедренной
трапеции
равны 8 и 18, а периметр равен 56.
Найдите площадь трапеции.