Курс геометрии за 8 класс

1. Геометрия 8 класс.

2. Содержание

Четырехугольники
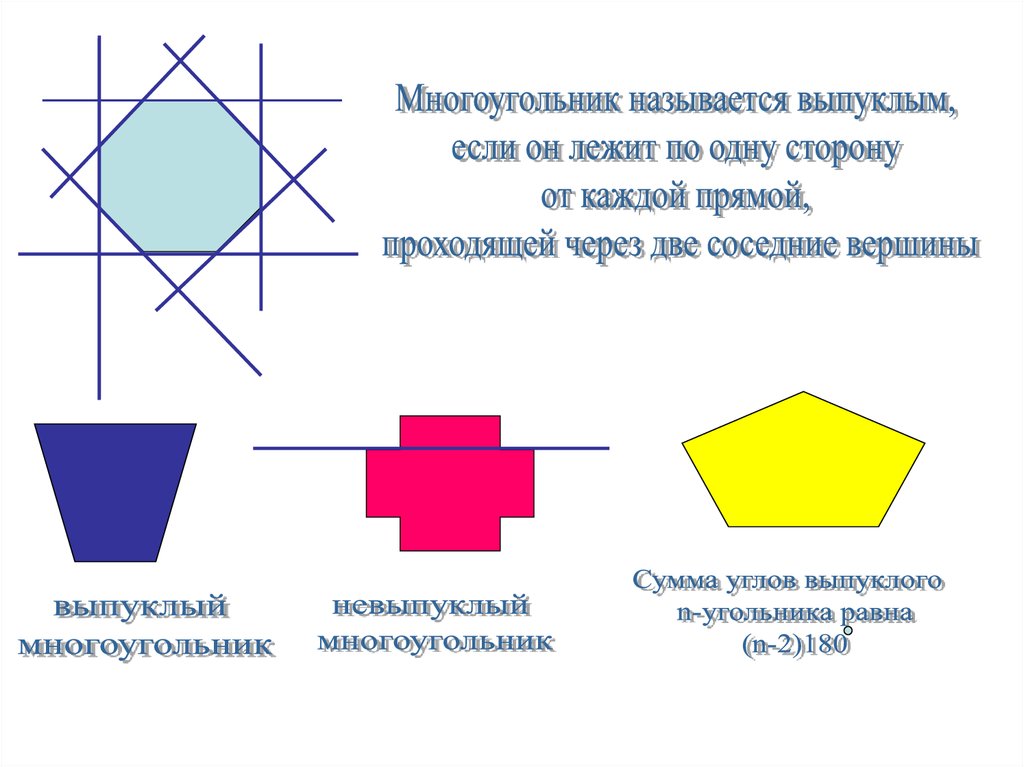
Многоугольники
Параллелограмм
Трапеция
Теорема Фалеса
Прямоугольник
Ромб
Квадрат
Осевая и центральная симметрия
Площадь
Свойства площадей
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Подобные треугольники
Определение подобных треугольников
Признаки подобия треугольников
Средняя линия треугольника
Соотношения между сторонами и углами прямоугольного треугольника

3.

4.

5.

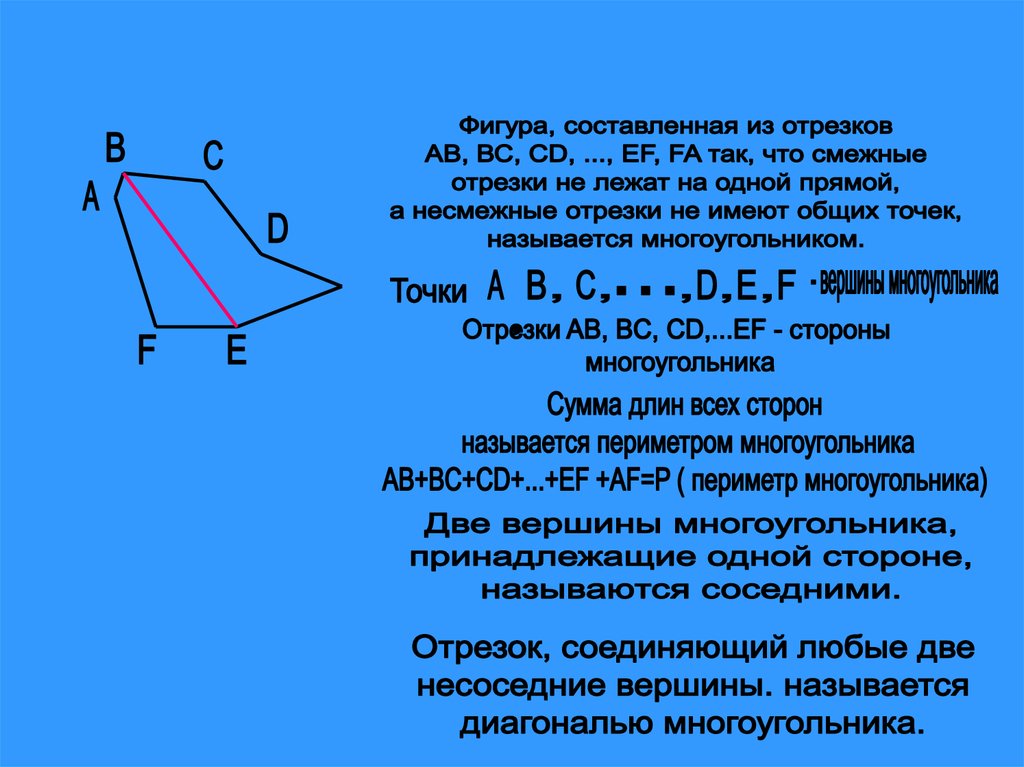
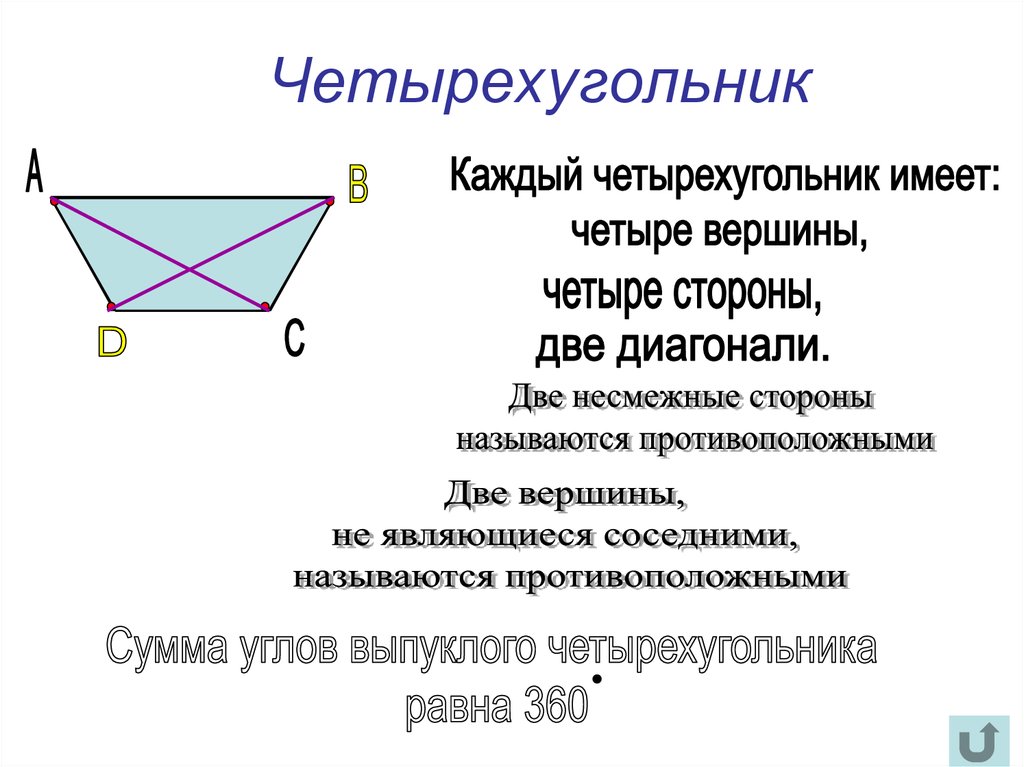
6. Четырехугольник

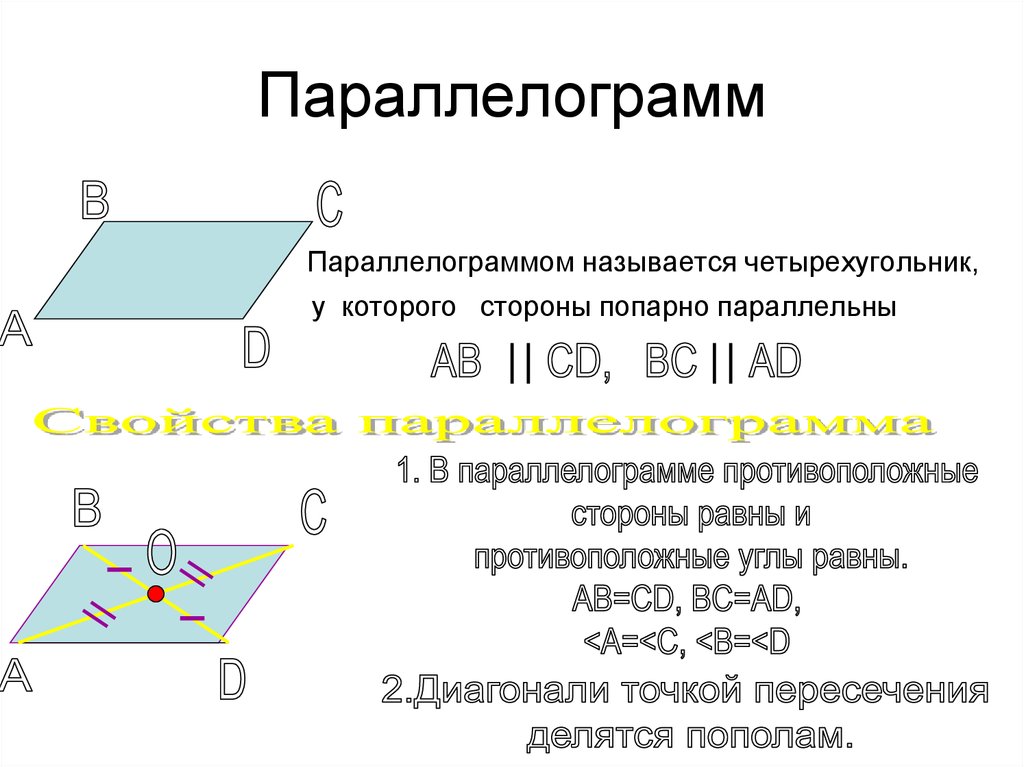
7. Параллелограмм

Параллелограммом называется четырехугольник,
у которого стороны попарно параллельны

8.

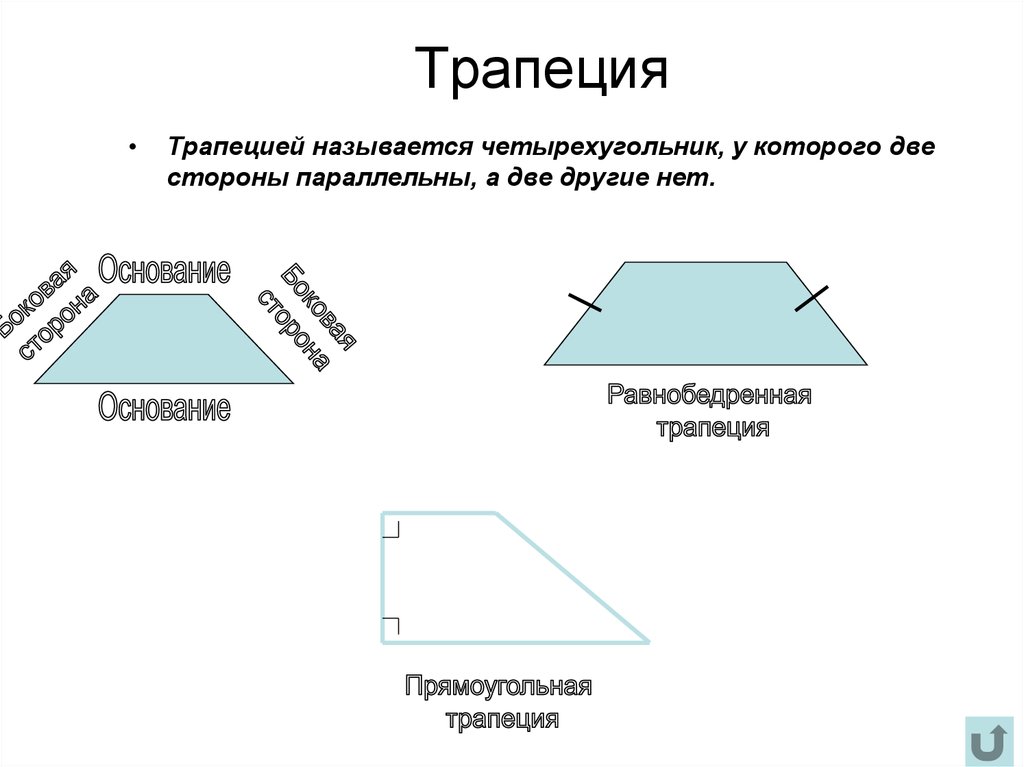
9. Трапеция

Трапецией называется четырехугольник, у которого две
стороны параллельны, а две другие нет.

10.

Если на одной из двух прямых отложены
последовательно равные отрезки и через их
концы проведены параллельные прямые,
пересекающие вторую прямую, то они отсекут на
второй прямой равные между собой отрезки.
А
А
В1
1
1
В1
А2
С
1
А2
3
В2
В2
А3
А3
4
D
В3
А4
В4
А4
2
В3
В4

11. Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы
прямые.

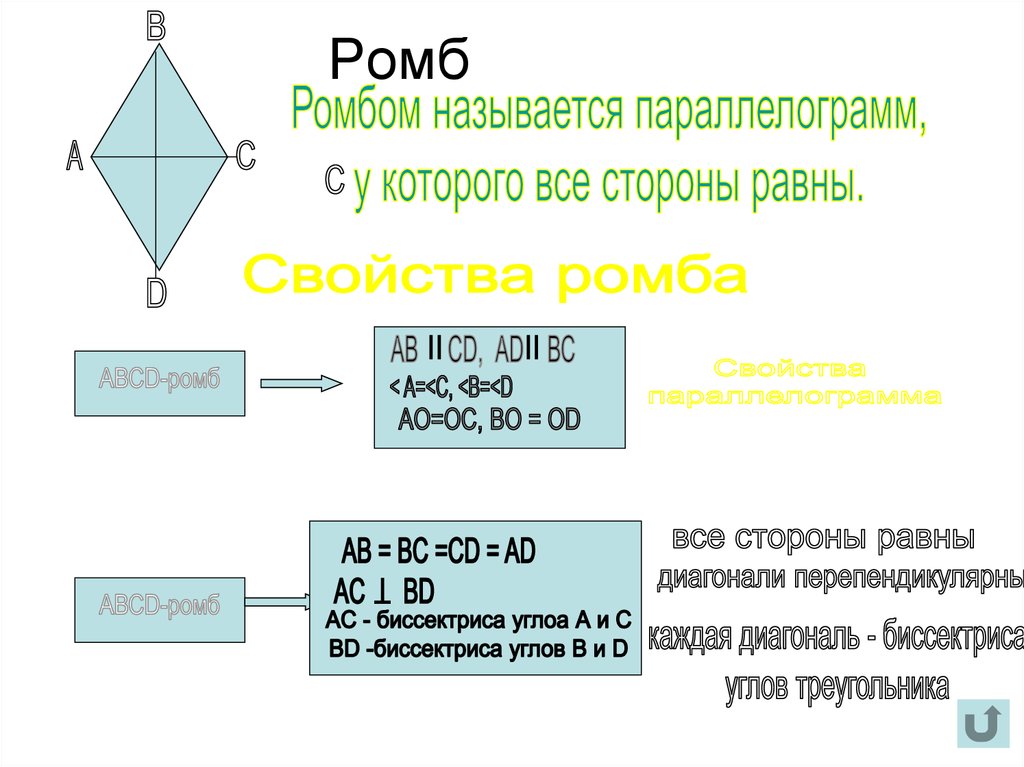
12. Ромб

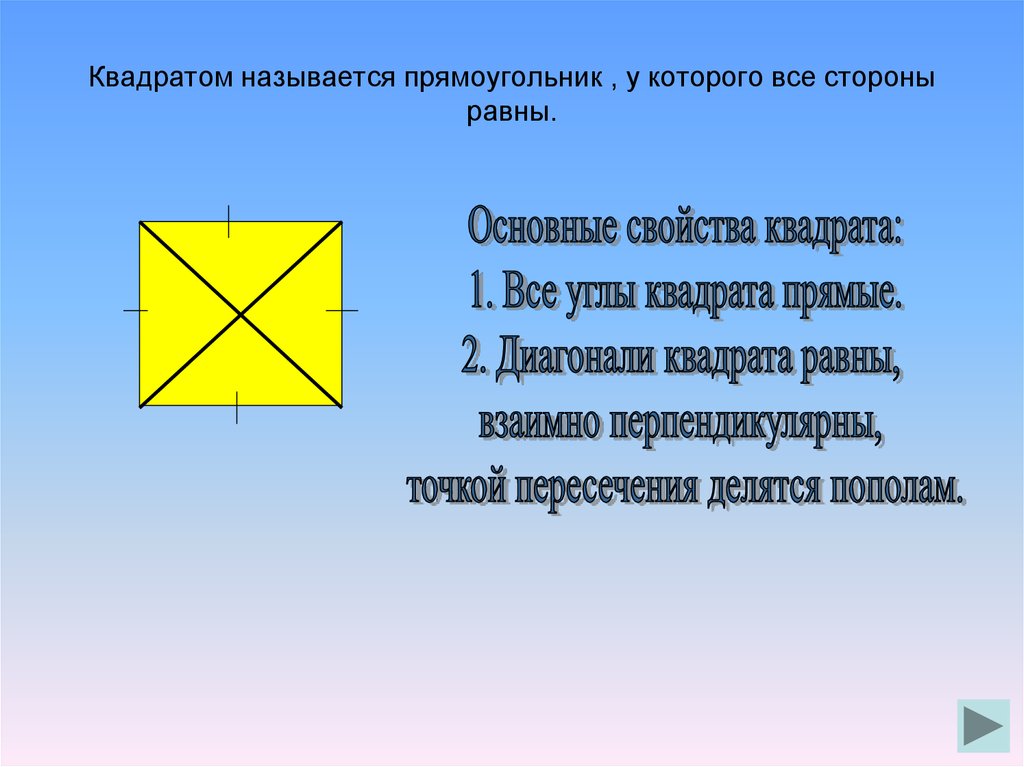
13. Квадратом называется прямоугольник , у которого все стороны равны.

14.

А
а
А1
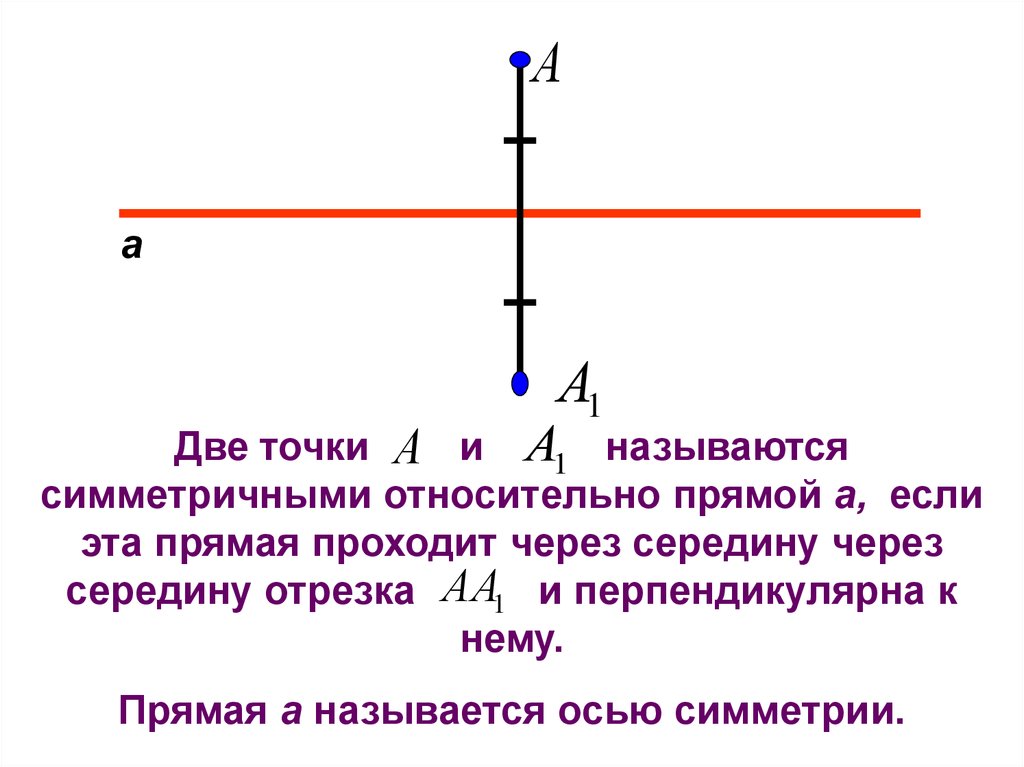
Две точки А и А1 называются
симметричными относительно прямой а, если
эта прямая проходит через середину через
середину отрезка АА1 и перпендикулярна к
нему.
Прямая а называется осью симметрии.

15.

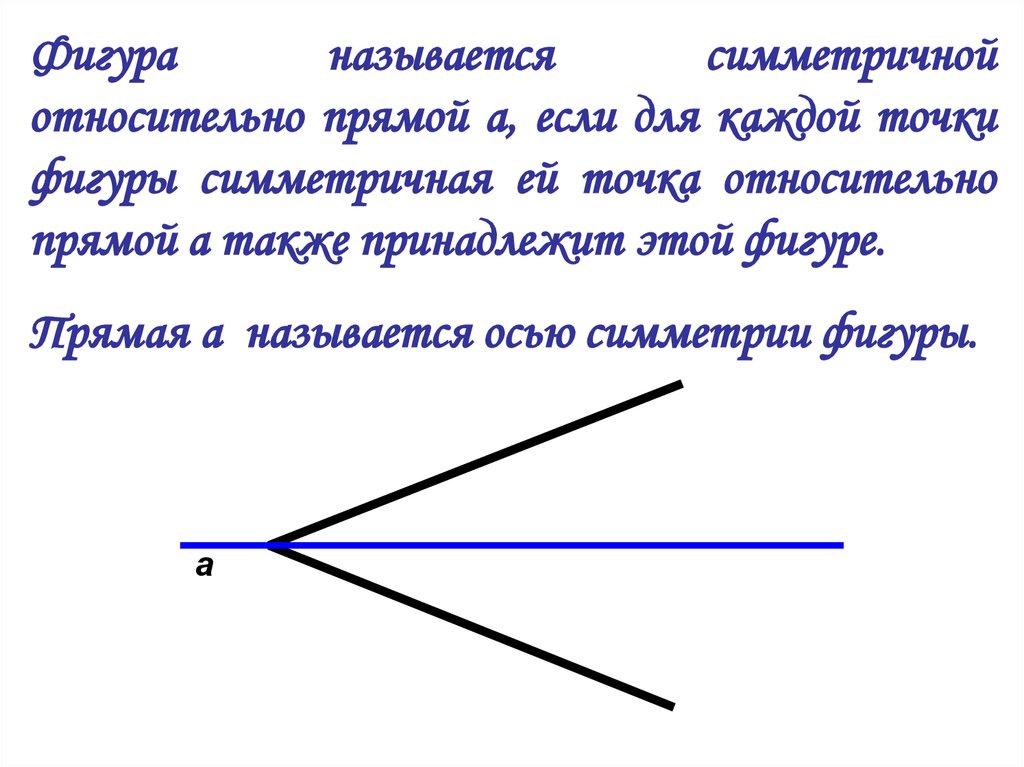
Фигура
называется
симметричной
относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно
прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
а

16.

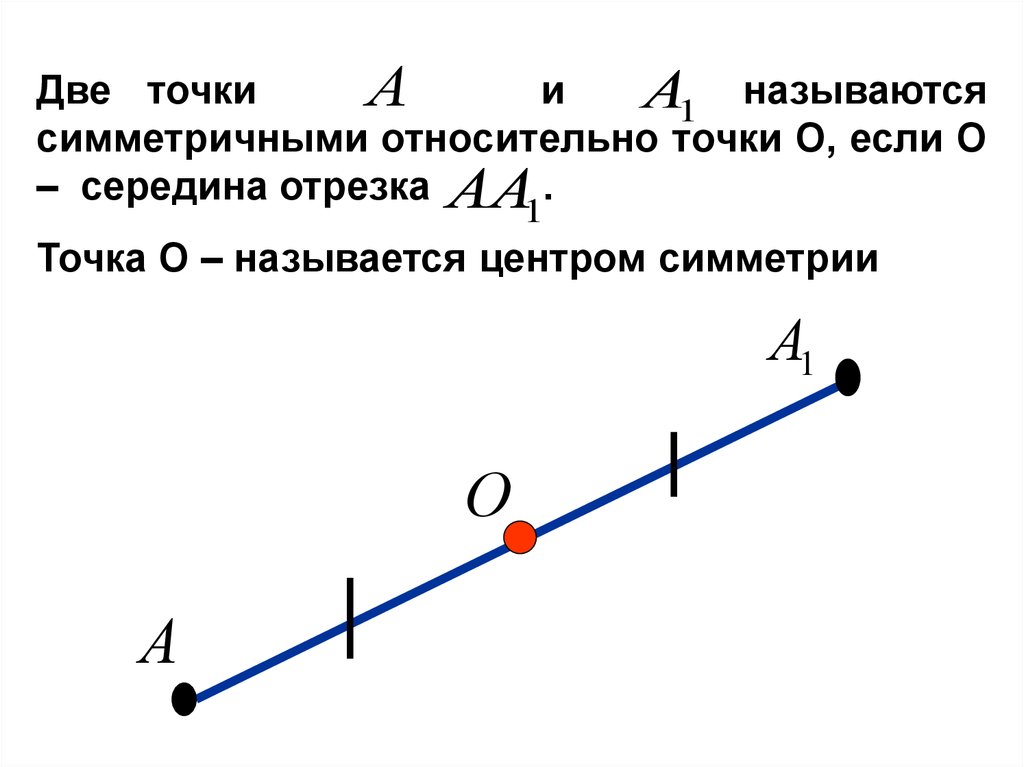
Две точки
и
А
А1 называются
симметричными относительно точки О, если О
– середина отрезка АА .
1
Точка О – называется центром симметрии
А1
О
А

17.

Фигура называется симметричной относительно
точки О, если для каждой точки фигуры
симметричная ей точка относительно точки О
также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.

18.

Происхождение науки
геометрии.
Для чего нужно было измерять площади?
Людям часто приходилось делить землю по берегам
Нила на участки. Подсчитывать площадь трудно,
берега извилисты, границы участка неровные. И люди
постепенно научились измерять такие площади,
разбивая их на прямоугольные и треугольные участки
(17 век до н. э.)

19. Понятие площади. Свойства площадей.

Площадь – положительное число, которое
показывает сколько раз единица измерения или
ее часть укладывается в данной фигуре.

20.

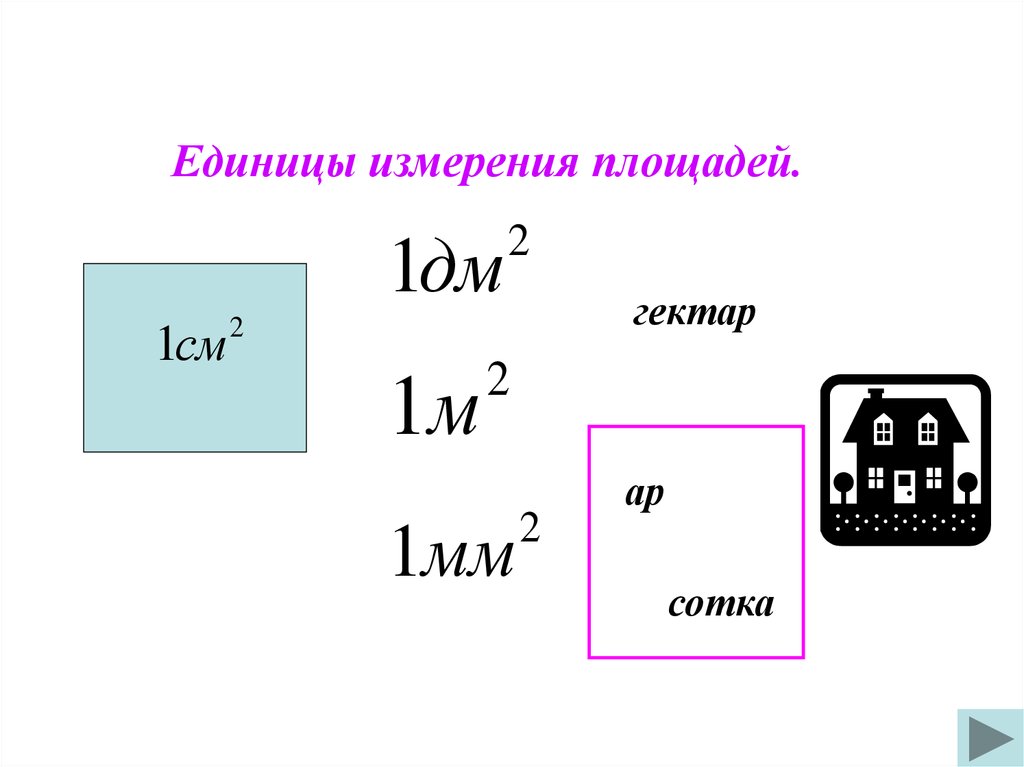
Единицы измерения площадей.
1дм
1см
2
гектар
2
1м
2
1мм
2
ар
сотка

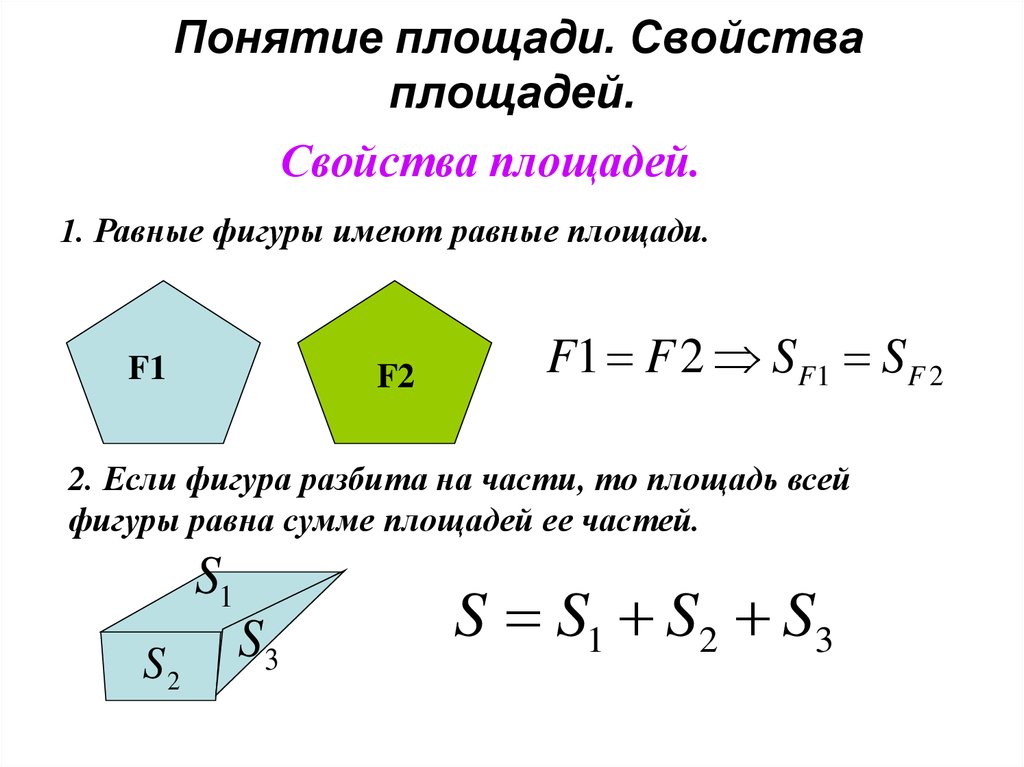
21. Понятие площади. Свойства площадей.

Свойства площадей.
1. Равные фигуры имеют равные площади.
F1
F2
F1 F 2 S F 1 S F 2
2. Если фигура разбита на части, то площадь всей
фигуры равна сумме площадей ее частей.
S1
S2
S3
S S1 S2 S3

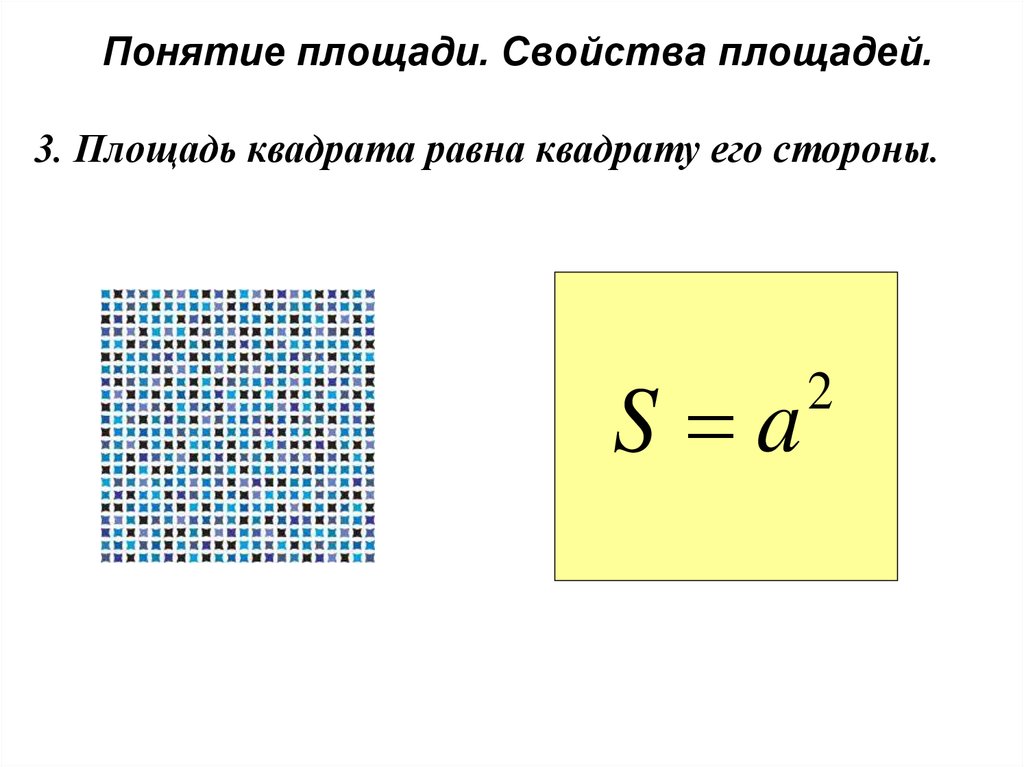
22. Понятие площади. Свойства площадей.

3. Площадь квадрата равна квадрату его стороны.
S a
2

23. Площадь прямоугольника.

Теорема.
Площадь прямоугольника равна
смежных сторон.
a
В
С
b
А
D
произведению
S ab

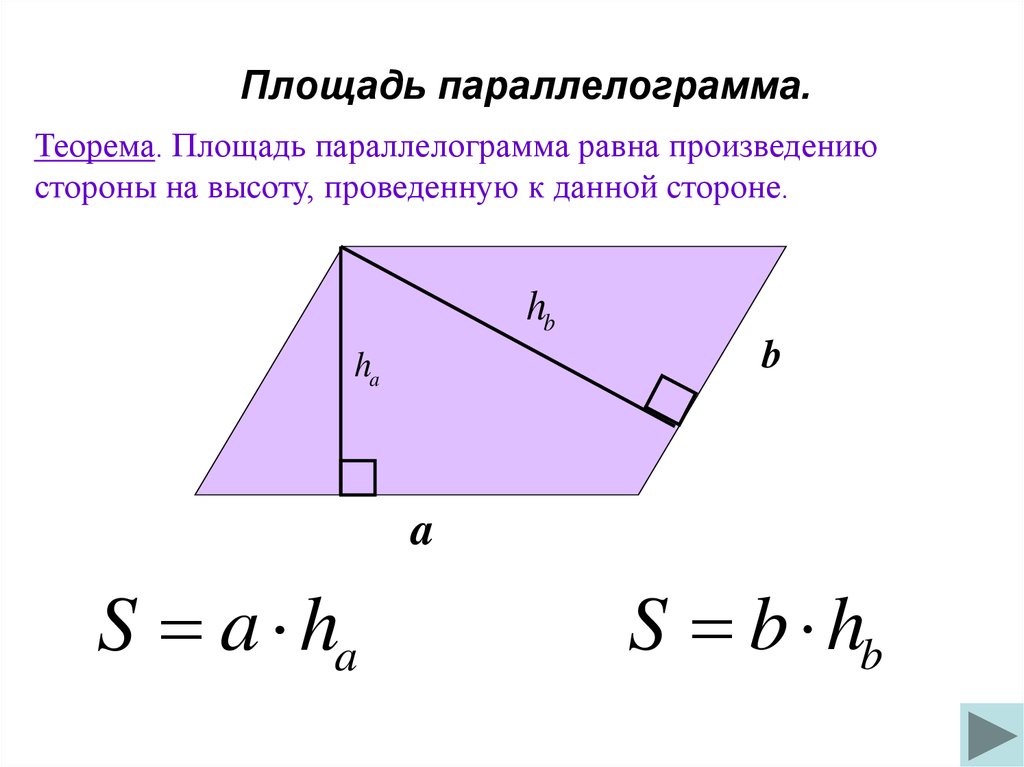
24. Площадь параллелограмма.

Теорема. Площадь параллелограмма равна произведению
стороны на высоту, проведенную к данной стороне.
hb
b
ha
a
S a ha
S b hb

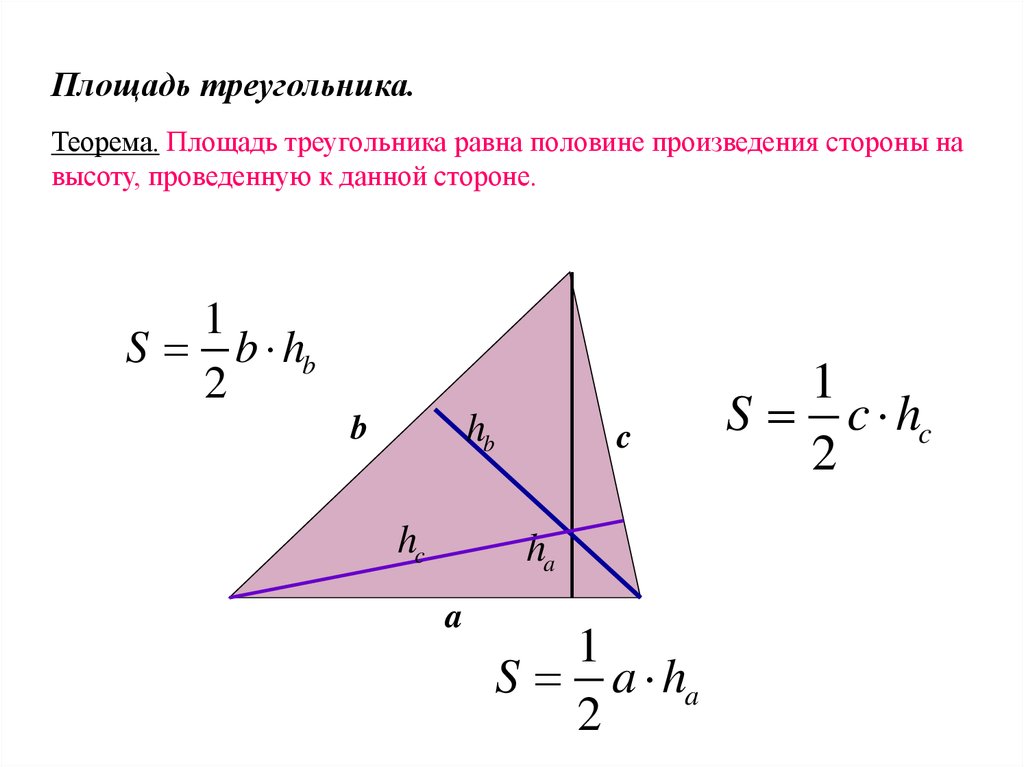
25.

Площадь треугольника.
Теорема. Площадь треугольника равна половине произведения стороны на
высоту, проведенную к данной стороне.
1
S b hb
2
hb
b
hc
c
ha
a
1
S a ha
2
1
S c hc
2

26.

Площадь треугольника. Прямоугольный треугольник.
1
S ab
2
b
а
Площадь прямоугольного
треугольника равна
половине произведения
его катетов.

27.

Площадь трапеции.
Теорема. Площадь трапеции равна произведению полусуммы
ее оснований на высоту.
b
1
S ( a b) h
2
h
а

28.

В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов.
c²=a²+b²
С – гипотенуза
a,b – катеты.

29. Определение подобных треугольников

В
А
С
B1
A1
C1
AB и A1B1, BC и B1C1, AC и
A1C1 – сходственные стороны
Два треугольника
называются подобными,
если их углы
соответственно равны и
стороны одного
треугольника
пропорциональны
сходственным сторонам
другого треугольника.

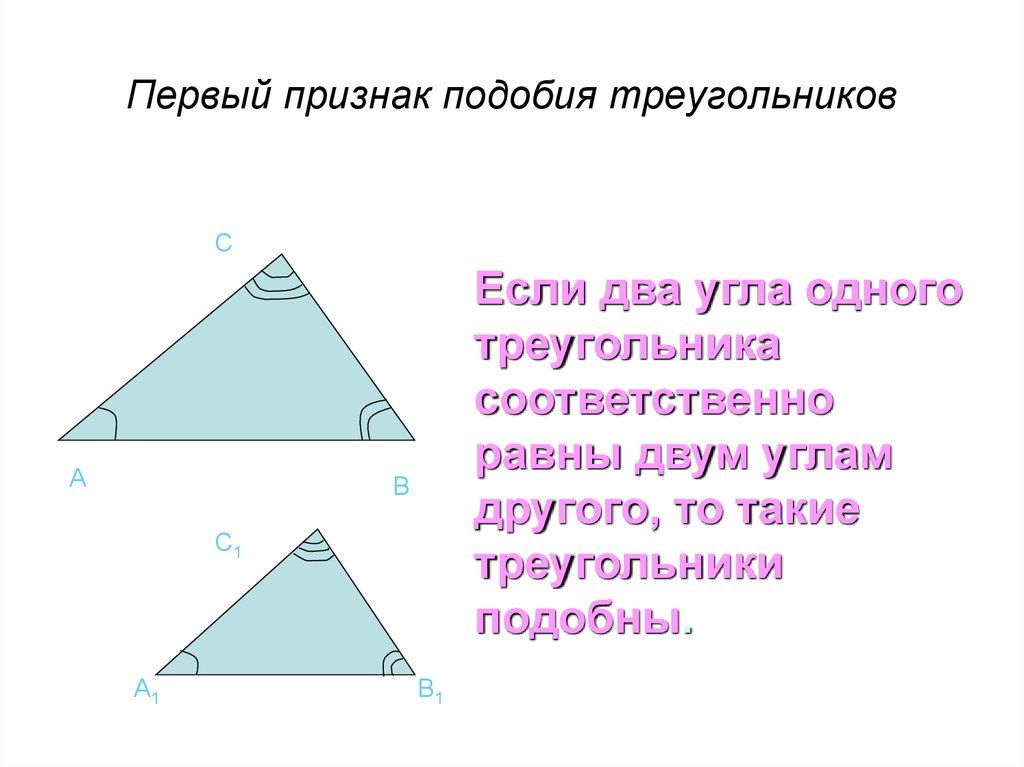
30. Первый признак подобия треугольников

C
A
Если два угла одного
треугольника
соответственно
равны двум углам
другого, то такие
треугольники
подобны.
B
C1
A1
B1

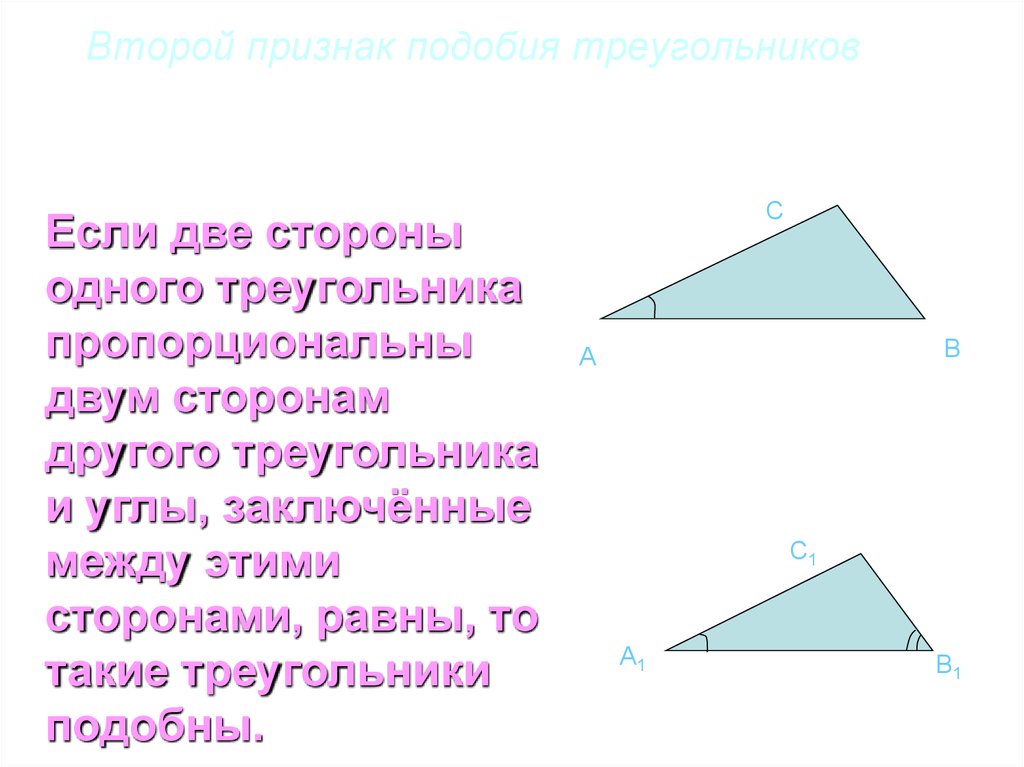
31. Второй признак подобия треугольников

Если две стороны
одного треугольника
пропорциональны
двум сторонам
другого треугольника
и углы, заключённые
между этими
сторонами, равны, то
такие треугольники
подобны.
C
B
A
C1
A1
B1

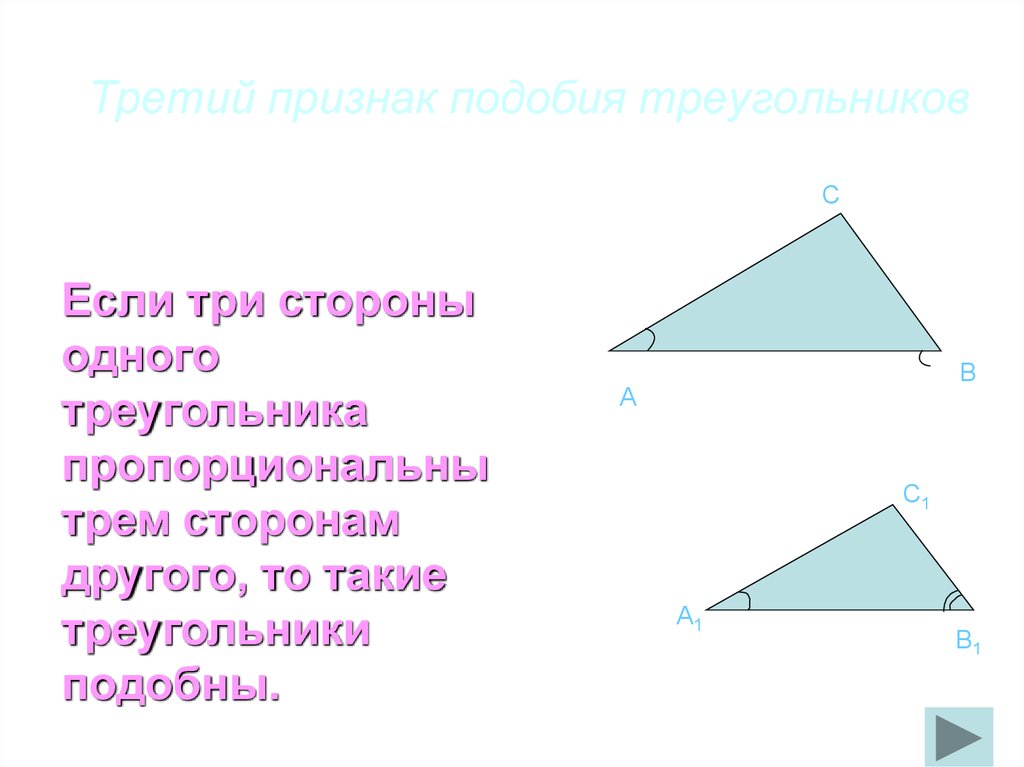
32. Третий признак подобия треугольников

C
Если три стороны
одного
треугольника
пропорциональны
трем сторонам
другого, то такие
треугольники
подобны.
B
A
C1
A1
B1

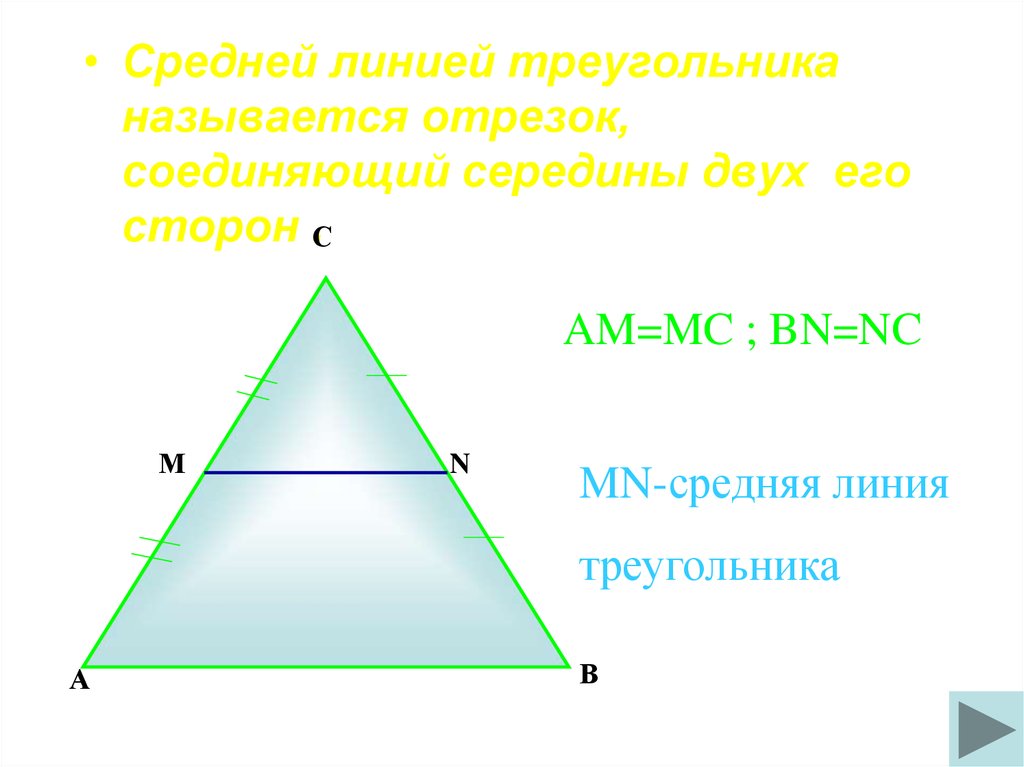
33.

• Средней линией треугольника
называется отрезок,
соединяющий середины двух его
сторон .С
AM=MC ; BN=NC
М
N
MN-средняя линия
треугольника
А
В

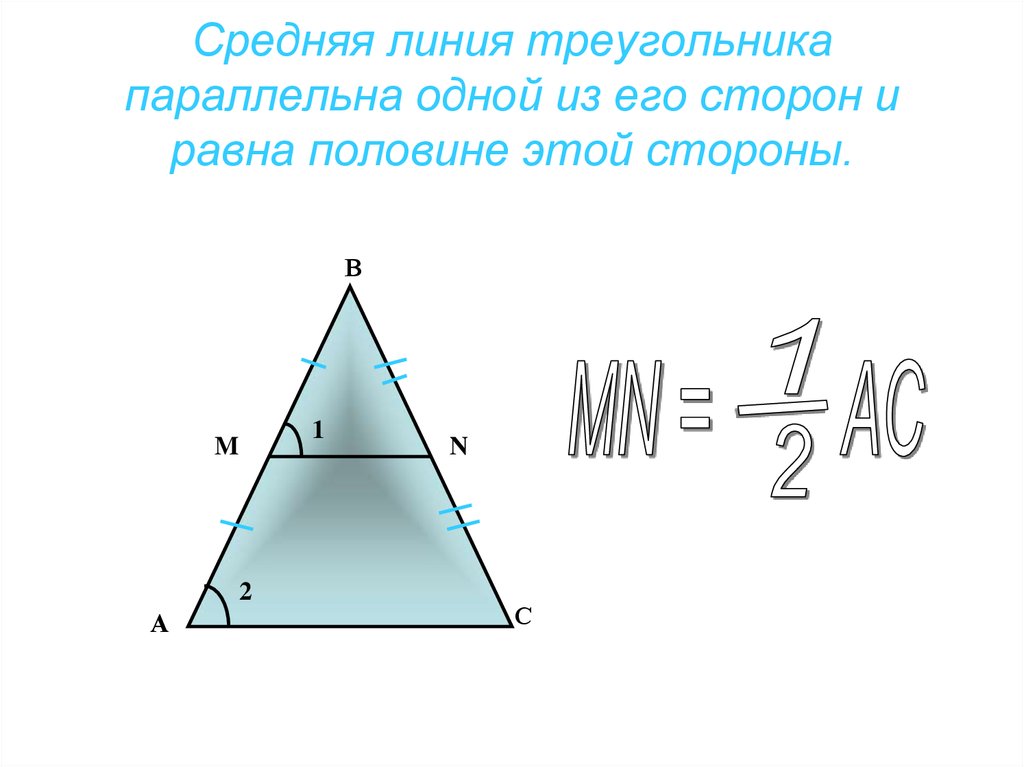
34. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

В
M
2
А
1
N
С

35.

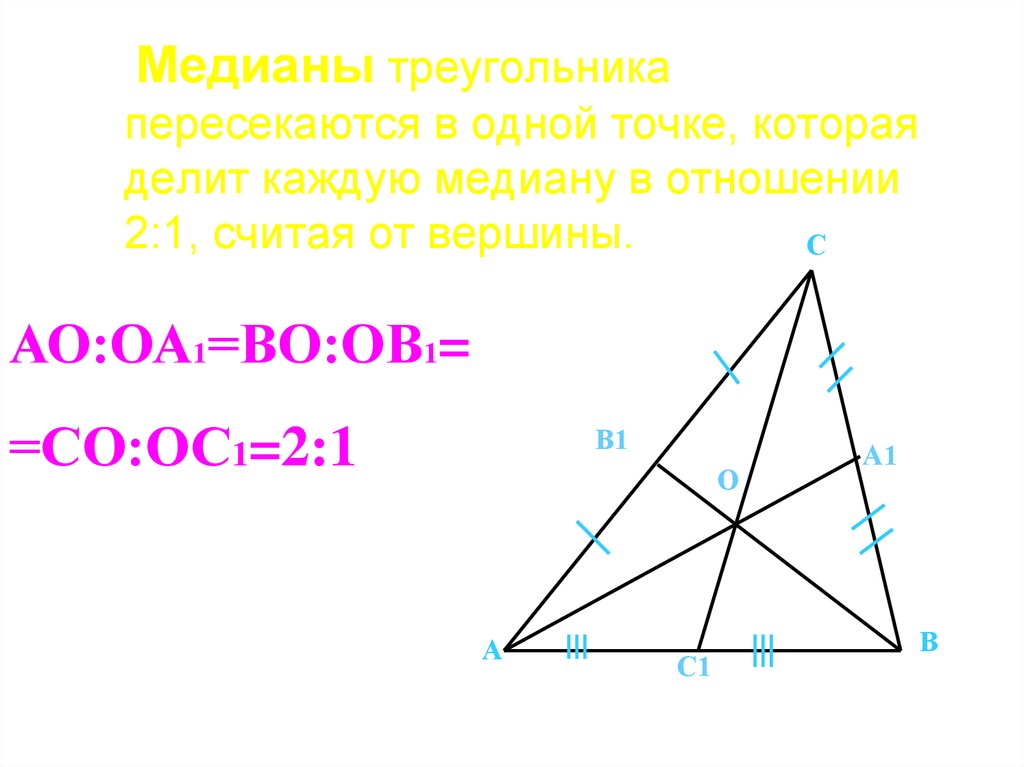
Медианы треугольника
пересекаются в одной точке, которая
делит каждую медиану в отношении
2:1, считая от вершины.
С
АО:ОА1=ВО:ОВ1=
=СО:ОС1=2:1
В1
О
А
С1
А1
В

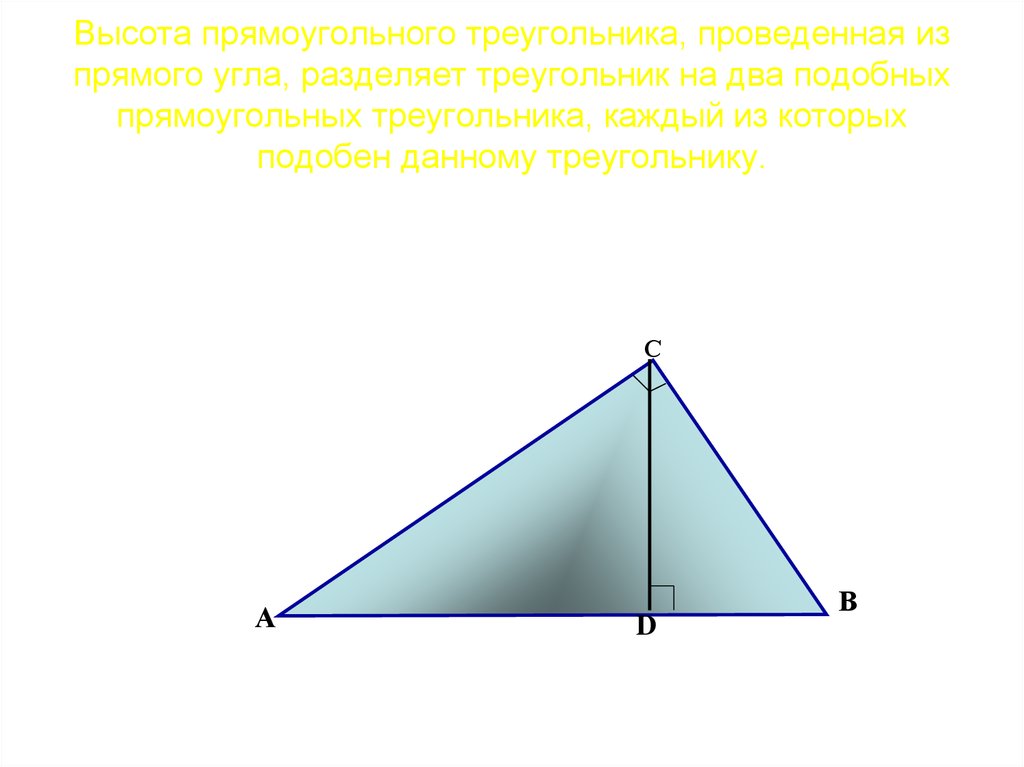
36. Высота прямоугольного треугольника, проведенная из прямого угла, разделяет треугольник на два подобных прямоугольных

треугольника, каждый из которых
подобен данному треугольнику.
С
А
D
В

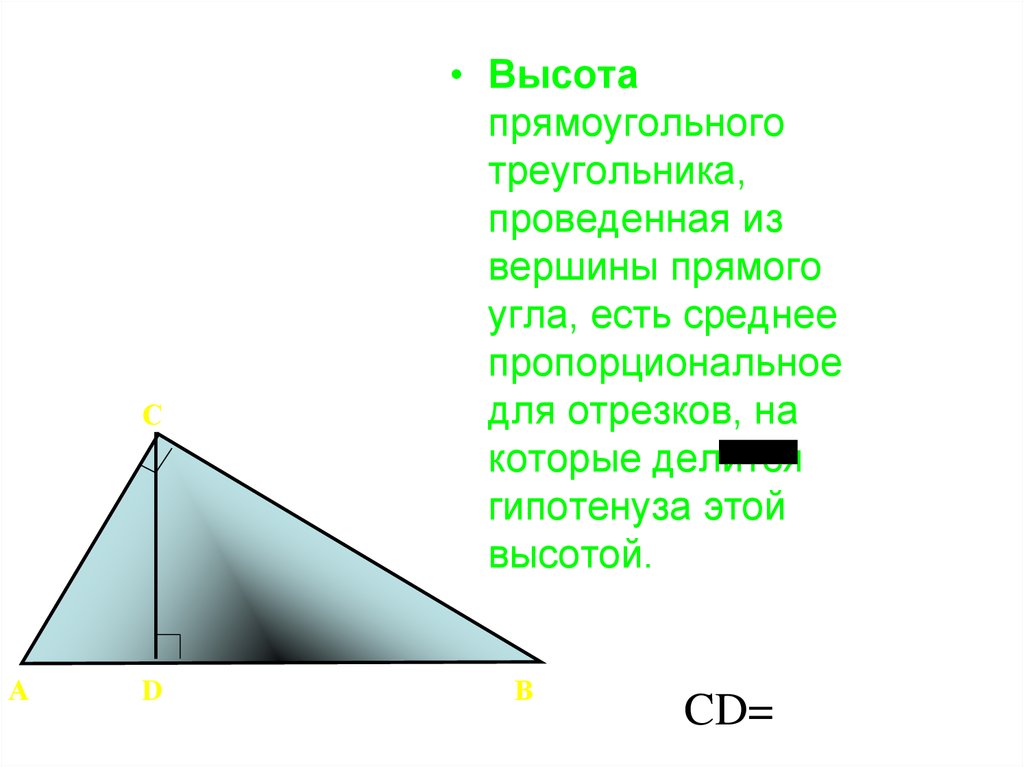
37.

С
А
D
• Высота
прямоугольного
треугольника,
проведенная из
вершины прямого
угла, есть среднее
пропорциональное
для отрезков, на
AD * DB
которые делится
гипотенуза этой
высотой.
В
CD=

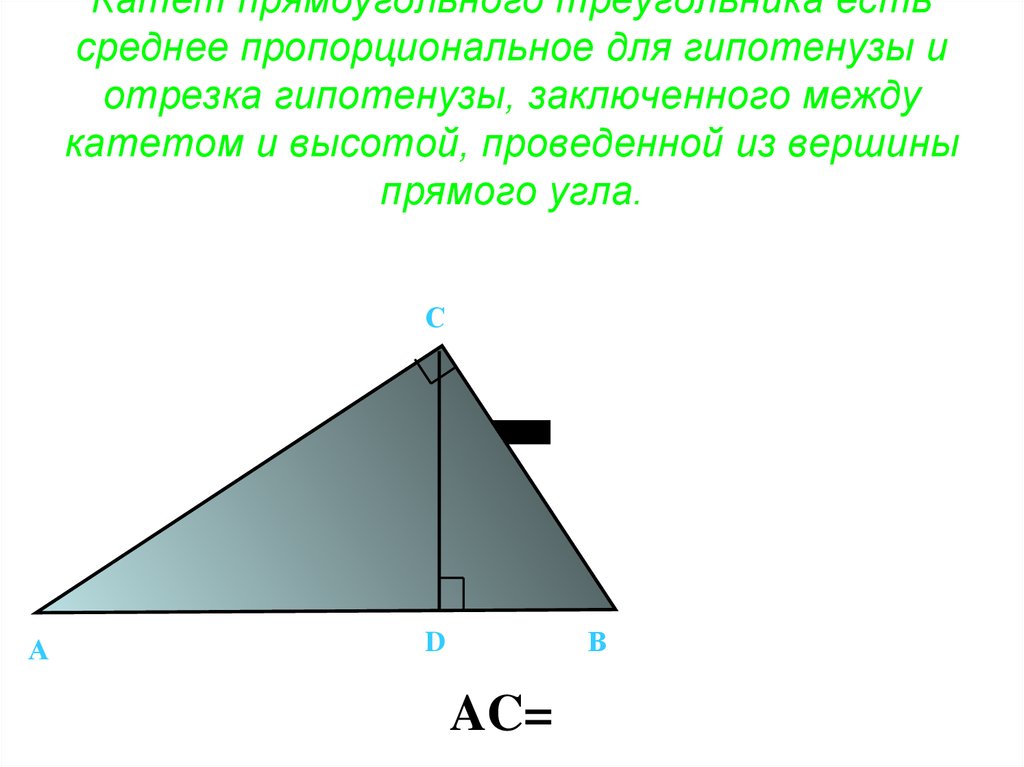
38. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом

и высотой, проведенной из вершины
прямого угла.
С
AB* AD
А
В
D
AC=

39. Соотношения между сторонами и углами прямоугольного треугольника

А
В
С

40.

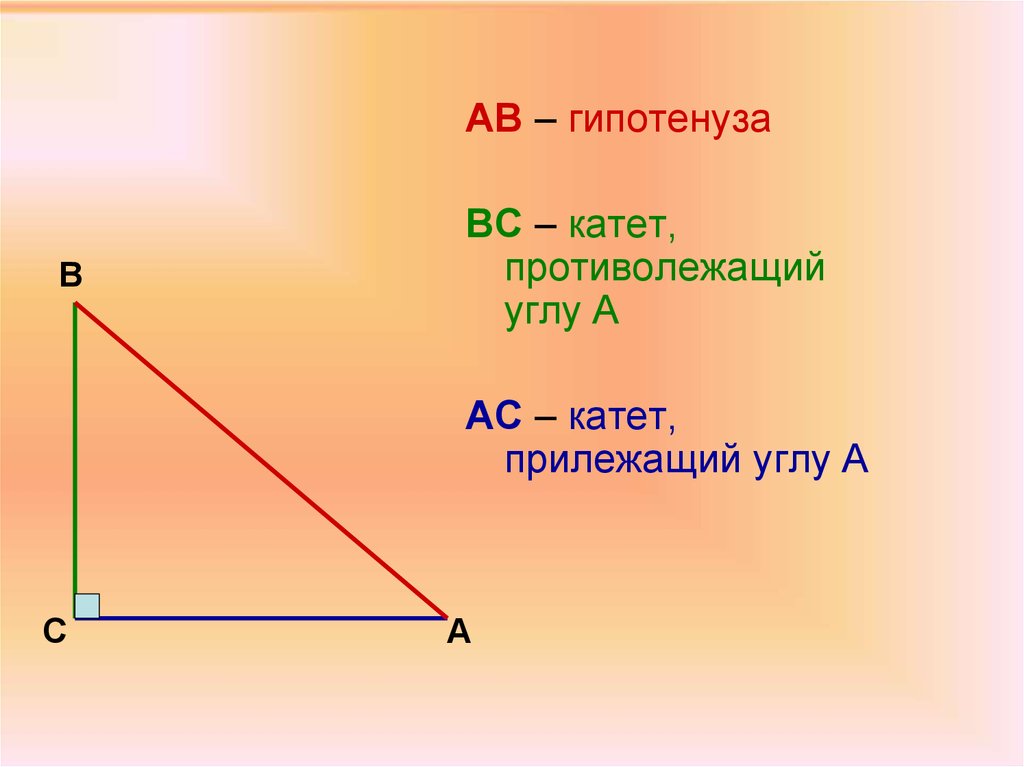
АВ – гипотенуза
В
ВС – катет,
противолежащий
углу А
АС – катет,
прилежащий углу А
С
А

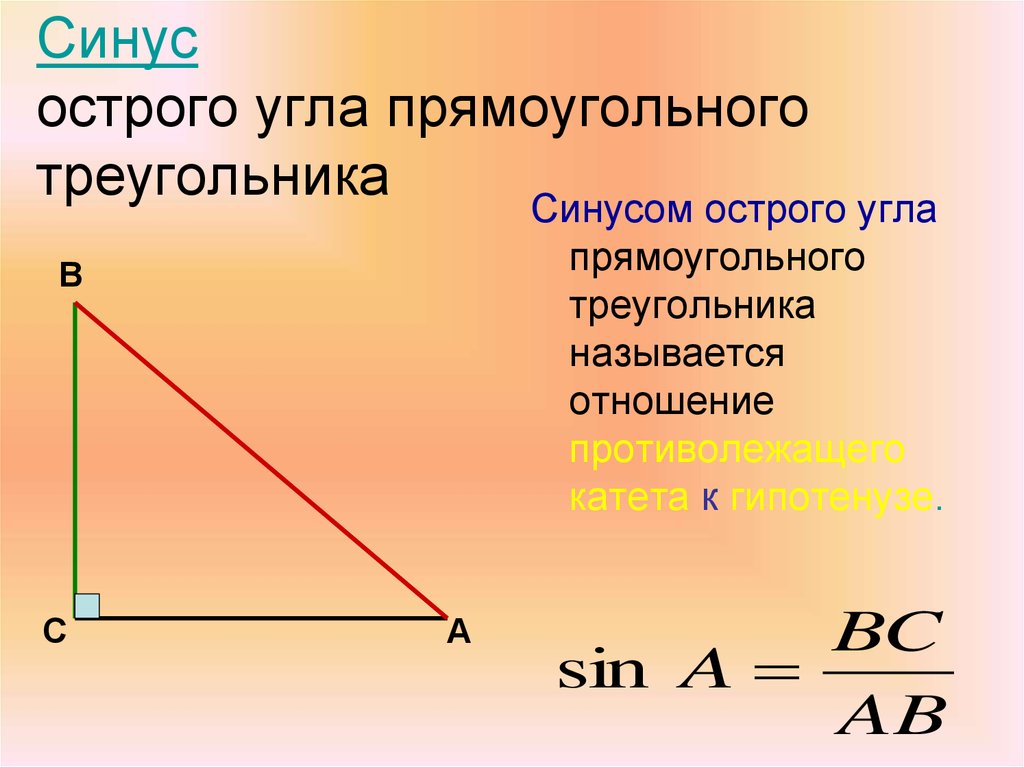
41. Синус острого угла прямоугольного треугольника

Синусом острого угла
прямоугольного
треугольника
называется
отношение
противолежащего
катета к гипотенузе.
В
С
А
BC
sin A
AB

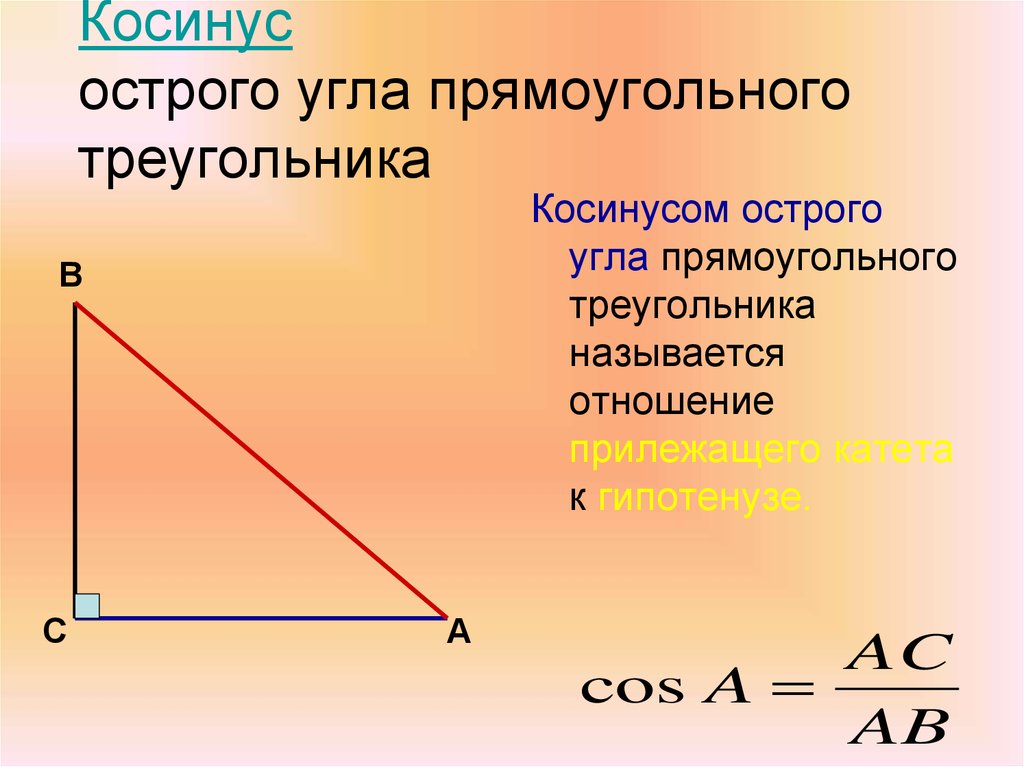
42. Косинус острого угла прямоугольного треугольника

Косинусом острого
угла прямоугольного
треугольника
называется
отношение
прилежащего катета
к гипотенузе.
В
С
А
AC
cos A
AB

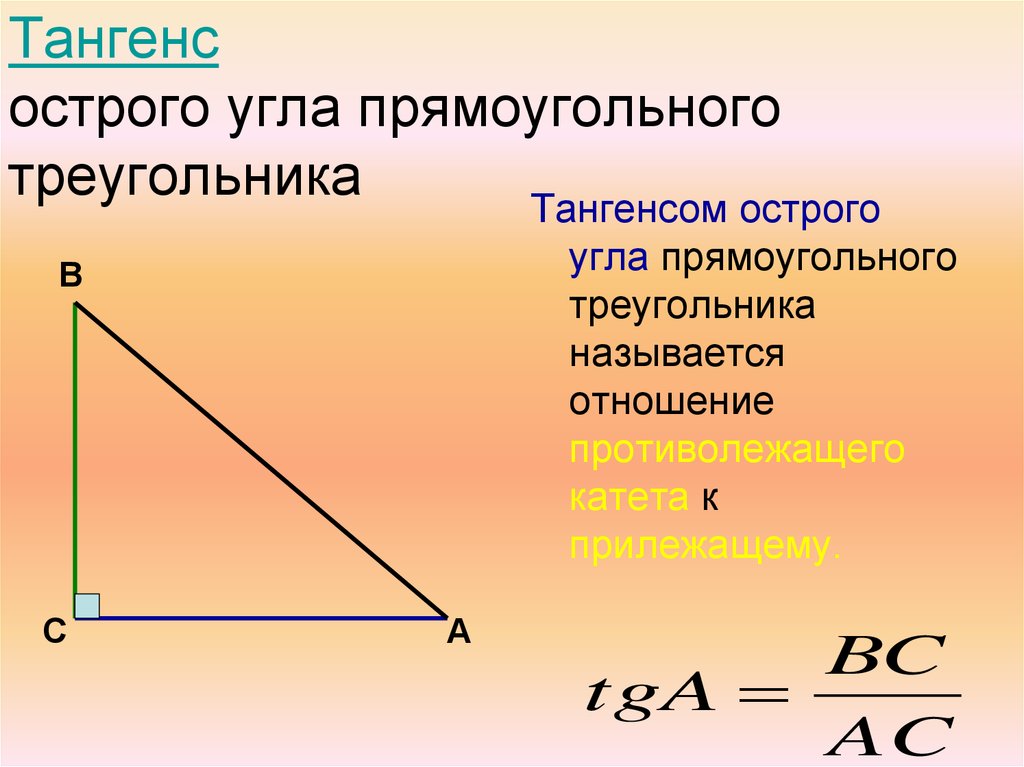
43. Тангенс острого угла прямоугольного треугольника

Тангенсом острого
угла прямоугольного
треугольника
называется
отношение
противолежащего
катета к
прилежащему.
В
С
А
BC
tgA
AC

44. Тригонометрические тождества

1) Основное тригонометрическое
тождество:
sin A cos A 1
2
2
2) Тангенс угла равен отношению
синуса к косинусу этого угла.
sin A
tgA
cos A

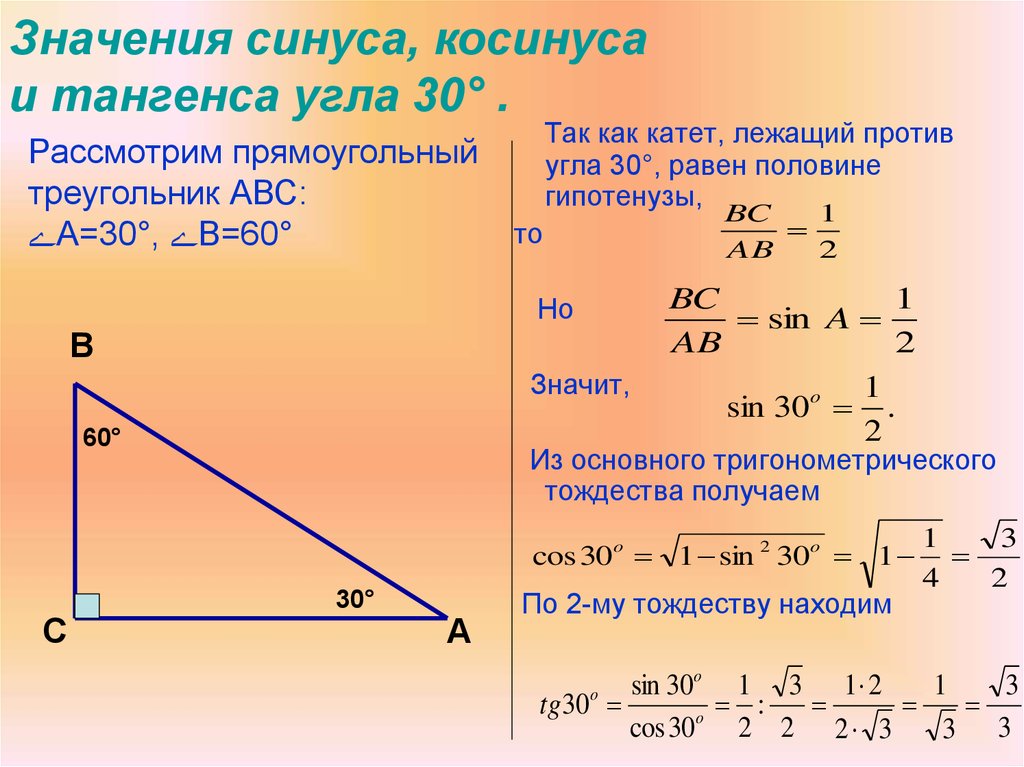
45. Значения синуса, косинуса и тангенса угла 30° .

Рассмотрим прямоугольный
треугольник АВС:
‫ ‬А=30°, ‫ ‬В=60°
Так как катет, лежащий против
угла 30°, равен половине
гипотенузы,
BC
1
AB
2
то
Но
В
Значит,
60°
BC
1
sin A
AB
2
1
o
sin 30 .
2
Из основного тригонометрического
тождества получаем
cos 30o 1 sin 2 30o 1
С
30°
А
По 2-му тождеству находим
1
3
4
2
sin 30o 1 3 1 2
1
3
tg30
:
o
cos 30 2 2 2 3
3 3
o

46. Значения синуса, косинуса и тангенса угла 60°.

Так как катет, лежащий против
Рассмотрим прямоугольный
угла 30°, равен половине
треугольник АВС:
гипотенузы,
BC
1
то
‫ ‬А=30°, ‫ ‬В=60°
AB
2
Или
В
BC
1
cos B
AB
2
Значит,
1
cos 60
2
Из основного
тригонометрического тождества
получаем
60°
o
sin 60o 1 cos 2 60o 1
С
30°
А
1
3
4
2
По 2-му тождеству находим
sin 60o
3 1
3 2
tg 60
:
3
o
cos 60
2 2
2 1
o

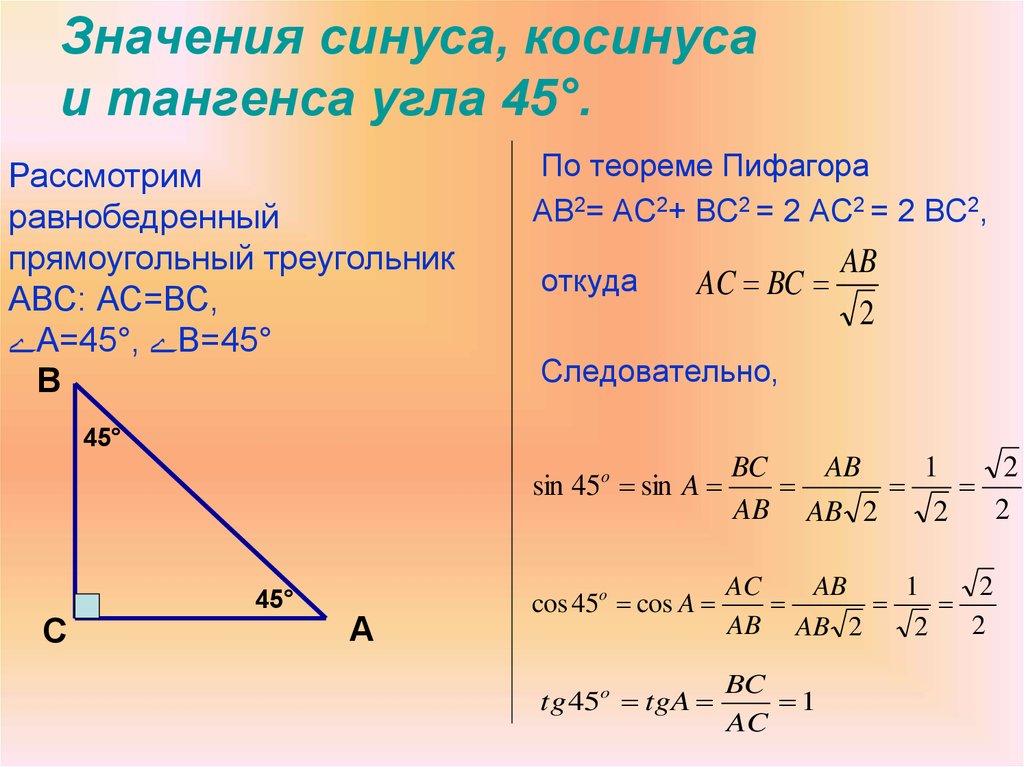
47. Значения синуса, косинуса и тангенса угла 45°.

Рассмотрим
равнобедренный
прямоугольный треугольник
АВС: АС=ВС,
‫ ‬А=45°, ‫ ‬В=45°
В
По теореме Пифагора
АВ2= АС2+ ВС2 = 2 АС2 = 2 ВС2,
откуда
AB
AC BC
2
Следовательно,
45°
BC
AB
1
2
sin 45 sin A
AB AB 2
2
2
o
С
45°
А
cos 45o cos A
tg 45o tgA
AC
AB
1
2
AB AB 2
2
2
BC
1
AC