Синус, косинус и тангенс острого угла прямоугольного треугольника

1. Синус, косинус и тангенс острого угла прямоугольного треугольника

2. Синус, косинус и тангенс острого угла прямоугольного треугольника

Форма урока: Урок изучения нового.
Цели урока:
1.Познакомить учащихся с определениями
тригонометрических функций в прямоугольном
треугольнике и учить вычислять значения;
2.Формировать навыки написания конспекта;
3.Воспитывать наблюдательность, развивать память,
продолжить работу над формированием системы
знаний .

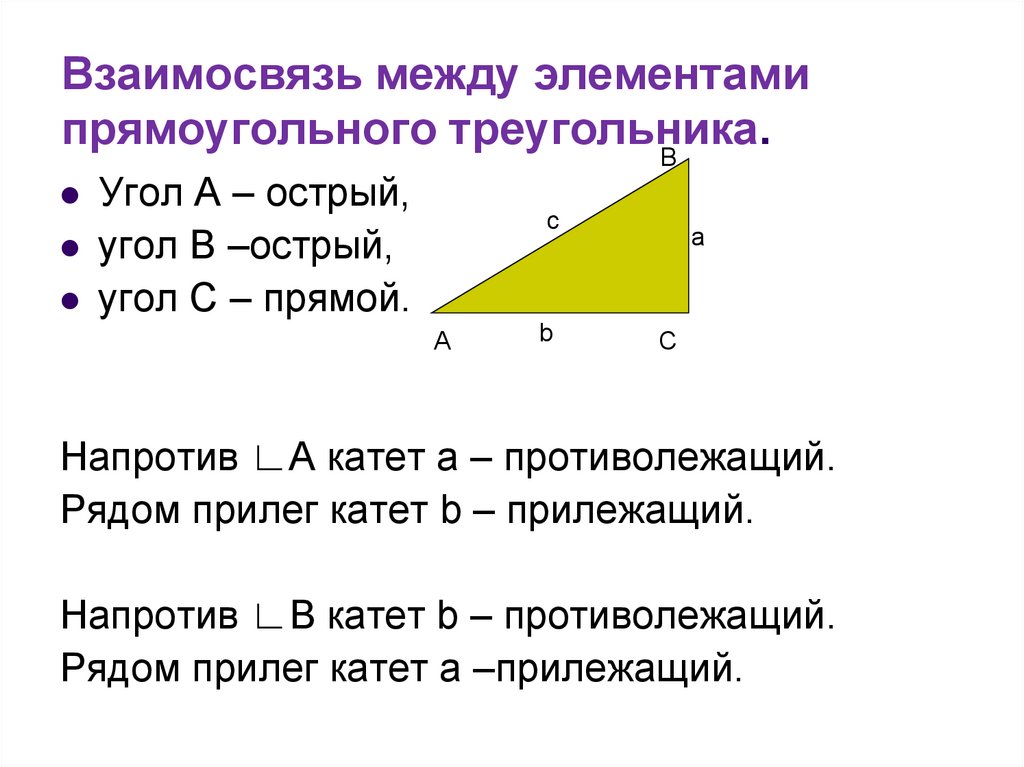
3. Взаимосвязь между элементами прямоугольного треугольника.

В
Угол А – острый,
угол В –острый,
угол С – прямой.
с
А
b
а
С
Напротив ∟А катет а – противолежащий.
Рядом прилег катет b – прилежащий.
Напротив ∟В катет b – противолежащий.
Рядом прилег катет а –прилежащий.

4. Взаимосвязь между элементами прямоугольного треугольника.

М
Назовите гипотенузу,
катет противолежащий углу М,
катет прилежащий углу М
катет прилежащий углу К
Катет прилежащий углу Р
Катет противолежащий углу К
Р
К

5.

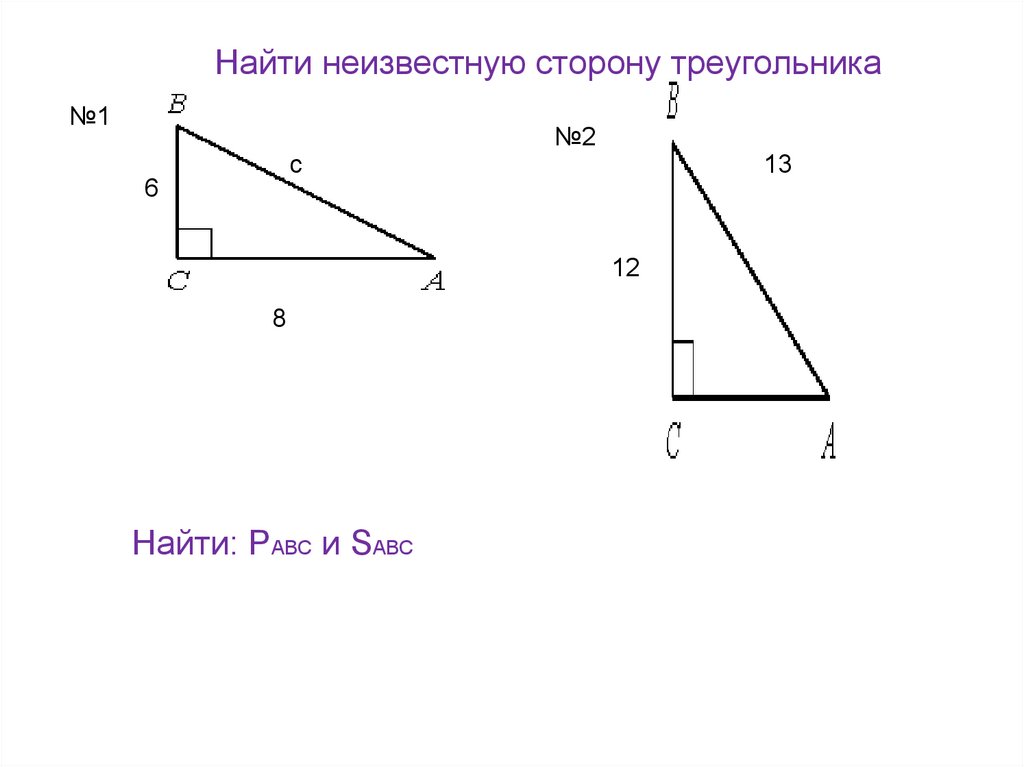
Найти неизвестную сторону треугольника
№1
с
№2
13
6
12
8
Найти: РАВС и SАВС

6. Задачи ОГЭ-2016 с прямоугольным треугольником

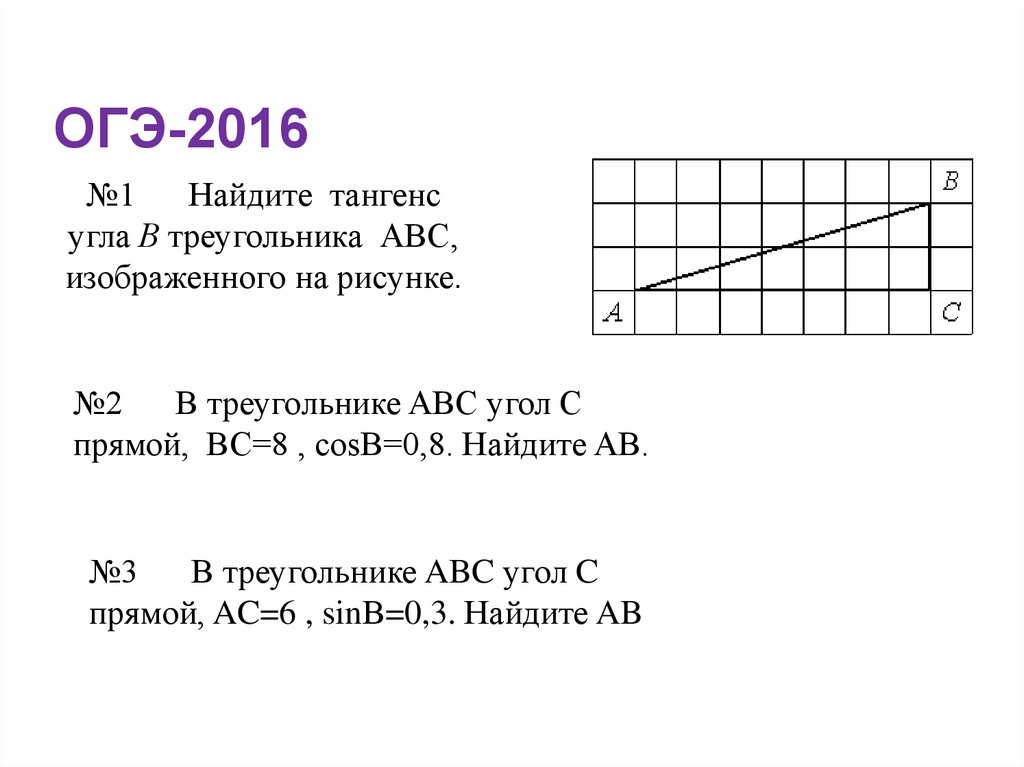
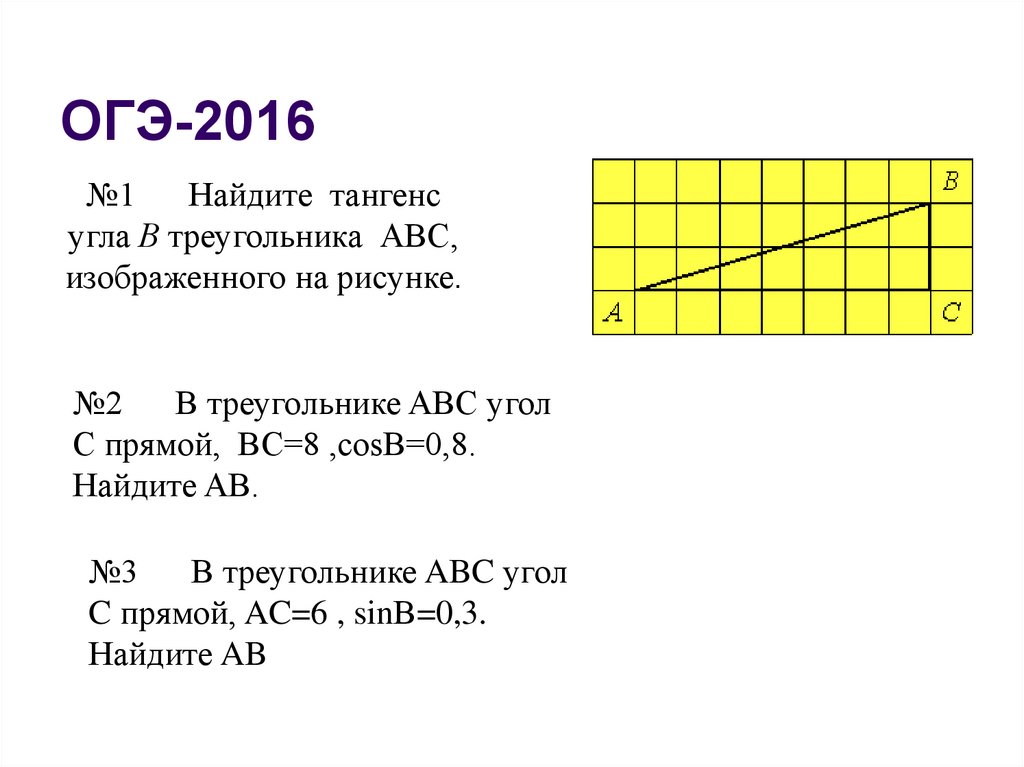
7. ОГЭ-2016

№1
Найдите тангенс
угла В треугольника АВС,
изображенного на рисунке.
№2
В треугольнике ABC угол C
прямой, BC=8 , сosB=0,8. Найдите AB.
№3
В треугольнике ABC угол C
прямой, AC=6 , sinВ=0,3. Найдите AB

8.

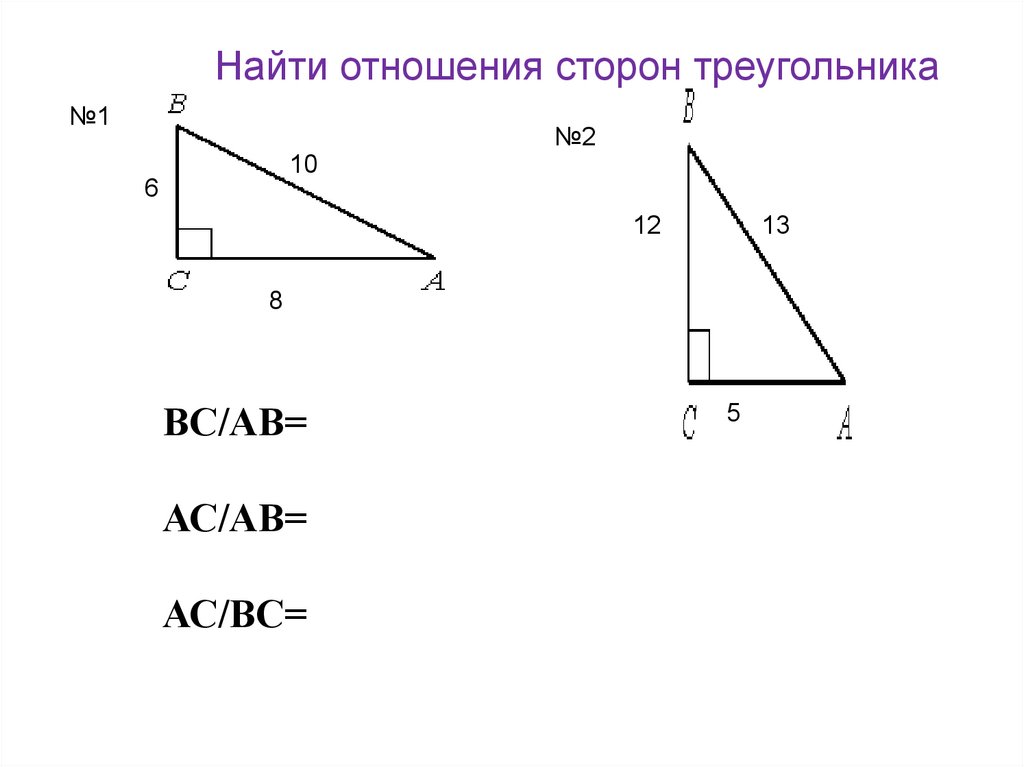
Найти отношения сторон треугольника
№1
№2
10
6
12
13
8
ВС/АВ=
АС/АВ=
АС/ВС=
5

9. Синус, косинус и тангенс острого угла прямоугольного треугольника

10. Определения:

Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему

11. Стихотворение поможет запомнить определения

«Коль не знаешь правил – минус.
Если знаешь – тебе плюс!
Если «О», то будет синус,
Если «И», то косинус.

12. Соотнесите слова стихотворения с данным определением.

Противолежащий катет
Синус А =
гипотенуза
Прилежащий катет
Косинус А =
гипотенуза
«Коль не знаешь правил –
минус.
Если знаешь – тебе плюс!
Если «О», то будет синус,
Если «И», то косинус.

13.

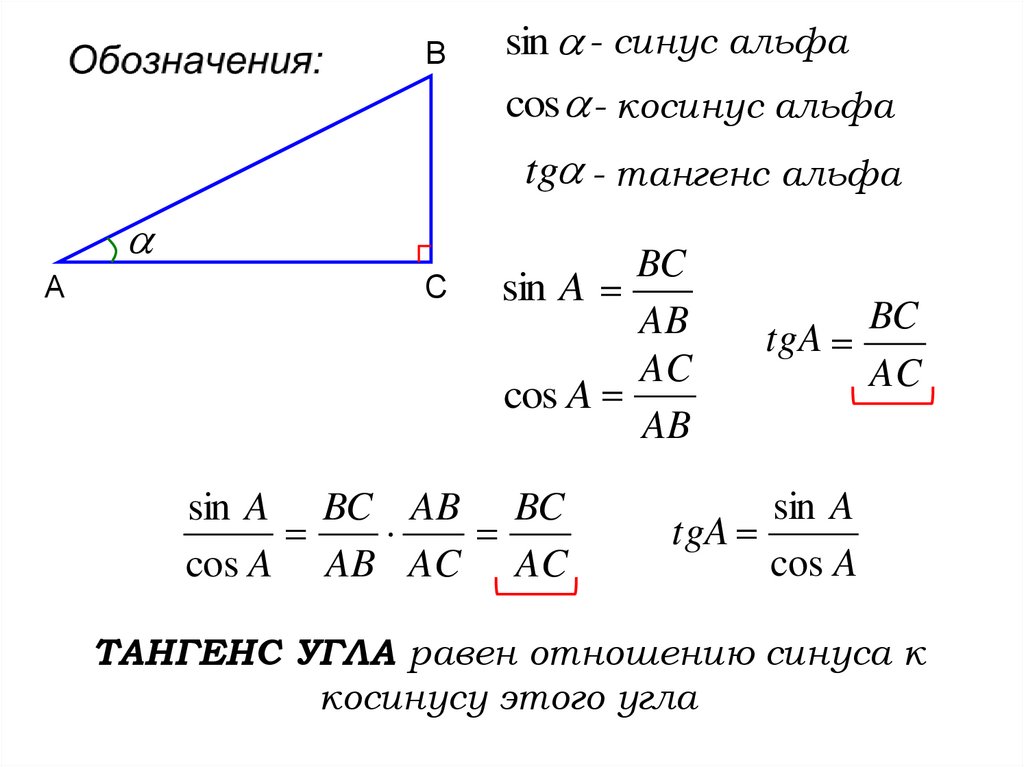
В
sin - синус альфа
cos - косинус альфа
tg - тангенс альфа
А
С
BC
sin A
AB
AC
cos A
AB
sin A BC AB BC
cos A AB AC AC
BC
tgA
AC
sin A
tgA
cos A
ТАНГЕНС УГЛА равен отношению синуса к
косинусу этого угла

14. Вывод:

Острый угол прямоугольного треугольника
зависит от гипотенузы, от катетов.
Примечание:
«Зная длины сторон прямоугольного
треугольника можно вычислить его острый
угол. Но для этого надо знать
тригонометрические функции: «синус»,
«косинус»,»тангенс»

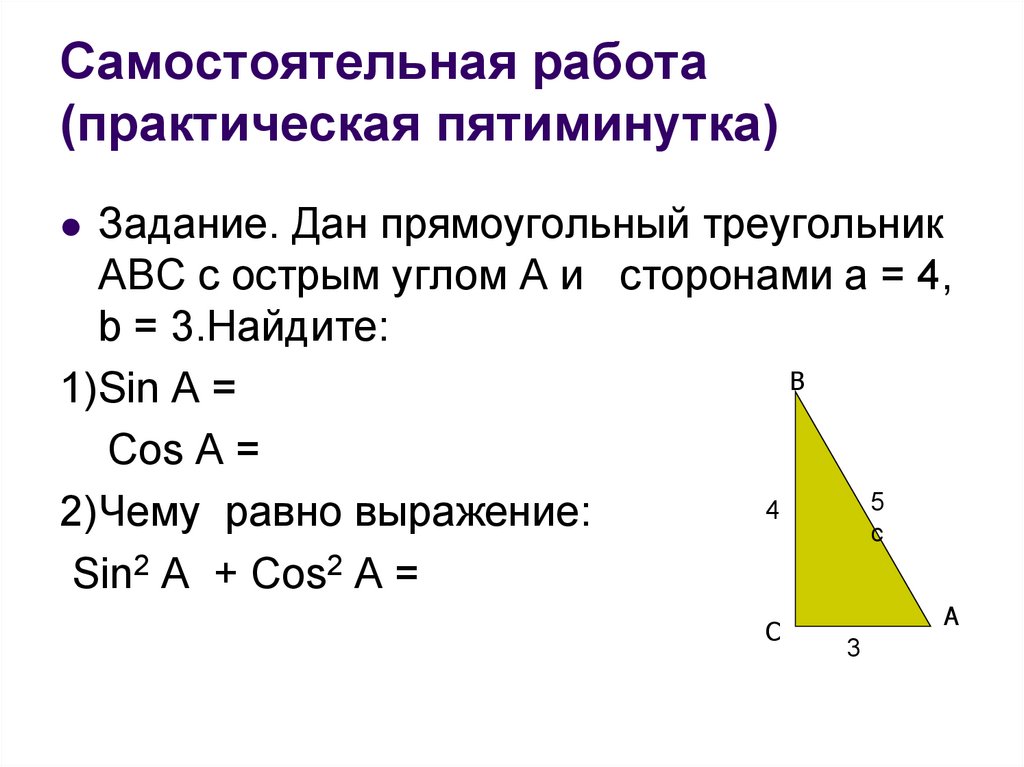
15. Самостоятельная работа (практическая пятиминутка)

Задание. Дан прямоугольный треугольник
АВС с острым углом А и сторонами а = 4,
b = 3.Найдите:
В
1)Sin A =
Cos A =
5
4
2)Чему равно выражение:
c
Sin2 A + Cos2 A =
С
А
3

16. Всегда ли это равенство верное?

1. Ответ: Sin A = 4/5
Cos A = 3/5.
2. Ответ: Sin2 A + Cos2 A = 1.
Всегда ли это равенство верное?

17. Основное тригонометрическое тождество

«Тригонометрия» в переводе с греческого«измерение треугольников»
№593(в)

18. Домашнее задание.

Пункт 66, выучить определения и
основное тригонометрическое тождество.
Решить №591(а,б), №593 (а,б)

19. ОГЭ-2016

№1
Найдите тангенс
угла В треугольника АВС,
изображенного на рисунке.
№2
В треугольнике ABC угол
C прямой, BC=8 ,сosB=0,8.
Найдите AB.
№3
В треугольнике ABC угол
C прямой, AC=6 , sinВ=0,3.
Найдите AB

20.

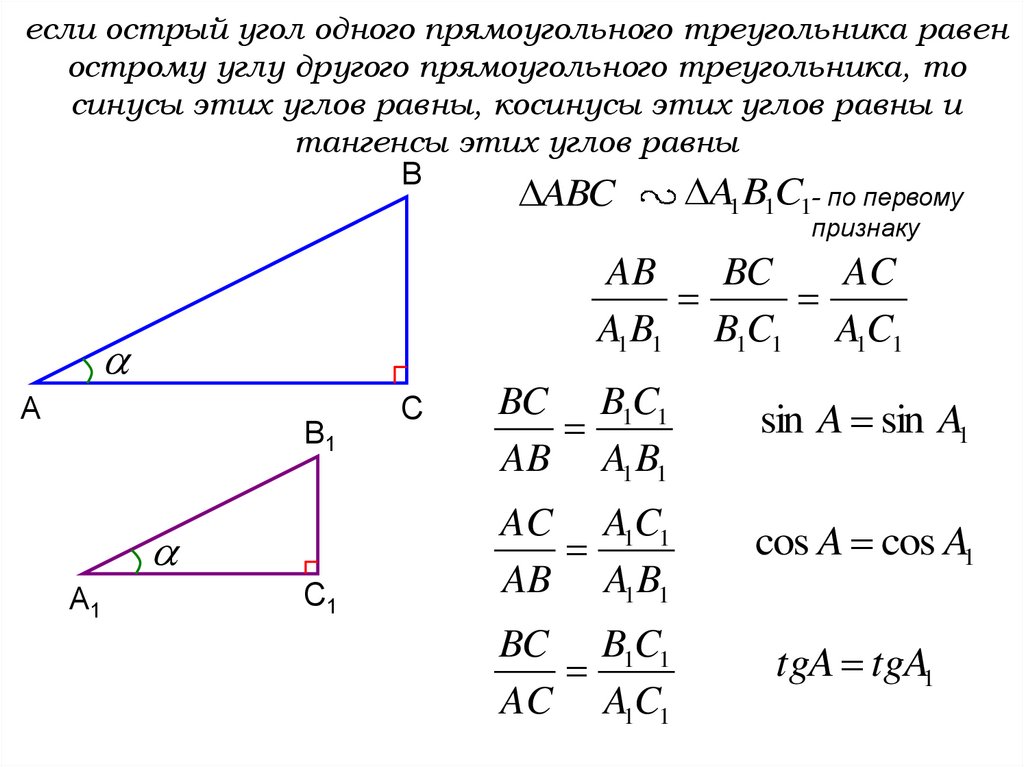
если острый угол одного прямоугольного треугольника равен
острому углу другого прямоугольного треугольника, то
синусы этих углов равны, косинусы этих углов равны и
тангенсы этих углов равны
В
ABC
признаку
AB
BC
AC
A1 B1 B1C1 A1C1
А
В1
А1
A1B1C1- по первому
С1
С
BC B1C1
AB A1 B1
sin A sin A1
AC A1C1
AB A1 B1
cos A cos A1
BC B1C1
AC A1C1
tgA tgA1

21.

22. Синусом острого угла прямоугольного треугольника называется отношение …

1)
2)
3)
Противолежащего катета к прилежащему
катету;
Противолежащего катета к гипотенузе;
Прилежащего катета к гипотенузе
противолежащий катет
sin A
гипотенуза

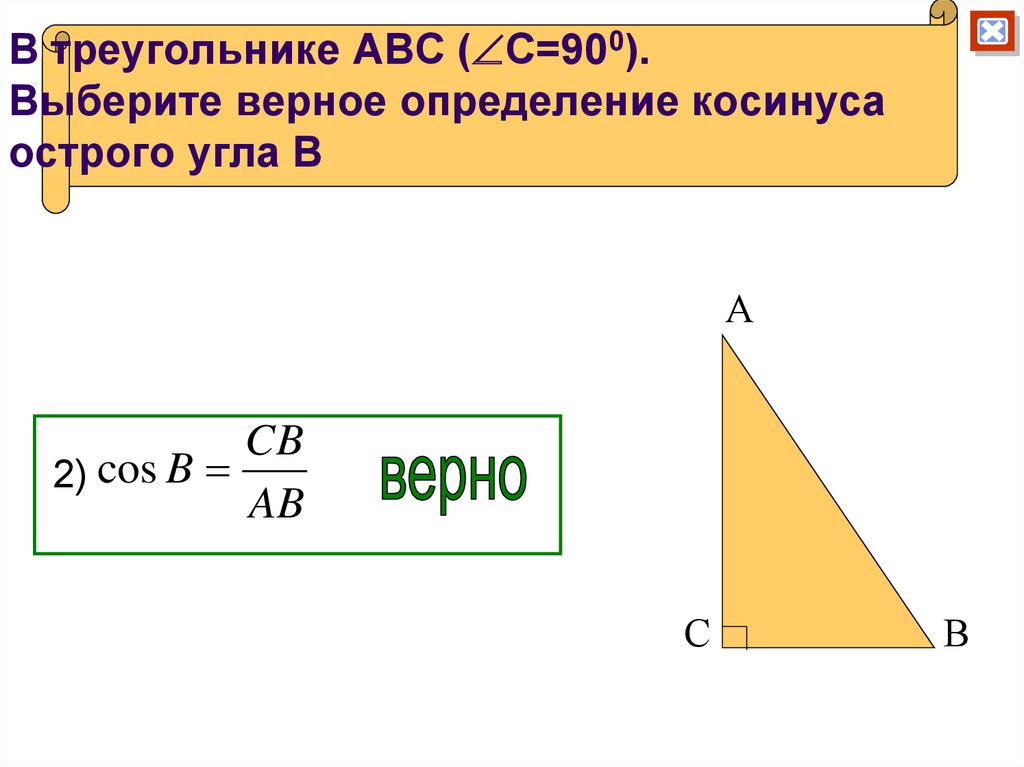
23. В треугольнике АВС (С=900). Выберите верное определение косинуса острого угла В

В треугольнике АВС ( С=900).
Выберите верное определение косинуса
острого угла В
CB
1) cos B
AC
А
CB
2) cos B
AB
AC
3) cos B
AB
С
В

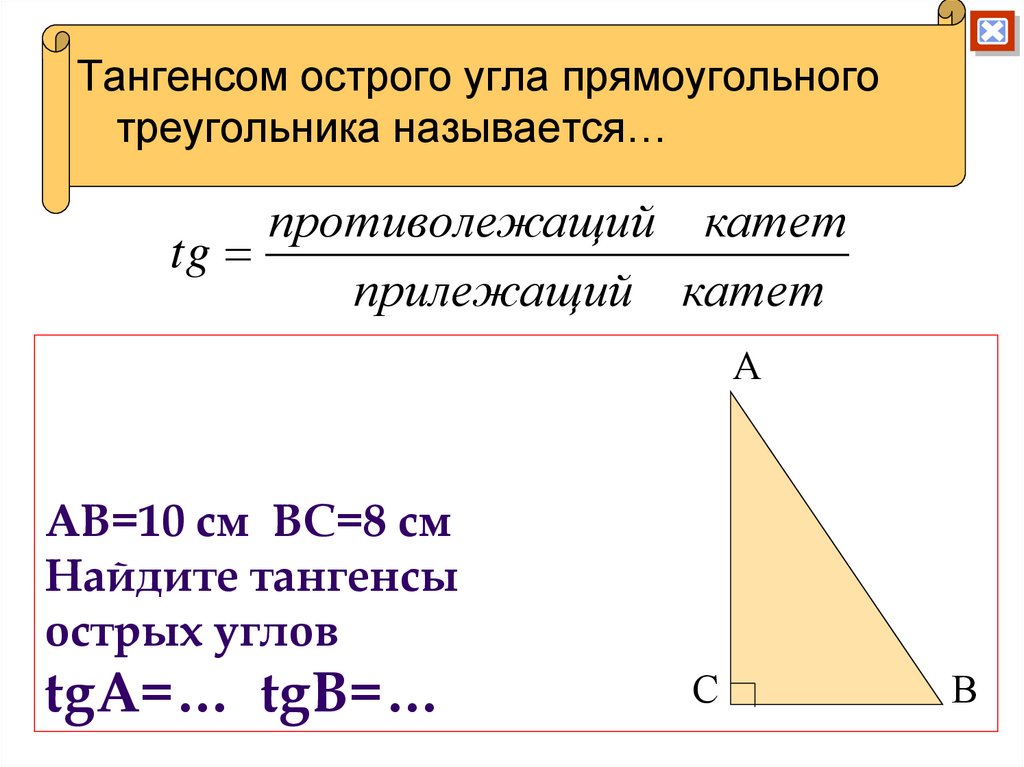
24. АВ=10 см ВС=8 см Найдите тангенсы острых углов tgA=… tgB=…

Тангенсом острого угла прямоугольного
треугольника называется…
противолежащий катет
tg
прилежащий катет
А
АВ=10 см ВС=8 см
Найдите тангенсы
острых углов
tgA=… tgB=…
С
В

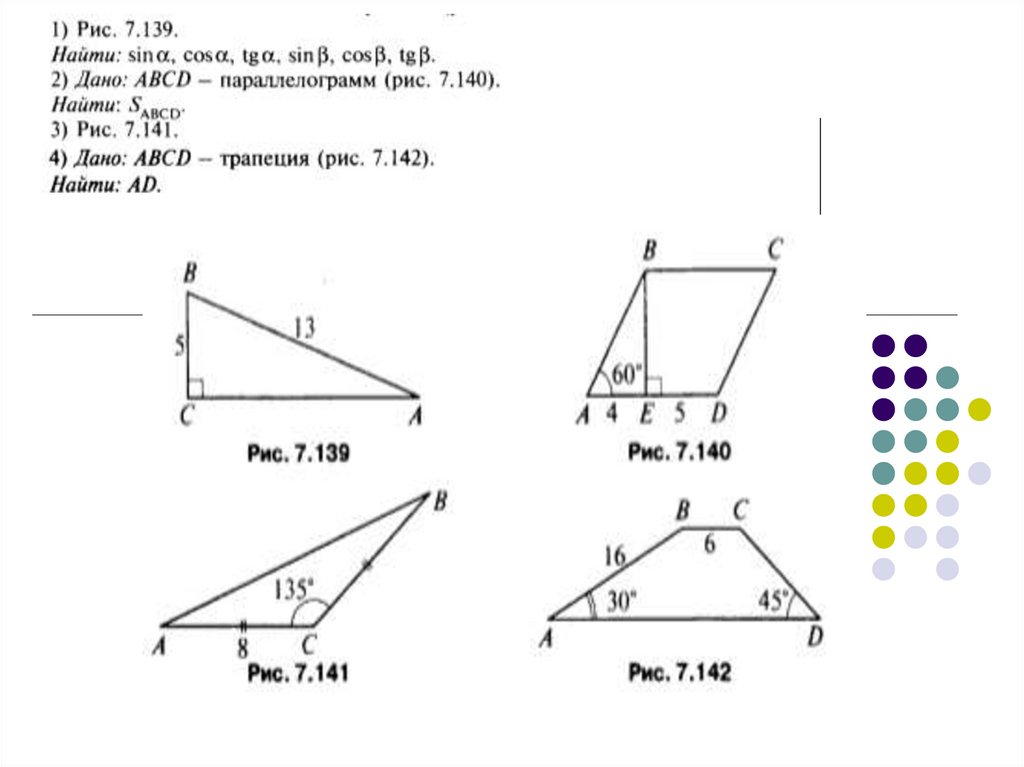
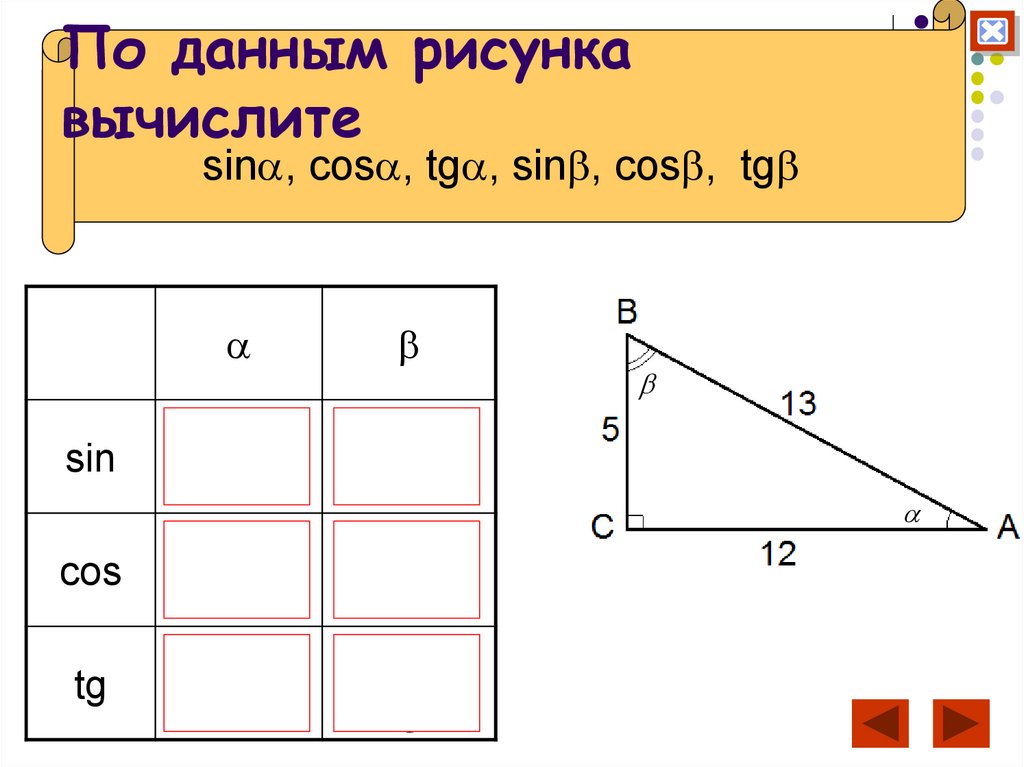
25. По данным рисунка вычислите

sin , cos , tg , sin , cos , tg
sin
cos
tg
5
13
12
13
5
12
12
13
5
13
12
5

26.

Тема урока: «Значения синуса,
косинуса и тангенса для углов 300,
450 и 600»
Цели урока:
Научится вычислять значения синуса, косинуса и
тангенса для углов 300, 450 и 600.
Формировать навыки решения прямоугольных
треугольников, используя синус, косинус и тангенс
острого угла.
Использовать различные приемы для вычисления
значений тригонометрических функций, в том числе и
компьютерные программы.

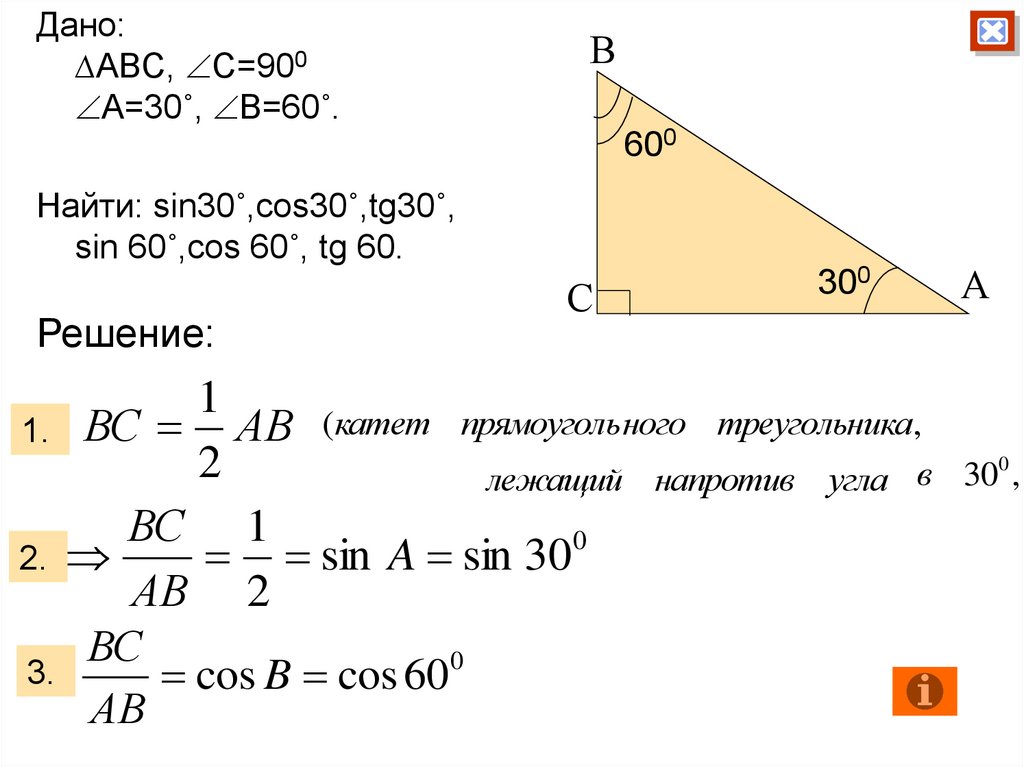
27.

Дано:
∆ABC, C=900
A=30˚, B=60˚.
В
600
Найти: sin30˚,cos30˚,tg30˚,
sin 60˚,cos 60˚, tg 60.
Решение:
С
300
1
АВ (катет прямоугольного треугольника,
1. ВС
2
лежащий напротив угла в
ВС 1
0
2.
sin A sin 30
АВ 2
ВС
3.
cos B cos 60 0
АВ
А
300 ,

28.

В
1
sin 30 cos 60
2
0
0
600
Вычислим sin600 и cos300
Основное
С
тригонометрическое тождество:
300
А
sin2 +cos2 =1 sin2 =1-cos2 sin 1 cos 2
1
3
sin 60 1 cos 60 1
4
2
0
2
0
cos2 =1-sin2 cos 1 sin 2
3
cos 30 1 sin 30
2
0
2
0

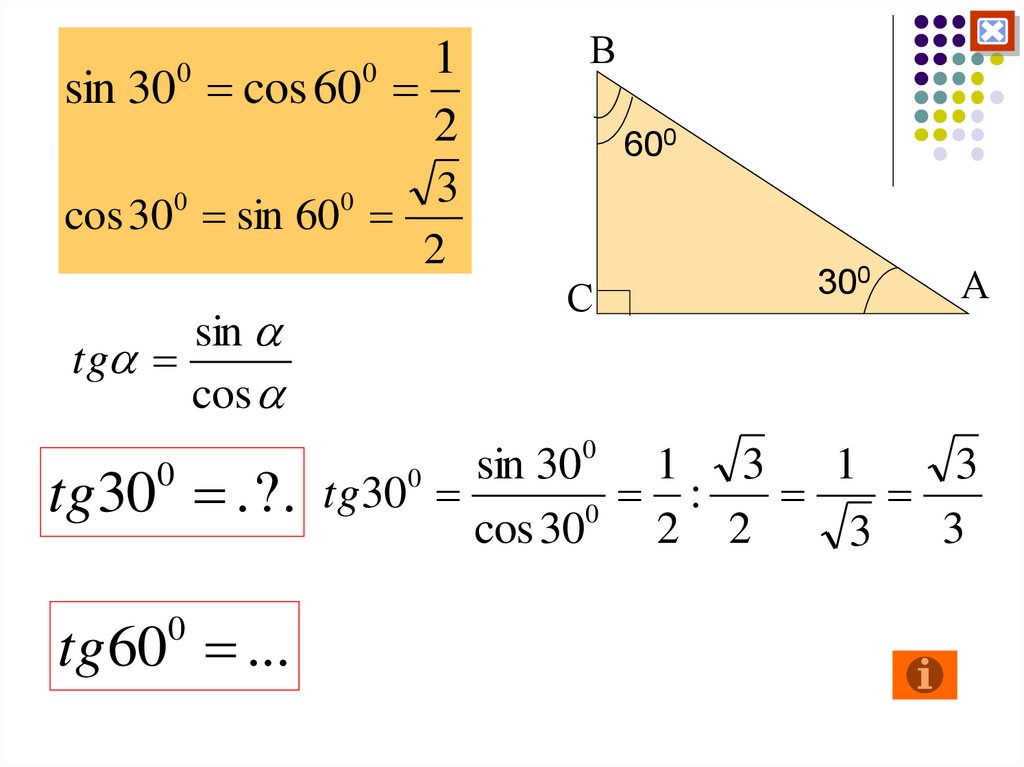
29.

1
sin 30 cos 60
2
0
0
В
600
3
cos 30 sin 60
2
0
0
С
sin
tg
cos
tg30 . ? .
0
tg 60 ...
0
0
300
А
sin 30
1 3
1
3
tg30
:
0
cos 30
2 2
3
3
0

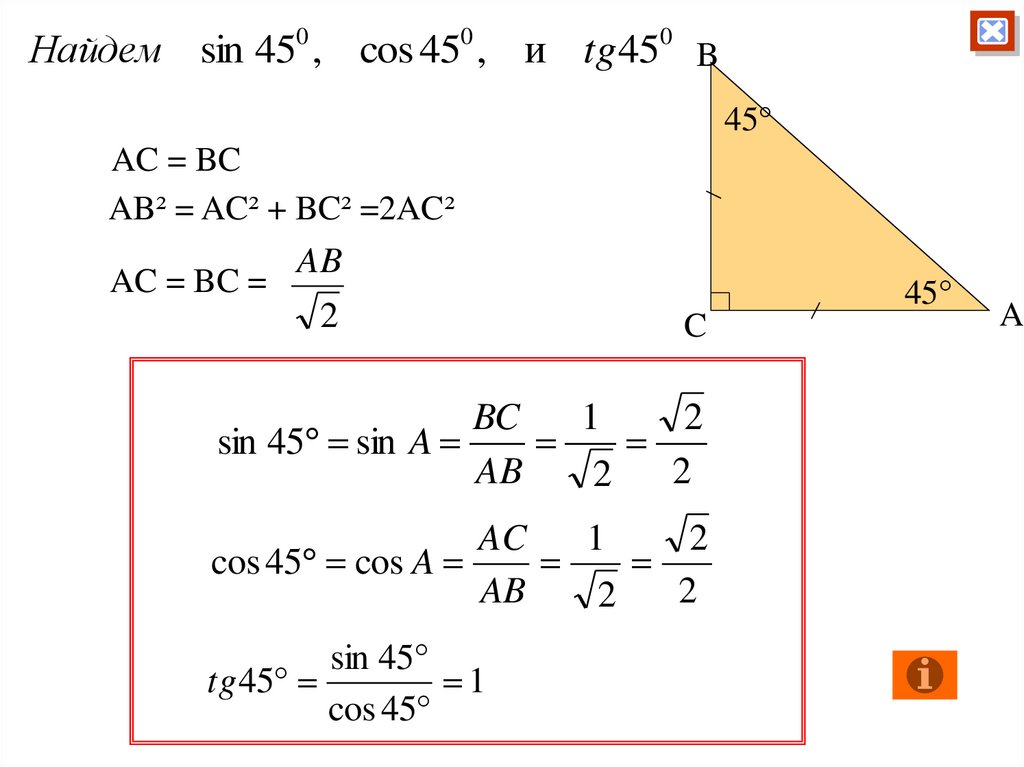
30.

Найдем sin 450 , cos 450 , и tg 450 B
45°
AC = BC
AB² = AC² + BC² =2AC²
AC = BC =
AB
2
45°
C
BC
1
2
sin 45 sin A
AB
2
2
AC
1
2
cos 45 cos A
AB
2
2
sin 45
tg 45
1
cos 45
A

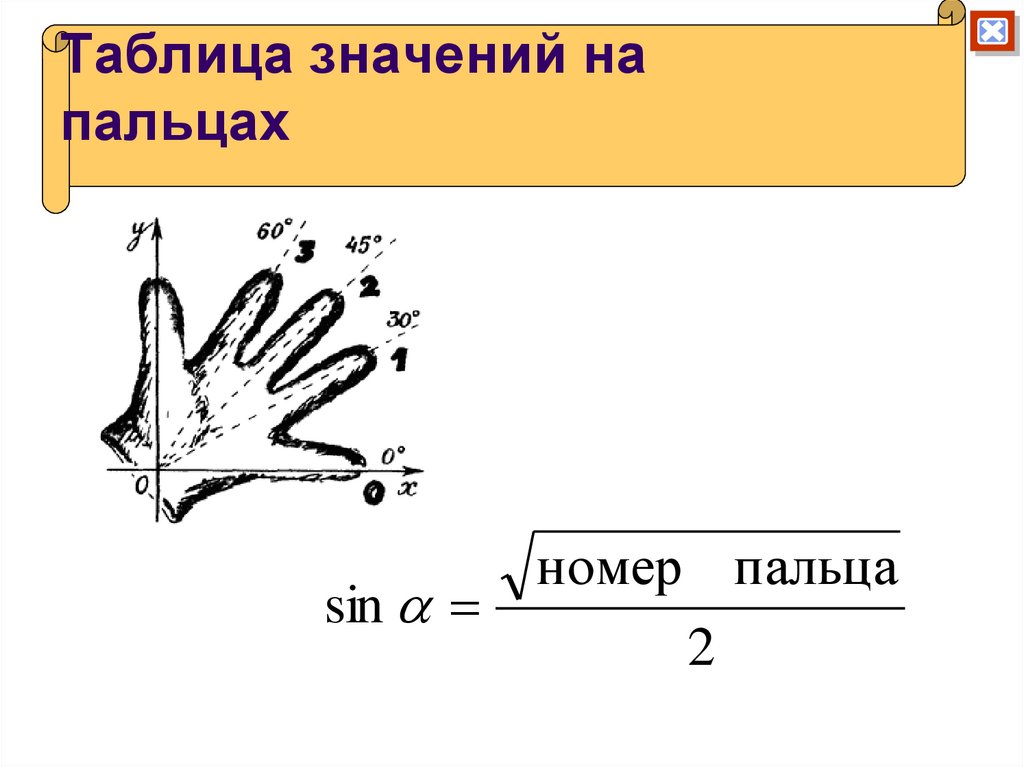
31. Таблица значений на пальцах

sin
номер пальца
2

32.

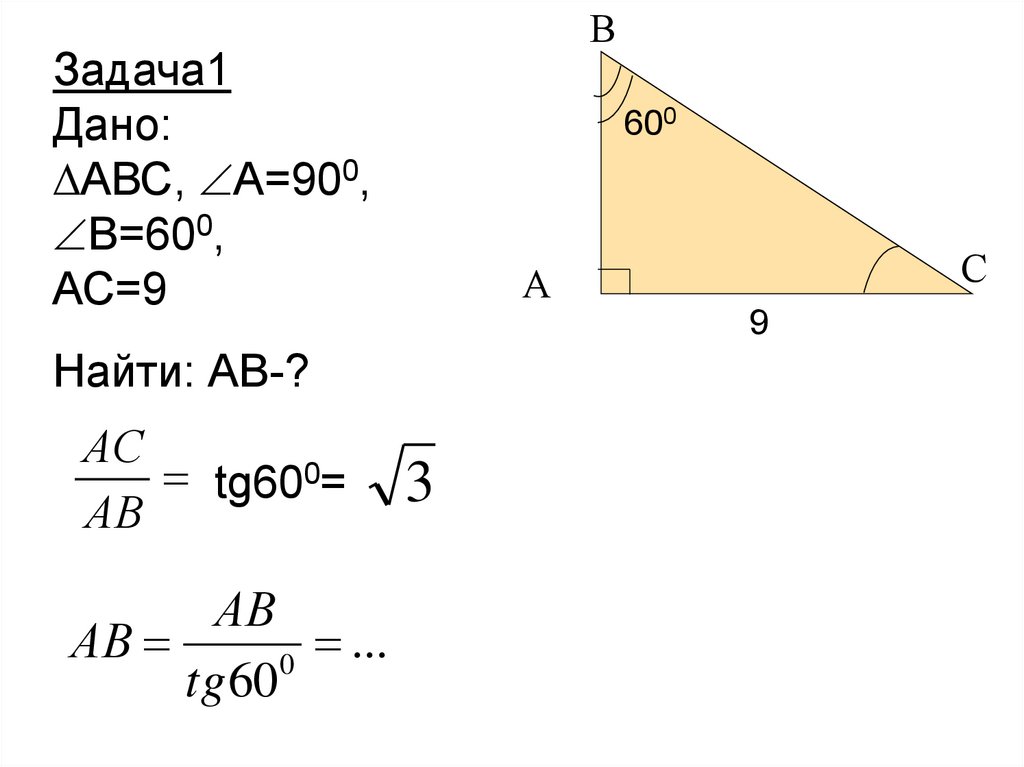
В
Задача1
Дано:
∆АВС, А=900,
В=600,
АС=9
600
9
Найти: АВ-?
АС
tg600=
АВ
АВ
АВ
...
0
tg 60
С
А
3

33.

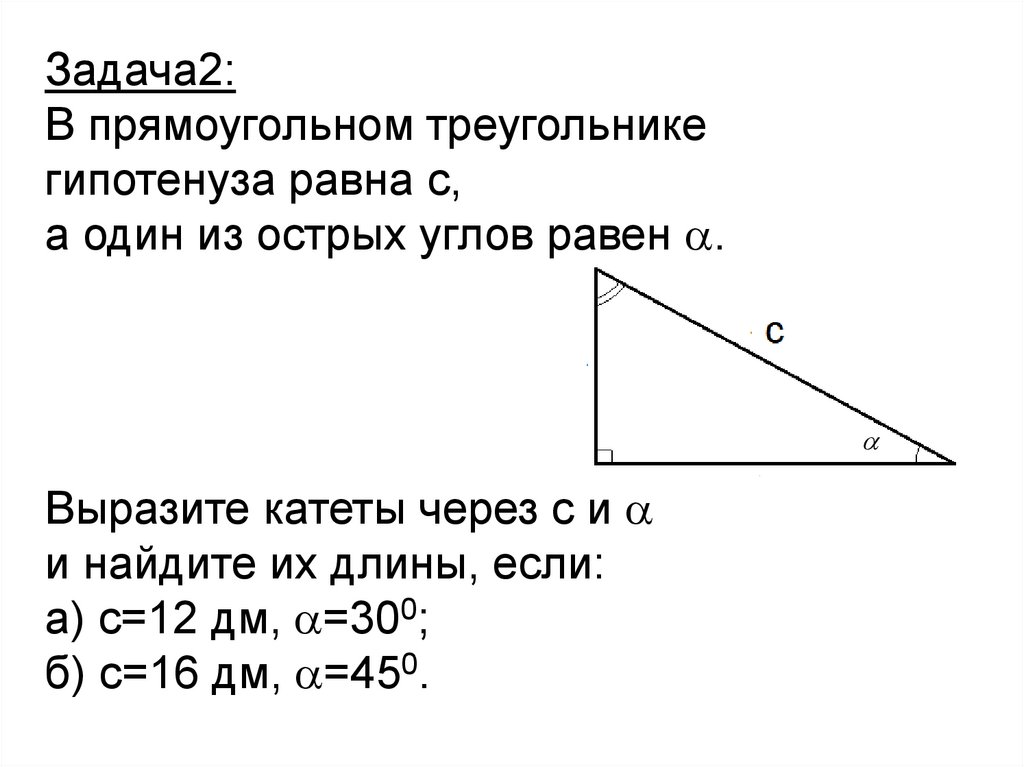
Задача2:
В прямоугольном треугольнике
гипотенуза равна с,
а один из острых углов равен .
Выразите катеты через с и
и найдите их длины, если:
а) с=12 дм, =300;
б) с=16 дм, =450.

34.

300
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tg
3
3
1
450
600
3

35.

300
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tg
3
3
1
450
600
3

36.

37.

c
а
a = c sin
b = c cos
b
a = b tg
b = a ctg

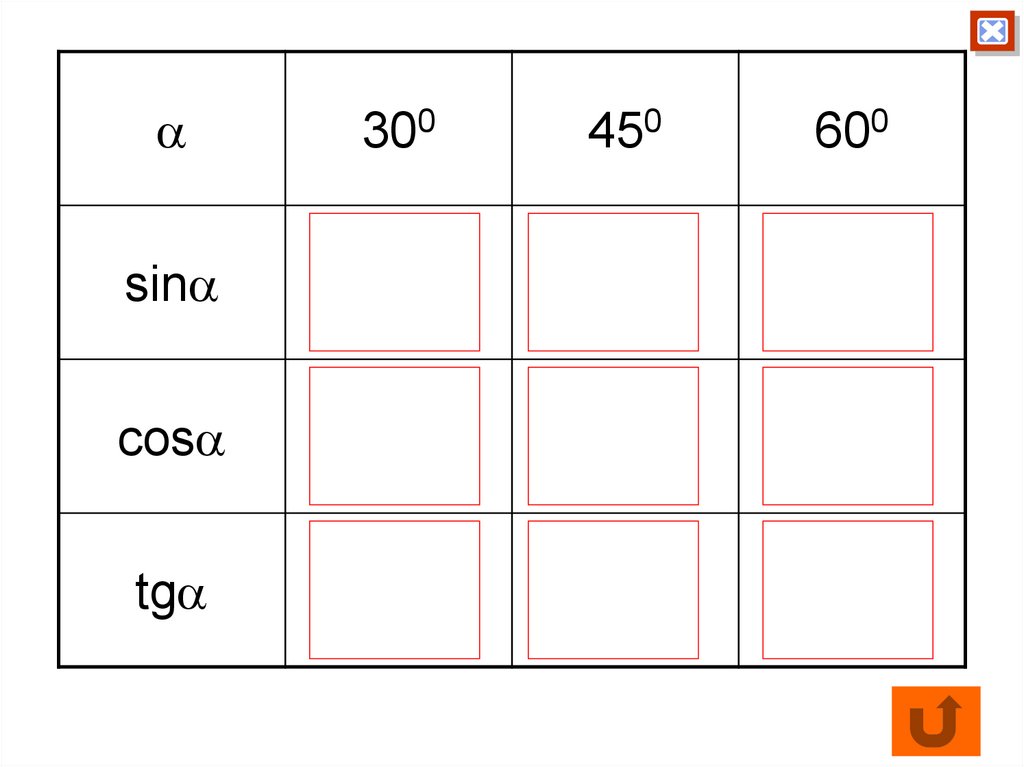
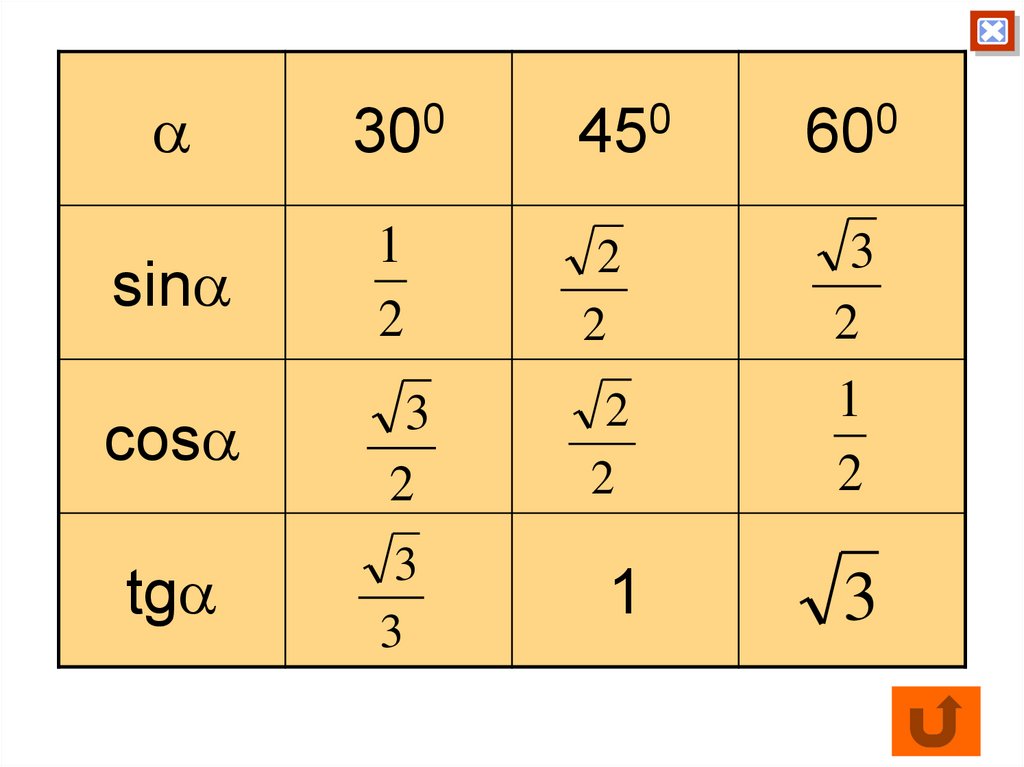
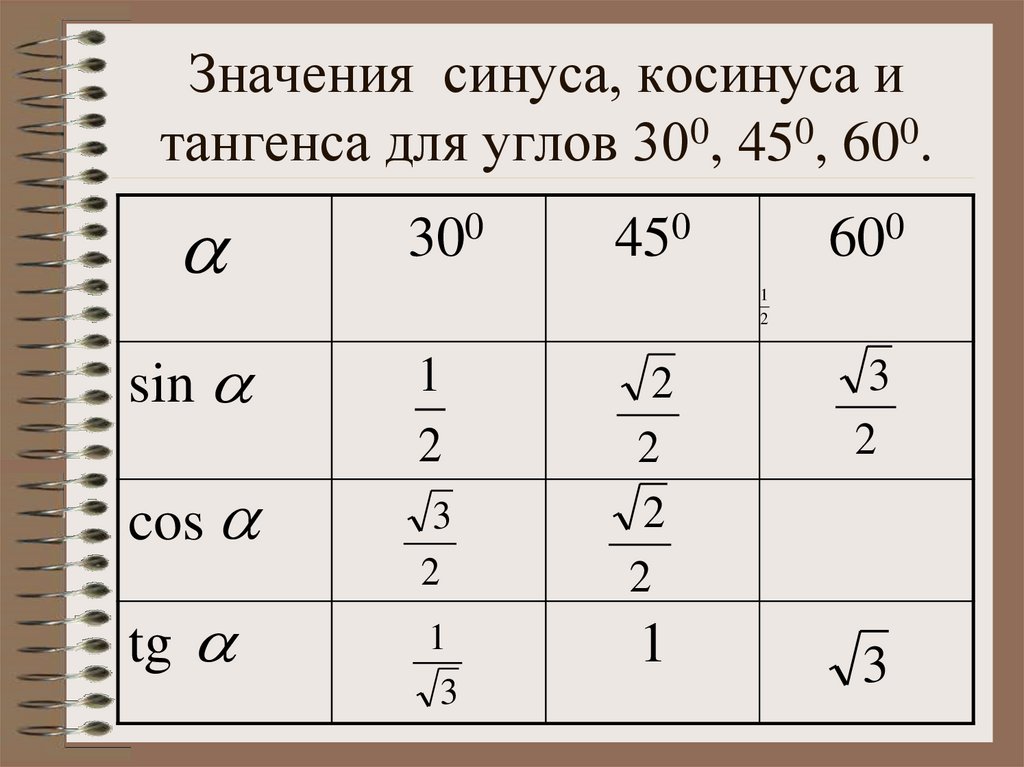
38. Значения синуса, косинуса и тангенса для углов 300, 450, 600.

sin
cos
tg
300
450
600
1
2
1
2
3
2
1
3
2
2
2
2
1
3
2
3

39. З а д а ч а

Задача
В прямоугольном треугольнике
даны гипотенуза с и острый
угол α. Найти катеты, их
проекции на гипотенузу и
высоту, опущенную на
гипотенузу.

40. Решение

C
α
A
D
c
B
AC = AB cos α = c cos α;
BC = AB sin α = c sin α;
BD = BC sin α = c sin² α;
AD = AC cos α = c cos² α;
СВ = AC sin α = c sin α cos α

41.

III. Закрепление изученного
материала
Решение прикладных
задач

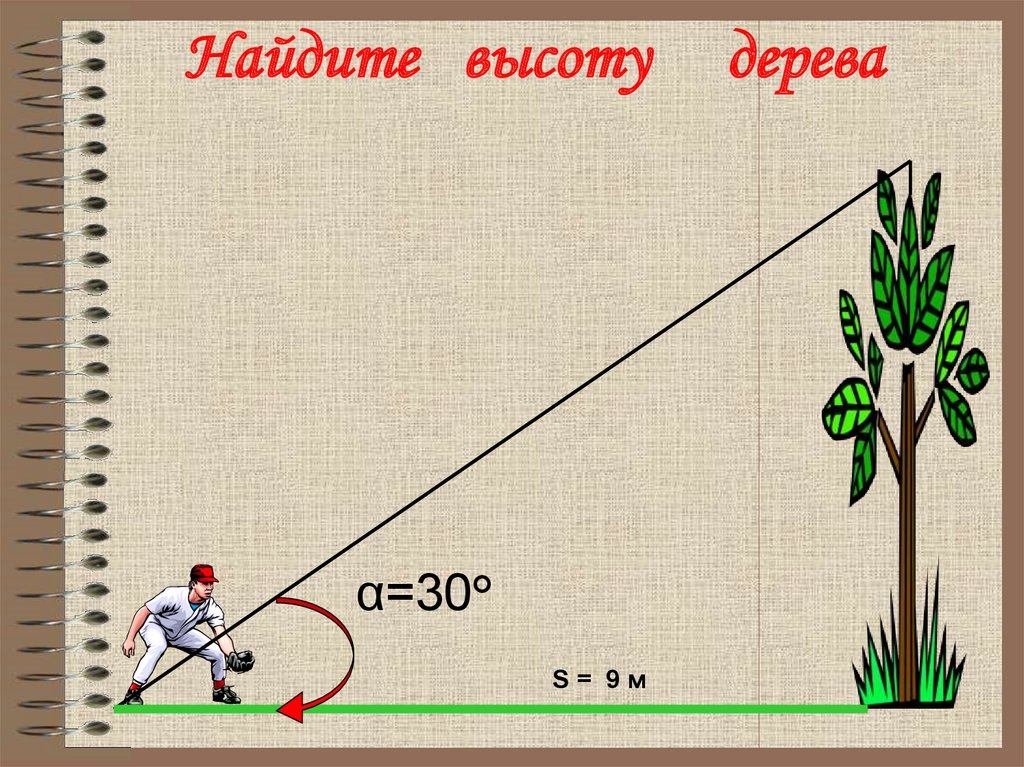
42. Найдите высоту дерева

Найдите высоту
α=30°
S= 9м
дерева

43. Найдите угол наклона Пизанской башни

h 1 = 60 м
21
h 2 = 50 м
α=?

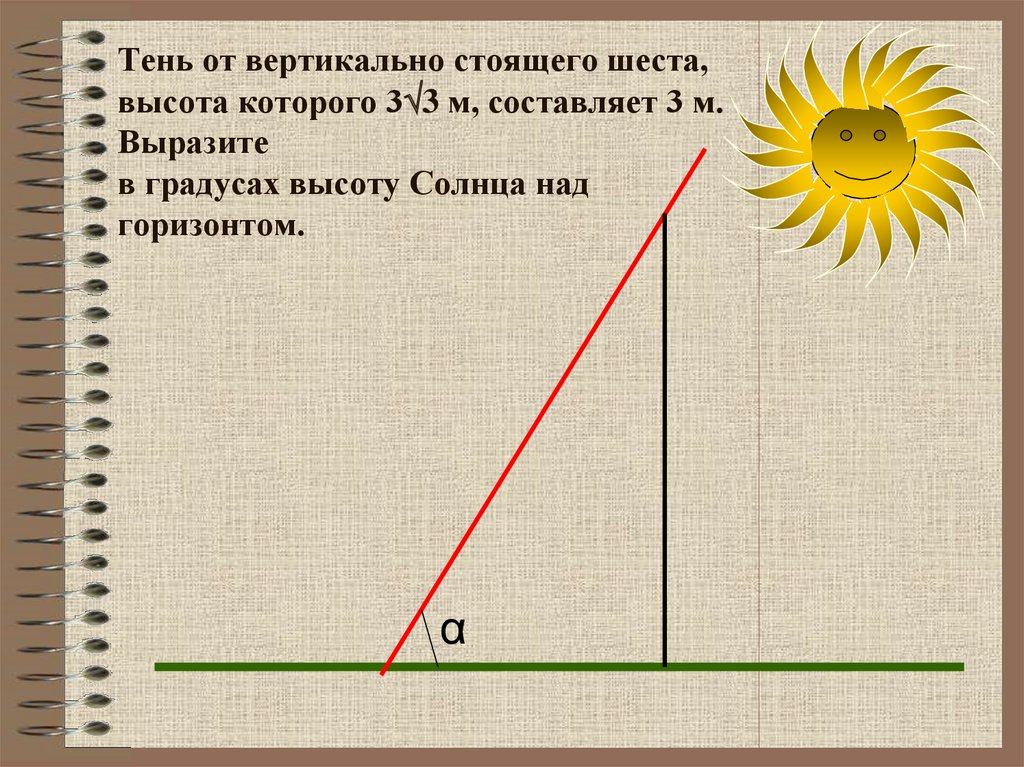
44. Тень от вертикально стоящего шеста, высота которого 33 м, составляет 3 м. Выразите в градусах высоту Солнца над горизонтом.

Тень от вертикально стоящего шеста,
высота которого 3 3 м, составляет 3 м.
Выразите
в градусах высоту Солнца над
горизонтом.
α