Similar presentations:
Соотношения между сторонами и углами прямоугольного треугольника
1. Соотношения между сторонами и углами прямоугольного треугольника
АВ
С
2. Акутализация знаний:
• Какой треугольник называетсяпрямоугольным?
• Чему равна сумма острых углов
прямоугольного треугольника?
• Как называются стороны
прямоугольного треугольника?
• Повторим теорему Пифагора
• Чему равен катет прямоугольного
треугольника, лежащий против угла в
30º?
3.
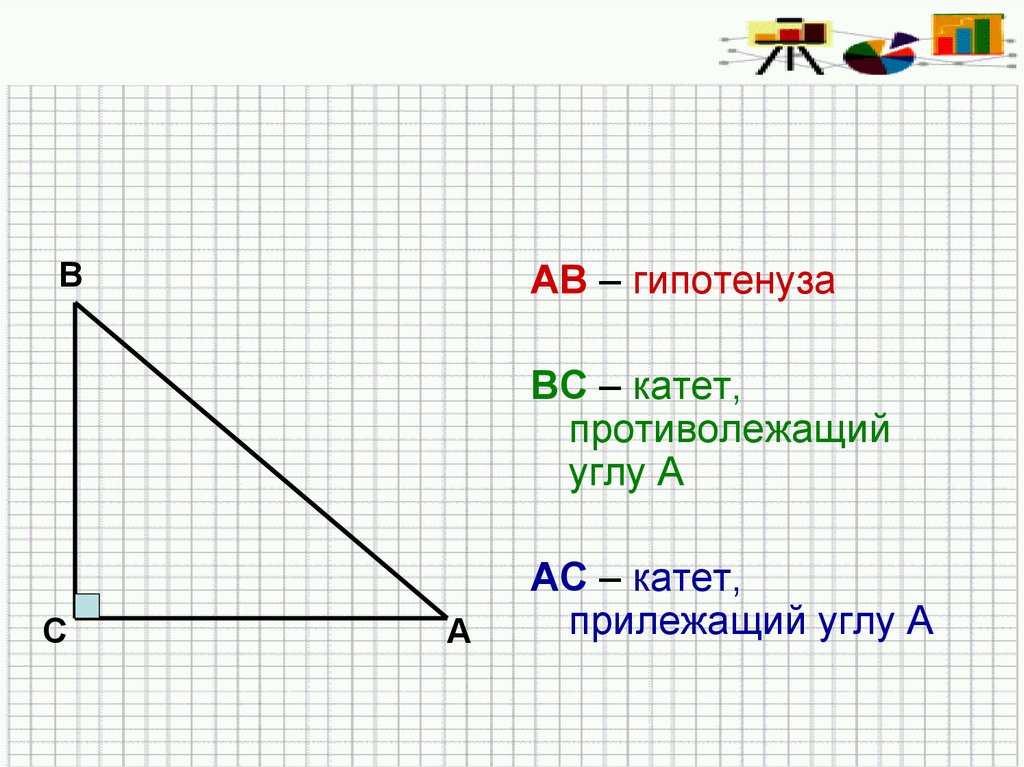
ВАВ – гипотенуза
ВС – катет,
противолежащий
углу А
С
А
АС – катет,
прилежащий углу А
4.
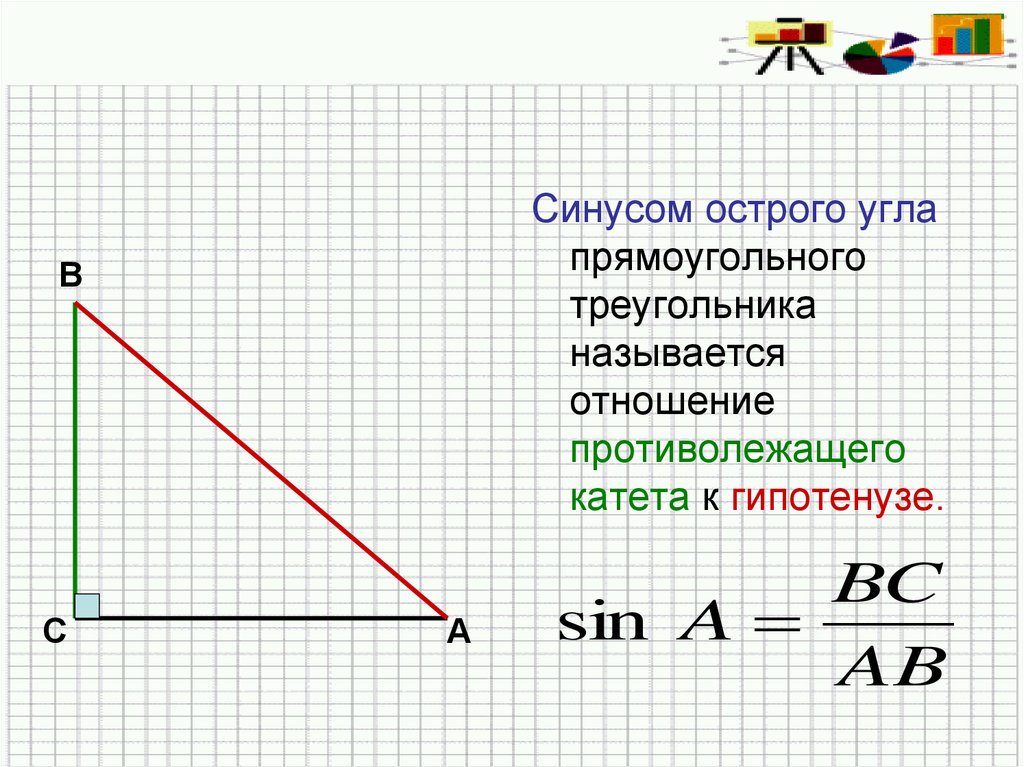
Синусом острого углапрямоугольного
треугольника
называется
отношение
противолежащего
катета к гипотенузе.
В
С
А
BC
sin A
AB
5.
Косинусом острогоугла прямоугольного
треугольника
называется
отношение
прилежащего катета
к гипотенузе.
В
С
А
AC
cos A
AB
6.
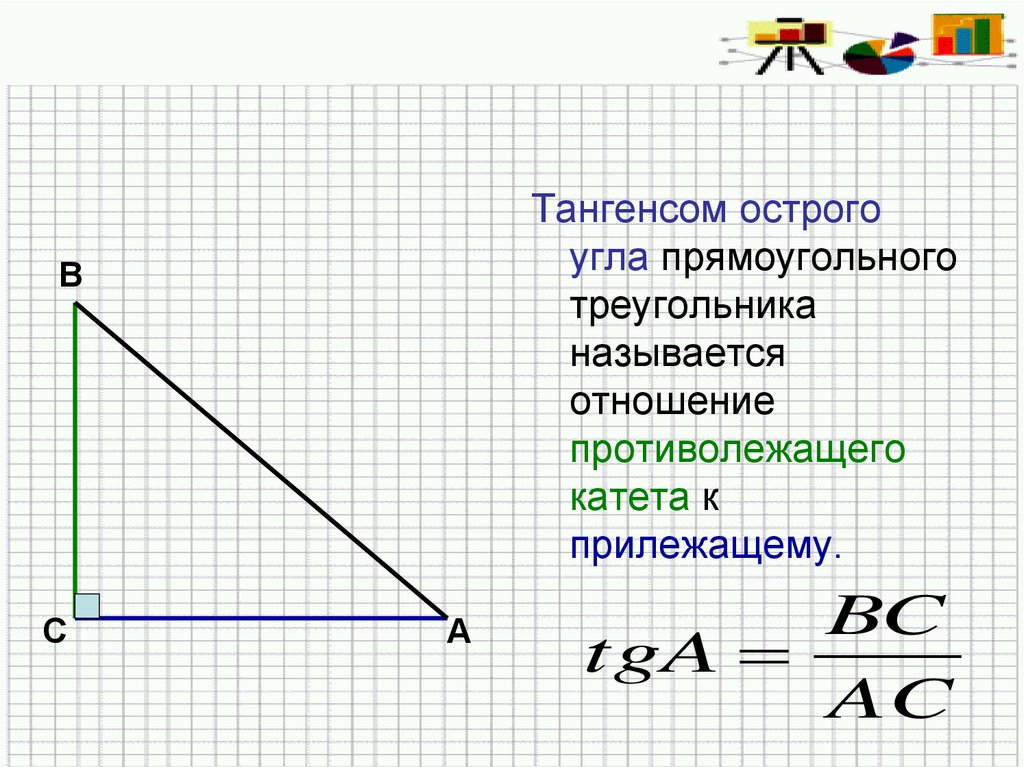
Тангенсом острогоугла прямоугольного
треугольника
называется
отношение
противолежащего
катета к
прилежащему.
В
С
А
BC
tgA
AC
7. Тригонометрические тождества
1)Основное тригонометрическое тождество:
sin A cos A 1
2
2
2) Тангенс угла равен отношению синуса к
косинусу этого угла.
sin A
tgA
cos A
П
8. Таблица значений для углов, равных 300, 450, 600.
Таблица значенийsin , cos , tg
для углов, равных 300, 450, 600.
sin
cos
tg
300
450
600
9. Значения синуса, косинуса и тангенса угла 30° .
Рассмотрим прямоугольныйтреугольник АВС:
А=30°, В=60°
Так как катет, лежащий против
угла 30°, равен половине
гипотенузы, то BC 1
AB
2
BC
1
sin A
AB
2
1
o
Значит, sin 30 .
2
Но
В
60°
Из основного тригонометрического
тождества получаем
cos 30o 1 sin 2 30o 1
С
30°
А
1
3
4
2
По 2-му тождеству находим
sin 30o 1 3 1 2
1
3
tg30
:
cos 30o 2 2 2 3
3 3
o
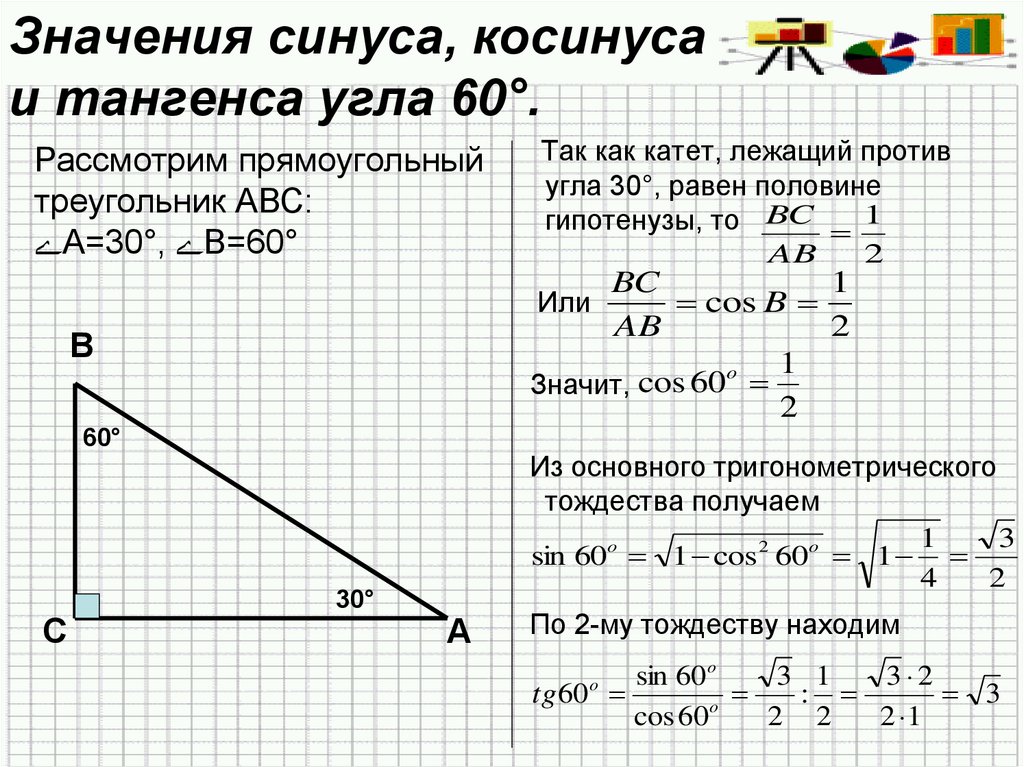
10. Значения синуса, косинуса и тангенса угла 60°.
Рассмотрим прямоугольныйтреугольник АВС:
А=30°, В=60°
Так как катет, лежащий против
угла 30°, равен половине
гипотенузы, то BC 1
AB
2
BC
1
cos B
AB
2
1
o
Значит, cos 60
2
Или
В
60°
С
30°
Из основного тригонометрического
тождества получаем
1
3
sin 60o 1 cos 2 60o 1
4
2
А
По 2-му тождеству находим
sin 60o
3 1
3 2
tg 60
:
3
o
cos 60
2 2
2 1
o
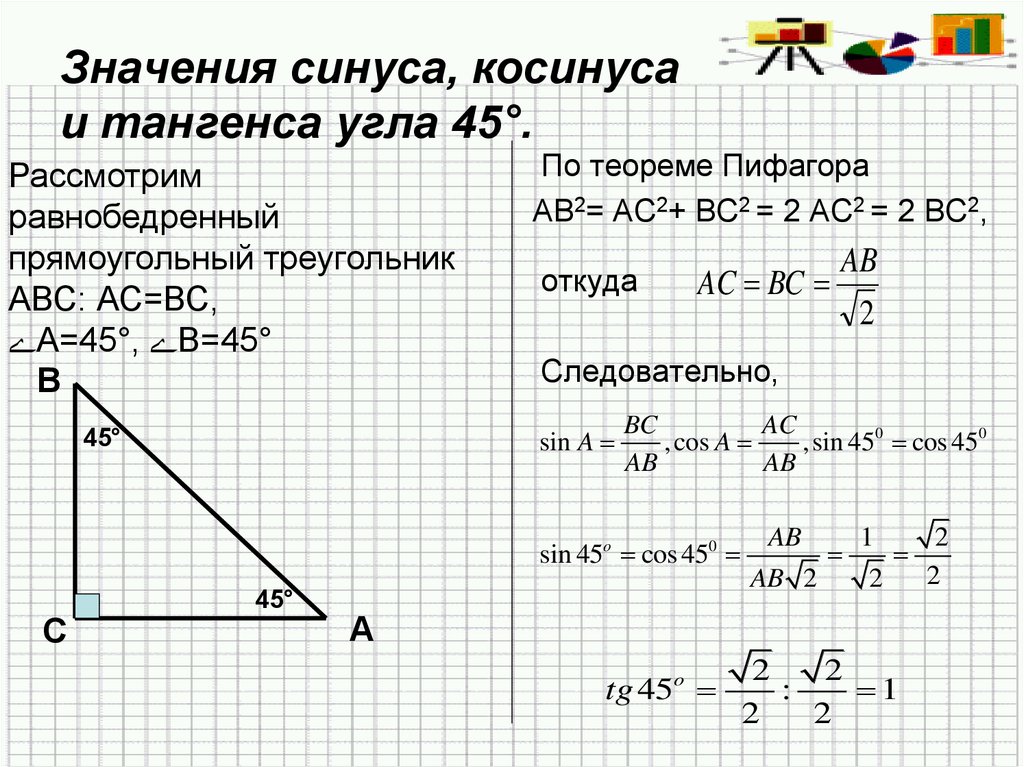
11. Значения синуса, косинуса и тангенса угла 45°.
Рассмотримравнобедренный
прямоугольный треугольник
АВС: АС=ВС,
А=45°, В=45°
В
По теореме Пифагора
АВ2= АС2+ ВС2 = 2 АС2 = 2 ВС2,
откуда
Следовательно,
sin A
45°
AB
AC BC
2
BC
AC
, cos A
,sin 450 cos 450
AB
AB
sin 45o cos 450
С
45°
AB
1
2
2
AB 2
2
А
tg 45o
2
2
:
1
2
2
12. Домашнее задание:
• 1)Учить правила, определения§4 п.66 - 67
• 2) №591







 mathematics
mathematics








