Соотношения между сторонами и углами прямоугольного треугольника

1. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

2.

3. Расположение углов и сторон

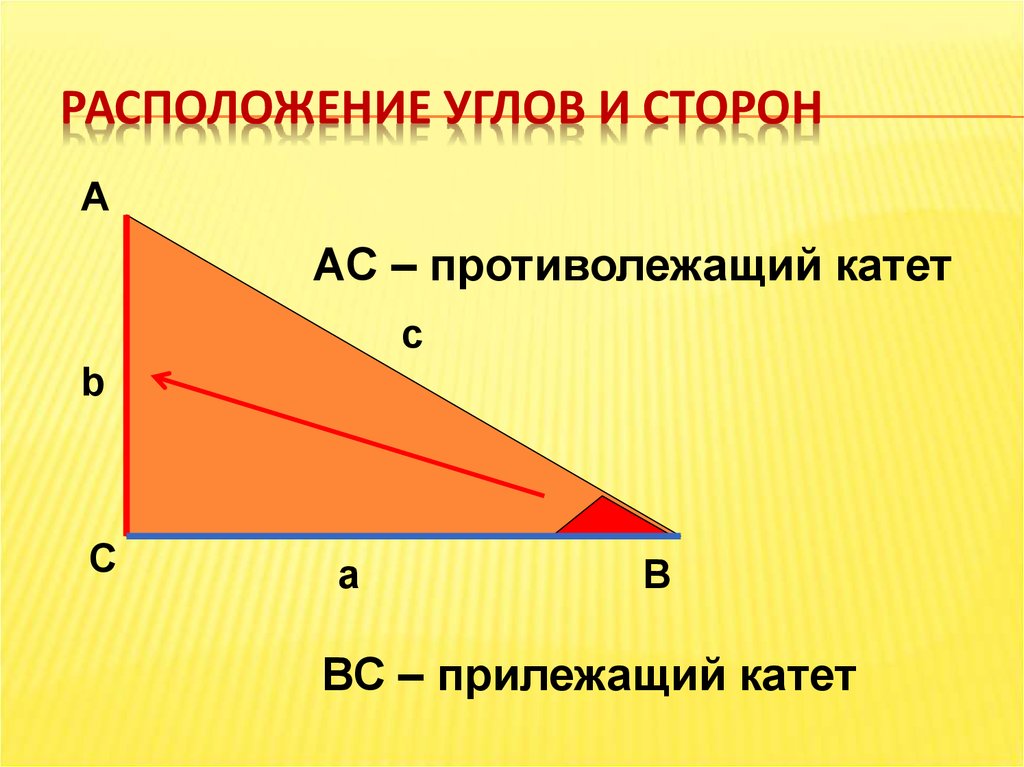
РАСПОЛОЖЕНИЕ УГЛОВ И СТОРОН
А
АС – противолежащий катет
c
b
С
a
В
ВС – прилежащий катет

4. Расположение углов и сторон

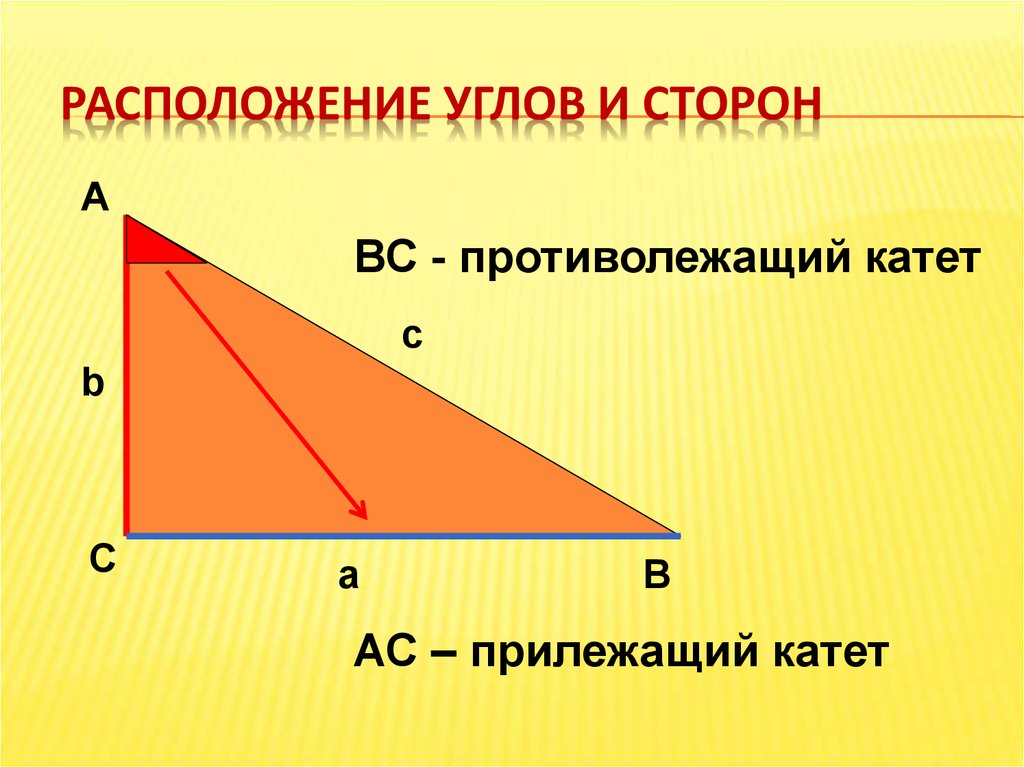
РАСПОЛОЖЕНИЕ УГЛОВ И СТОРОН
А
ВС - противолежащий катет
c
b
С
a
В
АС – прилежащий катет

5.

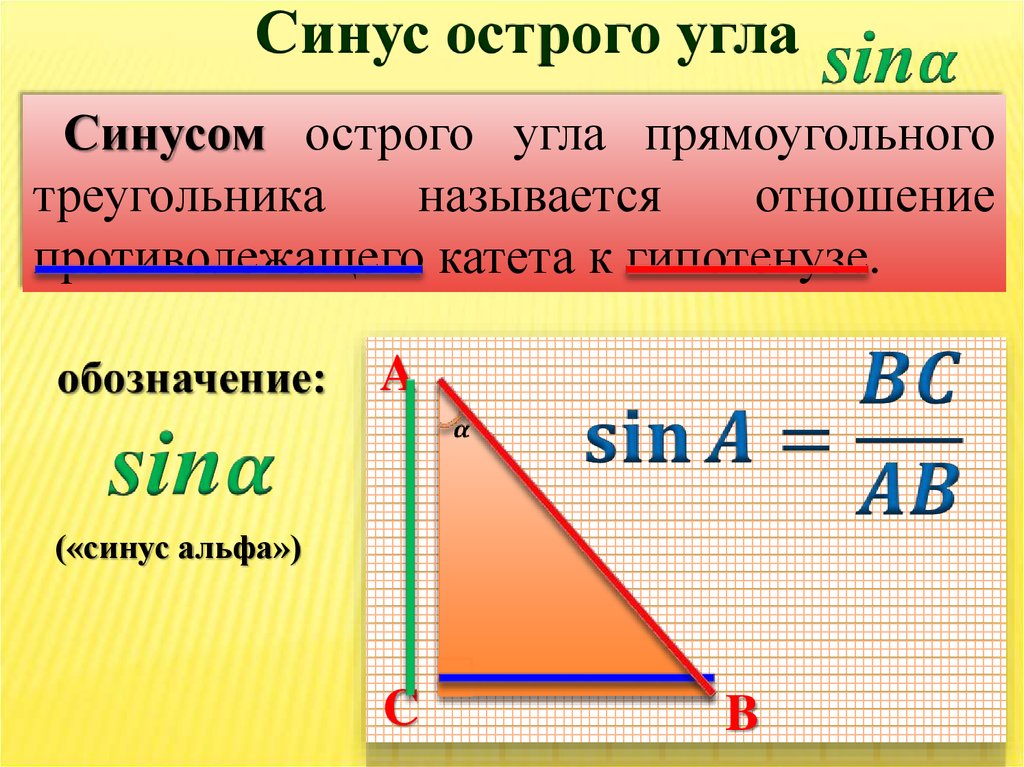
Синус острого угла
Синусом острого угла прямоугольного
треугольника
называется
отношение
противолежащего катета к гипотенузе.
A
(«синус альфа»)
C
B

6.

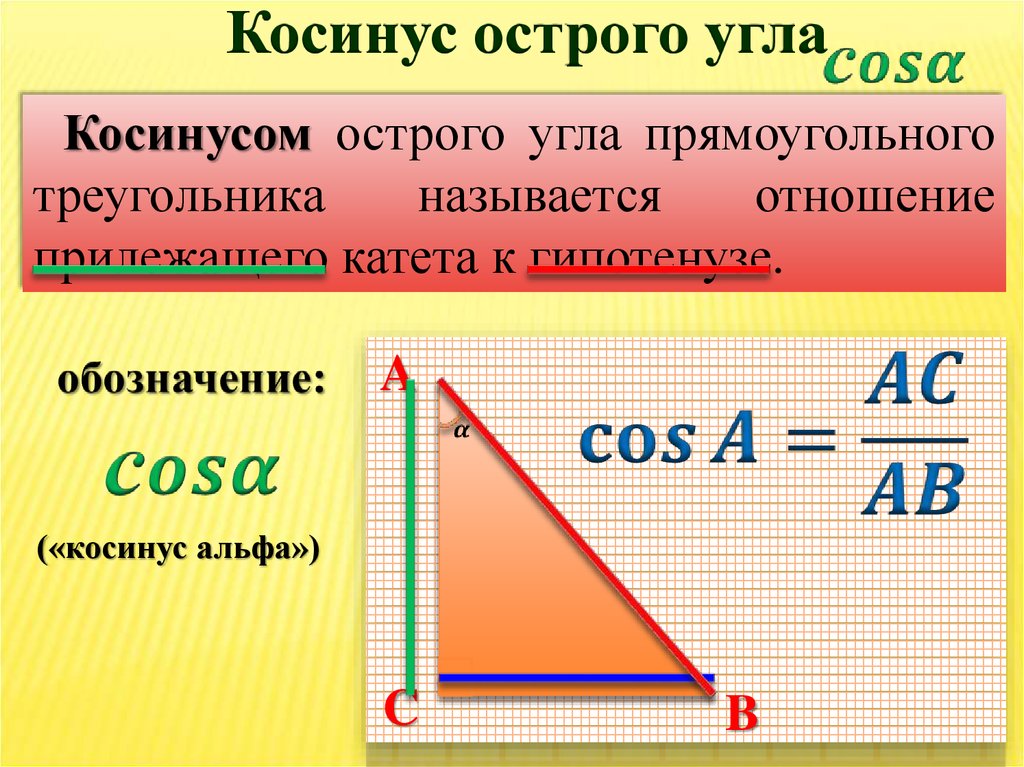
Косинус острого угла
Косинусом острого угла прямоугольного
треугольника
называется
отношение
прилежащего катета к гипотенузе.
A
(«косинус альфа»)
C
B

7.

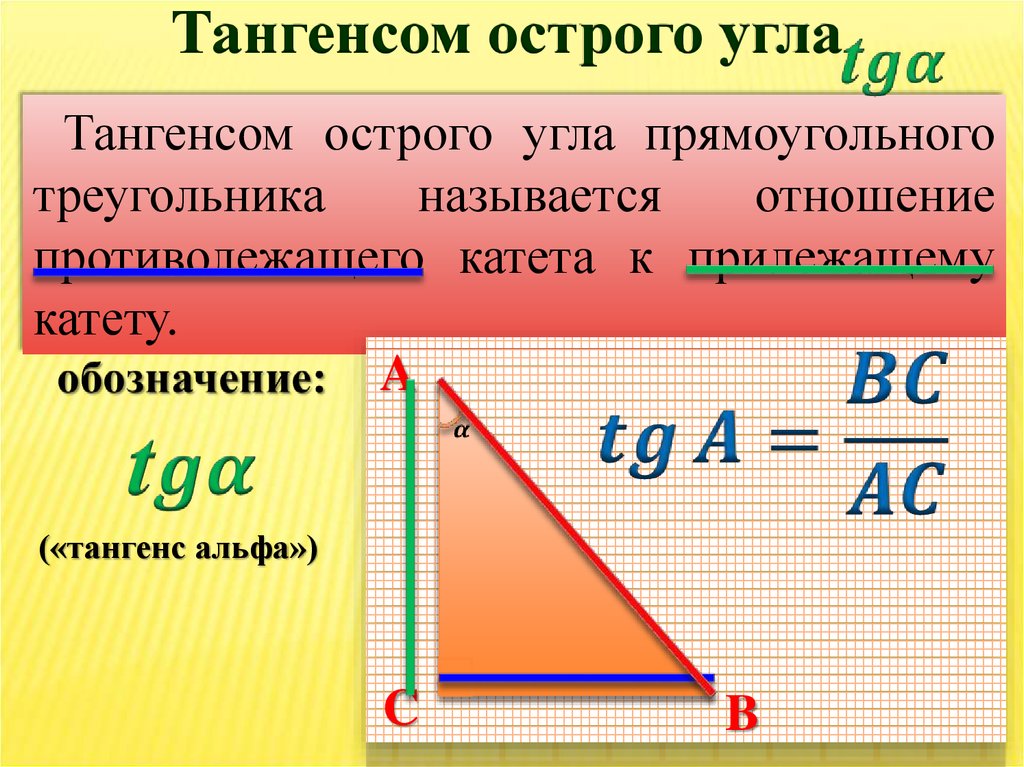
Тангенсом острого угла
Тангенсом острого угла прямоугольного
треугольника
называется
отношение
противолежащего катета к прилежащему
катету.
A
(«тангенс альфа»)
C
B

8.

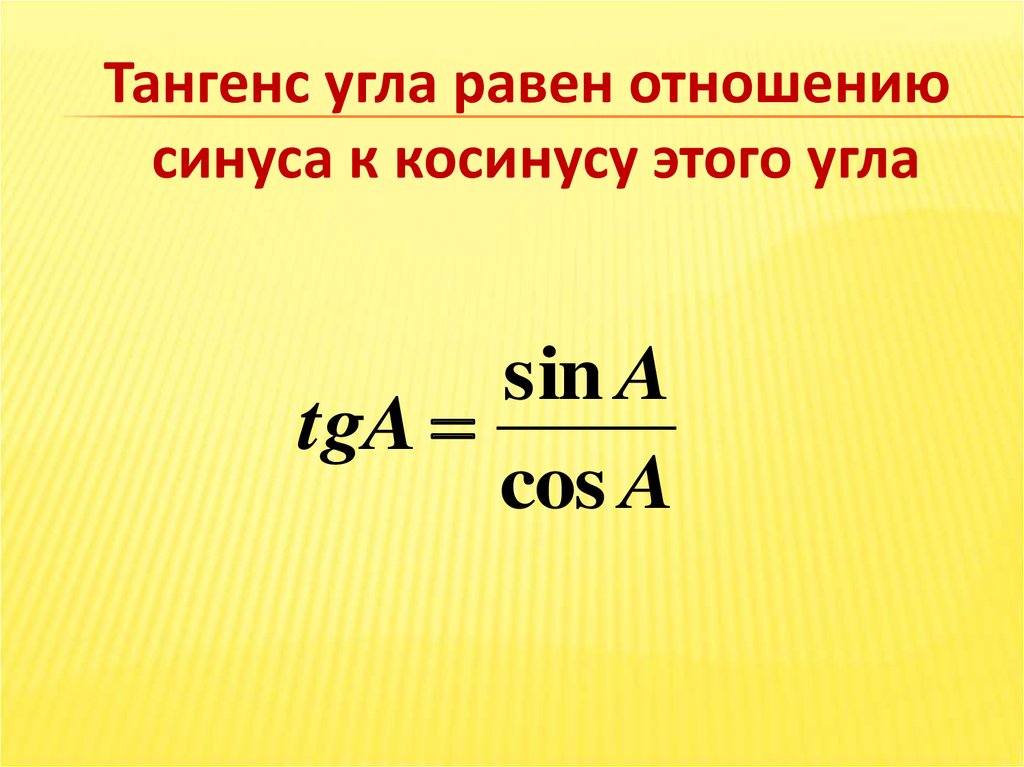
Тангенс угла равен отношению
синуса к косинусу этого угла
sin A
tgA
cos A

9.

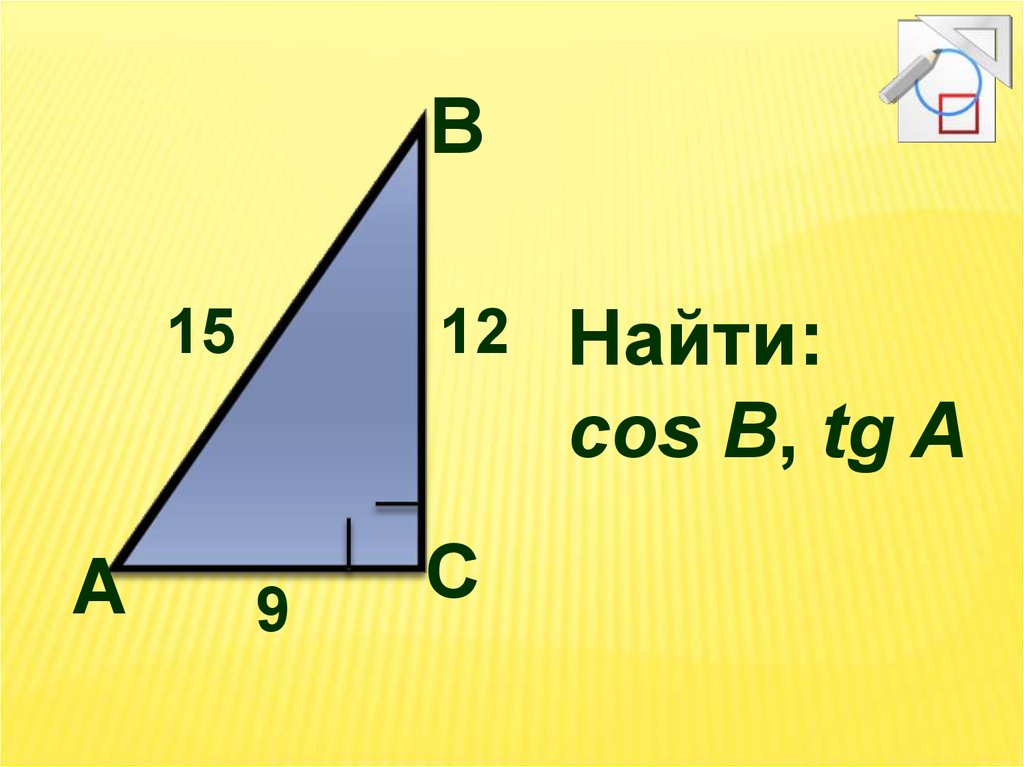
В
15
А
12
9
С
Найти:
cos B, tg A

10.

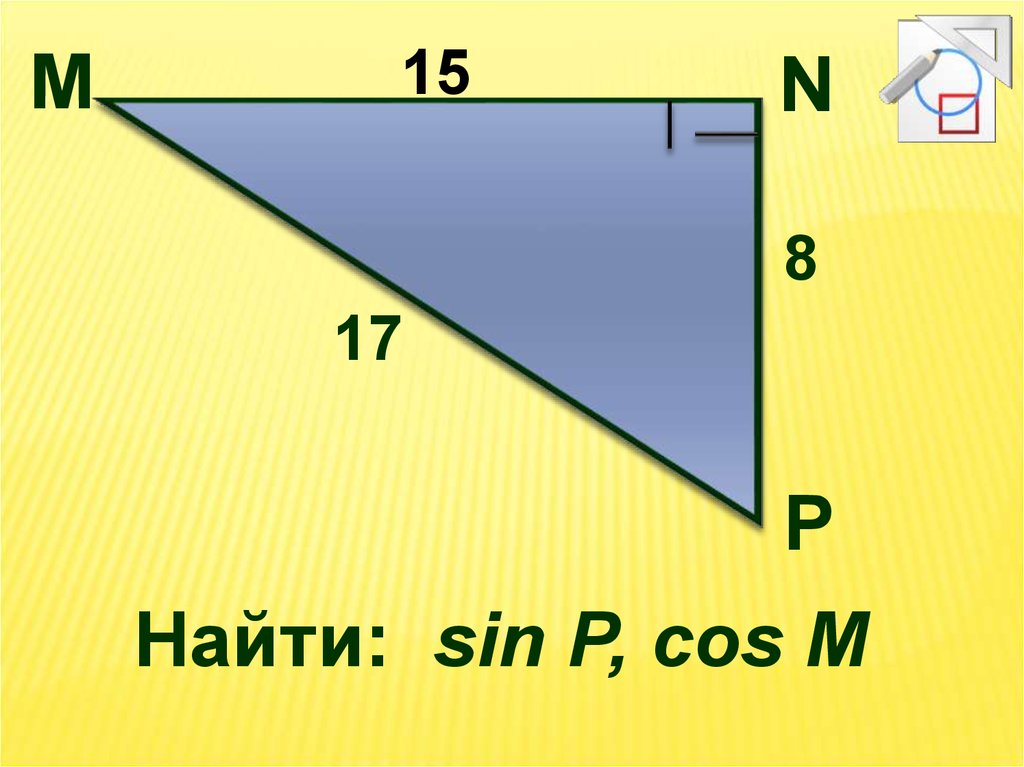
M
15
N
8
17
P
Найти: sin P, cos M

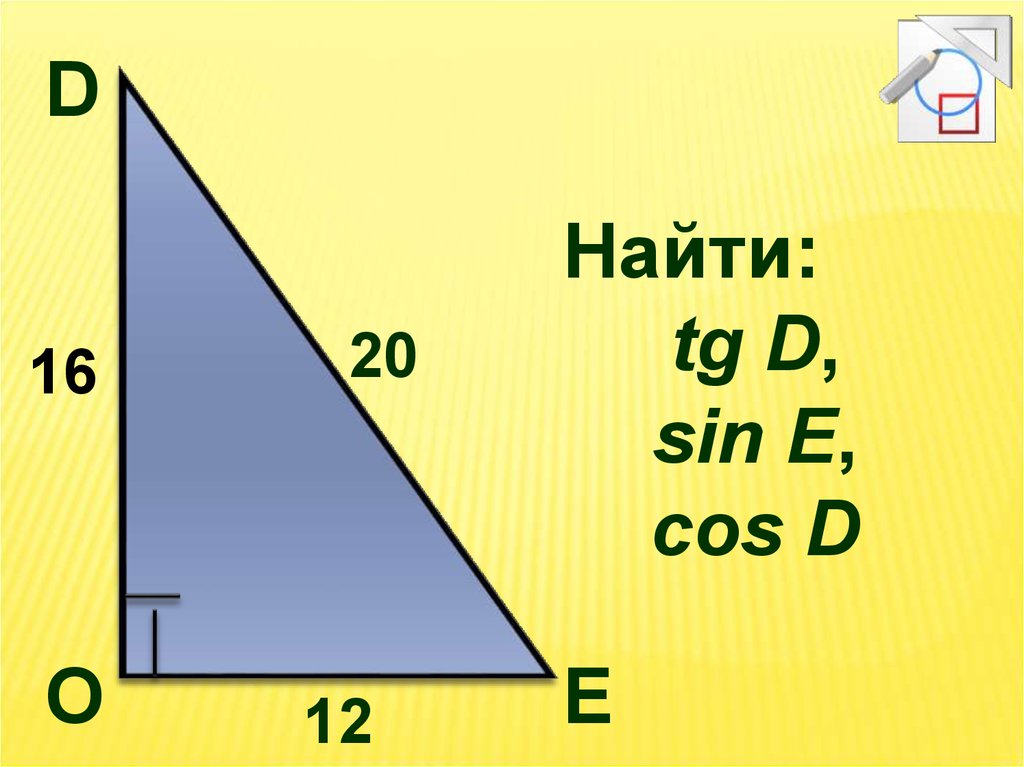
11.

D
16
O
20
12
Найти:
tg D,
sin E,
cos D
E

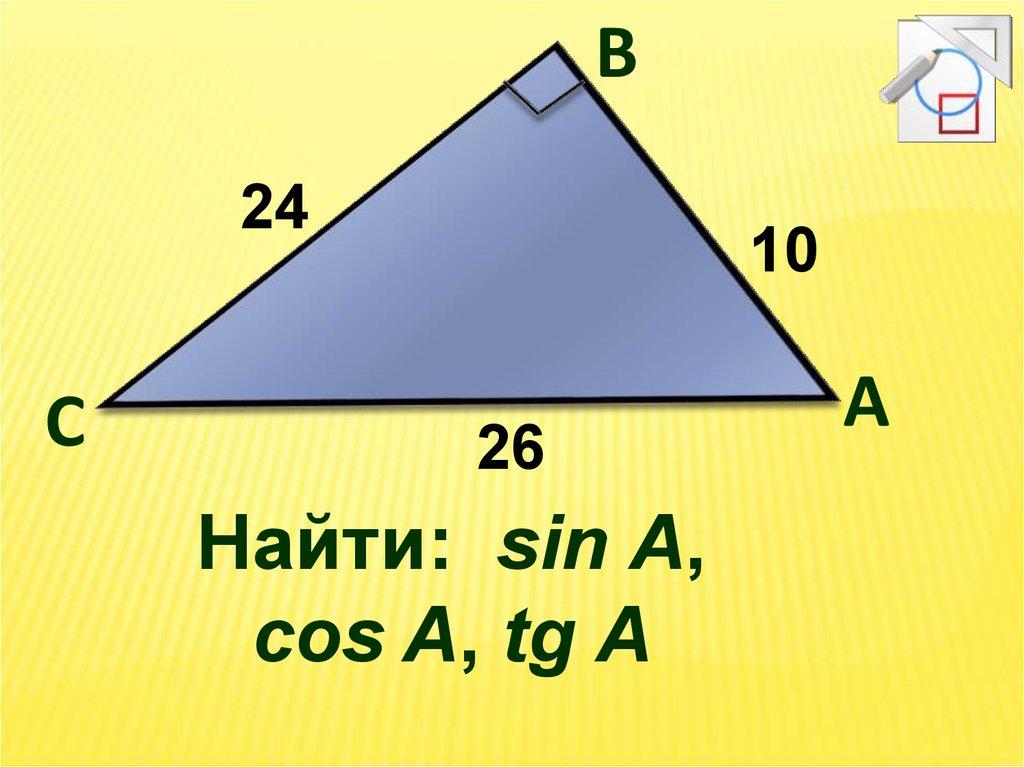
12.

B
24
C
10
26
Найти: sin A,
cos A, tg A
A

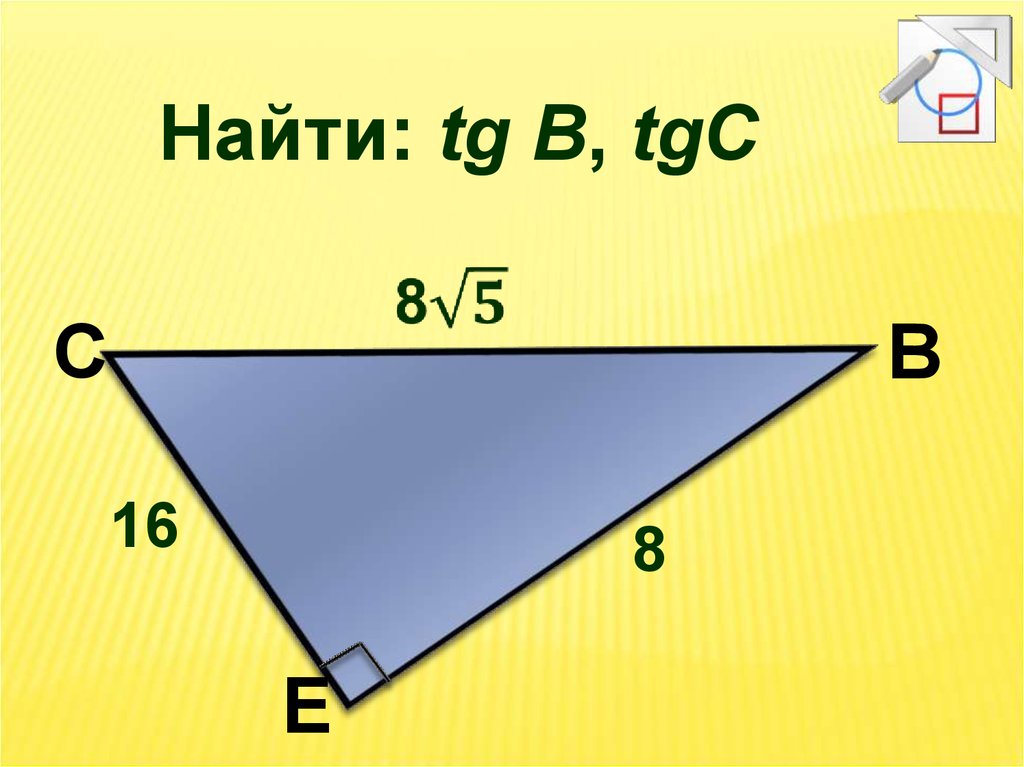
13.

Найти: tg В, tgС
С
В
16
8
Е

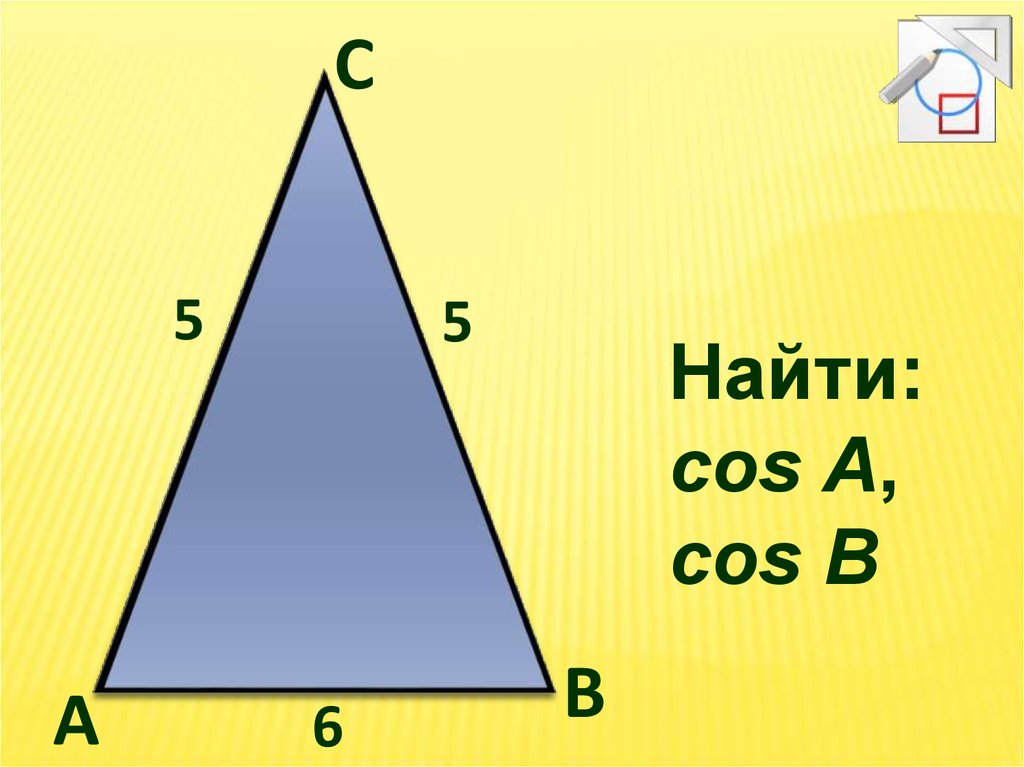
14.

C
5
A
5
6
Найти:
cos A,
cos B
B

15.

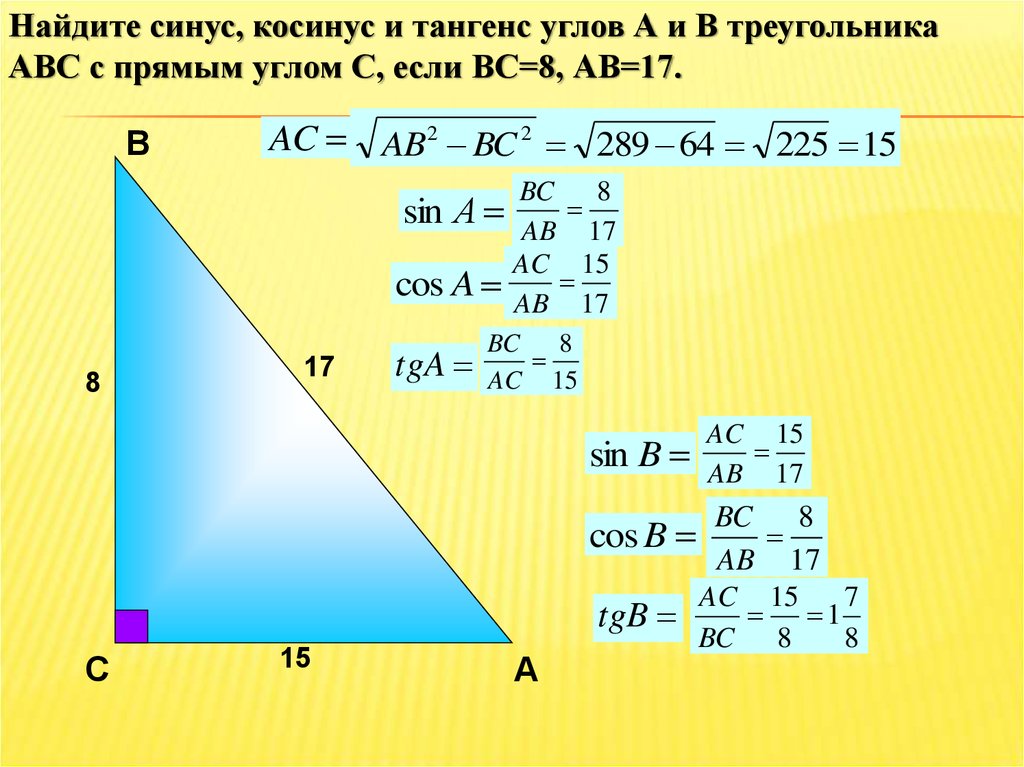
Найдите синус, косинус и тангенс углов А и В треугольника
АВС с прямым углом С, если ВС=8, АВ=17.
В
AC AB2 BC 2 289 64 225 15
sin А
cos A
8
17
tgA
BC
8
AB 17
AC 15
AB 17
BC
8
AC 15
sin B
AC 15
AB 17
BC
8
cos B
AB 17
tgB
С
15
А
AC 15
7
1
BC 8
8

16.

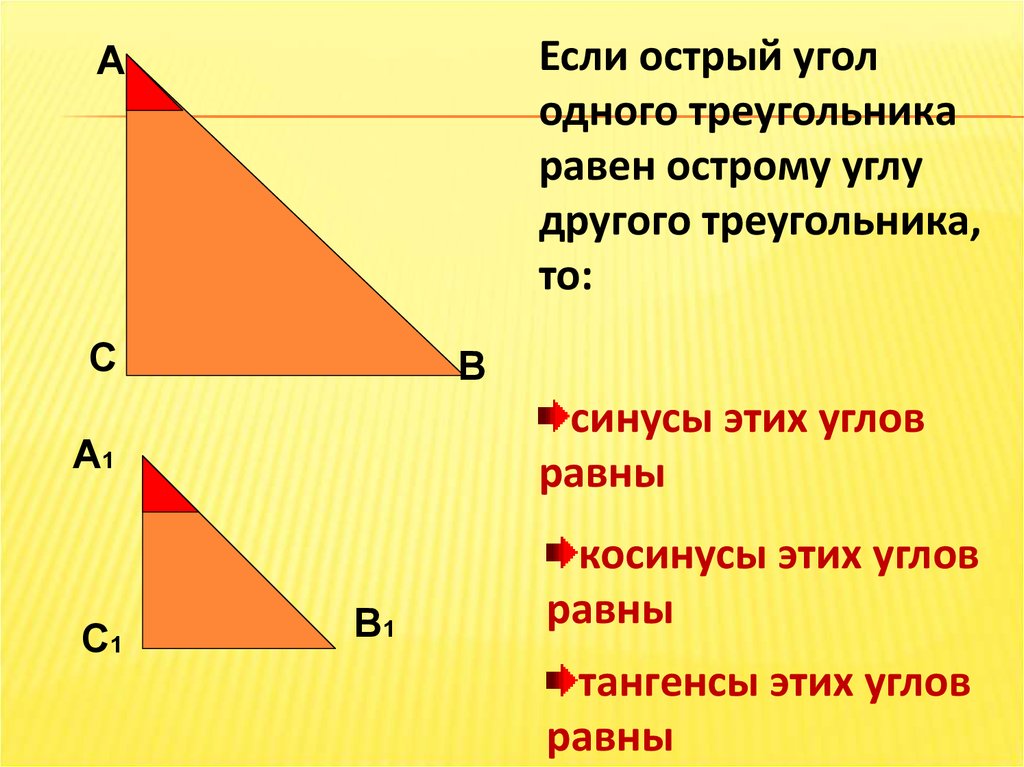
Если острый угол
одного треугольника
равен острому углу
другого треугольника,
то:
А
С
В
синусы этих углов
равны
А1
С1
В1
косинусы этих углов
равны
тангенсы этих углов
равны

17.

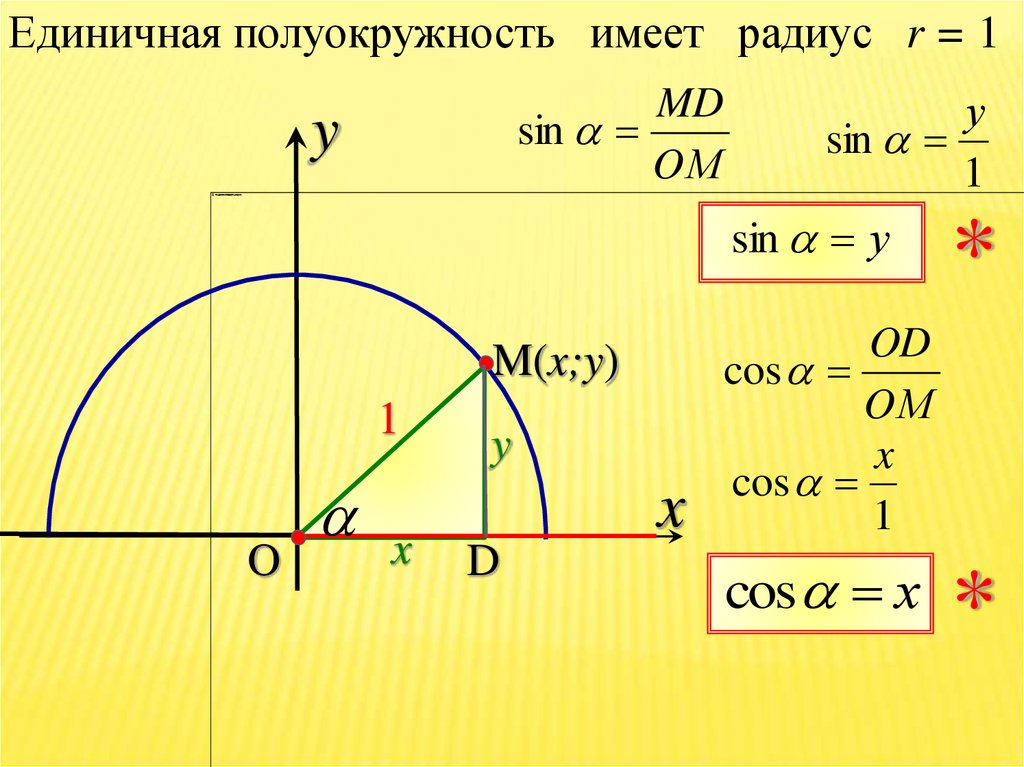
Единичная полуокружность имеет радиус r = 1
MD
sin
OМ
y
у
sin
1
sin у
M(x;y)
1
O
x
y
x
D
*
OD
cos
OМ
x
cos
1
cos х
*

18.

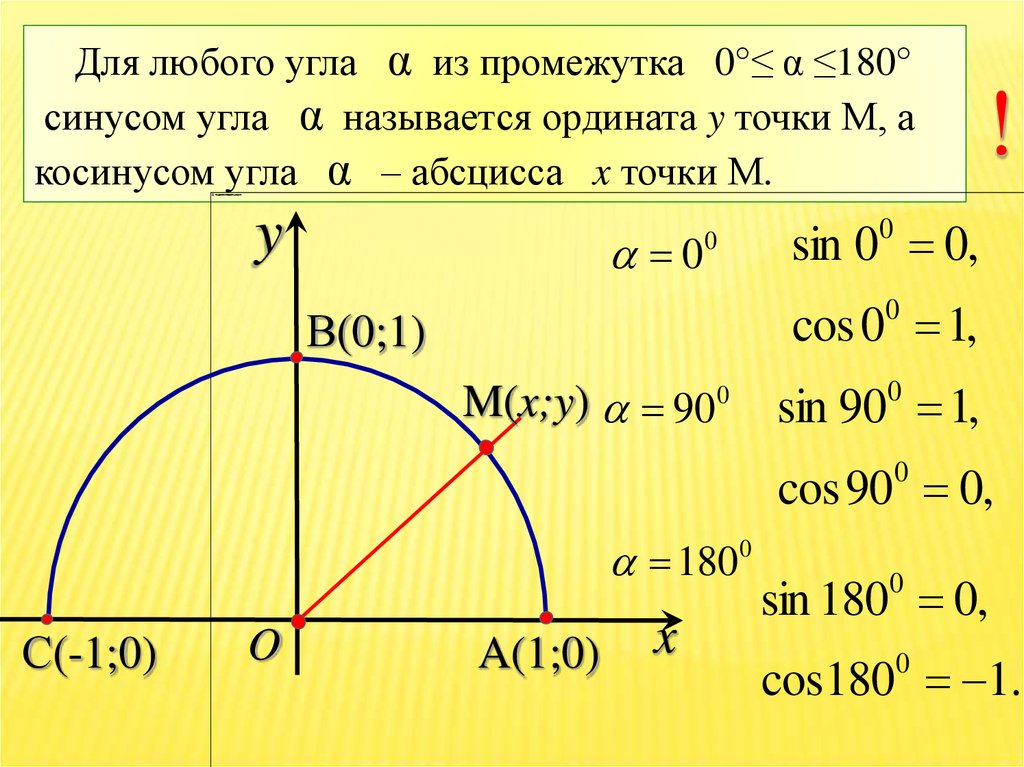
Для любого угла α из промежутка 0°≤ α ≤180°
синусом угла α называется ордината y точки М, а
косинусом угла α – абсцисса x точки М.
y
0
!
sin 0 0,
0
0
cos 0 1,
0
В(0;1)
sin 90 1,
M(x;y) 900
0
cos 90 0,
0
180
С(-1;0)
O
A(1;0)
x
0
sin 1800 0,
cos180 1.
0

19.

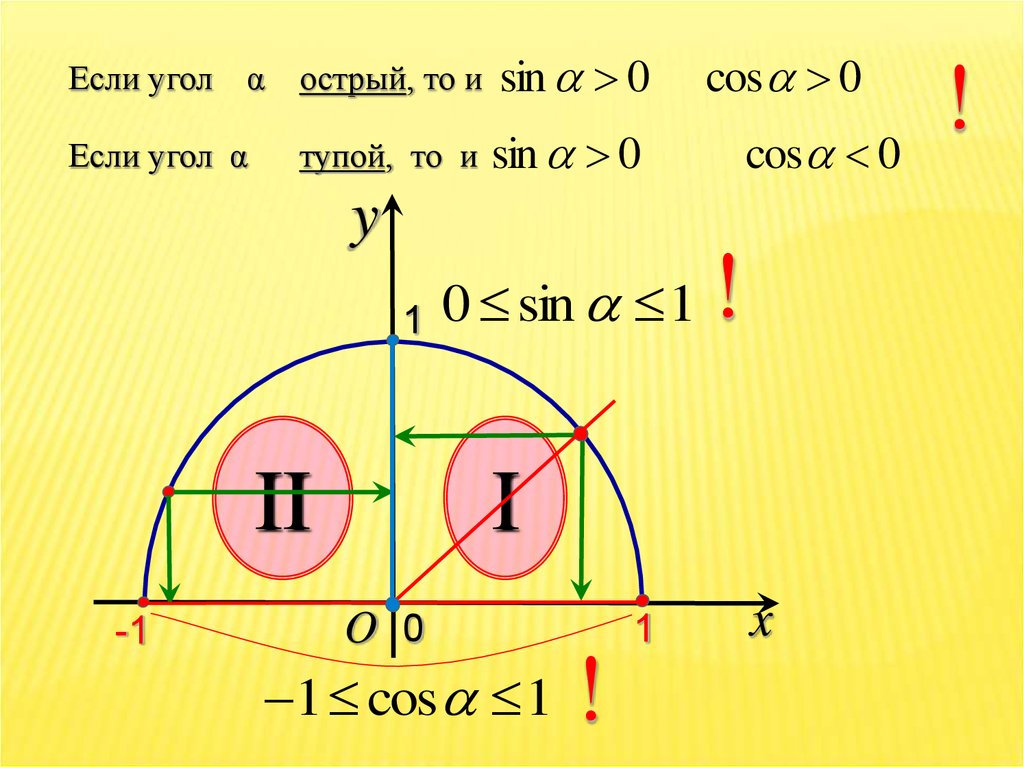
Если угол α
острый, то и
sin 0
Если угол α
тупой, то и
sin 0
cos 0
cos 0
y
1
II
-1
0 sin 1
!
I
O 0
1 cos 1
1
!
x
!

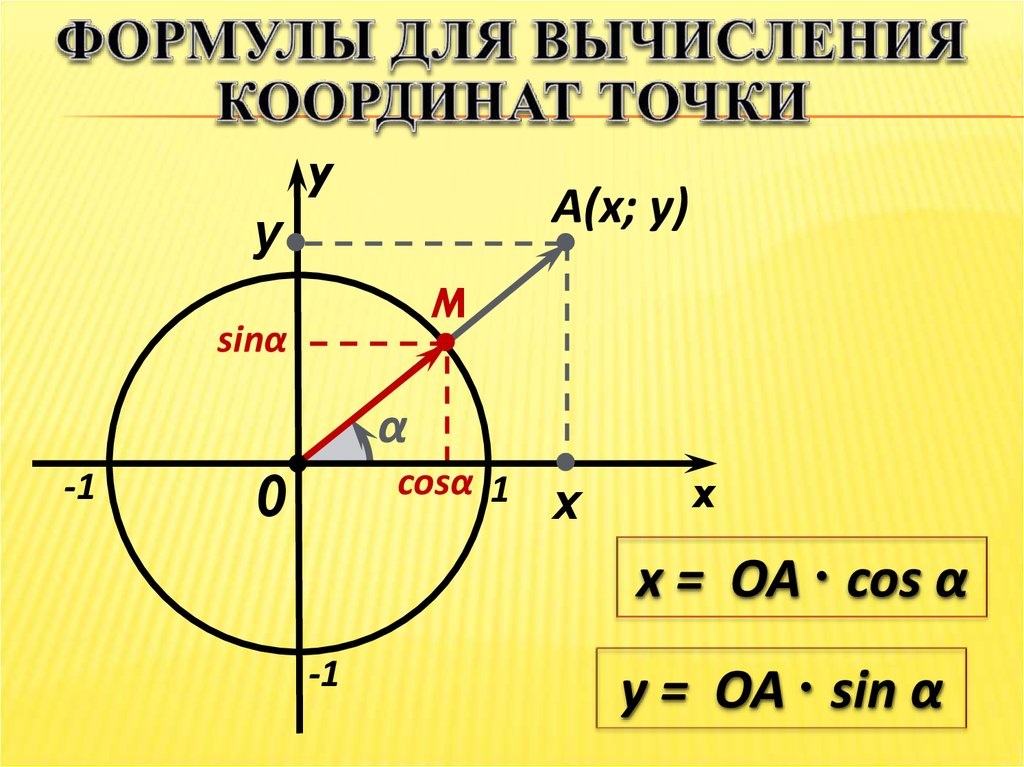
20. Формулы для вычисления координат точки

y
А(х; у)
y
M
sinα
α
-1
0
cosα 1
х
x
x = ОА ∙ cos α
-1
y = ОА ∙ sin α

21.

Основное
тригонометрическое
тождество.
Формулы приведения

22.

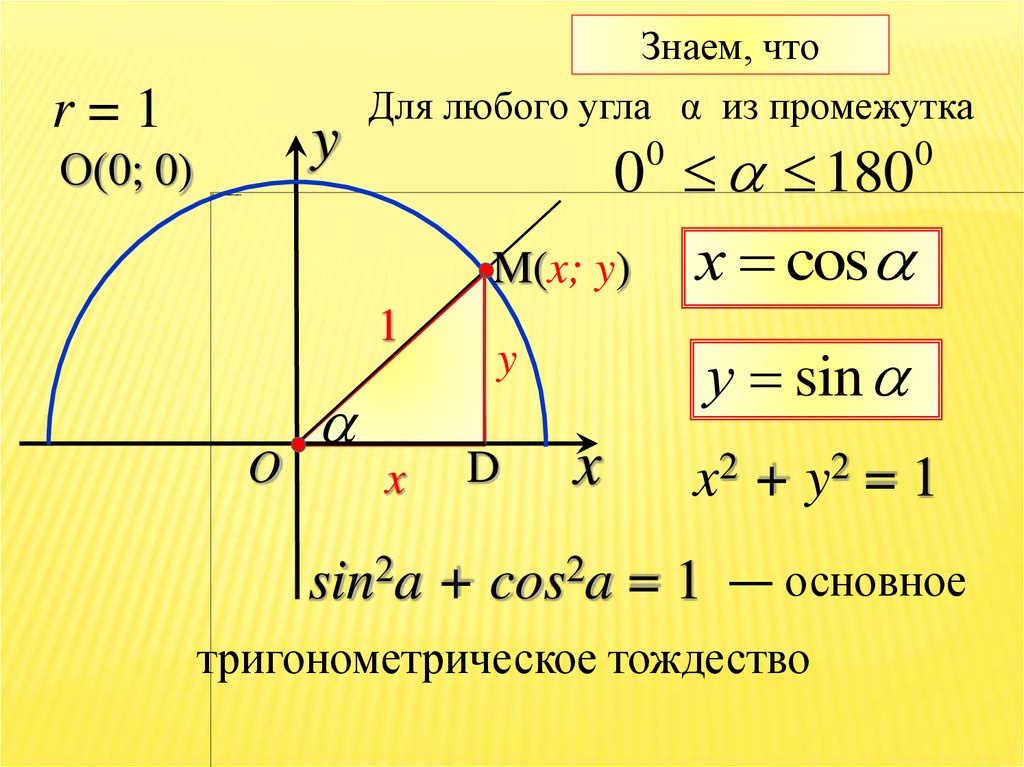
Знаем, что
r=1
y
О(0; 0)
Для любого угла α из промежутка
0 180
0
1
O
x
M(x; y)
х cos
y
у sin
D
x
0
x2 + y2 = 1
sin2a + cos2a = 1 ― основное
тригонометрическое тождество

23.

Используем основное тригонометрическое
тождество для определения положения точки
M ( x; y )
в прямоугольной системе координат
х cos
у sin
sin2a + cos2a = 1
Для любого угла α из промежутка
0 180
0
0

24.

y
1800–
1800
?
x
O
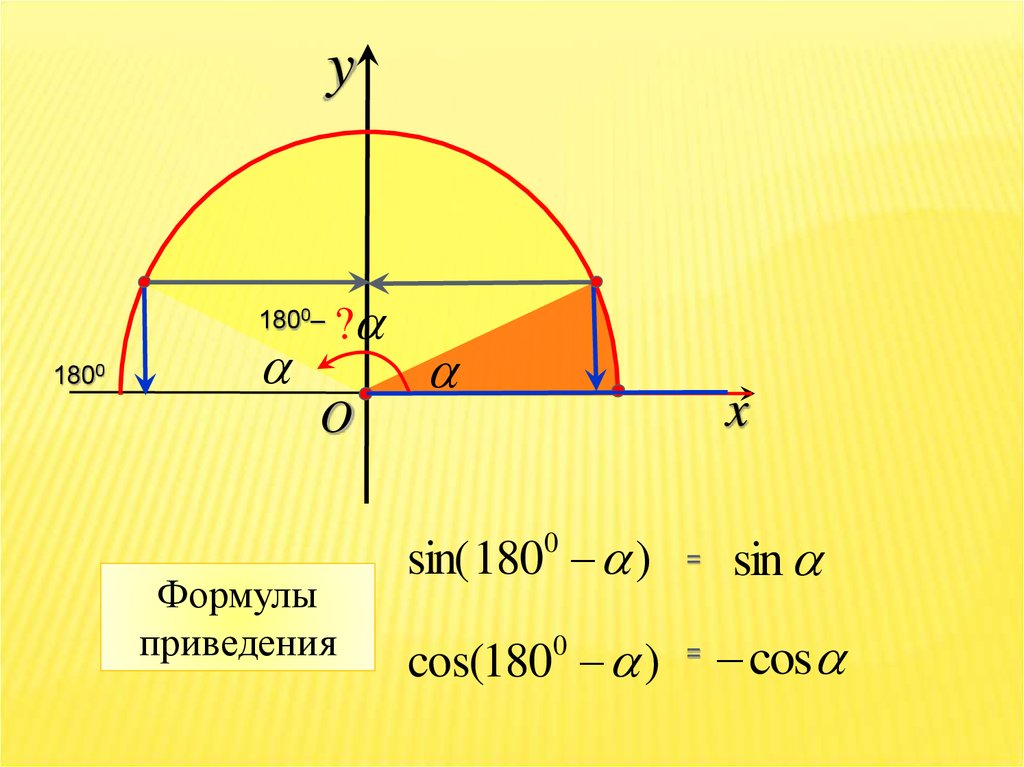
sin( 180 )
=
sin
cos(180 )
=
cos
0
Формулы
приведения
0

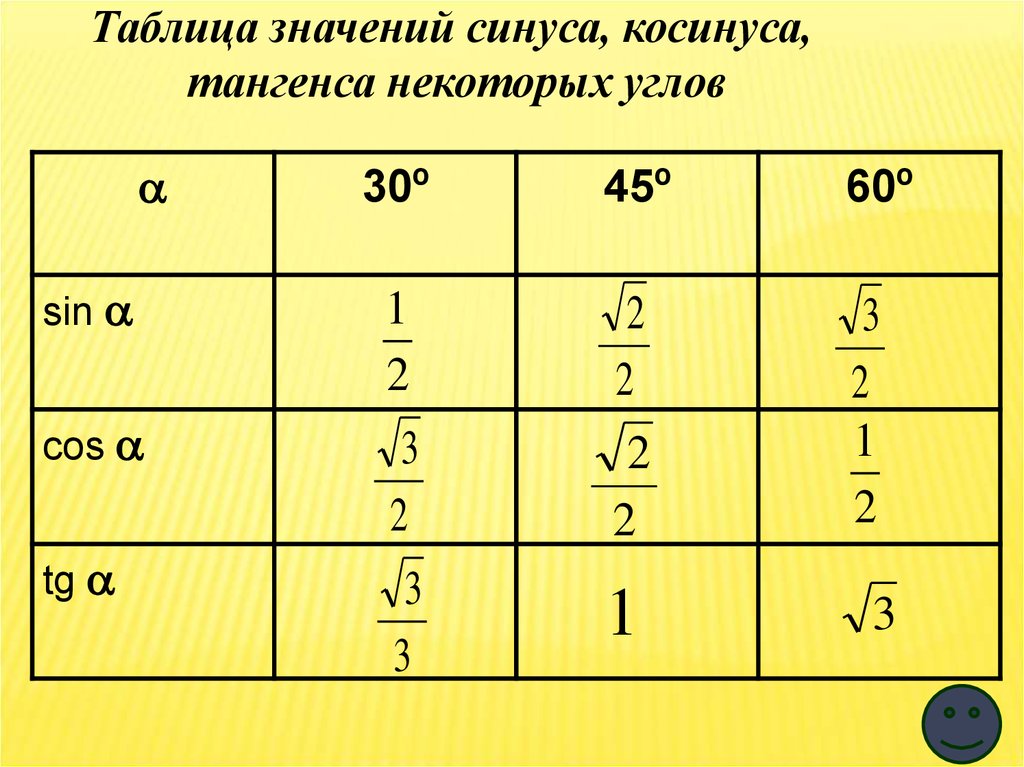
25.

Таблица значений синуса, косинуса,
тангенса некоторых углов
30º
45º
60º
sin
1
2
2
2
cos
3
2
2
2
3
2
1
2
3
3
1
tg
3

26.

Применение формулы
приведения
cos(180 ) = cos
0
1
cos 1200 cos(180 60 ) cos 60
2
0
0
0
Косинус тупого угла равен «–» косинусу смежного с ним
острого угла.
Вычислим быстро!
3
cos 150 cos 30
2
2
0
0
cos 135 cos 45
2
0
0