Соотношения между сторонами и углами треугольника

1. Соотношения между сторонами и углами треугольника

2. Содержание

Повторение (из курса 8 класса)
Диктант
Единичная окружность
Синус, косинус и тангенс угла
Основное тригонометрическое
тождество
• Формулы приведения

3. Повторение

• Соотношения в прямоугольном
треугольнике
• Основное тригонометрическое
тождество
• Значения тригонометрических
функций для углов 30º, 45º, 60º

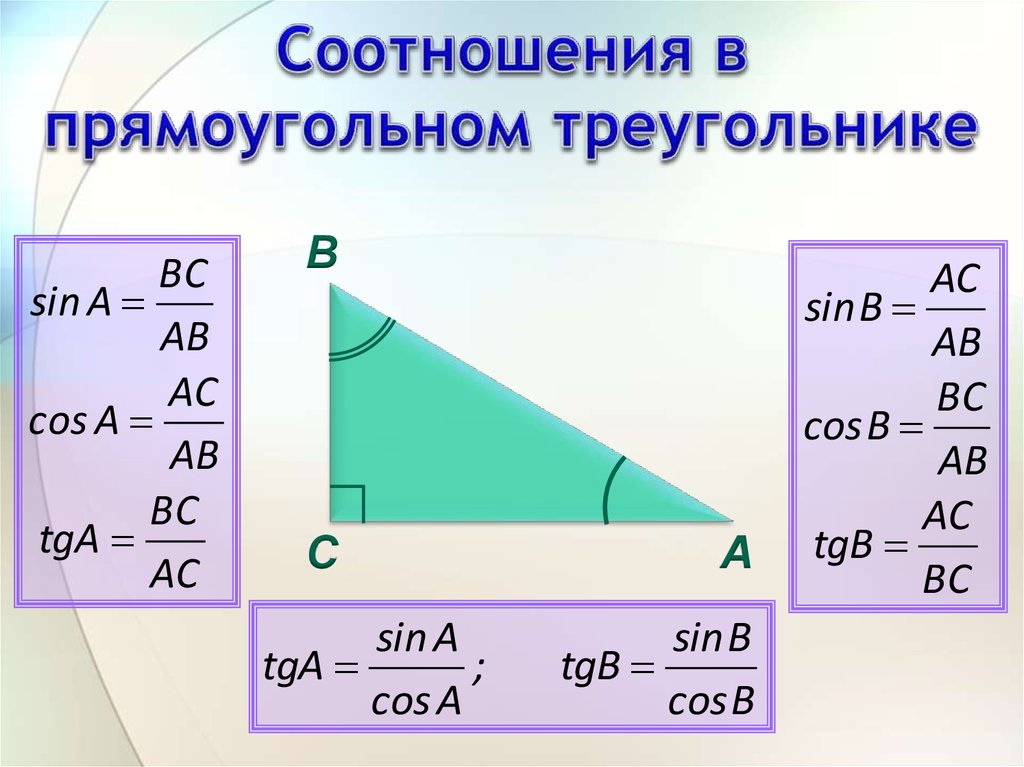
4. Соотношения в прямоугольном треугольнике

B
BC
BC
AC
sin
tgAA
cos
AC
AB
AB
С
А
Тангенсом
Синусом
Косинусом
острого
острого
острогоугла
угла
угла прямоугольного
прямоугольного
прямоугольного
треугольника
треугольника
треугольника называется
называется отношение
отношение
отношение
противолежащего
противолежащего
прилежащего катета
катета
катета
к гипотенузе
ккприлежащему
гипотенузе

5. Соотношения в прямоугольном треугольнике

BC
sin A
AB
AC
cos A
AB
BC
tgA
AC
В
С
sin A
tgA
;
cos A
А
sin B
tgB
cos B
AC
sin B
AB
BC
cos B
AB
AC
tgB
BC

6. Основное тригонометрическое тождество

В
С
sin А cos А 1
2
2
А

7. Соотношения в прямоугольном треугольнике

α
sin α
cos α
В
tg α
60º
30º
С
А
30º
45º
60º
1
2
3
2
3
3
2
2
2
2
3
2
1
2
1
3

8. Единичная окружность

y
N
-1
1
M
0
+
1
K
−
-1
P
x

9.

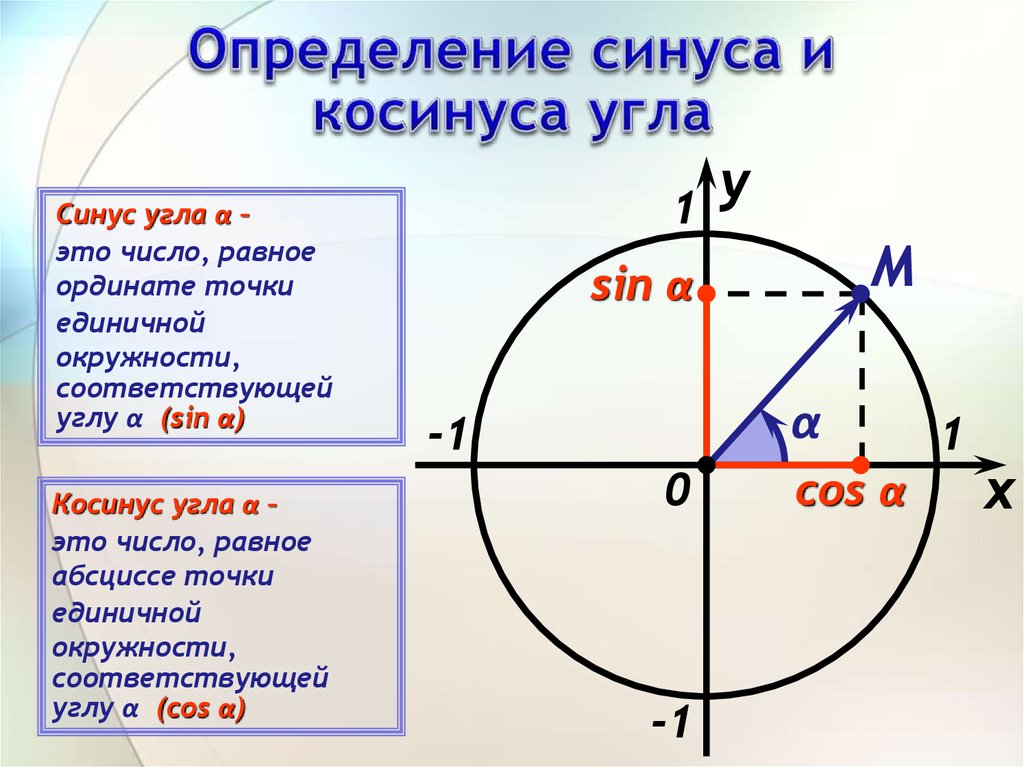
Синус угла α –
это число, равное
ординате точки
единичной
окружности,
соответствующей
углу α (sin α)
Косинус угла α –
это число, равное
абсциссе точки
единичной
окружности,
соответствующей
углу α (cos α)
y
1
M
sin α
α
-1
0
-1
cos α
1
x

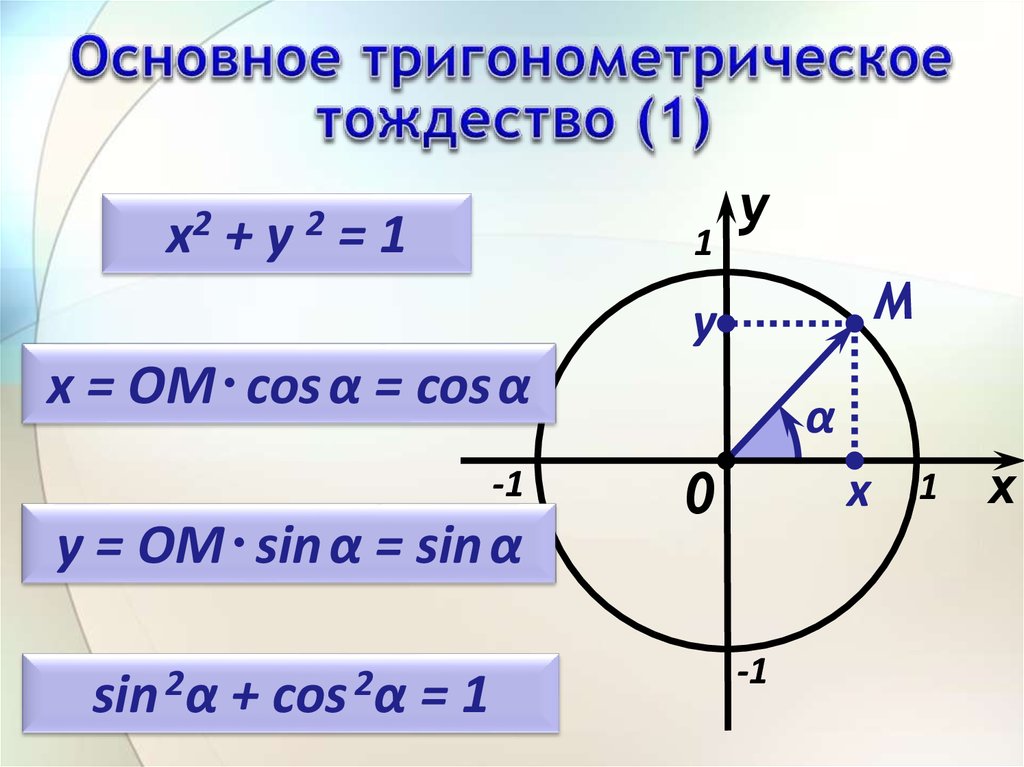
10. Основное тригонометрическое тождество (1)

x2
2
+y =1
1
x = ОM ∙ cos α = cos α
-1
y = ОM ∙ sin α = sin α
sin 2α
+
cos 2α
=1
y
M
y
α
0
x
-1
1
x

11. Формулы приведения

sin (90° – α) = cos α
cos (90° – α) = sin α
sin (180° – α) = sin α
cos (180° – α) = – cos α

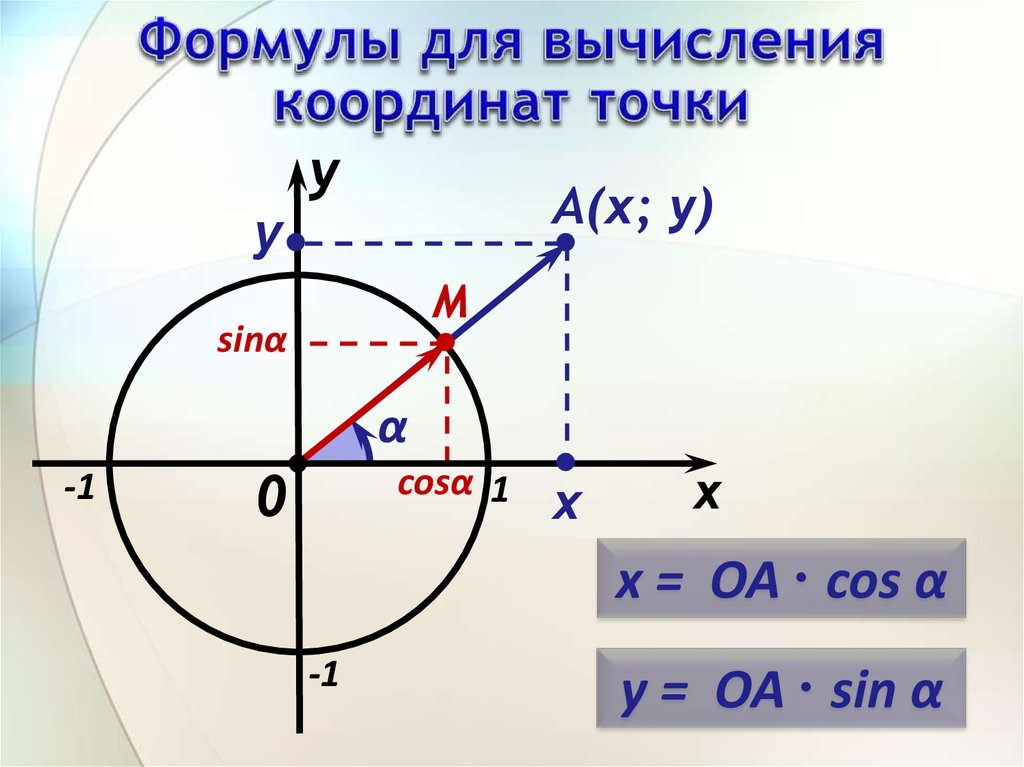
12. Формулы для вычисления координат точки

y
А(х; у)
y
M
sinα
α
-1
0
cosα 1
х
x
x = ОА ∙ cos α
-1
y = ОА ∙ sin α

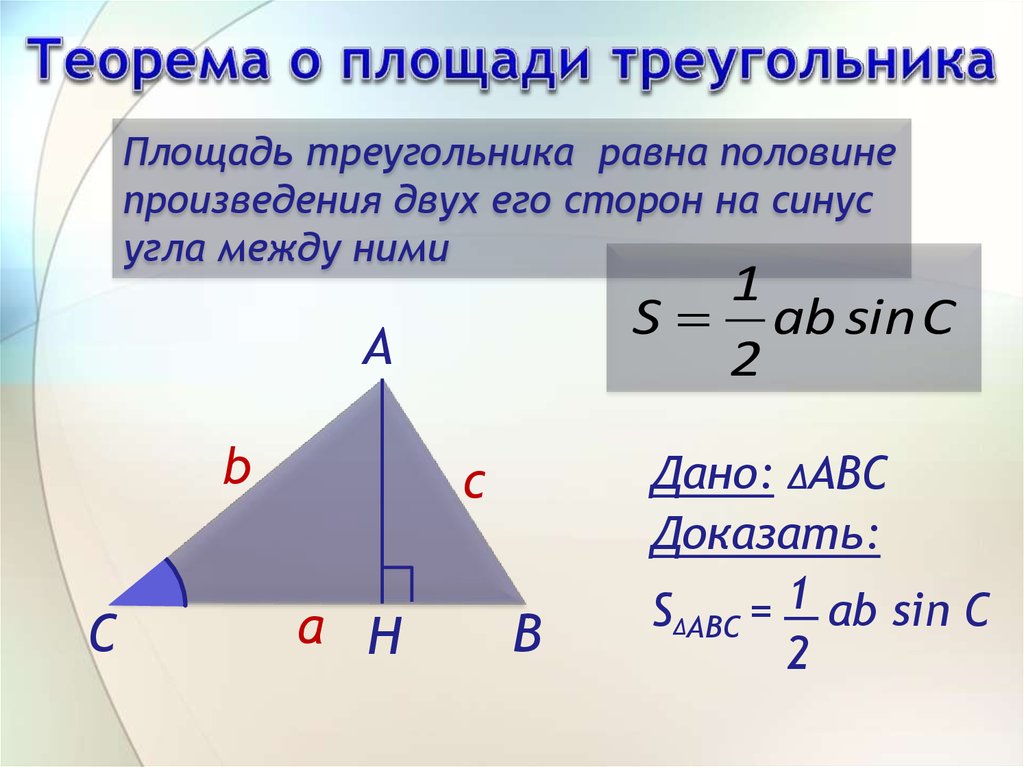
13. Теорема о площади треугольника

Площадь треугольника равна половине
произведения двух его сторон на синус
угла между ними
1
S ab sin C
2
А
b
С
c
a H
В
Дано: ∆АВС
Доказать:
S∆ABC = 1 ab sin C
2

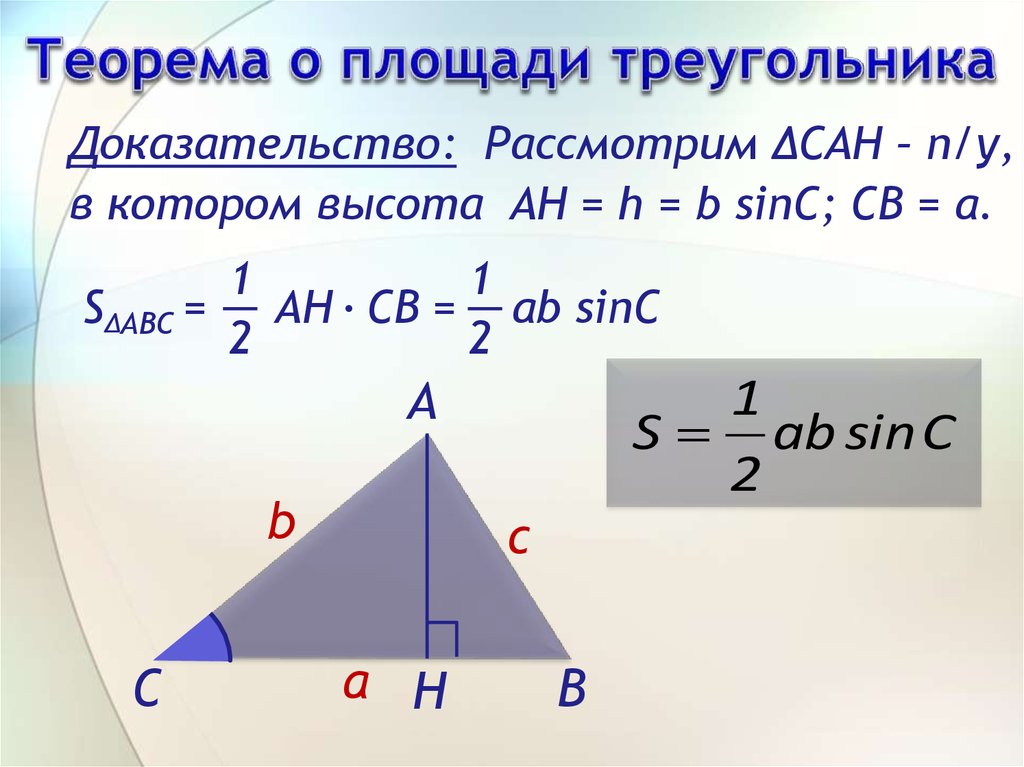
14.

Доказательство: Рассмотрим ∆САН – п/у,
в котором высота AH = h = b sinC; CB = a.
1
1
S∆ABC = AH ∙ CB = ab sinC
2
2
А
b
С
1
S ab sin C
2
c
a H
В

15. Математический диктант

16. Вопрос 1

Стороны
прямоугольного
треугольника равны
9 м, 12 м и 15 м.
Найдите синус
большего острого
угла этого
треугольника.
Стороны
прямоугольного
треугольника равны
6 см, 8 см и 10 см.
Найдите косинус
большего острого
угла этого
треугольника.

17. Вопрос 2

Стороны
прямоугольного
треугольника равны
13 дм, 12 дм и 5 дм.
Найдите тангенс
меньшего острого
угла этого
треугольника.
Стороны
прямоугольного
треугольника равны
26 м, 24 м и 10 м.
Найдите котангенс
меньшего острого
угла этого
треугольника.

18. Вопрос 3

Катет
прямоугольного
треугольника равен
16 см, а
противолежащий
угол равен 45º.
Найдите гипотенузу
этого треугольника.
Гипотенуза
прямоугольного
треугольника равна
24 дм, а один из
острых углов равен
60º. Найдите катет,
прилежащий к
этому углу
треугольника.

19. Вопрос 4

Вычисляя тангенс
острого угла
прямоугольного
треугольника ученик
получил число,
равное 3,14. Верны
ли его вычисления?
Вычисляя синус
острого угла
прямоугольного
треугольника ученик
получил число,
равное 3,14. Верны
ли его вычисления?

20. Вопрос 5

Найдите синус
острого угла, если
его косинус равен 0,8
Найдите косинус
острого угла, если
его синус равен 0,6.

21. Вопрос 6

Косинус острого
угла прямоугольного
треугольника равен
11/25. Чему равен
синус второго
острого угла этого
треугольника?
Синус острого угла
прямоугольного
треугольника равен
6/13. Чему равен
косинус второго
острого угла этого
треугольника?

22. Проверка

1. 0,8
1. 0,6
2. 5/12
2. 2,4
3. 16√2
3. 12
4. Да
4. Нет
5. 0,6
5. 0,8
6. 11/25
6. 6/13