Similar presentations:
Соотношение между сторонами и углами треугольника. Решение задач
1.
8 классЛ.С. Атанасян
Геометрия 7-9
2.
«Образование –это не количество прослушанных
уроков, а количество понятых.
Так что, если хотите идти вперед,
то поспешайте медленно и
будьте внимательны»
3.
Как называются стороныпрямоуголь ного треугольни ка?
АВ – гипотенуза
ВС – катет, противолежащий углу А
АС – катет, прилежащий углу А
4.
Синус (sin)Синусом острого угла
называется отношение
гипотенузе.
прямоугольного треугольника
противолежащего катета к
BC
sin A
AB
5.
Косинус (cos)Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
AC
cos A
AB
6.
Тангенс (tg)Тангенсом острого угла прямоугольного треугольника
называется отношение противолежащего катета к
прилежащему.
BC
tgA
AC
7. Тригонометрические тождества
1)Основное тригонометрическое тождество:
sin A cos A 1
2
2
2) Тангенс угла равен отношению синуса к
косинусу этого угла.
sin A
tgA
cos A
8.
Выберите верное утверждение:1.Синусом острого угла прямоугольного
треугольника называется
Л
- отношение прилежащего катета к гипотенузе.
Н
-отношение противолежащего катета к
прилежащему.
А
-отношение противолежащего катета к
гипотенузе.
B
C
А
9.
Выберите верное утверждение:2.Косинусом острого угла
прямоугольного треугольника
называется
Ф -отношение противолежащего катета
к гипотенузе.
Р - отношение прилежащего катета к
гипотенузе.
О - отношение противолежащего катета
к прилежащему.
B
C
А
10.
Выберите верное утверждение:3.Тангенсом острого угла прямоугольного
треугольника называется
B
C
З -отношение противолежащего катета к гипотенузе
Н -отношение прилежащего катета к
противолежащему
-отношение противолежащего катета к
Х
прилежащему
А -отношение прилежащего катета к гипотенузе
А
11.
Выберите верное утверждение:B
4. Тангенс угла равен
Д
-синусу этого угла
C
И
-отношению синуса к косинусу этого угла
Г
-отношению косинуса к синусу этого угла
П
-косинусу этого угла
А
12.
Выберите верное утверждение:5.Равенство
sin 22 A cos 22 A 1
называют
Г -формулой квадрата суммы
М -основным тригонометрическим тождеством
B
Ф - формулой суммы квадратов
C
А
13.
Выберите верное утверждение:6. Катет, противолежащий углу α равен
У
-произведению гипотенузы на тангенс угла α
М
-произведению гипотенузы на косинус угла α
Е
-произведению гипотенузы на синус угла α
B
α
C
А
14.
Выберите верное утверждение:7. Катет, прилежащий к углу α равен
Д -произведению гипотенузы на косинус угла α
Э -произведению гипотенузы на синус угла α
Ю -произведению гипотенузы на тангенс угла α
B
C
α
А
15. Какое слово вы получили?
проверка:А
Р
Х
И
М
Е
Д
16.
Соотношения между сторонами иуглами прямоугольного
треугольника
C
b
A
sin
a
В
c
cos
a
c
b
c
a
tg
b
17. Тригонометрические тождества
1)Основное тригонометрическое тождество:
sin A cos A 1
2
2
2) Тангенс угла равен отношению синуса к
косинусу этого угла.
sin A
tgA
cos A
18. Задача 1. (в паре )
17
Задача 1. (в паре )
В
1
а) Дано: sinα=
7
Найти: cosα и tgα.
α
А
С
19. Решение:
а).1. По основному тригонометрическому тождествуsin cos 1
2
cos 1 sin
1
1
7
2
48 4 3
49
7
sin
1 4 3
1 7
1
3
tg
:
.
cos
7 7
7 4 3 4 3 12
2
2.
2
Ответ:
4
3
7
3
,
.
12
20. Задача 2.(с/о)
17
Задача 2.(с/о)
б)Дано: cosα=
1
В
10
Найти: sinα и tgα.
α
А
С
21. Решение:
а).1. По основному геометрическому тождествуsin
2
cos 1
2
2
sin 1 cos
2
2.
9
3 3 10
1
1
10
10 10
10
sin 3 10 1
3 10 10
tg
:
3
10
cos
10
10
3 10
Ответ :
,3.
10
22.
Задача 3(устно). Дано: АВСД- трапеция,АВ=ДС, ВС=6, АД=12, sin A=0,8.
Найти: АВ.
6
В
С
?
А
M
К
12
D
23.
1. АМ=КД=(АД-MK):2=(12-6):2=32. По основному тригонометрическому тождеству
1 0,82 1 0,64 0,36 0,6
AM
AM
30
3
cos A
, AB
5
AB
cos A
6
0,6
В
cos A 1 sin 2 A
3.
Ответ : 5.
5
sin A 0,8
А
3
M
24.
ПовторениеC
Соотношения между сторонами и
углами прямоугольного
треугольника.
a
b
В
A
c
Теорема Пифагора.
2
a
+
2
b =
2
c
25. Задача 4.(с/о)
Дано: ∆АСВ прямоугольный, уголАСВ=90º, АС=8 см, СВ= 6
см.
Найти: cos A, sin A, tg A,
ctg A
А
8
С
6
В
26. Решение(1 способ):
1. Таккак ∆АВС –прямоугольный, то по
теореме Пифагора
АВ2=АС2+СВ2.
AB AC 2 CB 2 8 2 6 2 100 10 см
=
2.
AC 8 4
cos A
AB 10 5
CB 6 3
tgA
AC 8 4
CB 6 3
sin A
AB 10 5
4 3 3
,
,
Ответ:
5 5 4
27. Решение(2 способ):
CB 6 31). sin A
AB 10 5
2). cos 1 sin
2
3
1
5
2
16 4
25 5
sin A 3 4 3
3).tgA
:
cos A 5 5 4
4 3 3
,
,
Ответ:
5 5 4
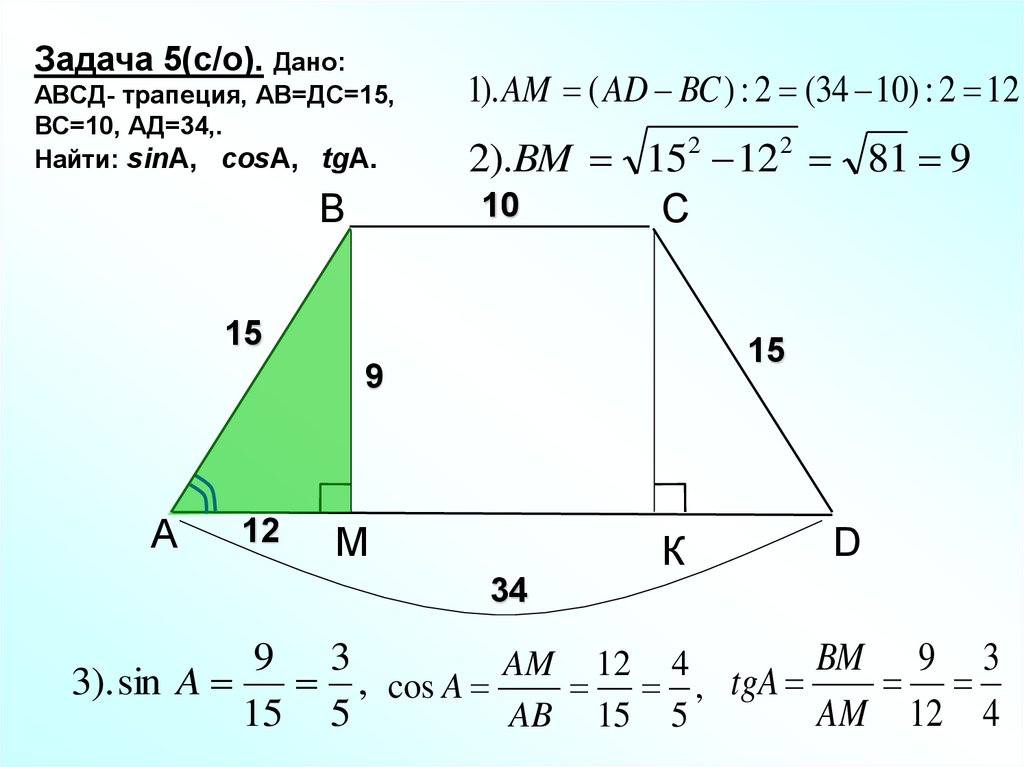
28.
Задача 5(с/о). Дано:АВСД- трапеция, АВ=ДС=15,
ВС=10, АД=34,.
Найти: sinA, cosA, tgA.
В
1). AM ( AD BC ) : 2 (34 10) : 2 12
2).BM 152 122 81 9
10
С
15
15
9
А
12
M
К
D
34
9 3
BM 9 3
AM 12 4
3). sin A
, cos A
, tgA
15 5
AM 12 4
AB 15 5
29.
300 450 600sin
cos
tg
1
2
2
2
3
2
2
2
1
3
1
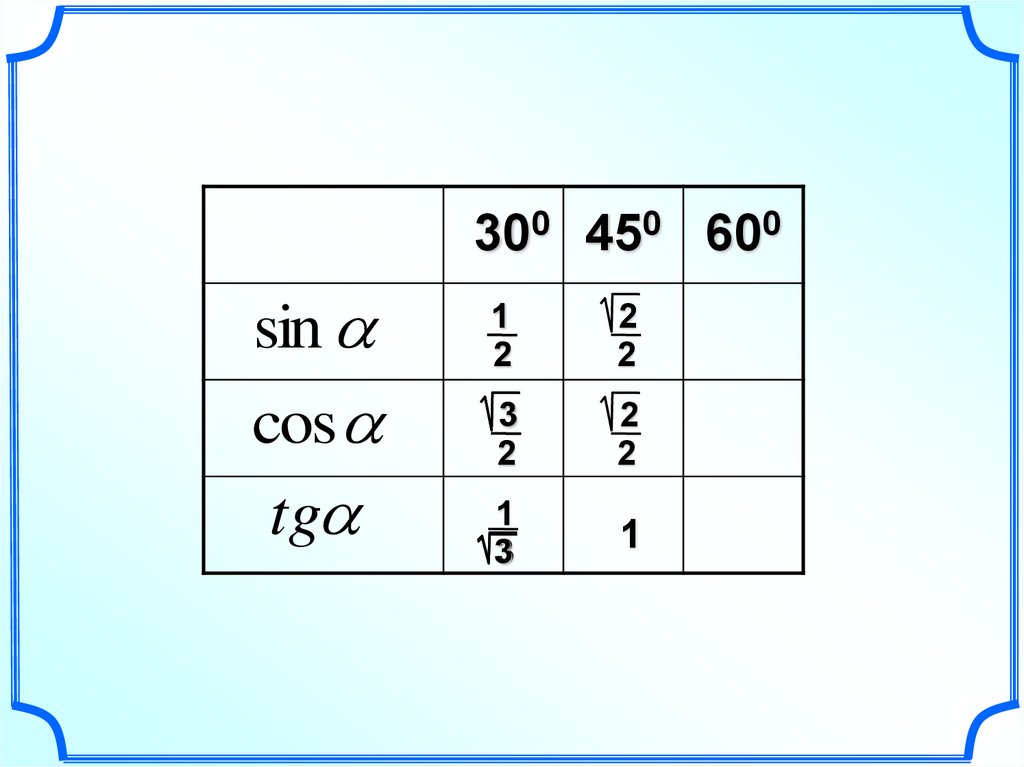
30.
300 450 600sin
cos
tg
1
2
2
2
3
2
3
2
2
2
1
2
3
3
1
3
31. Задача 6.(в паре)
Дано: АВСД- прямоугольник, АС=10,Найти:
S АВСД
?
В
С
10
?
60
А
Д
ВАС 60
32. Решение (1 способ):
1. АСВ 90 - 60 30 , АВ АС : 2 10 : 2 52. ВС 102 52 75 5 3
3. S АВ ВС 5 5 3 25 3
5 3
В
10
5
А
60
С
Ответ : 25 3
Д
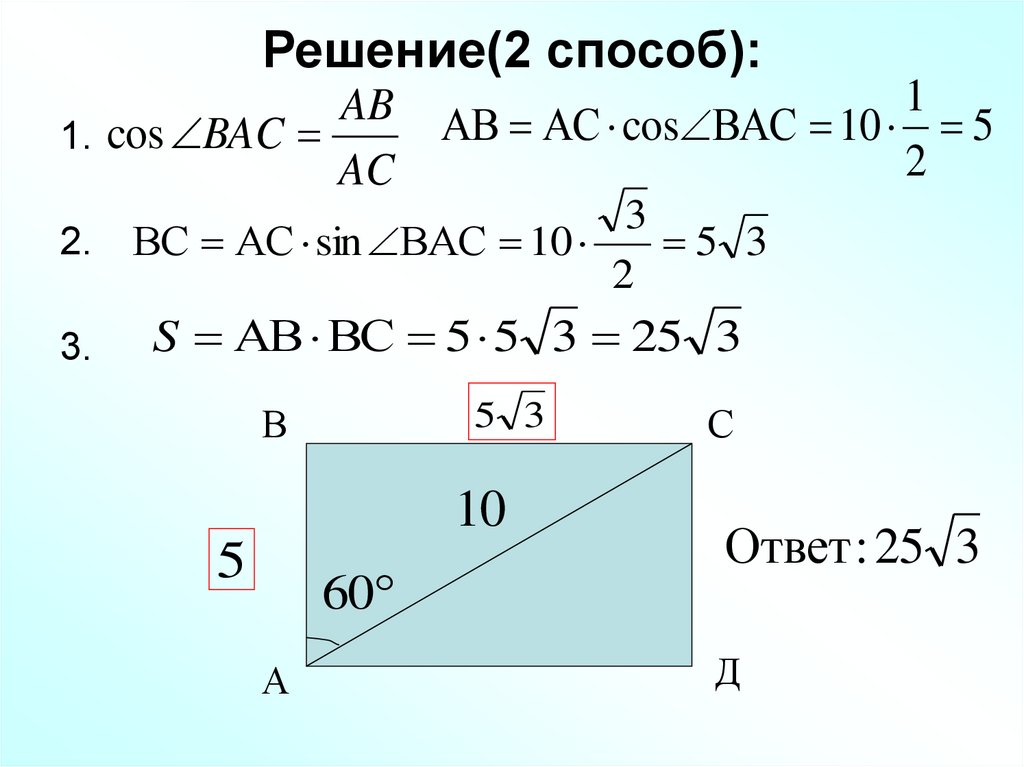
33. Решение(2 способ):
AB1. cos BAC
AC
1
АВ АС cos ВАС 10 5
2
3
2. ВС АС sin ВАС 10
5 3
2
3.
S АВ ВС 5 5 3 25 3
5 3
В
10
5
60
А
С
Ответ : 25 3
Д
34.
ПовторениеПропорциональные
отрезки в прямоугольном
треугольнике
C
b
A
a
h
bc
a
c
В
c
h bc ac b bc c
a ac c
35.
Задача 7.(устно)
Найдите неизвестные линейные элементы
прямоугольного треугольника АВС, ACB 90
C
b АС 18 20
h
b
2 10
a ВС 2 20
6
B
2
6 10
D
18
А
a
c
h DС 18 2
c 18 2 20
36.
Задача 8.(д/з) Найти sinA,cosA, tgA.
h 2 3 6
C
10
А
2
b 2 5 10
6
D
3
B
6
6
3
15
2
10
sin A
, cos A
, tgA
2
5
5
5
10
10
37.
Задача 9(с/о). Дано: АВСДпрямоугольная трапеция, ВС=8, СД= 2 3 ,Найти: AM , S ABCD .
В
8
С
120
2 3
А
M
D
38.
1). ABM 120 90 302 3 2
BM
3 2 3
4
2). cos ABM
,
, AB
AB
2
AB
3
Решение:
В
8
С
120
30
2 3
2 3
Ответ : 20 3
8
А
3).S ABCD
4
M
12
BC AD
BM
2
D
8 12
2 3 20 3
2
39.
ПовторениеСоотношения между сторонами и
углами прямоугольного
треугольника
C
b
A
a
h
bc
a2 + b2 = c2
a
c
В
c
h bc ac
b bc c
a
sin
c
b
cos
c
a
tg
b
a ac c
40.
Задание на дом:п. 66,67. 1).Придумать и решить
задачу с
использованием основного тригонометрического тождества
и определения синуса, косинуса или тангенса.2). Дан
прямоугольный ∆АСВ , угол АСВ=90º, СД - высота, АД=2 см, ДВ=
3 см.
Найти: cos A, sin A, tg A, ctg A
2). Знания в быту. (задача)
Для постройки лестницы на второй этаж требуется купить доски в
количестве, равном количеству ступенек. Подсчитайте, какое
количество досок необходимо купить, если известно, что высота
между этажами равна 3 метра, угол наклона лестницы равен 30°,
а расстояние между ступеньками 0,25 м.
41.
Закончи предложение:Сегодня на уроке я запомнил……..
Я научился…………………….
Я понял……………………………
У меня не
получилось…………………..
Мне хотелось
бы……………………………
Я справлюсь с домашней работой






































 mathematics
mathematics








