Similar presentations:
Центральные и вписанные углы. 8 класс. Часть 3
1.
Геометрия 8 классЧасть 3
Учитель математики
МОУ “Оленовская школа №2
Волновахского района”
Прохоренко Ирина Ивановна
2.
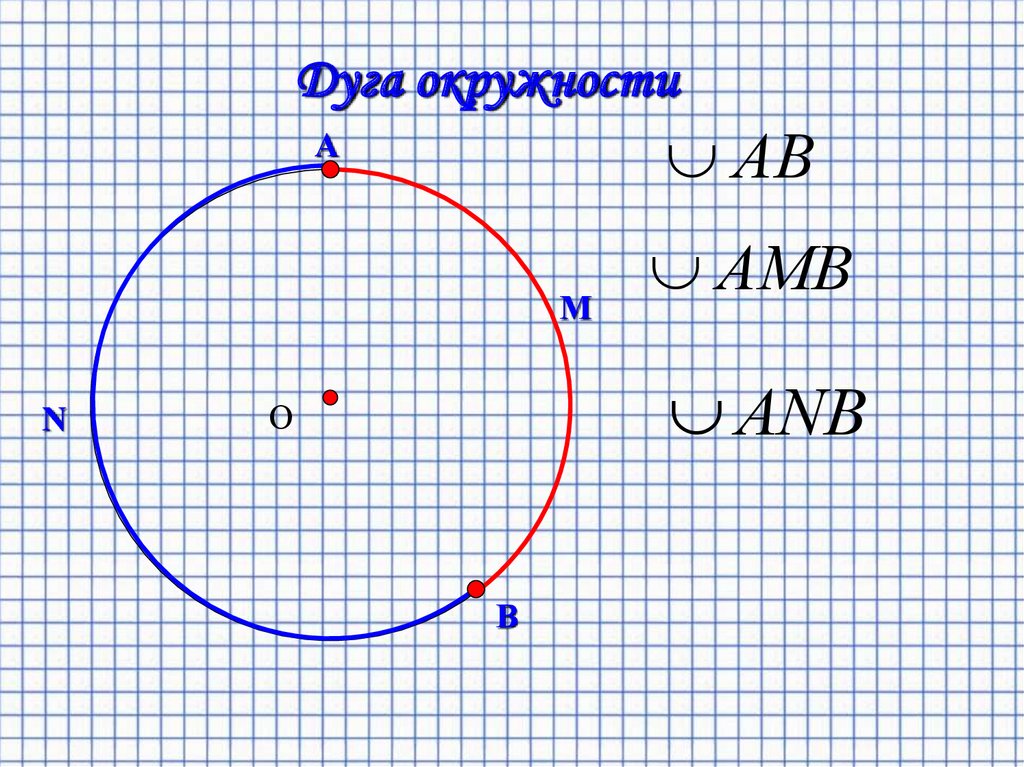
Дуга окружностиАВ
А
М
N
АМВ
АNВ
О
В
3.
Дуга называется полуокружностью, если отрезок,соединяющий ее концы, является диаметром
окружности.
А
d
О
В
4.
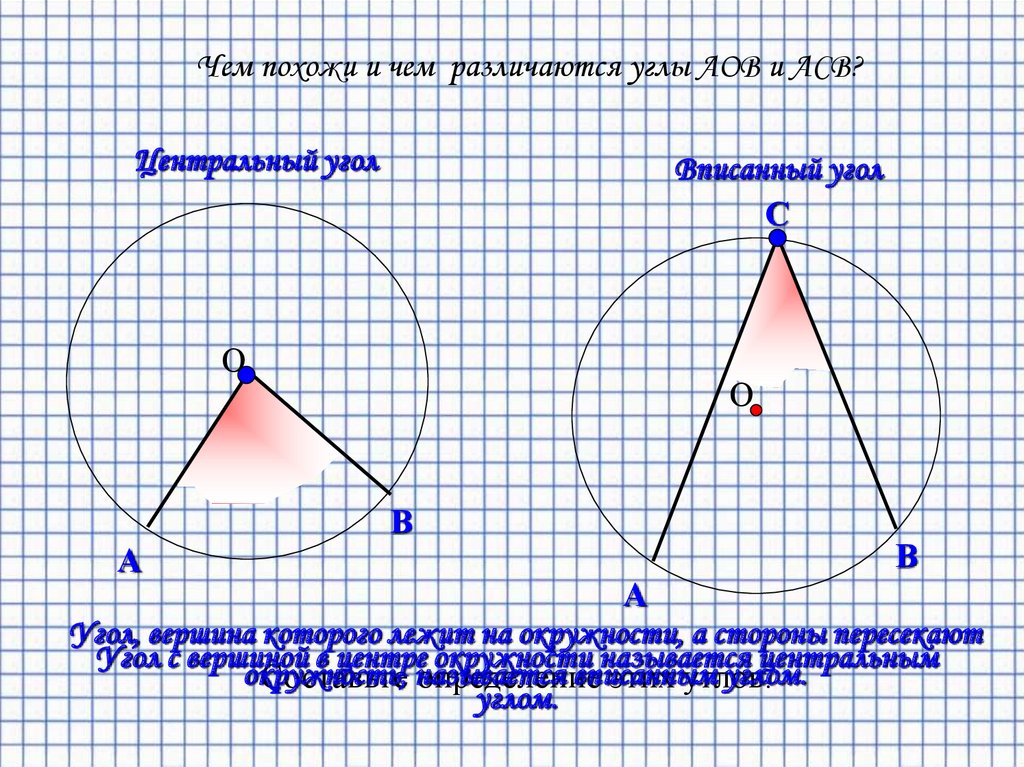
Чем похожи и чем различаются углы АОВ и АСВ?Центральный угол
Вписанный угол
С
О
О
В
А
В
А
Угол, вершина которого лежит на окружности, а стороны пересекают
Угол с вершиной в центре окружности называется центральным
окружность,
вписанным
углом.
Составьте называется
определение
этих углов.
углом.
5.
Дугу окружности можно измерять в градусах.Если дуга АВ окружности с центром О
меньше полуокружности или является
полуокружностью, то ее градусная мера
считается равной градусной мере
центрального угла АОВ.
О
650
В
А
АВ АОВ 65
0
6.
АО
В
АВ АОВ 180
0
7.
Если дуга АВ окружности сцентром О больше
полуокружности, то ее градусная
мера считается равной
360 АОВ
0
О
650
В
А
2950
АВ 360 АОВ 360 65 295
0
0
0
0
8.
САВ СОВ 145300
1150
О
В
АDB 360 115 245
0
0
CDB 360 145 215
0
DB 180
0
0
0
0
0
9.
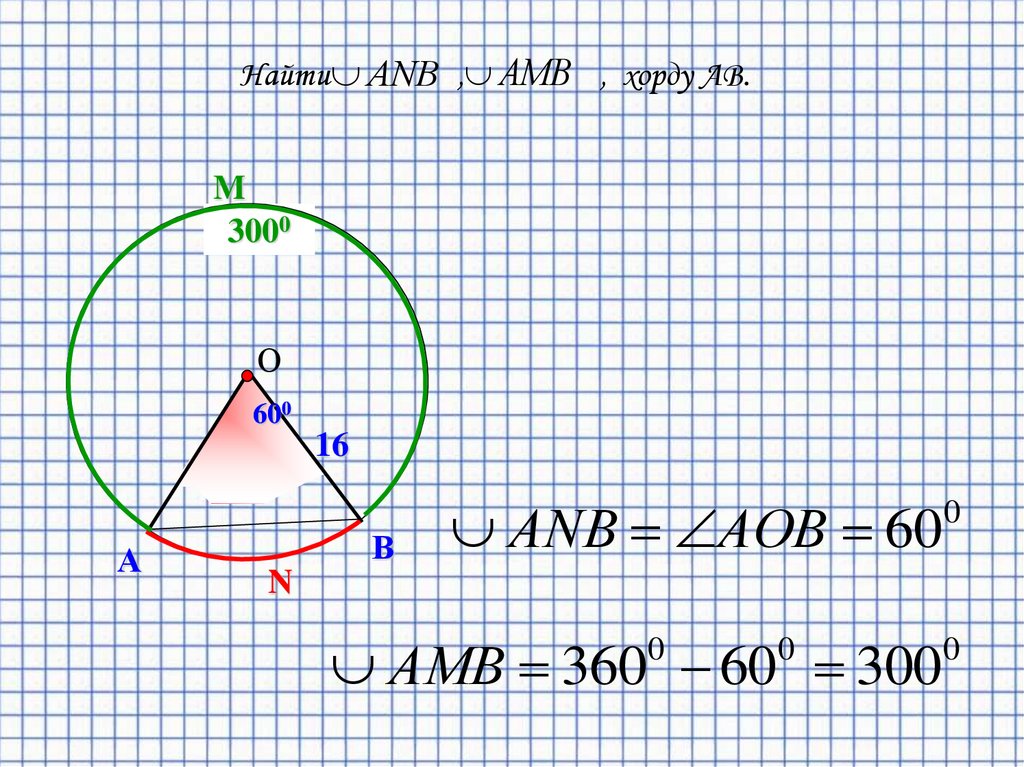
Найти АNВ , АМВ , хорду АВ.M
3000
О
600
16
А
АNВ АОВ 60
0
АMВ 360 60 300
0
В
N
0
0
10.
Найти угол АОВ.M
2720
О
?
В
А
880
11.
Найти расстояние от точки А до радиуса ОВ.6 АВ 600
R = 6.
О
Х
В
600
А
12.
ПовторениеВнешний угол треугольника равен сумме
двух углов треугольника, не смежных с ним.
С
СВК = 1 + 2
2
А
1
В
К
13.
Теорема. Вписанный угол измеряется половинойдуги, на которую он опирается.
В
Дано: АВС – вписанный
1
Доказать: АВС АС
2
a
О
1 случай (О ВС)
a 2a
А
С
В =
a
АС 2a
А р/б В
АВС
=a
Тогда внешний угол АОС = 2a
АС 2a
1
В АС
2
14.
2 случай1
АВD АD
2
+
1
DBC DС
2
В
О
С
А
D
1
АВС АС
2
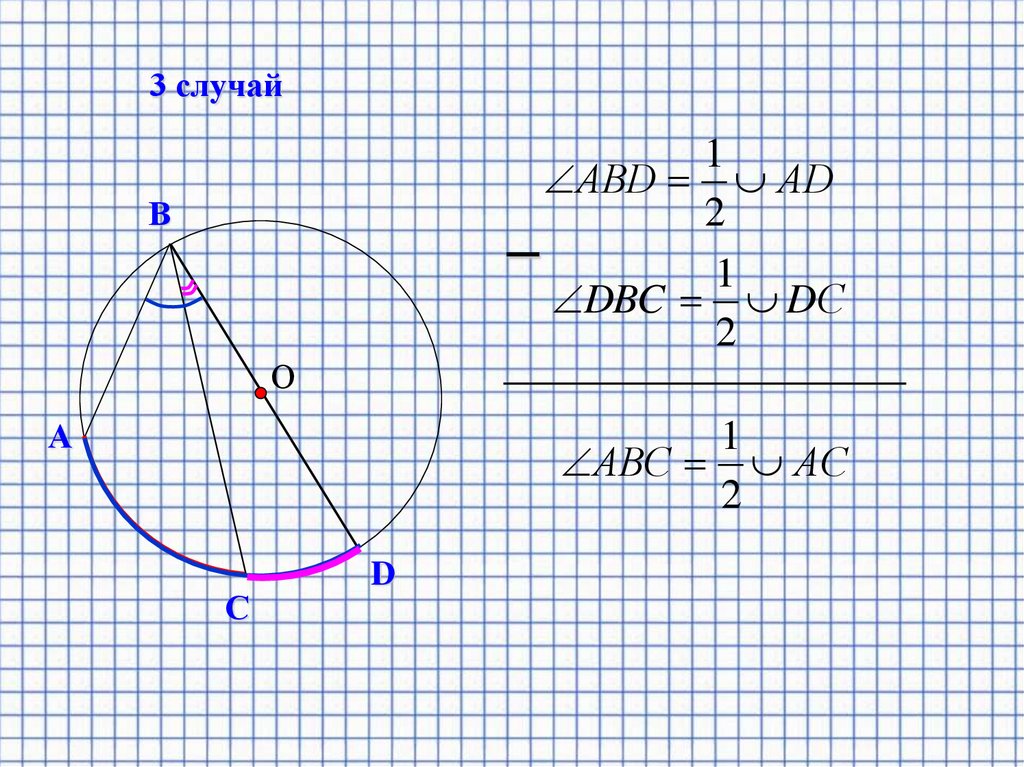
15.
3 случай1
АВD АD
2
–
1
DBC DС
2
В
О
А
1
АВС АС
2
С
D
16.
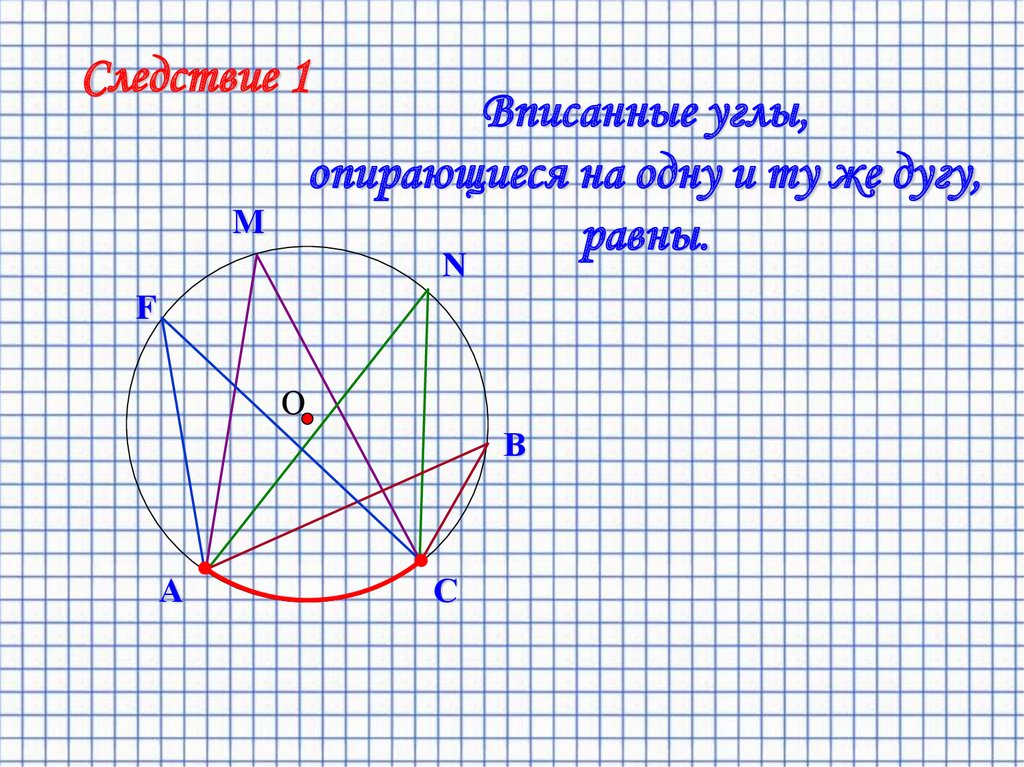
Следствие 1Вписанные углы,
опирающиеся на одну и ту же дугу,
равны.
M
N
F
О
В
А
С
17.
Следствие 2M
Вписанный угол,
опирающийся на
полуокружность – прямой.
N
F
О
А
С
В
18.
Домашнее задание§ 2стр 167 п.72,73 выучить
№ 649, 650














 mathematics
mathematics








