Similar presentations:
Центральные и вписанные углы
1.
Автор:Сидорова А.В.
МБОУ СОШ № 31
г. Мурманска
2. Дуга окружности
MО
В
А
АВ
АLB
АMВ
L
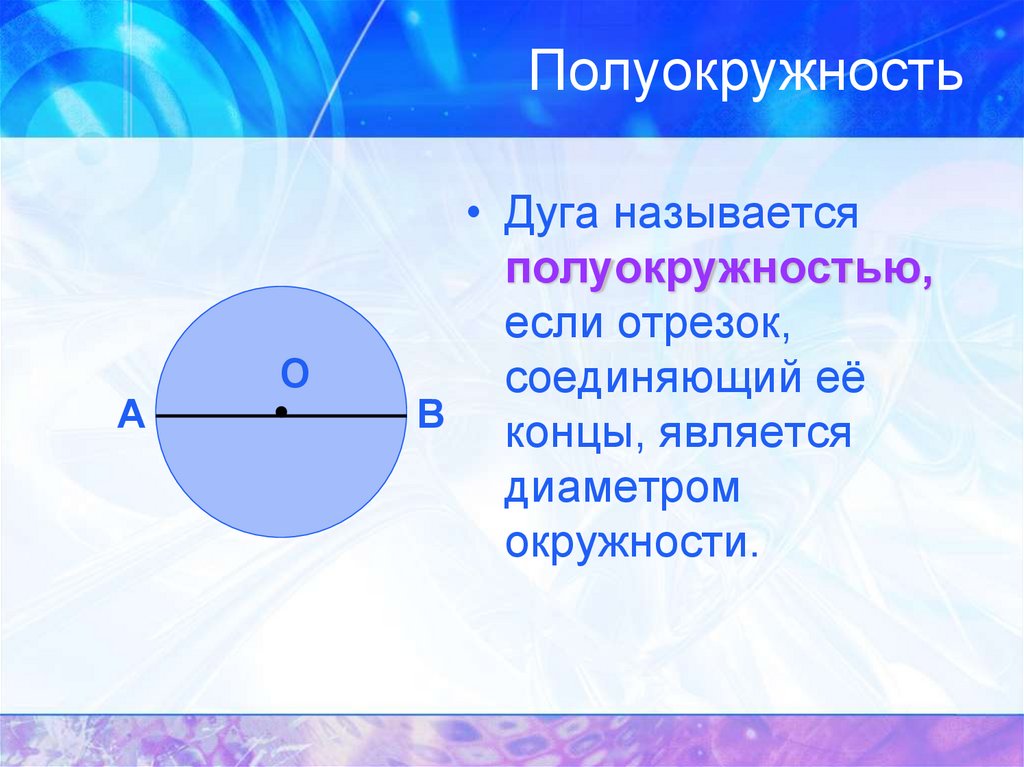
3. Полуокружность
АО
• Дуга называется
полуокружностью,
если отрезок,
соединяющий её
В концы, является
диаметром
окружности.
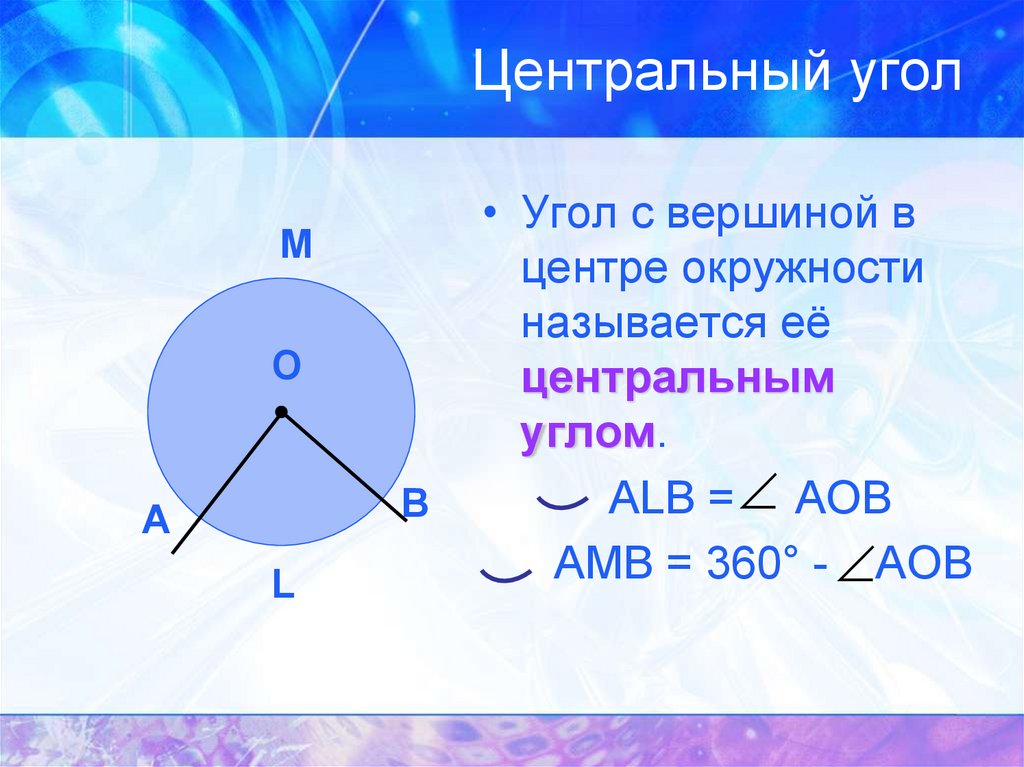
4. Центральный угол
MО
В
А
L
• Угол с вершиной в
центре окружности
называется её
центральным
углом.
ALB = AOB
AMB = 360° - AOB
5. Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной
градусноймере центрального угла АОВ.
6. Если дуга АВ окружности с центром О больше полуокружности, то её градусная мера считается равной 360° - АОВ.
Если дуга АВ окружности сцентром О больше
полуокружности, то её
градусная мера считается
равной 360° АОВ.
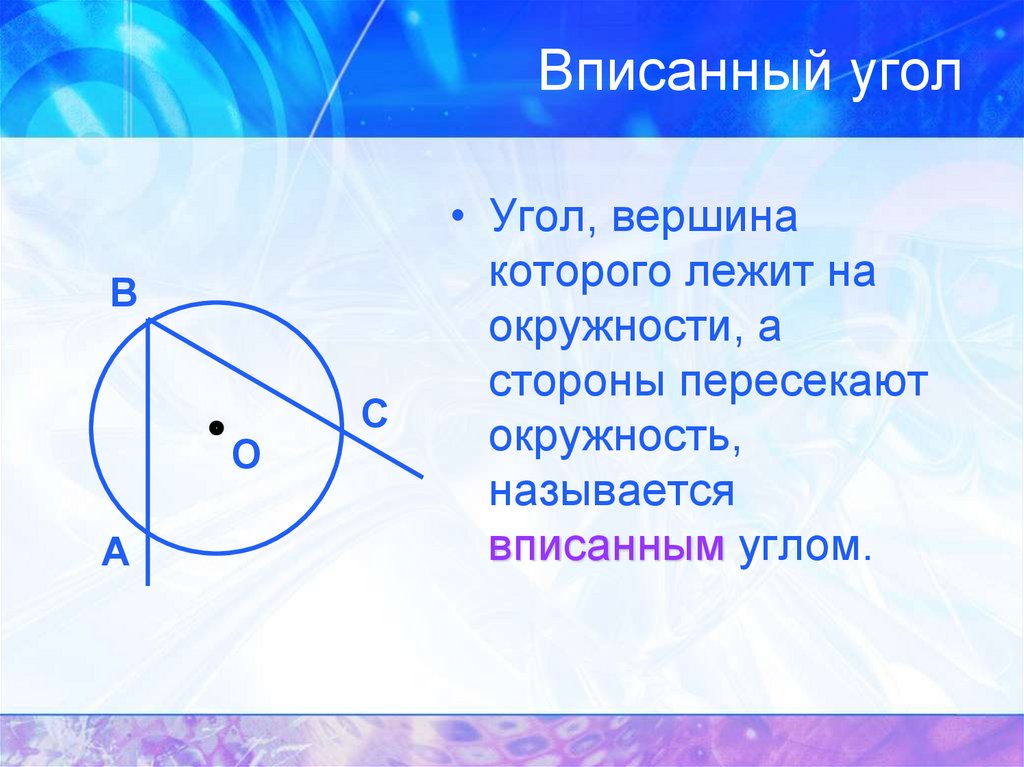
7. Вписанный угол
ВО
А
С
• Угол, вершина
которого лежит на
окружности, а
стороны пересекают
окружность,
называется
вписанным углом.
8. Теорема о вписанном угле
• Вписанный угол измеряется половинойдуги, на которую он опирается.
А
Дано: АВС – вписанный угол
1
Доказать: АВС = АС
2
Доказательство:
С
В
О
1) Луч ВО совпадает с одной из
сторон угла АВС
АОВ – равнобедренный, т. к. ОВ = ОА = r В = А
СОА – внешний угол СОА = ОВА + ОАВ
ОВА = ½ СОА
СОА = 2 ОВА
СВА = ½ АС.
9. 2 случай
АВС = АВD + DВСАВО = ½ АD
В
С
О
А
ОВС = ½ DС
АВС = ½ АD + ½ DС
D
АВС = ½ АС
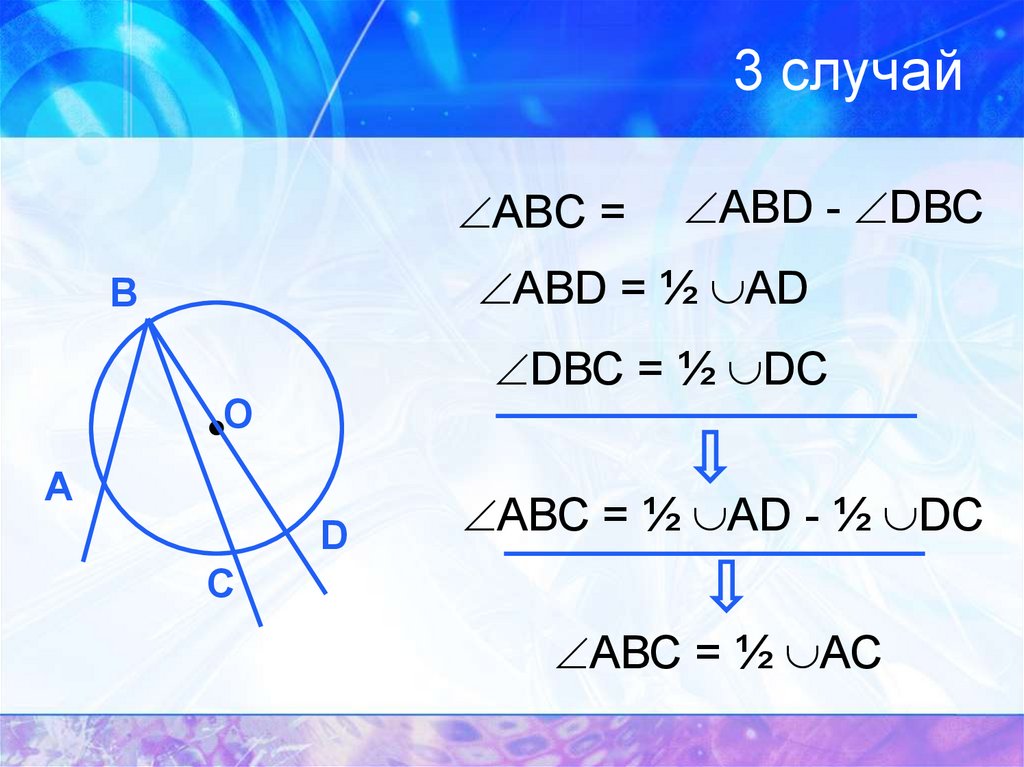
10. 3 случай
АВС =АВD - DВС
АВD = ½ АD
В
DВС = ½ DС
О
А
D
АВС = ½ АD - ½ DС
С
АВС = ½ АС
11. Следствие 1
• Вписанные углы,опирающиеся на
одну
и ту же дугу,
равны.
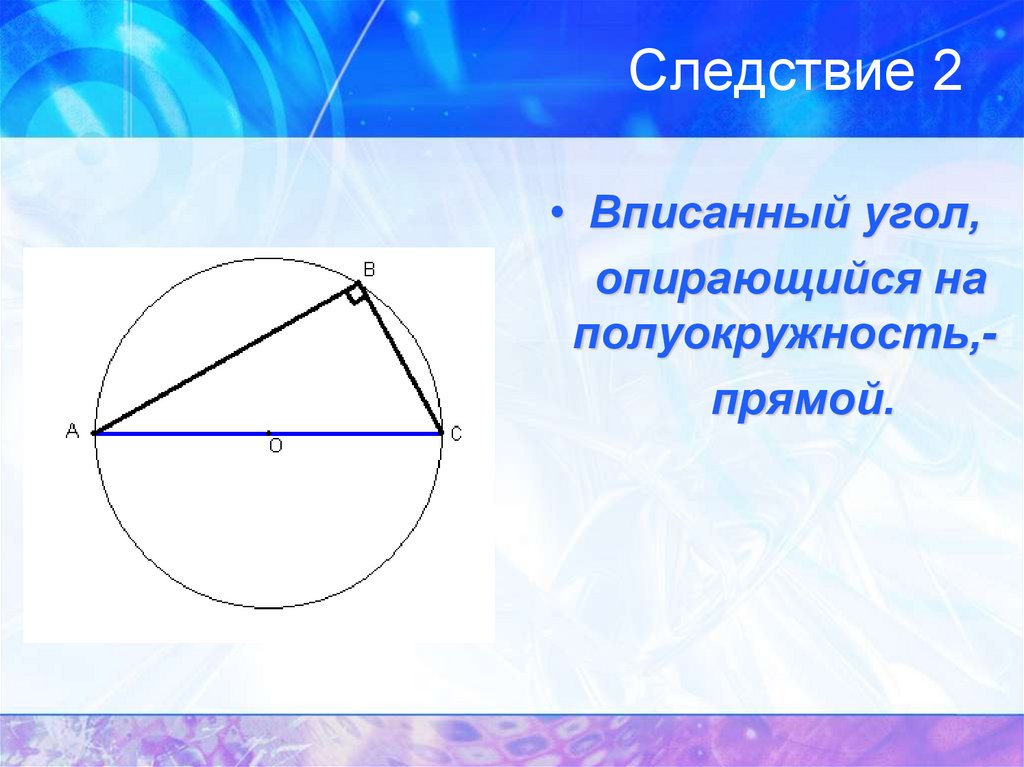
12. Следствие 2
• Вписанный угол,опирающийся на
полуокружность,прямой.
13.
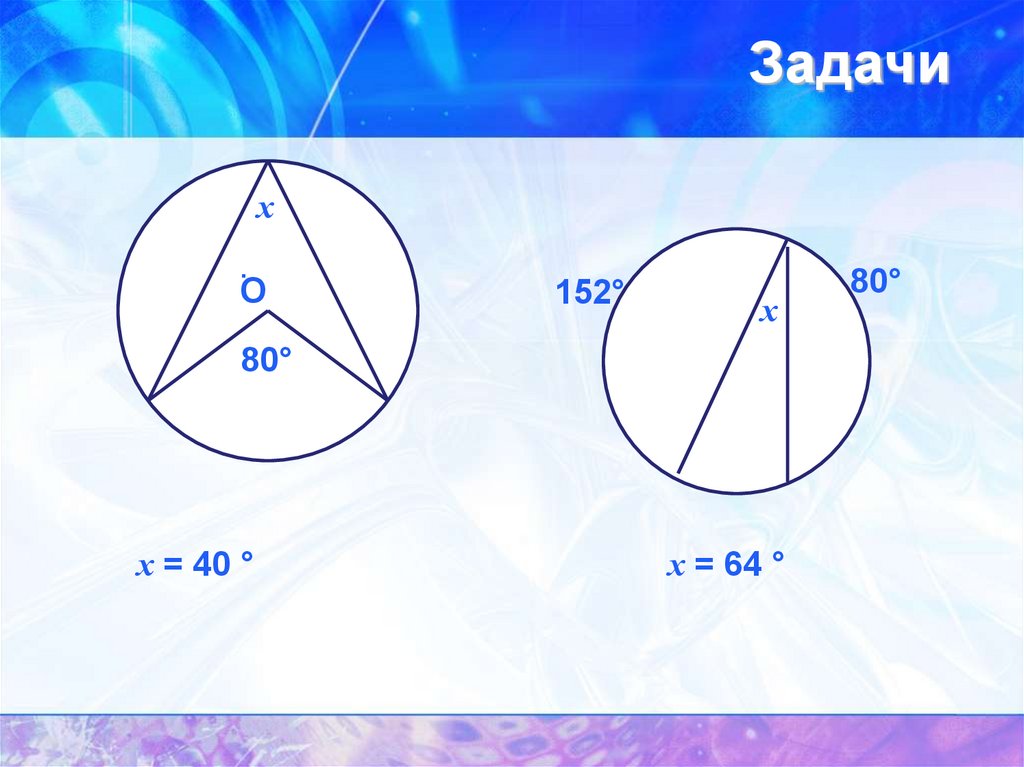
Задачих
.
О
152°
х
80°
х = 40 °
х = 64 °
80°
14.
Задачих
20°
215°
80°
х
.
О
х = 105 °
х = 50 °








 mathematics
mathematics