Similar presentations:
Центральные и вписанные углы
1.
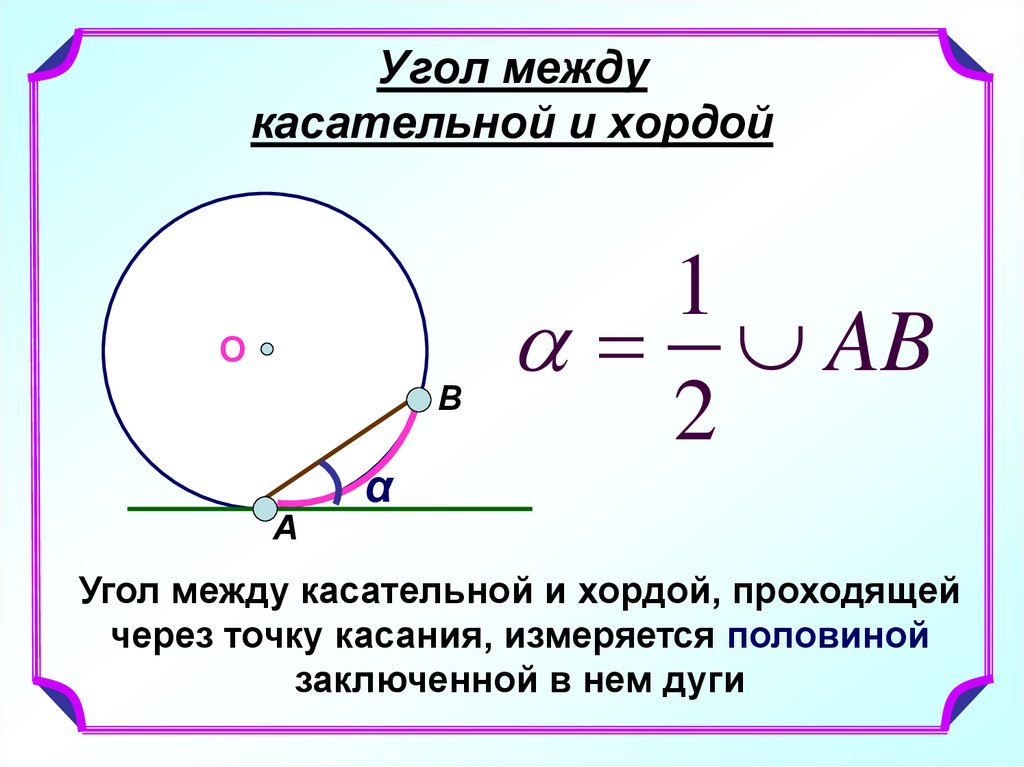
2. Угол между касательной и хордой
ОВ
А
1
AB
2
α
Угол между касательной и хордой, проходящей
через точку касания, измеряется половиной
заключенной в нем дуги
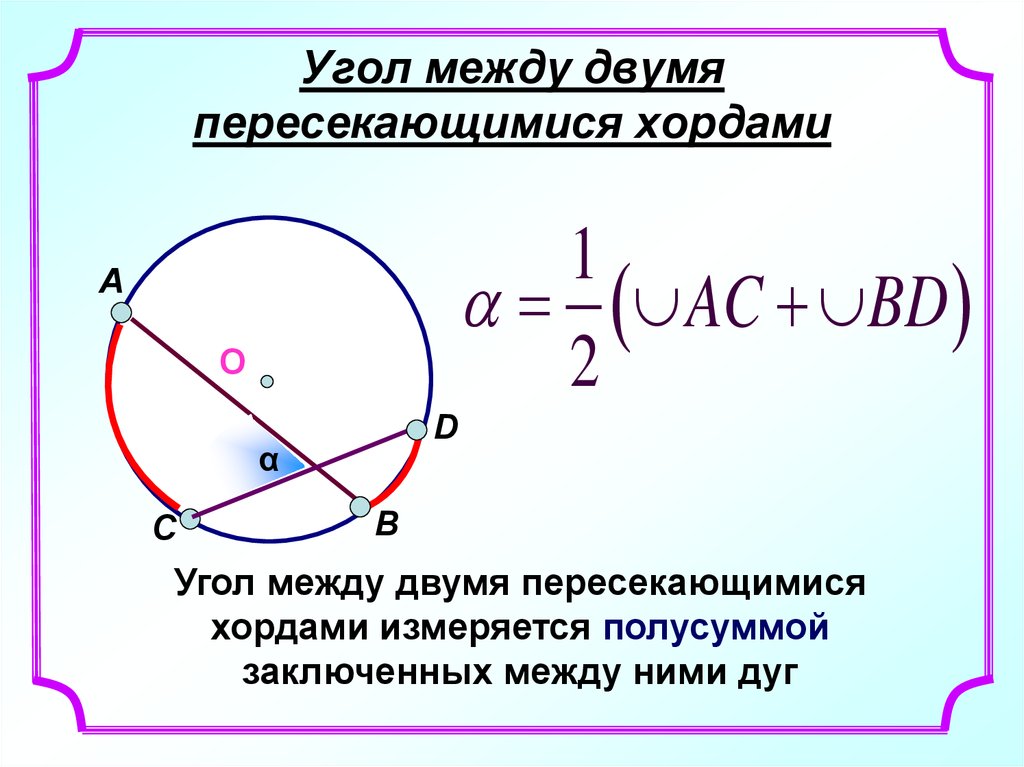
3. Угол между двумя пересекающимися хордами
1AC BD
2
А
О
D
α
С
В
Угол между двумя пересекающимися
хордами измеряется полусуммой
заключенных между ними дуг
4. Угол между двумя секущими, проведенными из одной точки
1CE BD
2
C
B
О
α
E
D
А
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
5. Угол между касательной и секущей, проведенными из одной точки
BО
D
C
1
BD BC
2
α
A
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
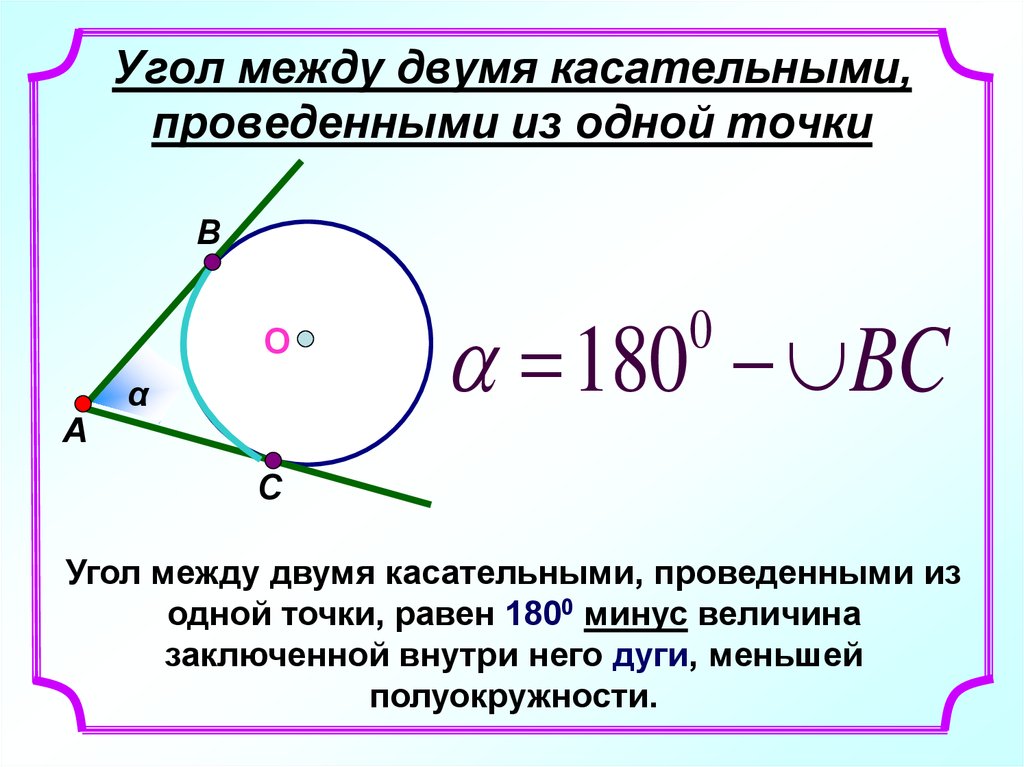
6. Угол между двумя касательными, проведенными из одной точки
BО
α
180 BC
0
A
C
Угол между двумя касательными, проведенными из
одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.
7.
Дуга окружностиАВ
А
М
N
АМВ
АNВ
О
В
8.
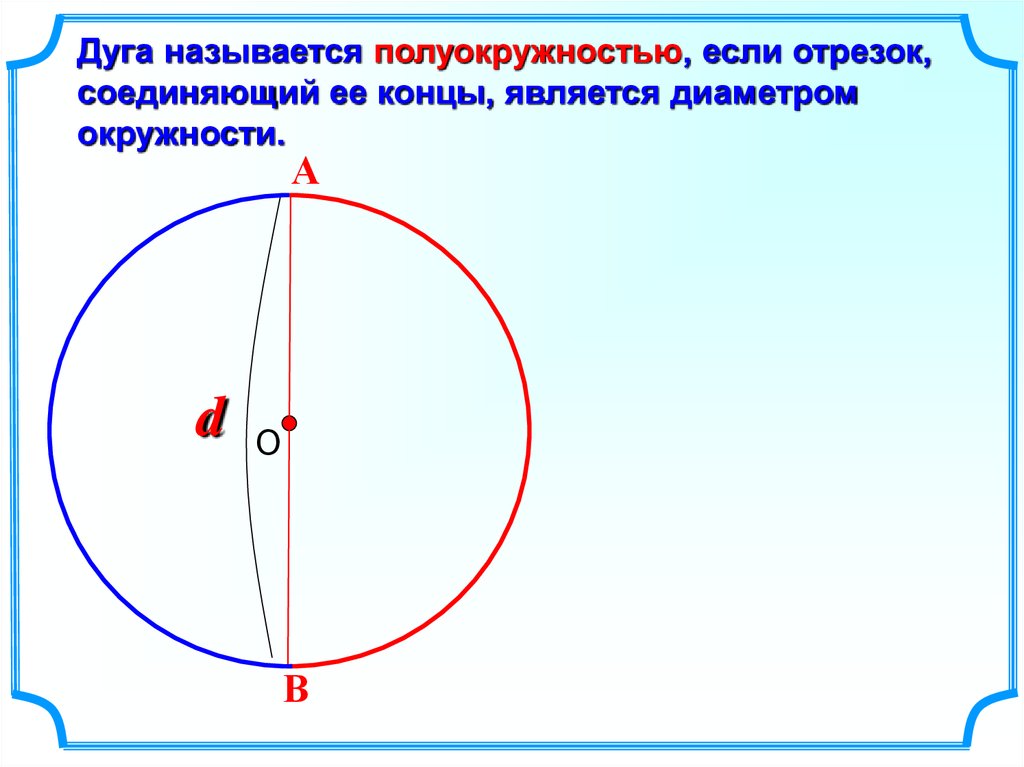
Дуга называется полуокружностью, если отрезок,соединяющий ее концы, является диаметром
окружности.
А
d
О
В
9.
АО
В
АВ АОВ 180
0
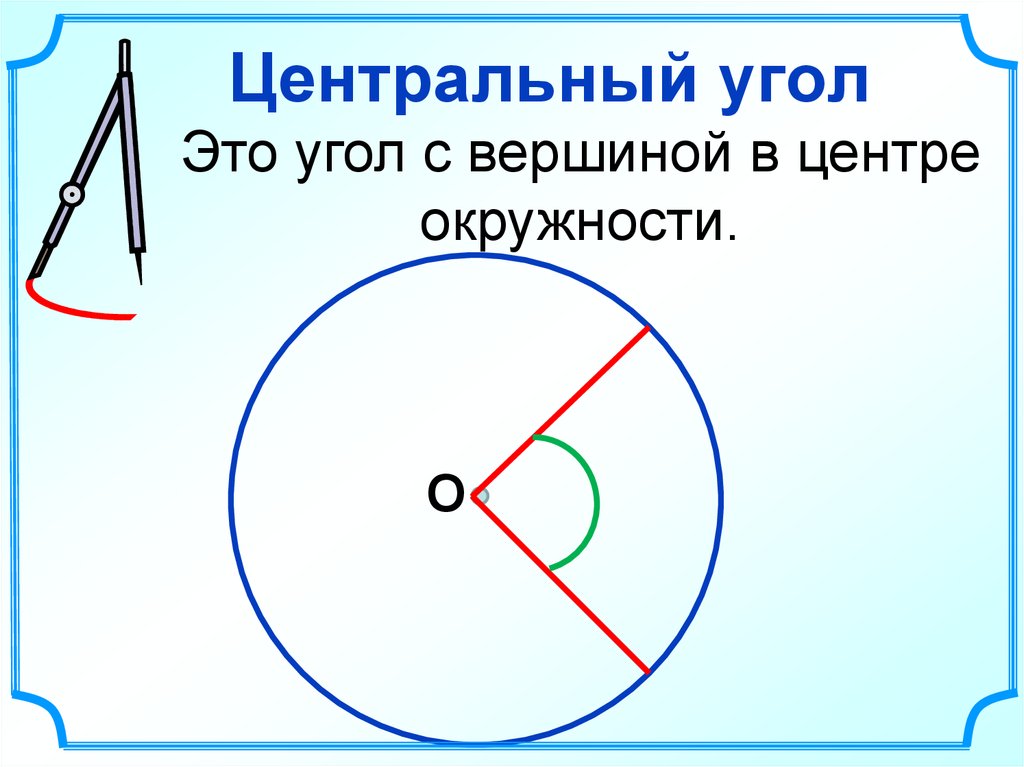
10. Центральный угол
Это угол с вершиной в центреокружности.
О
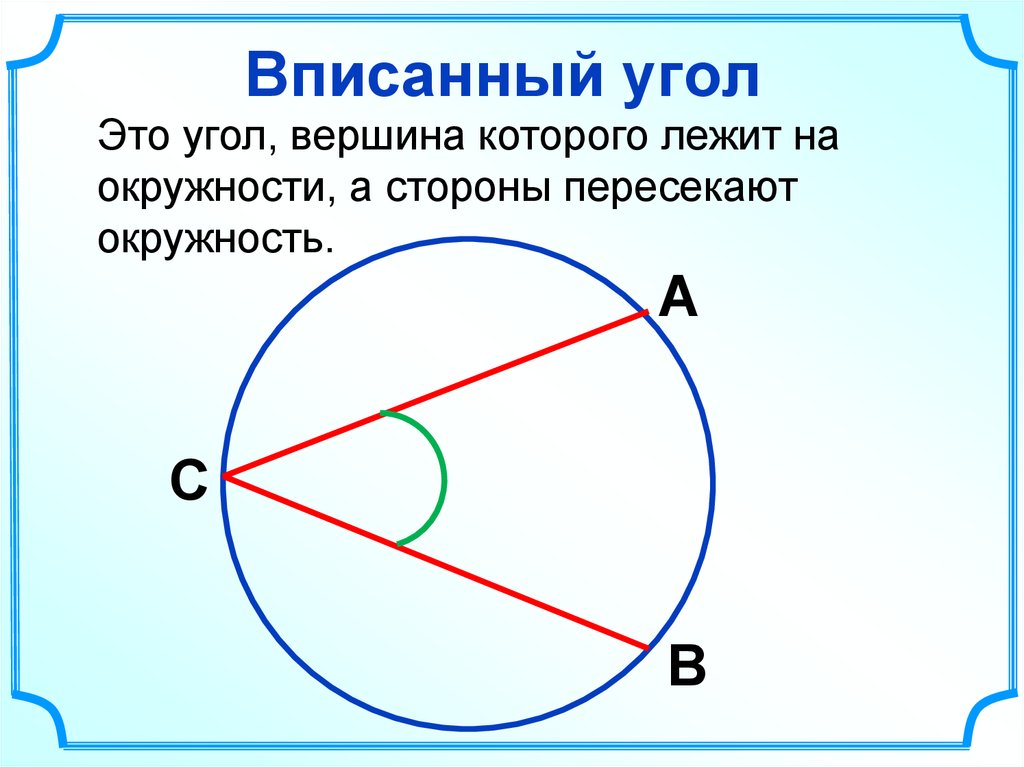
11. Вписанный угол
Это угол, вершина которого лежит наокружности, а стороны пересекают
окружность.
А
С
В
12.
Следствие 1Вписанные углы,
опирающиеся на одну и ту же дугу, равны.
M
N
F
О
В
А
С
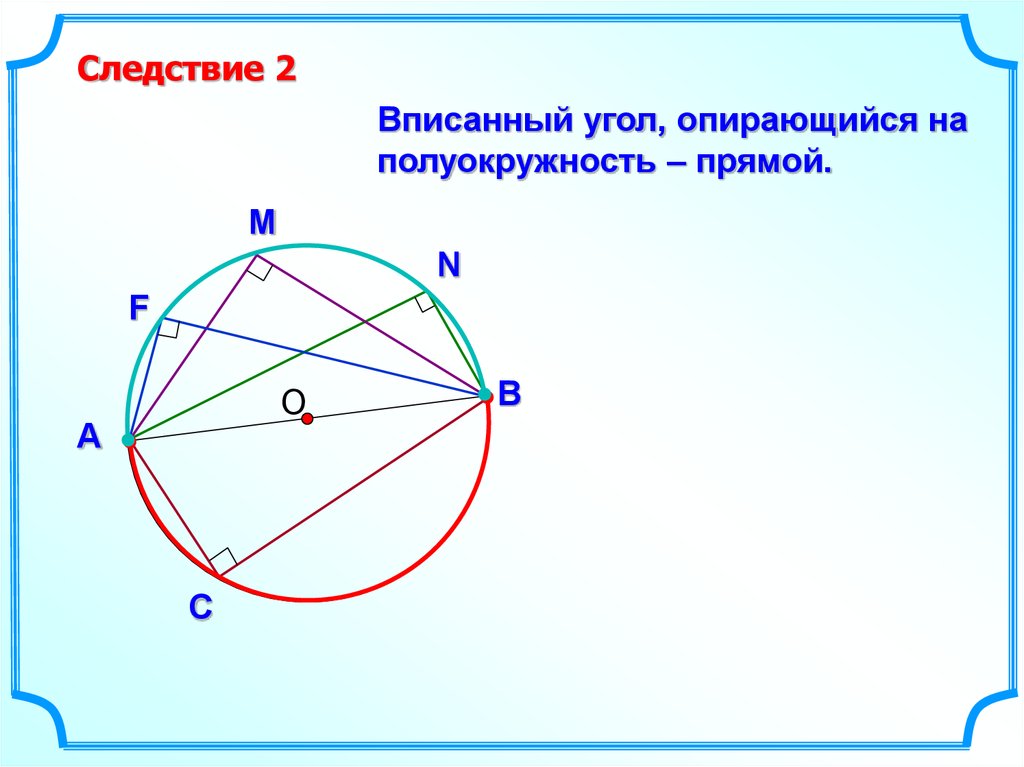
13.
Следствие 2Вписанный угол, опирающийся на
полуокружность – прямой.
M
N
F
О
А
С
В
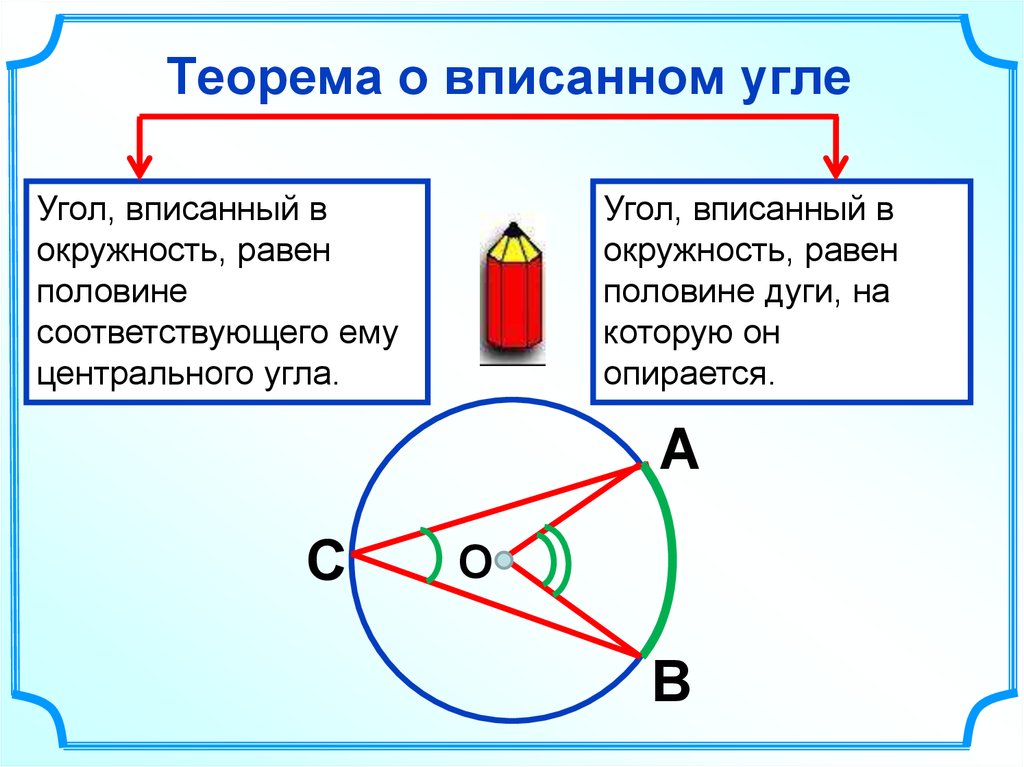
14. Теорема о вписанном угле
Угол, вписанный вокружность, равен
половине
соответствующего ему
центрального угла.
Угол, вписанный в
окружность, равен
половине дуги, на
которую он
опирается.
А
С
О
В
15.
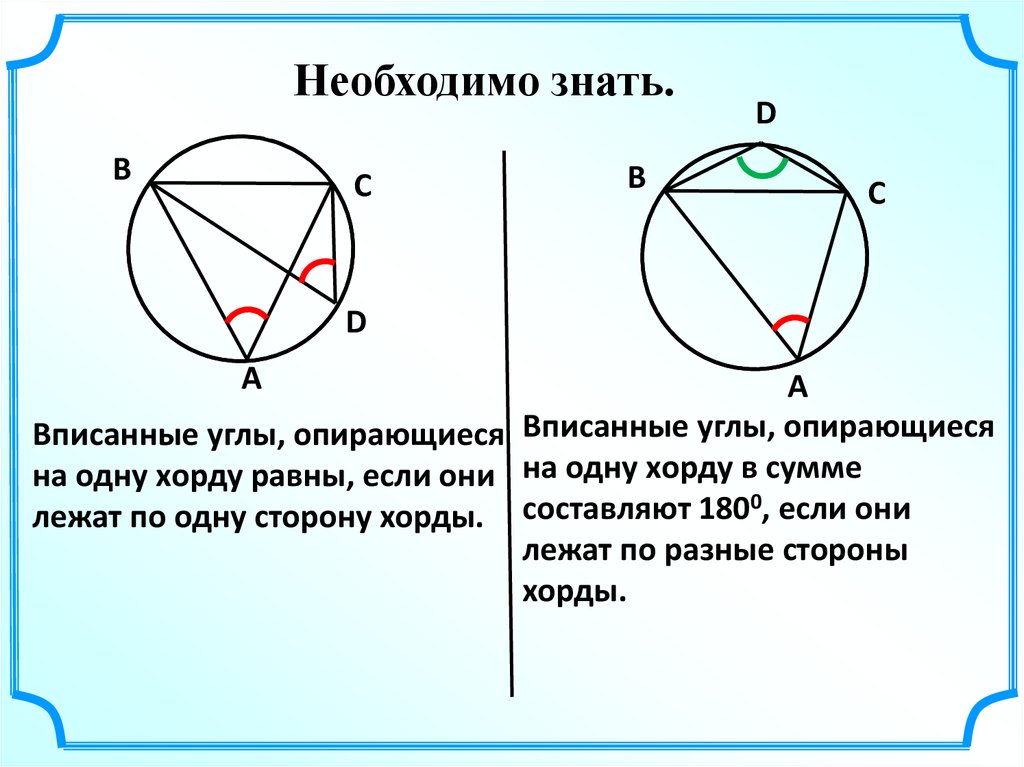
Необходимо знать.В
С
В
D
С
D
А
А
Вписанные углы, опирающиеся Вписанные углы, опирающиеся
на одну хорду равны, если они на одну хорду в сумме
0
лежат по одну сторону хорды. составляют 180 , если они
лежат по разные стороны
хорды.
16.
Тренажер17.
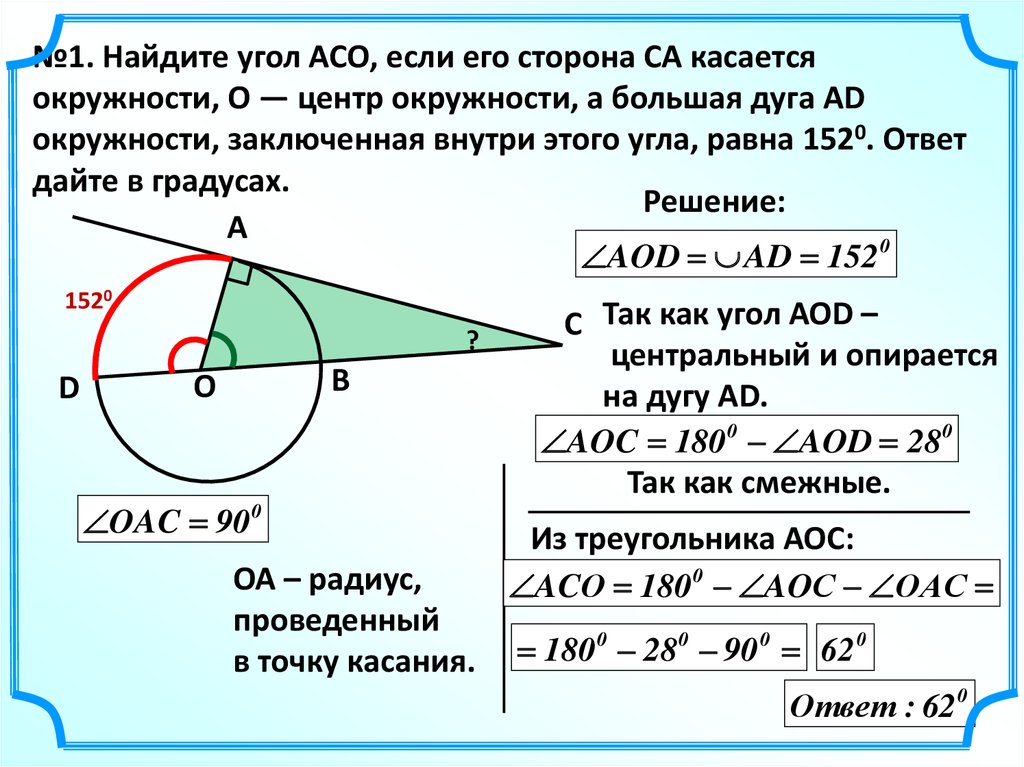
№1. Найдите угол ACO, если его сторона CA касаетсяокружности, O — центр окружности, а большая дуга AD
окружности, заключенная внутри этого угла, равна 1520. Ответ
дайте в градусах.
Решение:
А
AOD AD 152 0
1520
?
D
В
О
OAC 90 0
ОА – радиус,
проведенный
в точку касания.
C Так как угол АОD –
центральный и опирается
на дугу AD.
AOC 180 0 AOD 28 0
Так как смежные.
Из треугольника АОС:
ACО 180 0 AOС ОАС
180 0 28 0 90 0 62 0
Ответ : 62170
18.
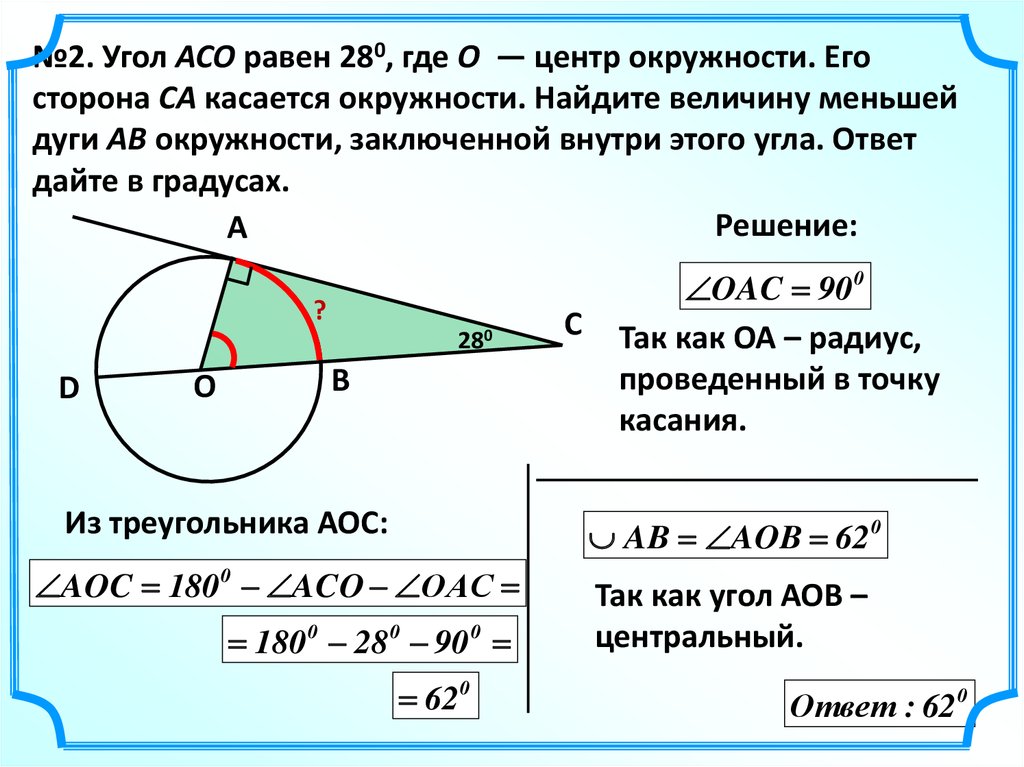
№2. Угол ACO равен 280, где O — центр окружности. Егосторона CA касается окружности. Найдите величину меньшей
дуги AB окружности, заключенной внутри этого угла. Ответ
дайте в градусах.
Решение:
А
?
280
D
О
В
Из треугольника АОС:
C
OAC 90 0
Так как ОА – радиус,
проведенный в точку
касания.
AB AOB 62 0
AOC 180 0 ACO ОАС
180 0 28 0 90 0
62 0
Так как угол АОВ –
центральный.
Ответ : 62180
19.
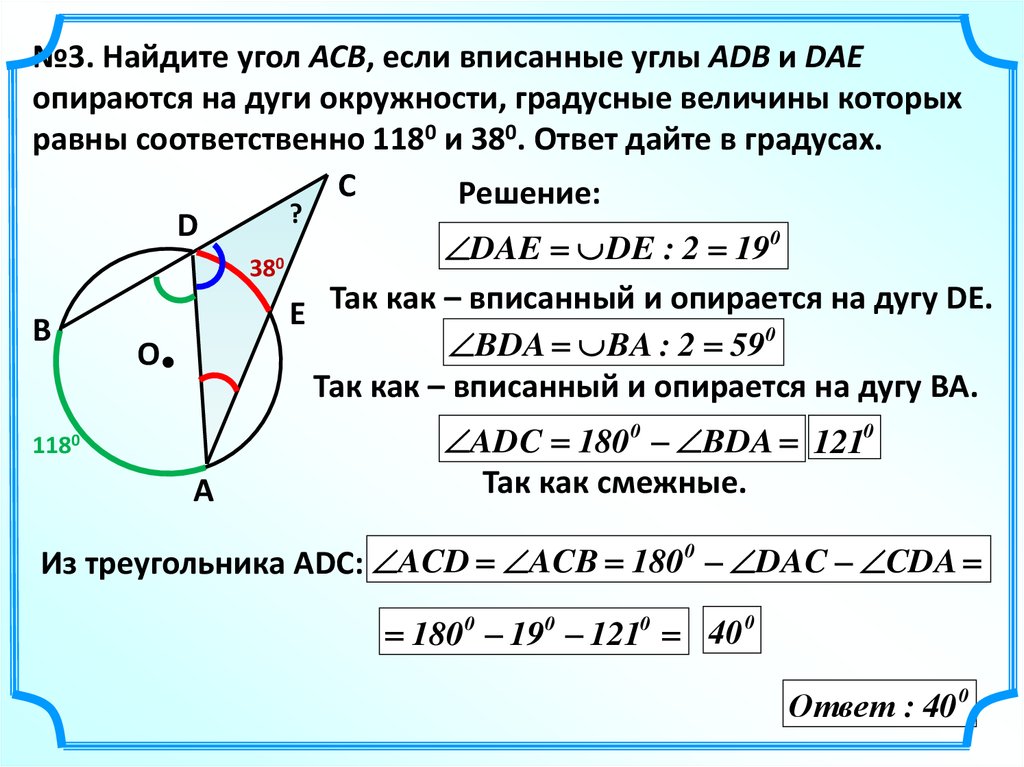
№3. Найдите угол ACB, если вписанные углы ADB и DAEопираются на дуги окружности, градусные величины которых
равны соответственно 1180 и 380. Ответ дайте в градусах.
C
Решение:
?
D
0
DAE
DE
:
2
19
380
Так как – вписанный и опирается на дугу DE.
E
B
0
BDA
BA
:
2
59
O
Так как – вписанный и опирается на дугу BA.
1180
A
ADC 180 0 BDA 1210
Так как смежные.
Из треугольника АDС: ACD ACB 180 0 DAC CDA
180 0 190 1210 40 0
Ответ : 40190
20.
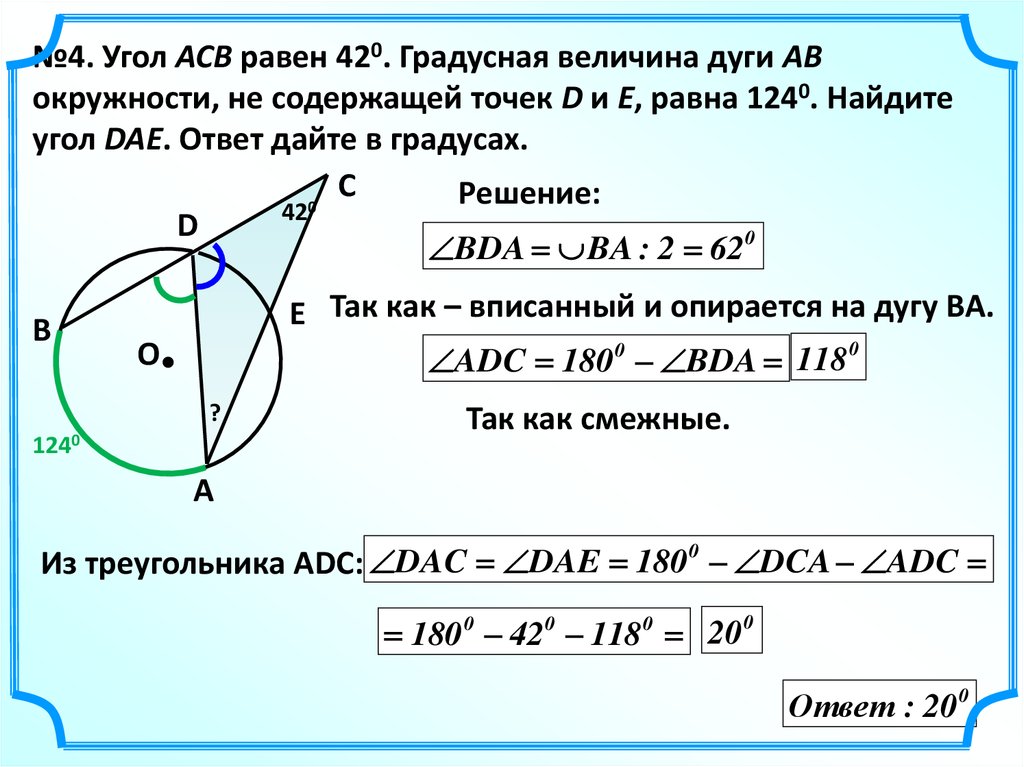
№4. Угол ACB равен 420. Градусная величина дуги ABокружности, не содержащей точек D и E, равна 1240. Найдите
угол DAE. Ответ дайте в градусах.
C
Решение:
0
42
D
BDA BA : 2 62 0
B
E Так как – вписанный и опирается на дугу BA.
ADC 180 0 BDA 118 0
O
?
1240
Так как смежные.
A
Из треугольника АDС: DAC DAE 180 0 DCA ADC
180 0 42 0 118 0 20 0
Ответ : 20200
21.
№5. Чему равен острый вписанный угол, опирающийся нахорду, равную радиусу окружности? Ответ дайте в градусах.
A
?
O
C
Решение:
Рассмотрим треугольник ОСВ.
ОС=ОВ так как радиусы одной окружности.
ВС=ОС=ОВ по условию.
B
=> Треугольник ОСВ – равносторонний.
=> Угол СОВ=600 => Величина дуги ВС=600.
Так как угол СОВ – центральный и опирается на дугу BС.
CAB BC : 2 30 0
Так как – вписанный и опирается на дугу BС.
Ответ : 30210
22.
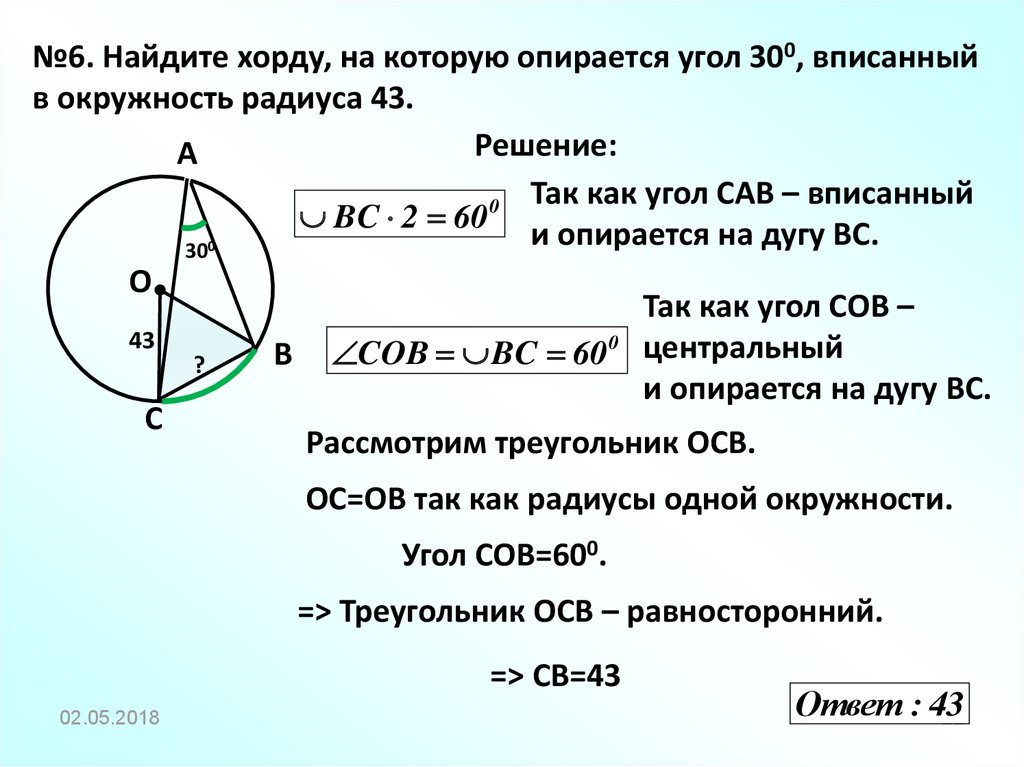
№6. Найдите хорду, на которую опирается угол 300, вписанныйв окружность радиуса 43.
Решение:
A
Так как угол СAВ – вписанный
0
BC 2 60
и опирается на дугу BС.
300
O
Так как угол СОВ –
43
0 центральный
COB
BC
60
B
?
и опирается на дугу BС.
C
Рассмотрим треугольник ОСВ.
ОС=ОВ так как радиусы одной окружности.
Угол СОВ=600.
=> Треугольник ОСВ – равносторонний.
=> СВ=43
02.05.2018
Ответ : 43
22
23.
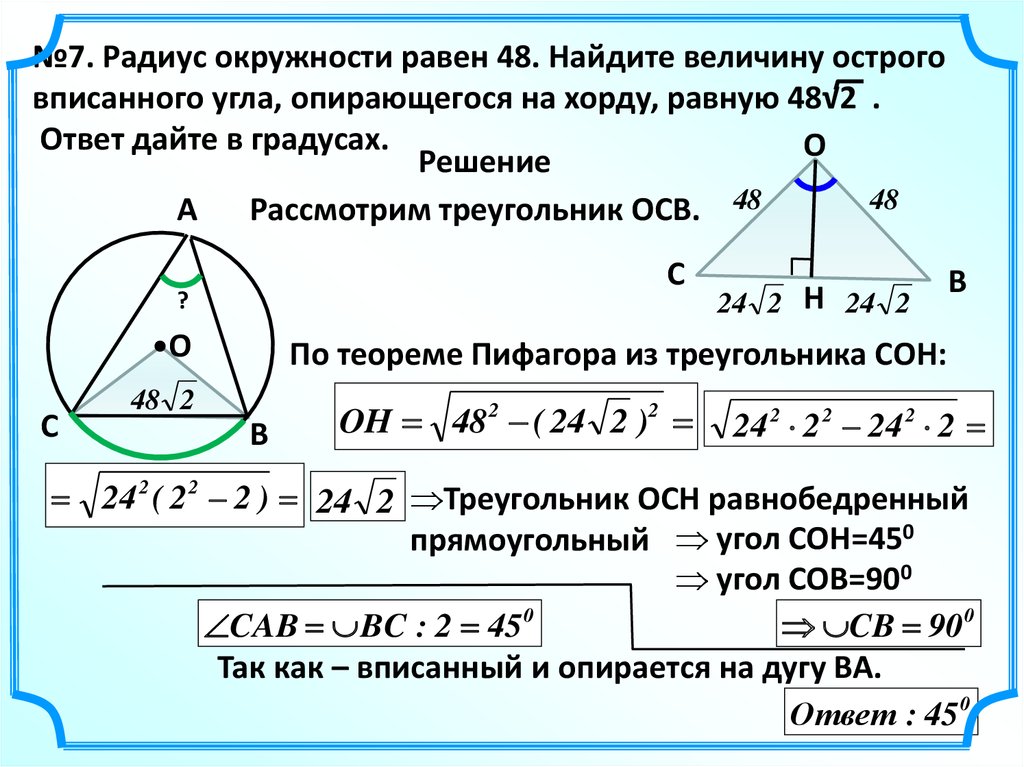
№7. Радиус окружности равен 48. Найдите величину остроговписанного угла, опирающегося на хорду, равную 48√2 .
Ответ дайте в градусах.
O
Решение
A
Рассмотрим треугольник ОСВ. 48
C
?
O
C
48
24 2 H 24 2
B
По теореме Пифагора из треугольника СОН:
48 2
B
OH 48 2 ( 24 2 )2
24 2 2 2 24 2 2
24 2 ( 2 2 2 ) 24 2 Треугольник ОСН равнобедренный
прямоугольный угол СОН=450
угол СОВ=900
CAB BC : 2 45 0
CB 90 0
Так как – вписанный и опирается на дугу BA.
Ответ : 45230
24.
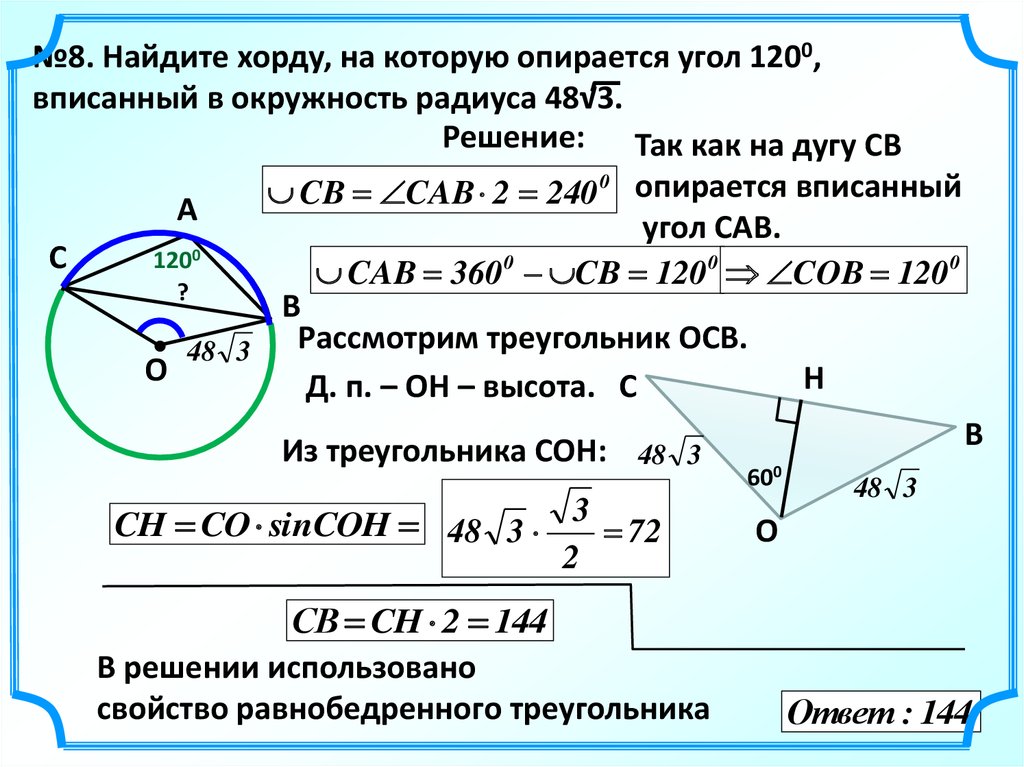
№8. Найдите хорду, на которую опирается угол 1200,вписанный в окружность радиуса 48√3.
Решение: Так как на дугу СВ
0 опирается вписанный
CB
CAB
2
240
A
угол САВ.
0
120
C
0
0
0
CAB
360
CB
120
COB
120
?
B
Рассмотрим треугольник ОСВ.
48 3
O
H
Д. п. – ОН – высота. C
Из треугольника СОН: 48 3
CH CO sinCOH 48 3 3 72
2
СB CH 2 144
В решении использовано
свойство равнобедренного треугольника
B
600
48 3
O
Ответ : 144
24
25.
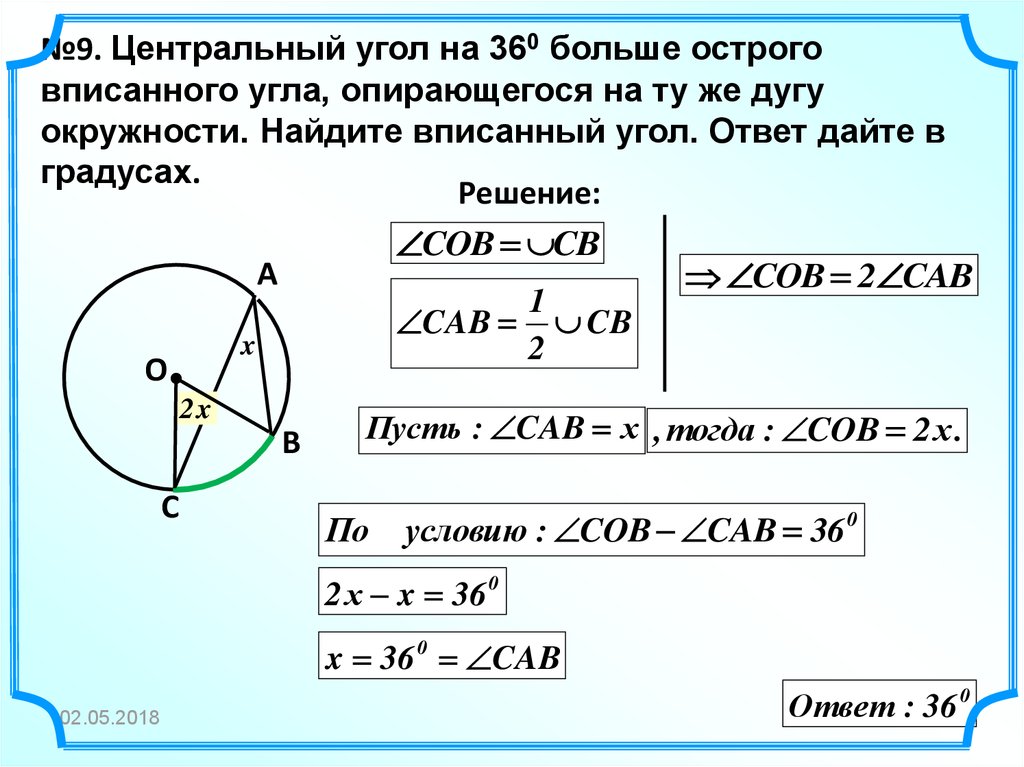
№9. Центральный угол на 360 больше остроговписанного угла, опирающегося на ту же дугу
окружности. Найдите вписанный угол. Ответ дайте в
градусах.
Решение:
COB CB
A
COB 2 CAB
1
CAB CB
x
2
O
2x
B
C
Пусть : CAB х , тогда : COB 2 х .
По
условию : COB CAB 36 0
2 х x 36 0
x 36 0 CAB
02.05.2018
Ответ : 36250
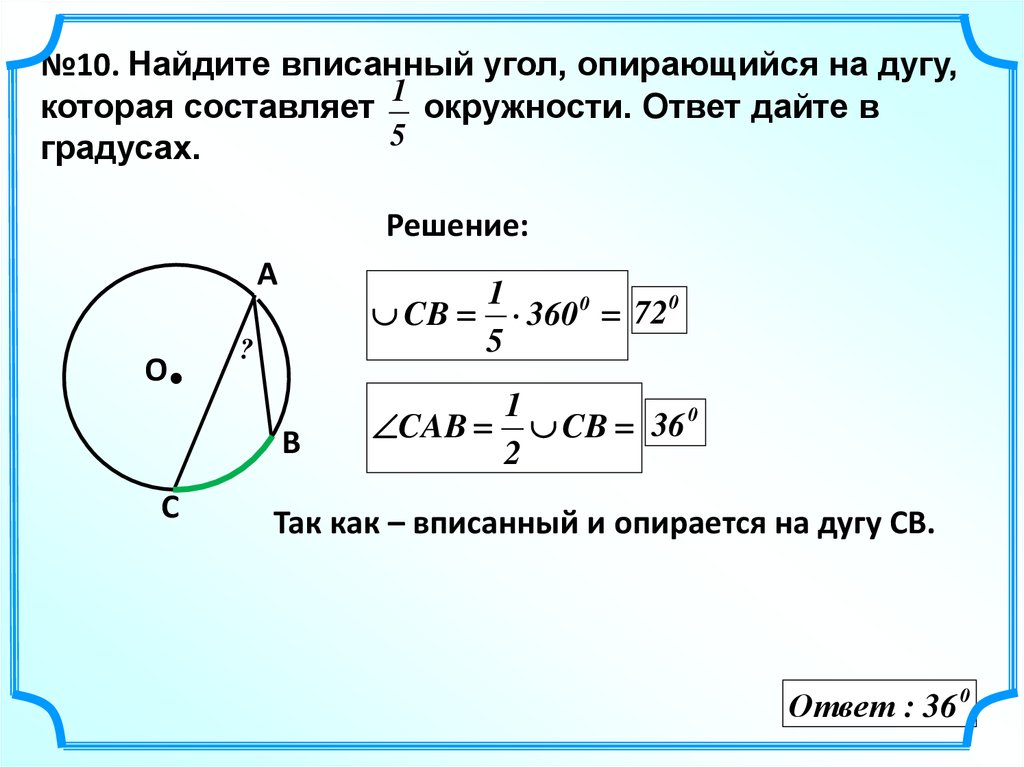
26.
№10. Найдите вписанный угол, опирающийся на дугу,которая составляет 1 окружности. Ответ дайте в
5
градусах.
Решение:
A
O
1
CB 360 0 720
5
?
B
C
CAB
1
CB 36 0
2
Так как – вписанный и опирается на дугу СВ.
Ответ : 36260
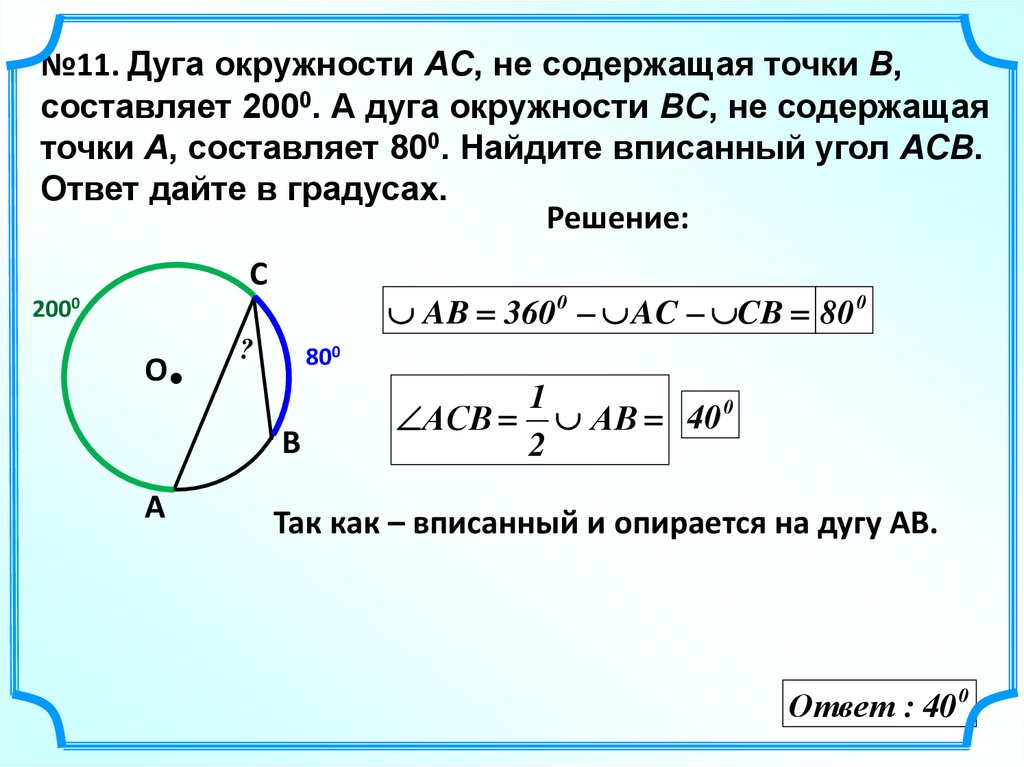
27.
№11. Дуга окружности AC, не содержащая точки B,составляет 2000. А дуга окружности BC, не содержащая
точки A, составляет 800. Найдите вписанный угол ACB.
Ответ дайте в градусах.
Решение:
C
AB 360 0 AC CB 80 0
2000
O
?
800
B
A
1
АСB АB 40 0
2
Так как – вписанный и опирается на дугу АВ.
Ответ : 40270
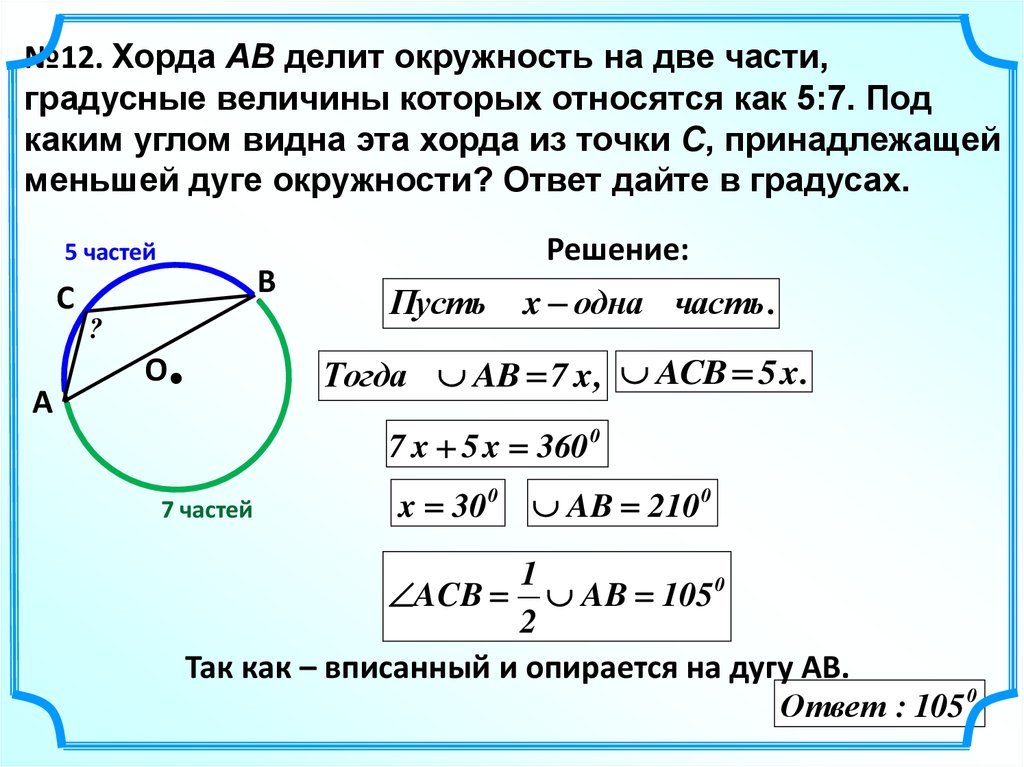
28.
№12. Хорда AB делит окружность на две части,градусные величины которых относятся как 5:7. Под
каким углом видна эта хорда из точки C, принадлежащей
меньшей дуге окружности? Ответ дайте в градусах.
Решение:
5 частей
B
C
?
A
Пусть
x одна часть .
Тогда AB 7 x , ACB 5 x .
O
7 x 5 x 360 0
7 частей
x 30 0
AB 210 0
1
ACB AB 105 0
2
Так как – вписанный и опирается на дугу АВ.
0
Ответ : 105
28
29.
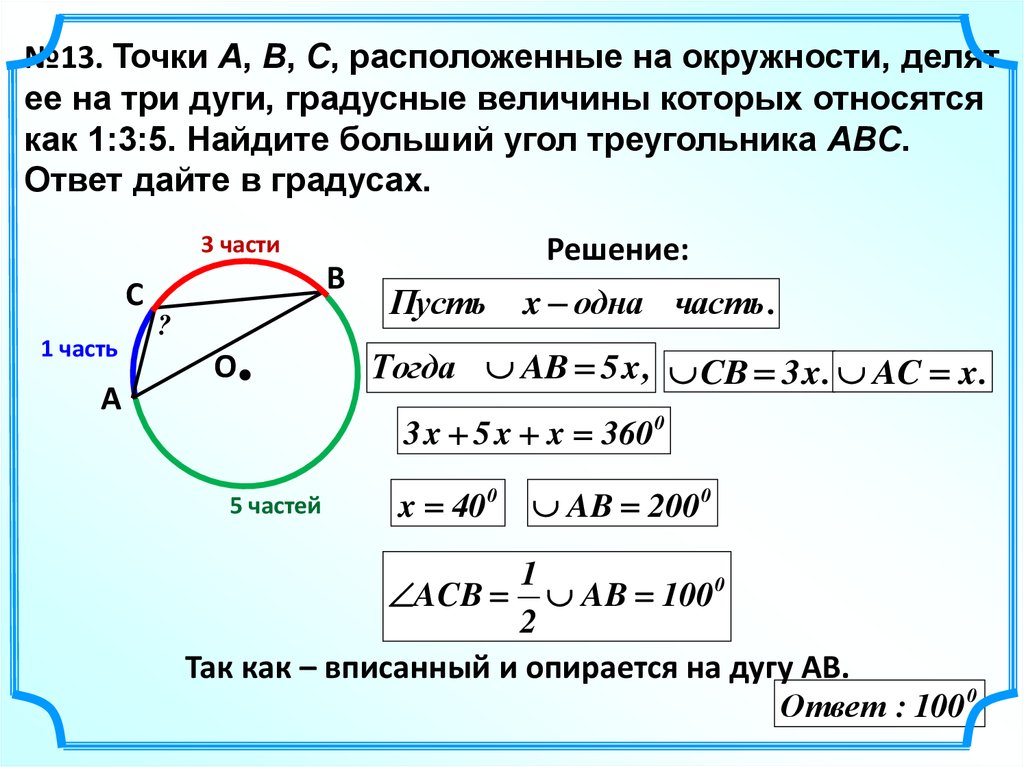
№13. Точки A, B, C, расположенные на окружности, делятее на три дуги, градусные величины которых относятся
как 1:3:5. Найдите больший угол треугольника ABC.
Ответ дайте в градусах.
3 части
B
C
1 часть
A
?
O
Решение:
Пусть
x одна часть .
Тогда AB 5 x , CB 3 x . AC x .
3 x 5 x x 360 0
5 частей
x 40 0
AB 200 0
1
ACB AB 100 0
2
Так как – вписанный и опирается на дугу АВ.
0
Ответ : 100
29
30.
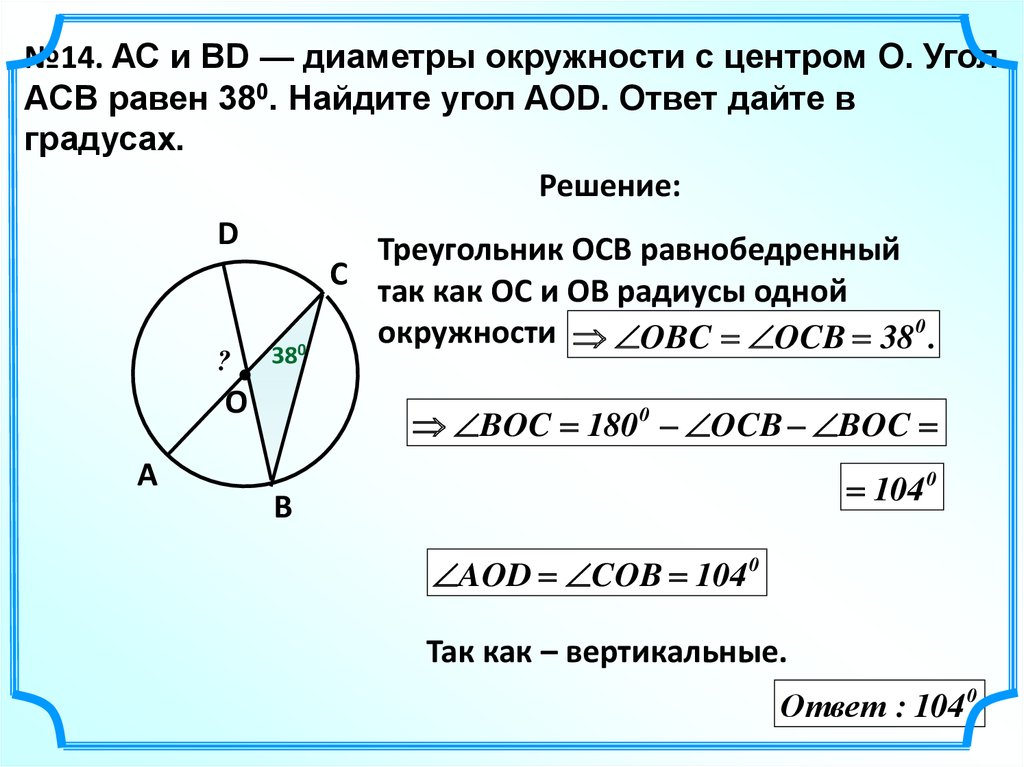
№14. АС и ВD — диаметры окружности с центром O. УголACB равен 380. Найдите угол AOD. Ответ дайте в
градусах.
Решение:
D
Треугольник ОСВ равнобедренный
C так как ОС и ОВ радиусы одной
?
380
O
A
окружности OBC OCB 38 0 .
BOC 180 0 OCB BOC
104 0
B
AOD COB 104 0
Так как – вертикальные.
0
Ответ : 104
30
31.
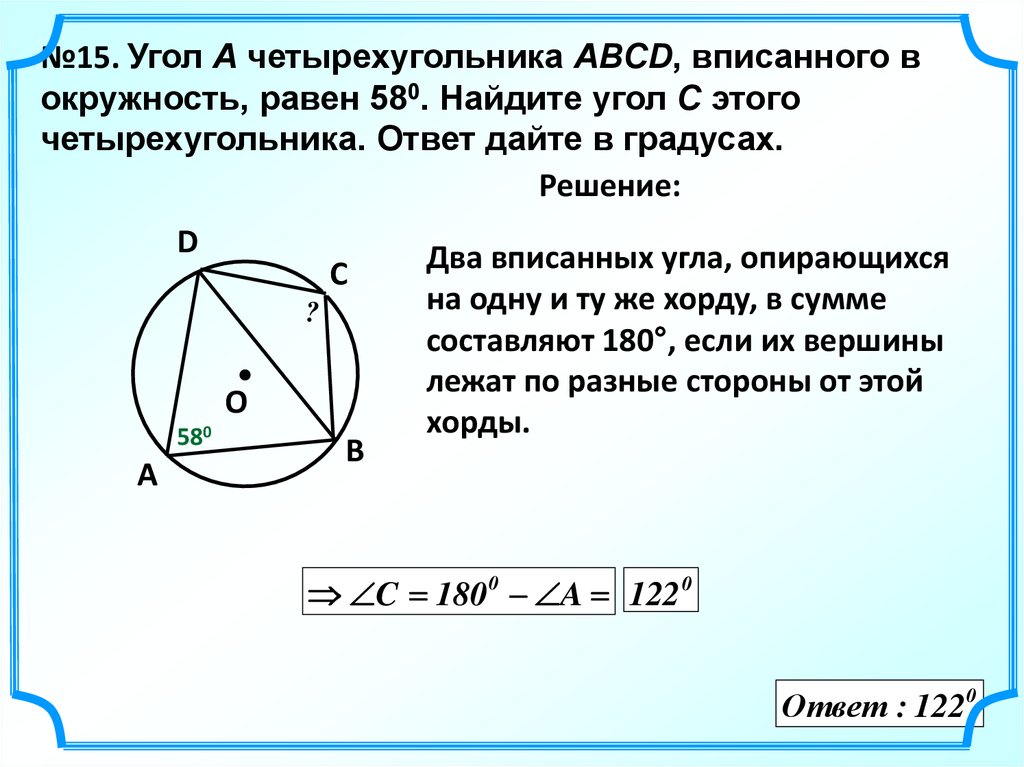
№15. Угол A четырехугольника ABCD, вписанного вокружность, равен 580. Найдите угол C этого
четырехугольника. Ответ дайте в градусах.
Решение:
D
C
?
O
580
A
B
Два вписанных угла, опирающихся
на одну и ту же хорду, в сумме
составляют 180°, если их вершины
лежат по разные стороны от этой
хорды.
C 180 0 A 122 0
0
Ответ : 122
31
32.
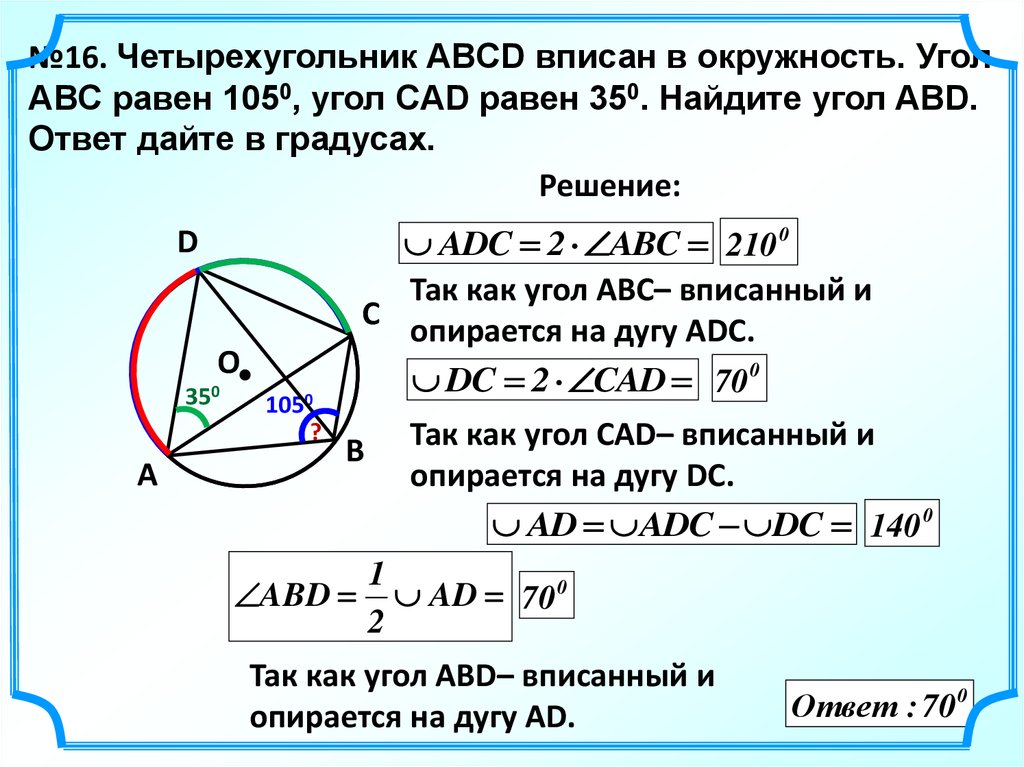
№16. Четырехугольник ABCD вписан в окружность. УголABC равен 1050, угол CAD равен 350. Найдите угол ABD.
Ответ дайте в градусах.
Решение:
D
O
350
A
1050
?
ADC 2 ABC 210 0
Так как угол ABC– вписанный и
C опирается на дугу АDC.
DC 2 CAD 70 0
B
Так как угол CAD– вписанный и
опирается на дугу DC.
AD ADC DC 140 0
1
ABD AD 70 0
2
Так как угол АBD– вписанный и
опирается на дугу AD.
Ответ : 70320
33.
№19. Через концы A, B дуги окружности в 620 проведеныкасательные AC и BC. Найдите угол ACB. Ответ дайте в
градусах.
Решение:
C
Так как угол АОВ –
?
AOB 92 0 центральный и
920
опирается на дугу АВ.
B
A
OBC OAC 90 0
O
Свойство радиуса, проведенного в точку
касания.
ACB 360 0 AOB OAC OBC
360 0 90 0 90 0 92 0 88 0
Так как сумма углов четырехугольника = 3600.
Ответ : 88330
34. Решение упражнений
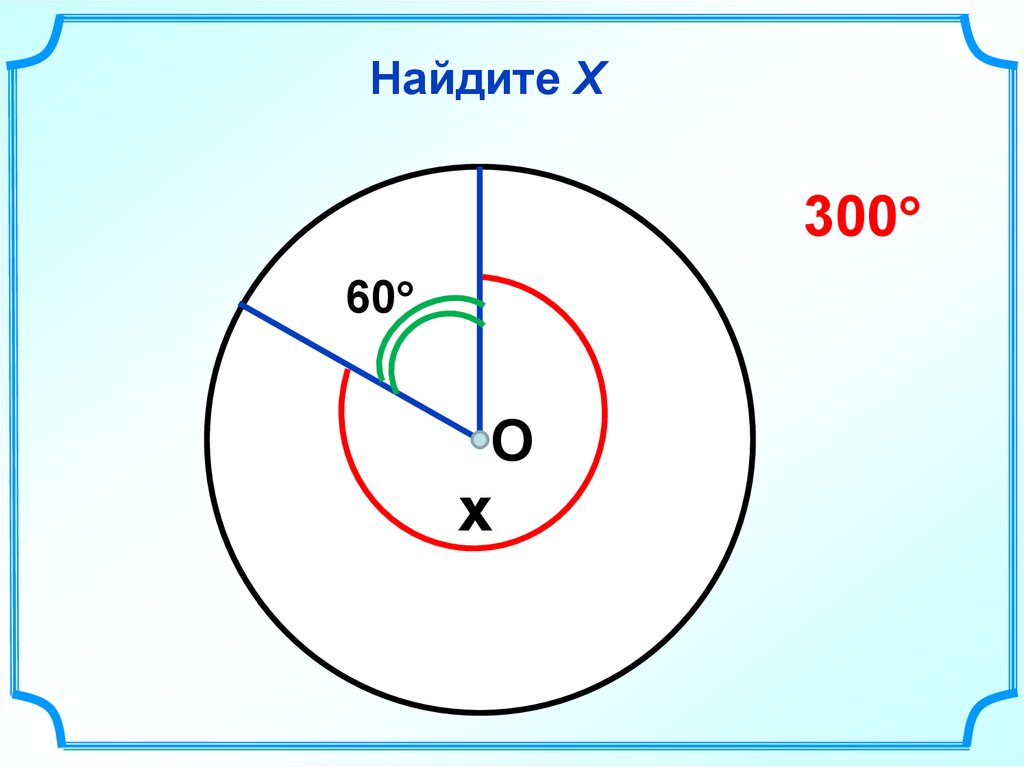
35. Найдите Х
30060
О
x
36. Найдите Х
240x
О
120
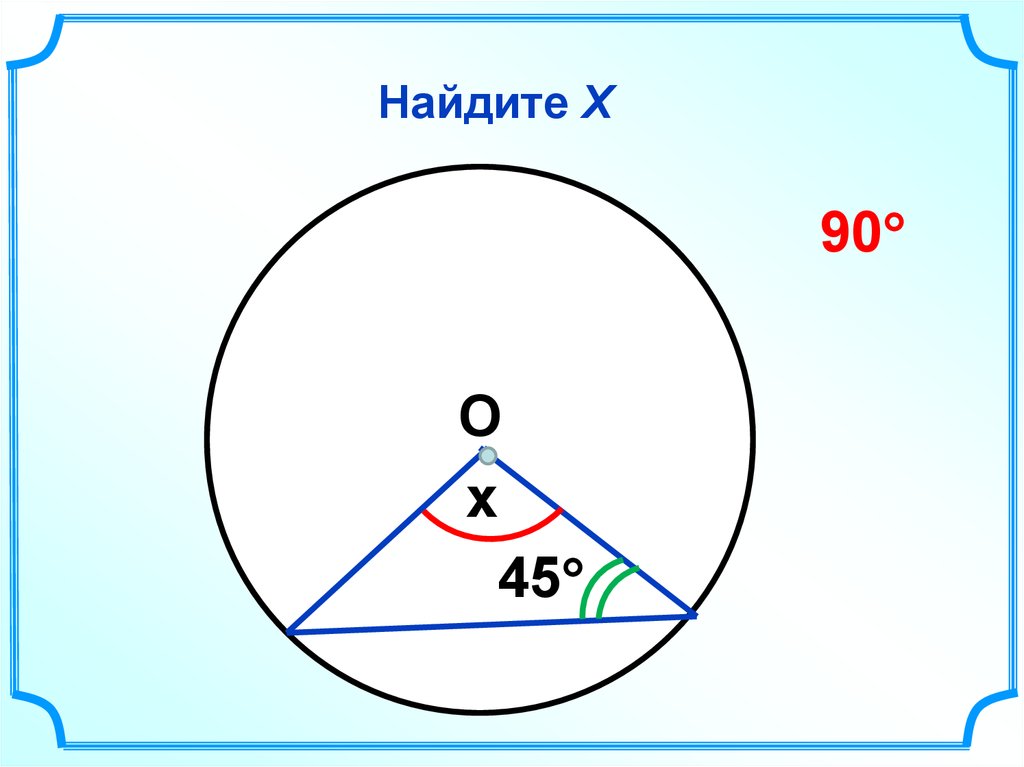
37. Найдите Х
90О
x
45
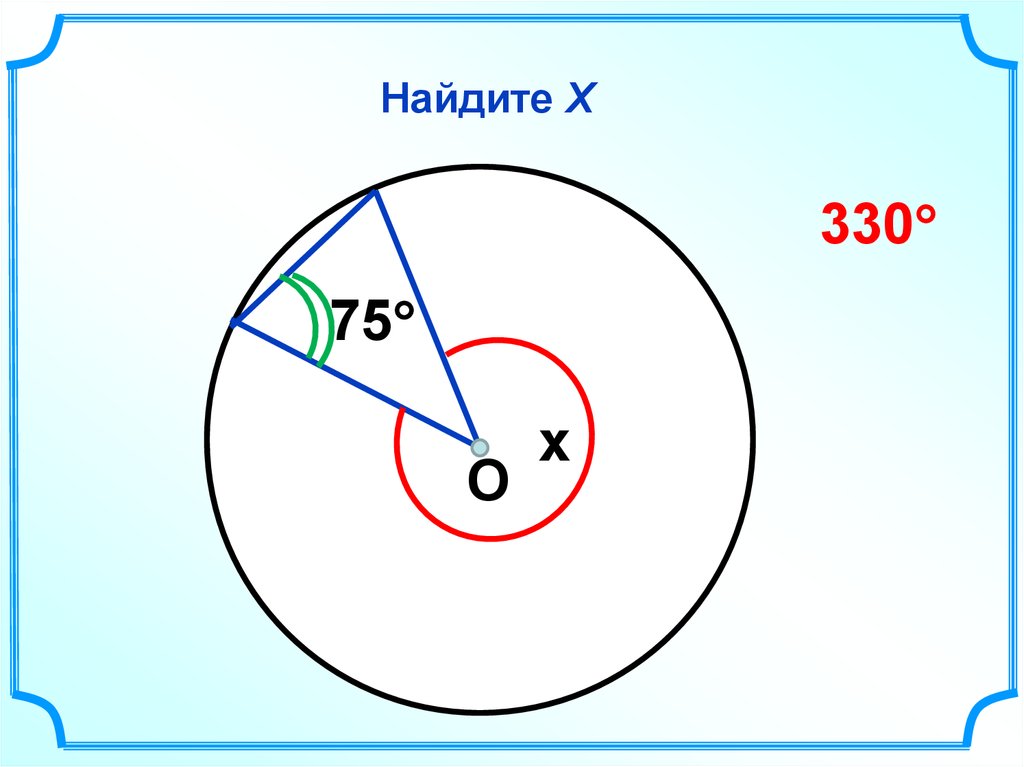
38. Найдите Х
33075
О
x
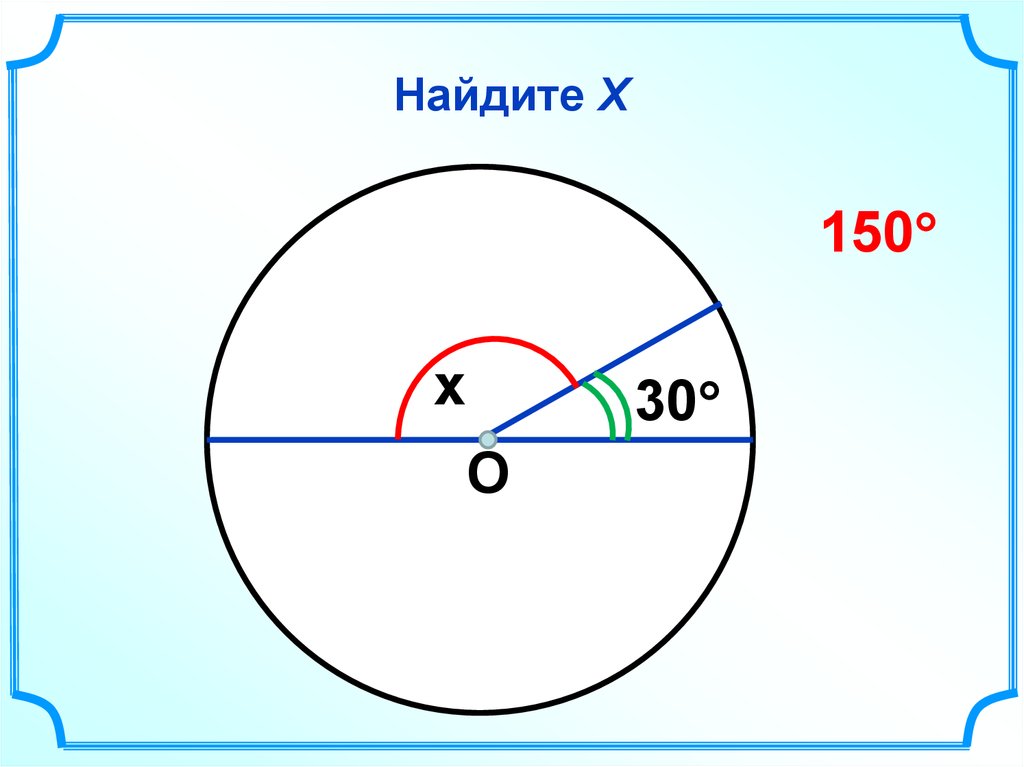
39. Найдите Х
150x
30
О
40. Найдите Х
13515
x
О
30
41. Найдите Х
55х
О
110
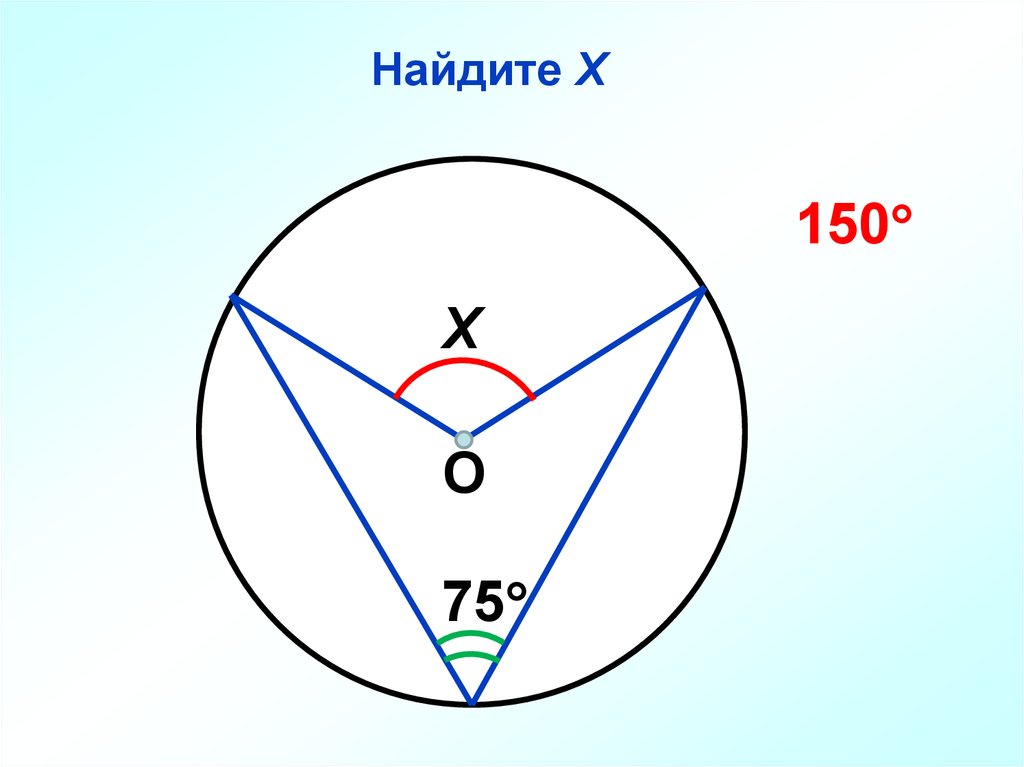
42.
Найдите Х150
Х
О
75
43.
Найдите Х60
30
Х
О
44.
Найдите Х16
О
32
Х
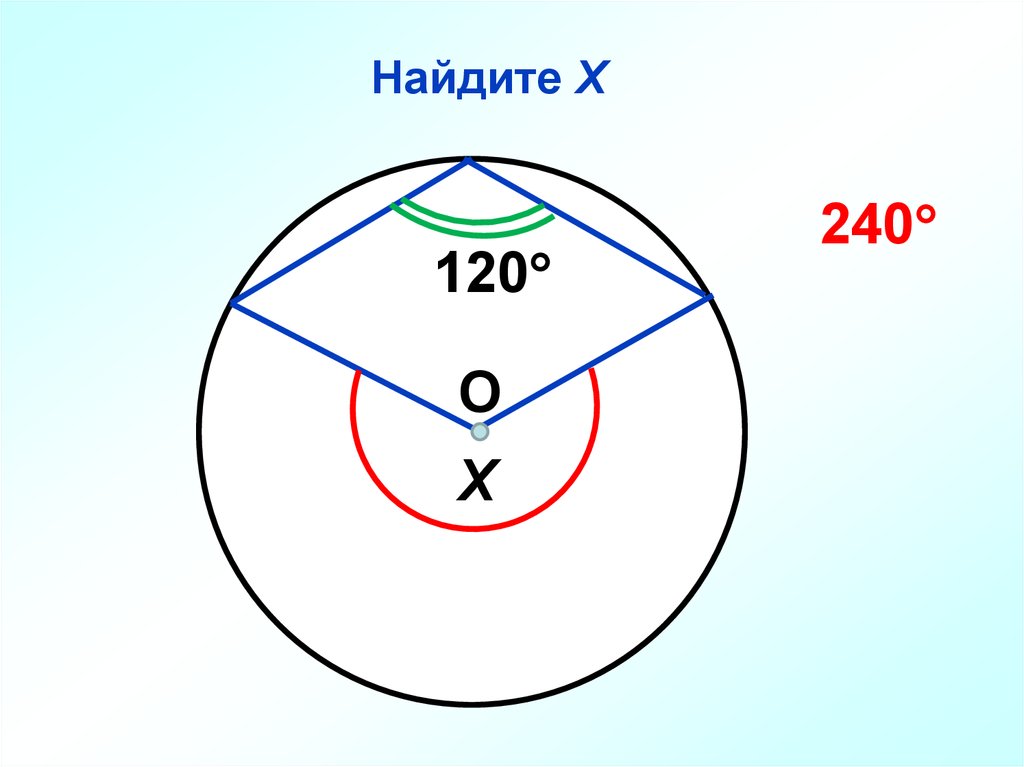
45.
Найдите Х120
О
Х
240
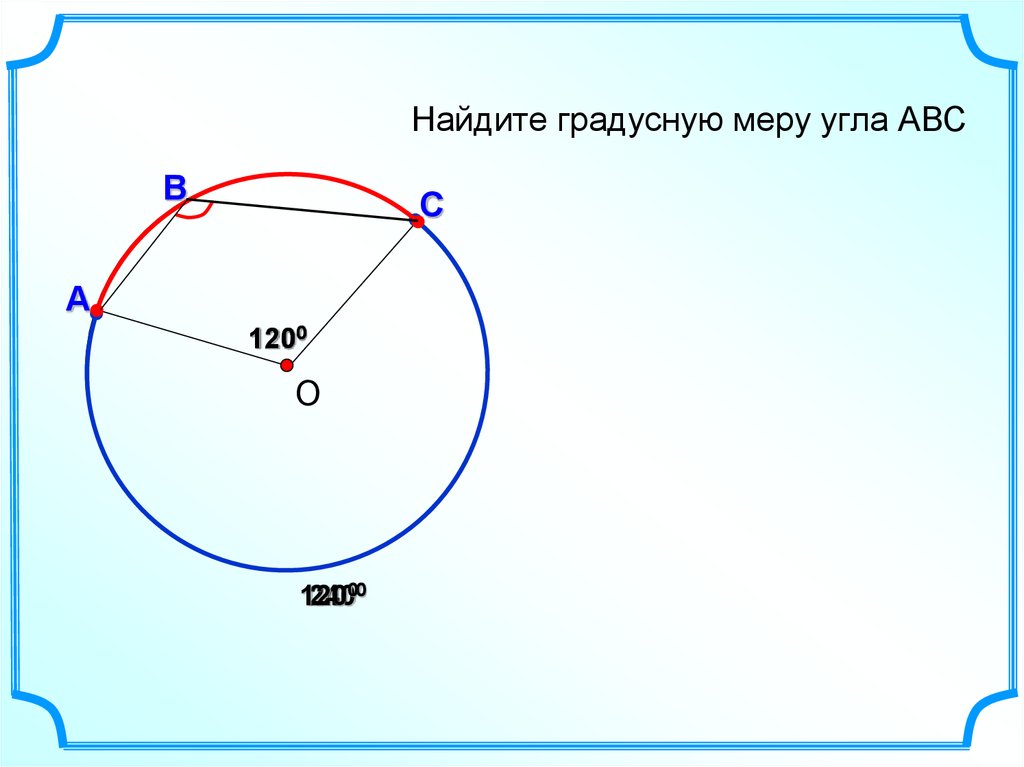
46.
Найдите градусную меру угла АВСВ
С
А
1200
О
120
24000
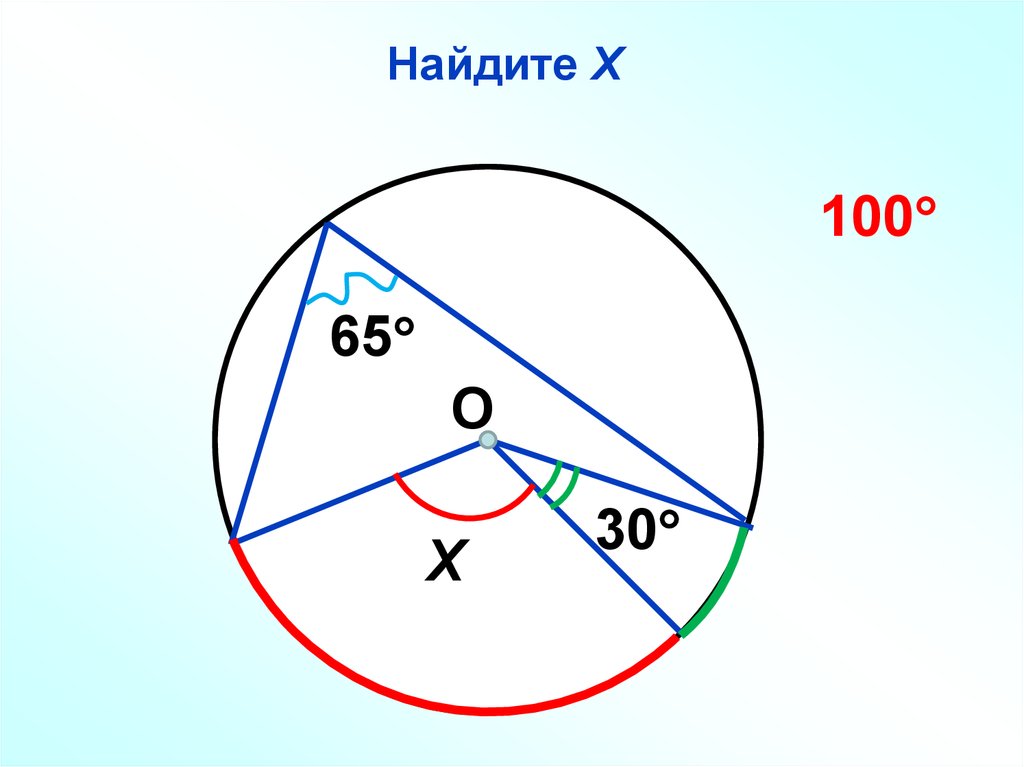
47.
Найдите Х100
65
О
Х
30
48.
Найдите градусную меру угла АВС.А
В
О
С
49.
1300Найдите градусную меру угла АВС
D
500
100
О
А
С
2600 В
50.
Найдите Х100
100
x
60
51. Найдите Х
50О
Х
80
52.
Найдите Х60
Х
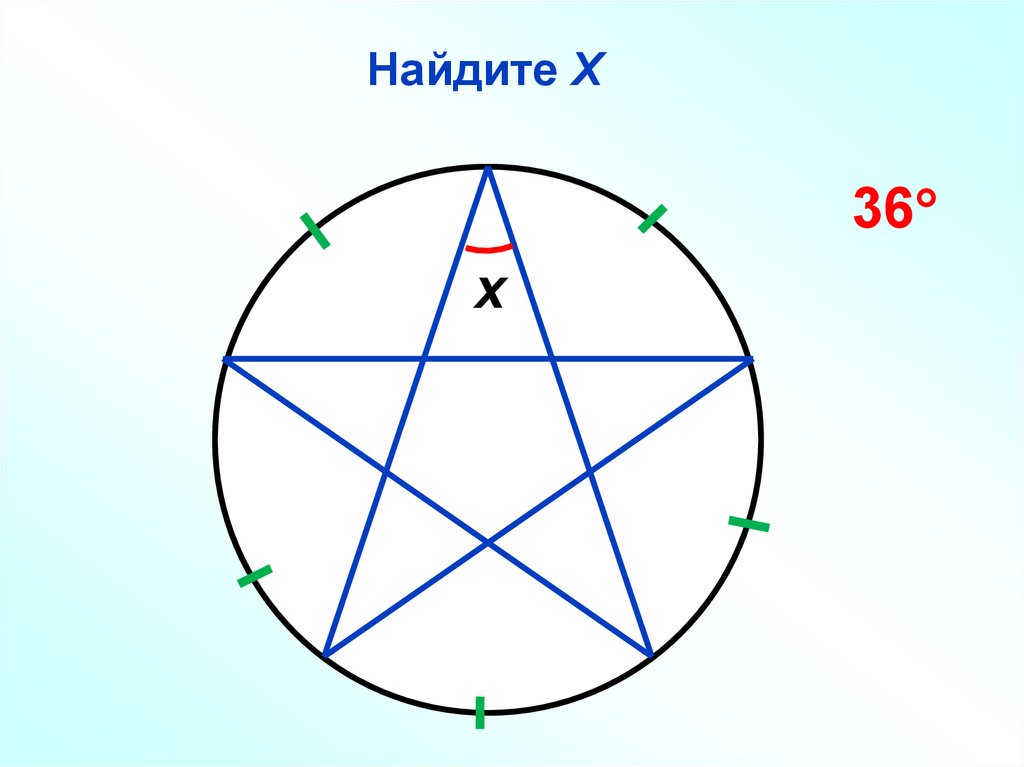
53.
Найдите Х36
x
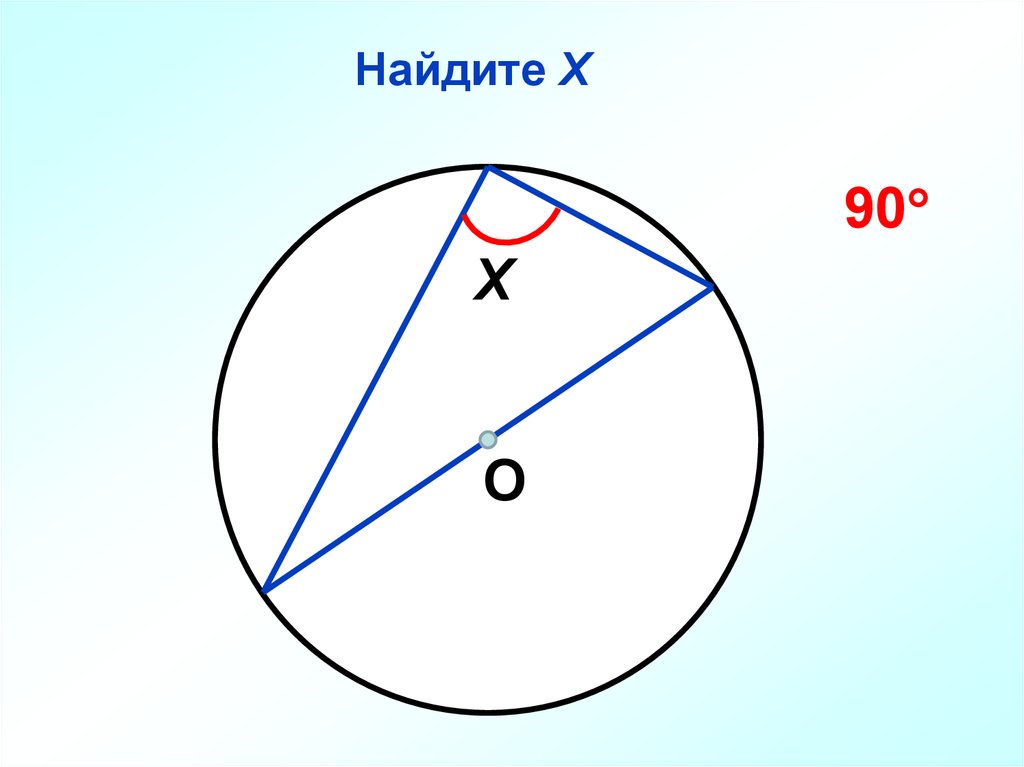
54.
Найдите Х90
Х
О
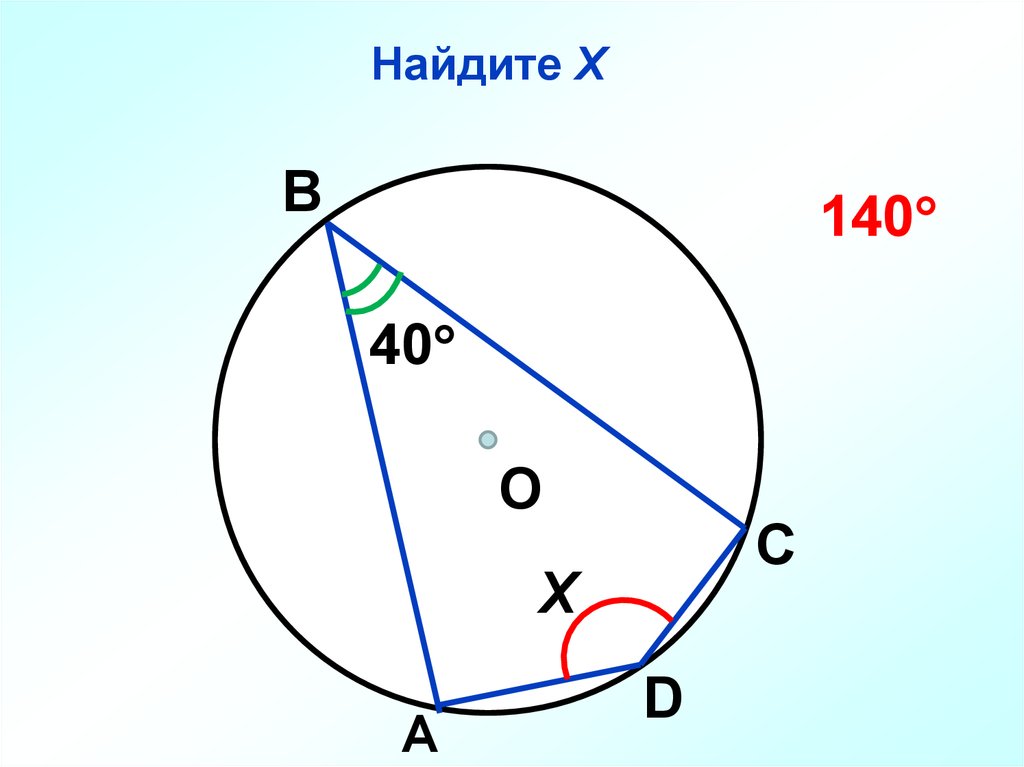
55.
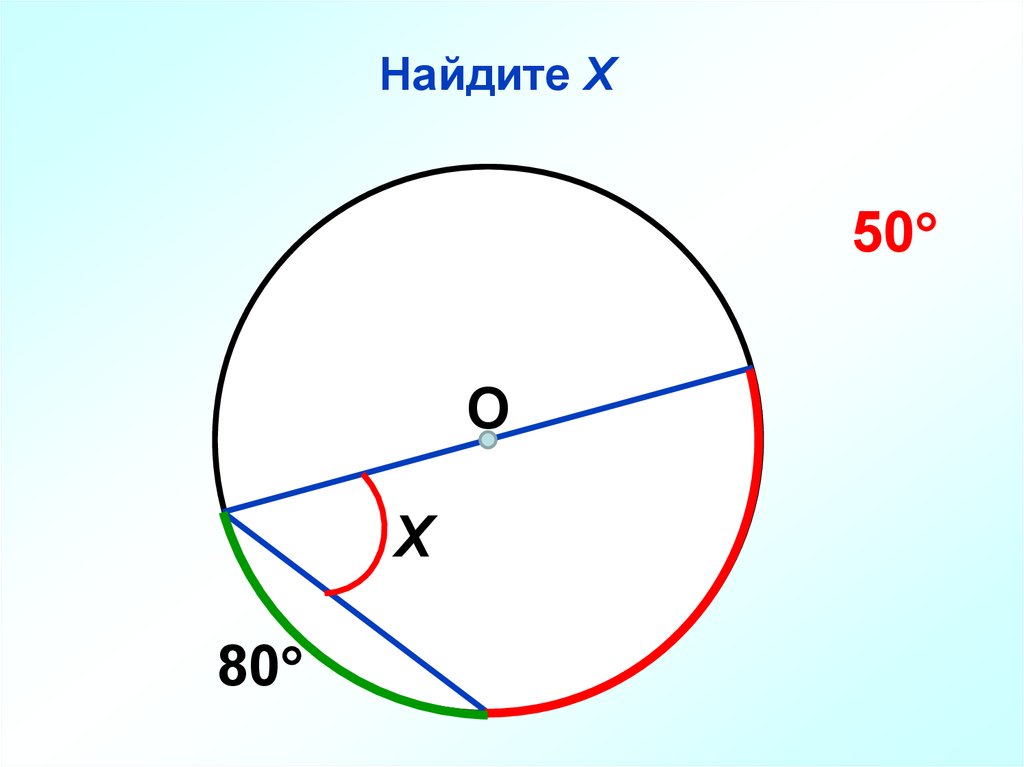
Найдите ХВ
140
40
О
С
Х
А
D
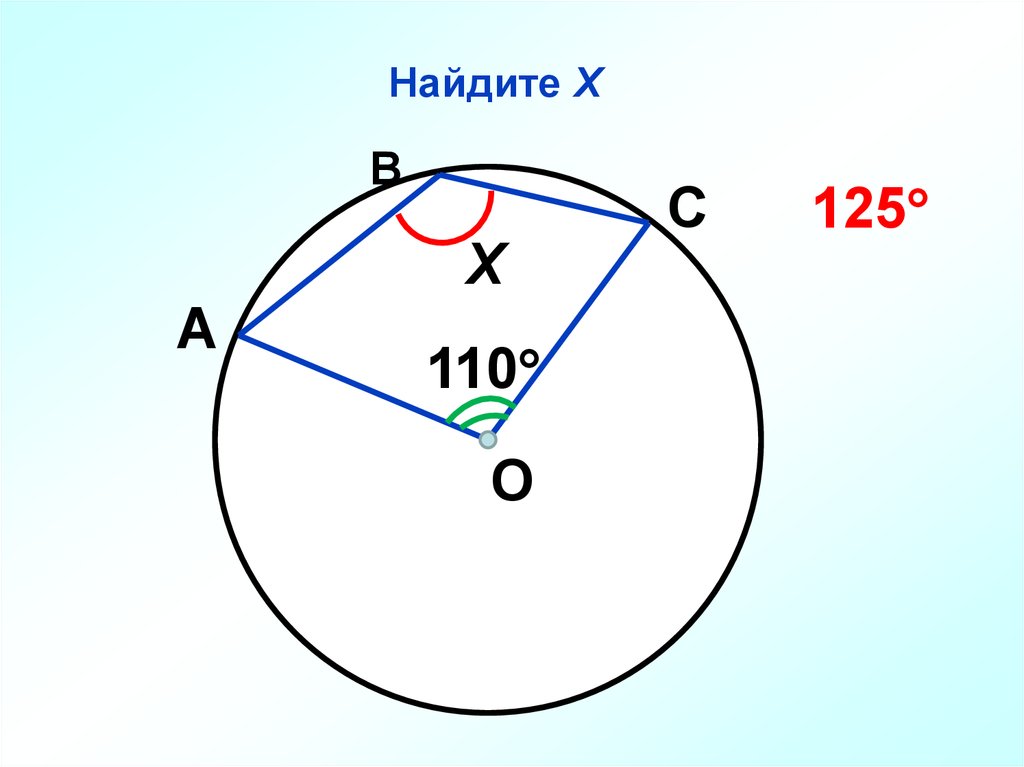
56. Найдите Х
ВХ
А
110
О
С
125
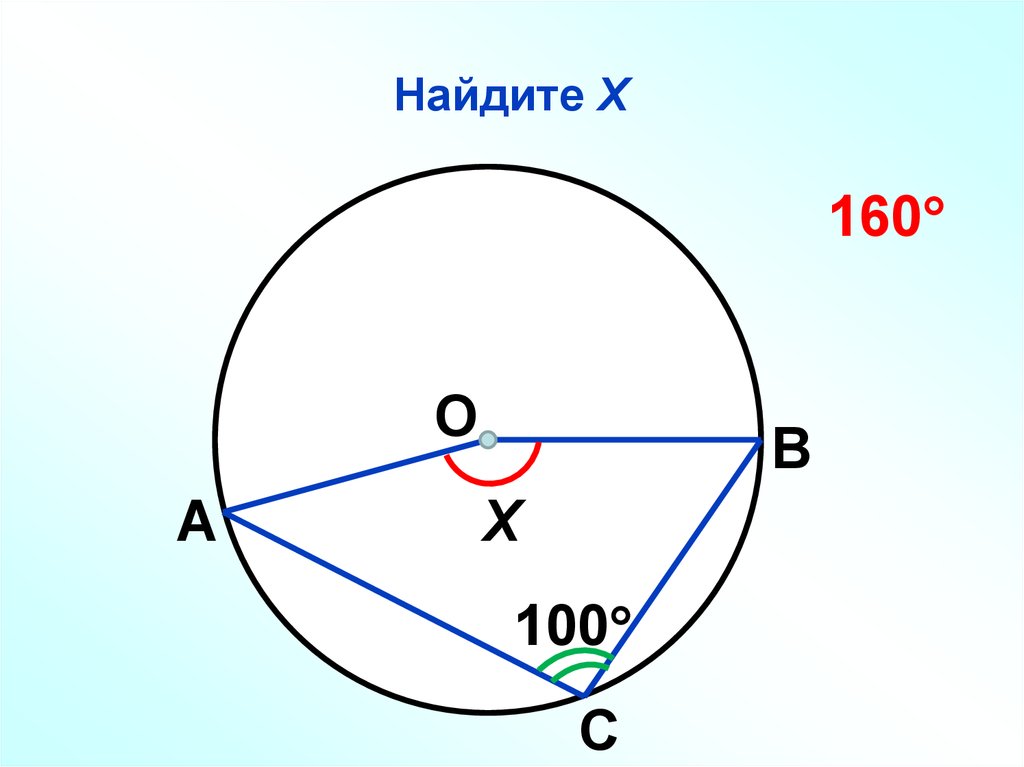
57. Найдите Х
160О
А
В
Х
100
С
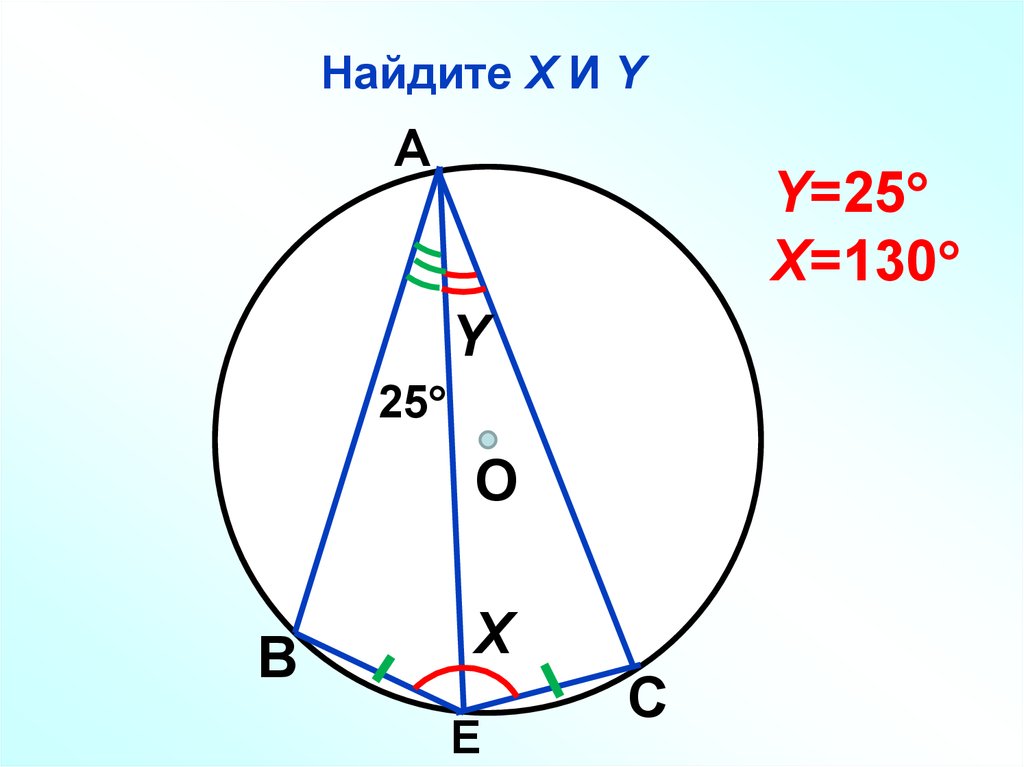
58. Найдите Х И Y
АY=25
Х=130
Y
25
О
В
Х
Е
С
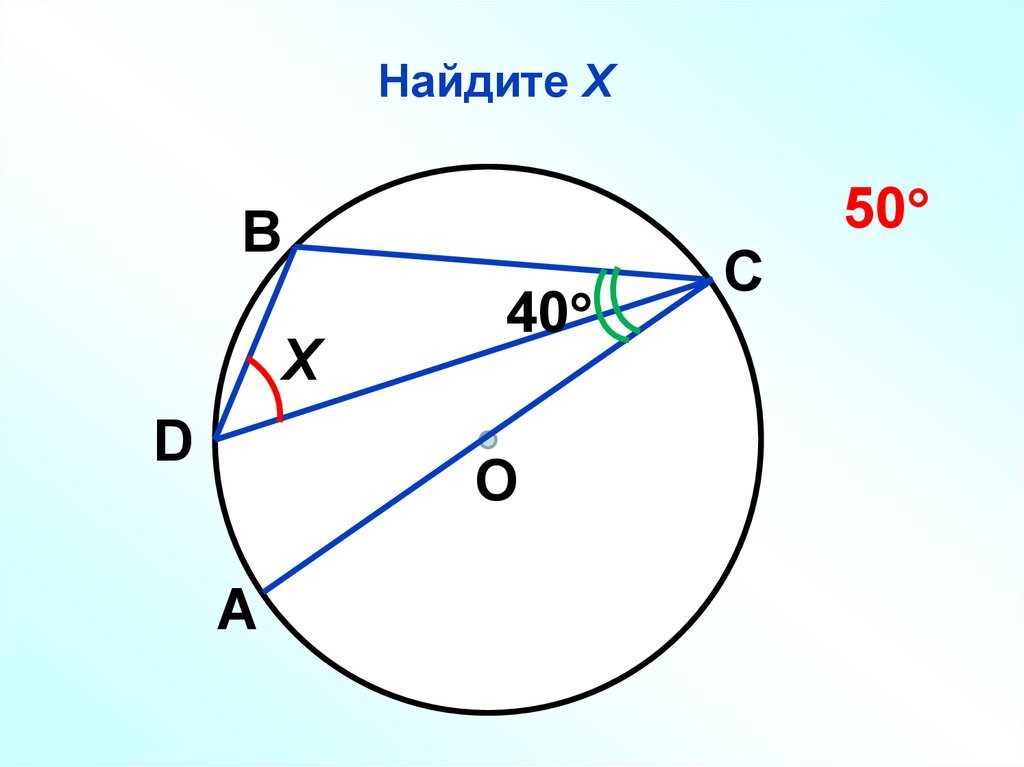
59. Найдите Х
50В
Х
D
40
О
А
С
60.
Дано:Окр. О, R
Найти: АOD, AСС
B
C
400
?
O
A
?
D
61.
Дано:Окр. О, R
Найти: ВСD
C
D
A
200
?
B
O
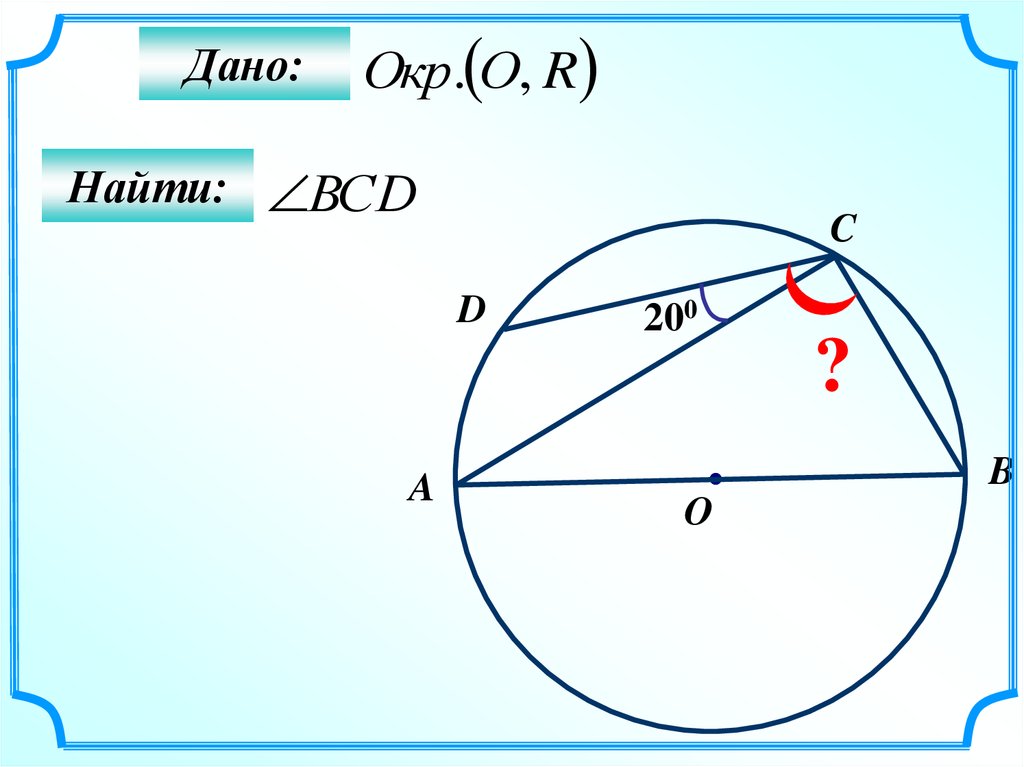
62.
Дано:Окр. О, R
Найти: ВСD
C
D
A
200
?
B
O
63.
Дано:Окр. О, R
Найти: ВAС
A
B
?
400
C
200
O
D
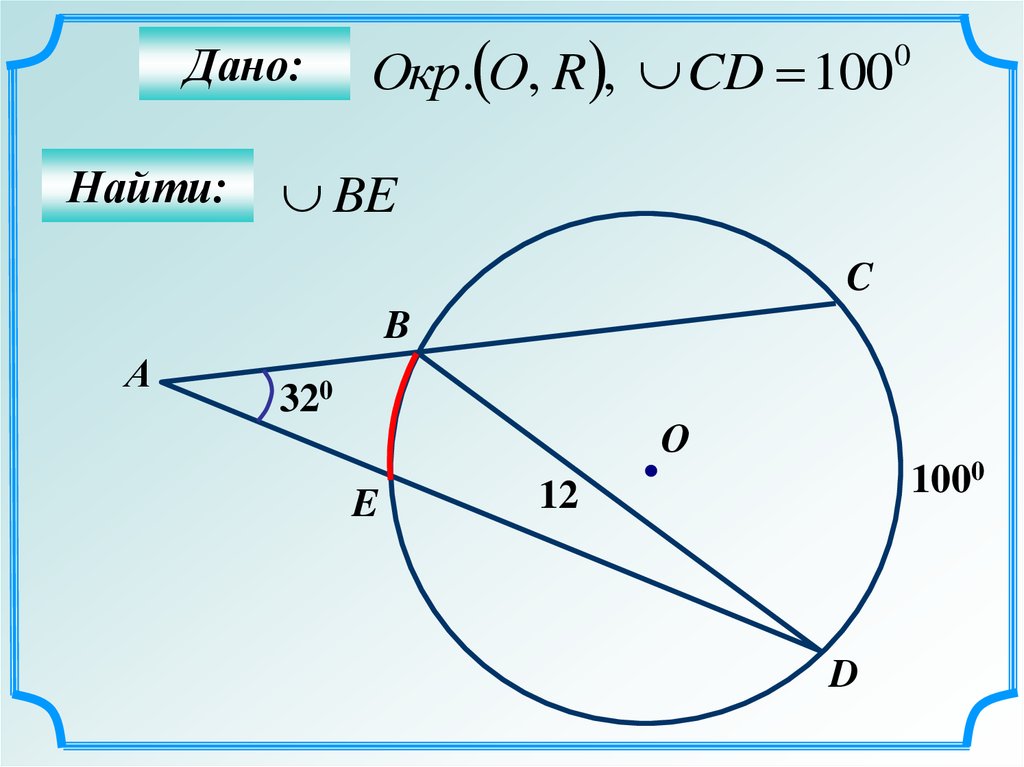
64.
Дано:Найти:
Окр. О, R , CD 100
0
BE
C
B
А
320
О
E
1000
12
D






















 mathematics
mathematics








