Similar presentations:
Углы, связанные с окружностью
1.
2.
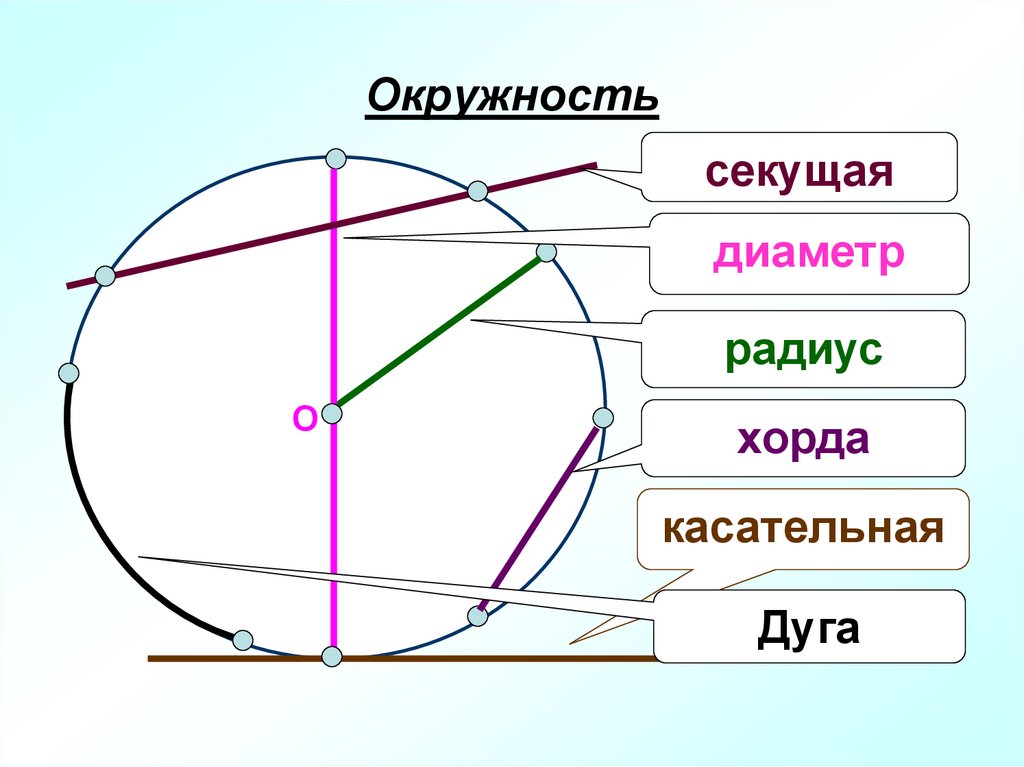
3. Окружность
секущаядиаметр
радиус
О
хорда
касательная
Дуга
4. Центральный угол
Оα
А
В
Угол с вершиной в центре
окружности называется
центральным углом
5. Вписанный угол
αУгол, вершина которого лежит на
окружности, а стороны пересекают
окружность, называется
вписанным углом
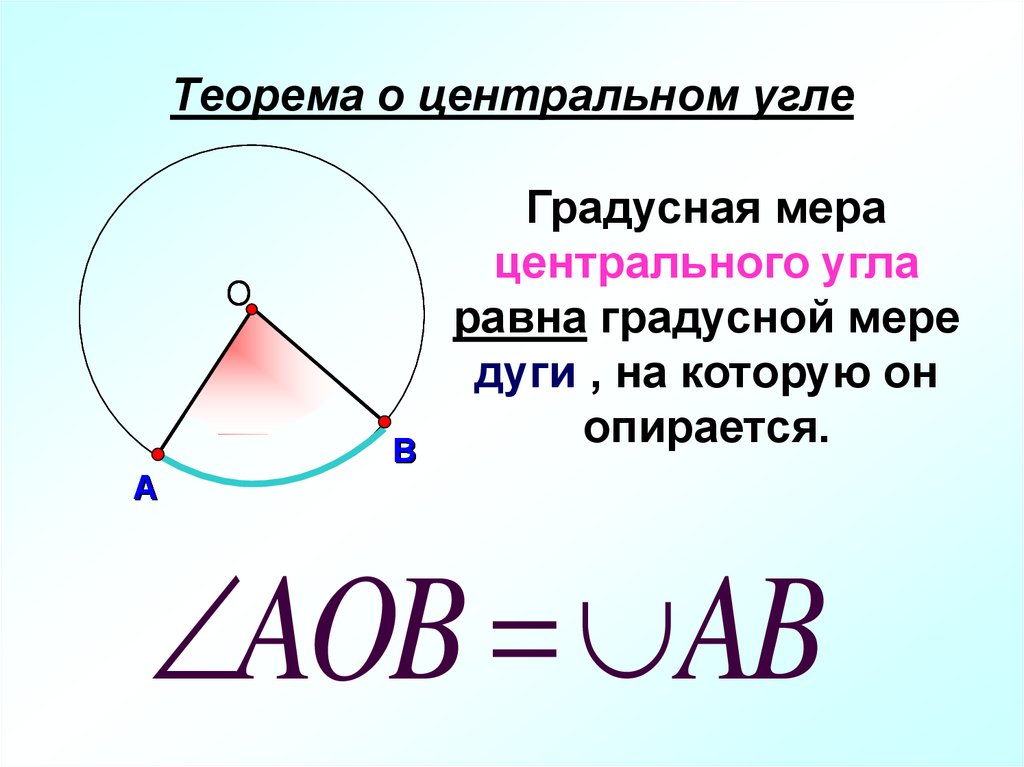
6. Теорема о центральном угле
ОА
В
Градусная мера
центрального угла
равна градусной мере
дуги , на которую он
опирается.
AOB AB
7. Теорема о вписанном угле
СВписанный угол
измеряется половиной
дуги, на которую он
опирается
О
А
В
1
ACB AB
2
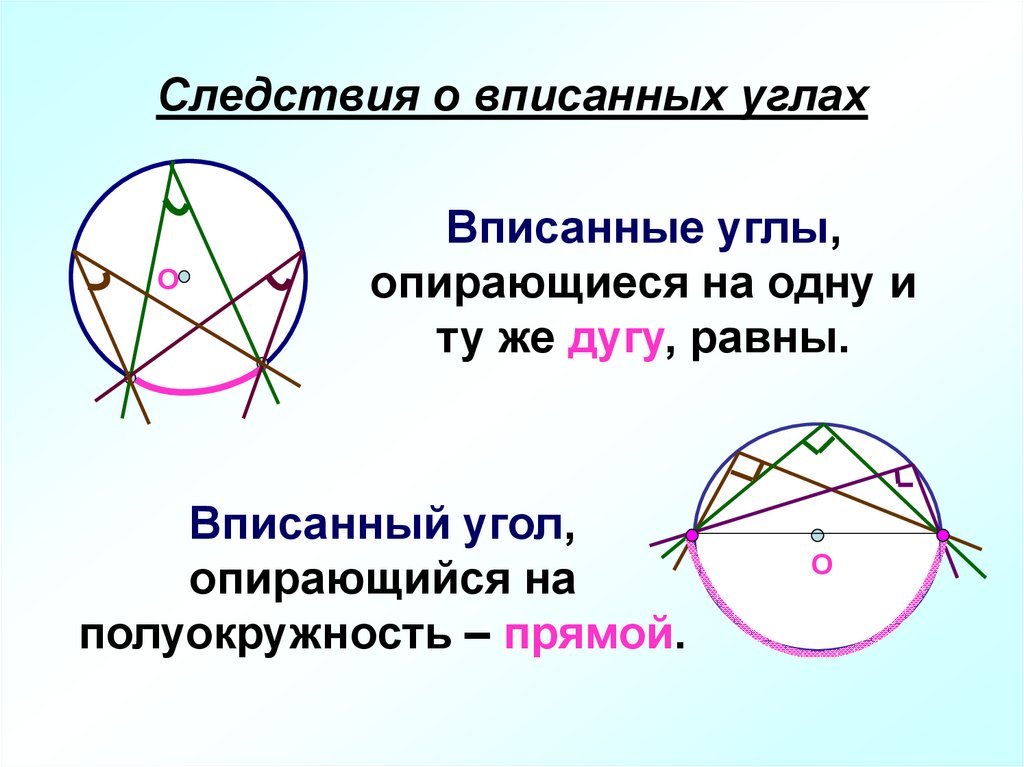
8. Следствия о вписанных углах
ОВписанные углы,
опирающиеся на одну и
ту же дугу, равны.
Вписанный угол,
опирающийся на
полуокружность – прямой.
О
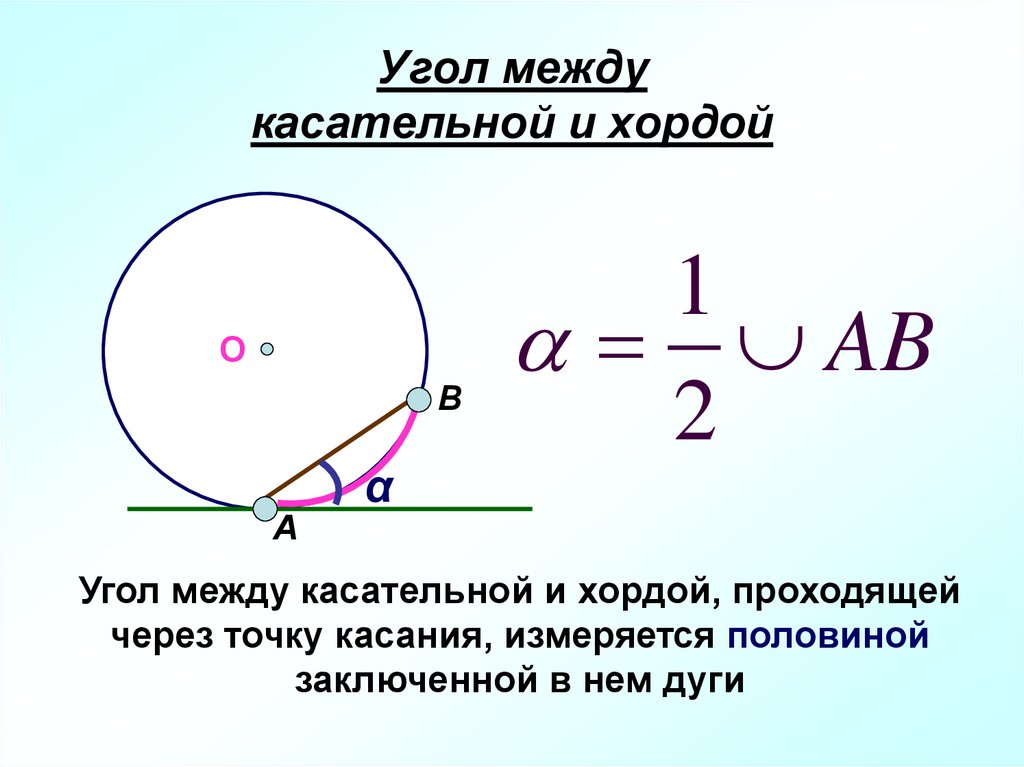
9. Угол между касательной и хордой
ОВ
А
1
AB
2
α
Угол между касательной и хордой, проходящей
через точку касания, измеряется половиной
заключенной в нем дуги
10. Угол между двумя пересекающимися хордами
1AC BD
2
А
О
D
α
С
В
Угол между двумя пересекающимися
хордами измеряется полусуммой
заключенных между ними дуг
11. Угол между двумя секущими, проведенными из одной точки
1CE BD
2
C
B
О
α
E
D
А
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
12. Угол между касательной и секущей, проведенными из одной точки
BО
D
C
1
BD BC
2
α
A
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
13. Угол между двумя касательными, проведенными из одной точки
BО
α
180 BC
0
A
C
Угол между двумя касательными, проведенными из
одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.
14. Устные задания
1N
î êð.(O, R )
Дано:
MKE
MNE
в 2 раза
MKE , MNE
Найти:
О
M
E
K
2
Дано:
î êð.(O, R )
Найти:
ABC
Дано:
3
î êð.(O, R )
Найти:
BEC
B
C
700
A
O
O
520
1000
A
C
D
B
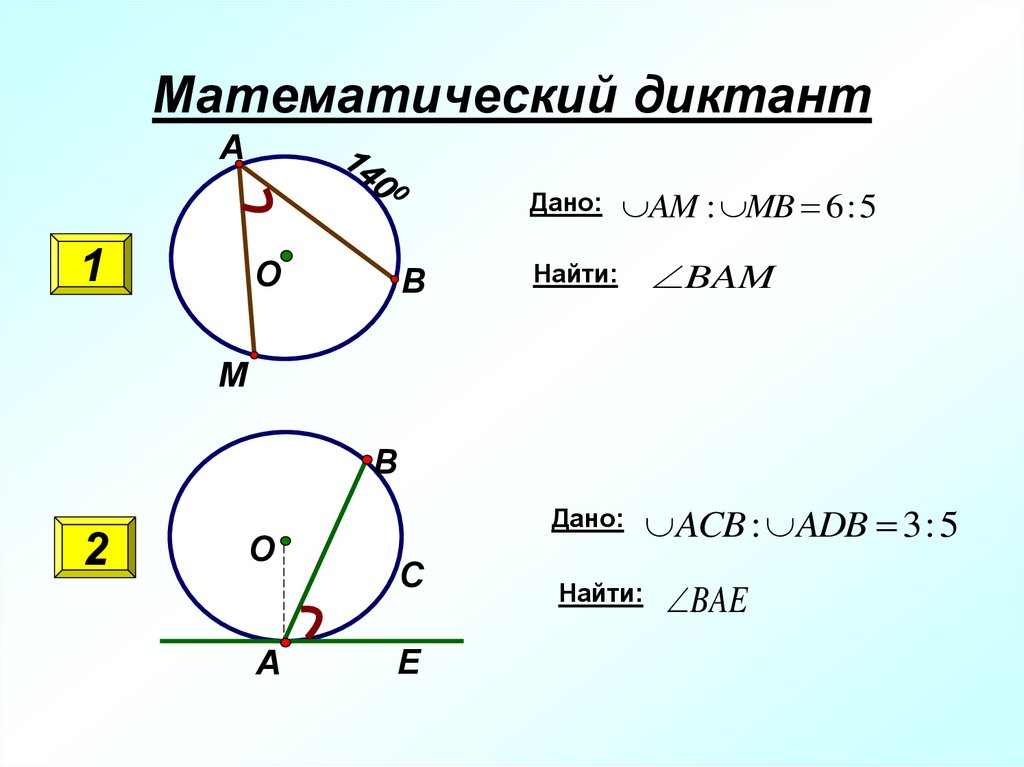
15. Математический диктант
АДано:
1
О
В
AM : MB 6:5
Найти:
BAM
М
В
2
О
А
Дано:
С
Е
Найти:
ACB : ADB 3: 5
BAE
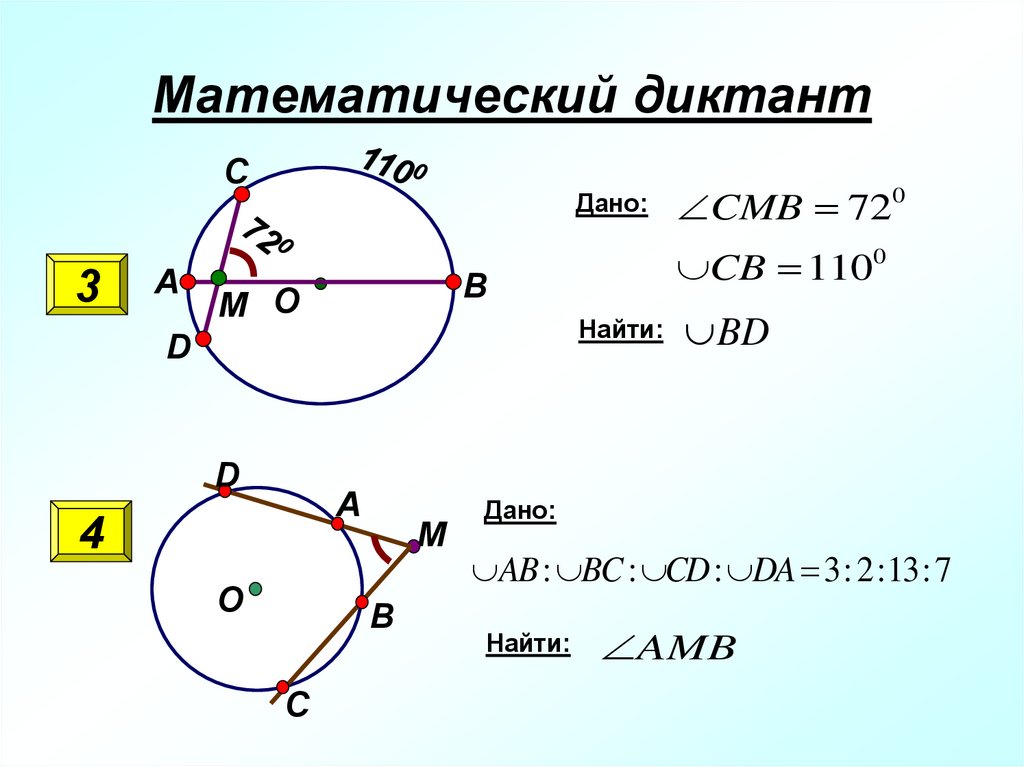
16. Математический диктант
С3
А
Дано:
Найти:
D
D
А
4
О
M
B
C
CB 1100
В
M О
CMB 720
BD
Дано:
AB : BC : CD : DA 3: 2:13: 7
Найти:
AMB
17. Математический диктант
5Дано:
C
D
O
A
B
BDC 112
0
BD : DC 7 : 9
Найти: BAD
18. Решение задач
1К
А
Дано:
АМ – биссектриса угла ВАС
װЕ
О
BAC - вписанный
МК װАС
lll
В
Доказать: МК = АВ
Доказательство:
М
С
3) Проведем
1)Ò.ê. AC MK , ò î MAC AMK
2) AEM ðàâí î áåäðåí í û é ( AE EM )
BK ; AMK ABK (опираются на ÀÊ )
4) BAM BKM (опираются на BM )
5) BEK ðàâí î áåäðåí í û é ( ÂÅ ÅÊ )
6) МК = АВ
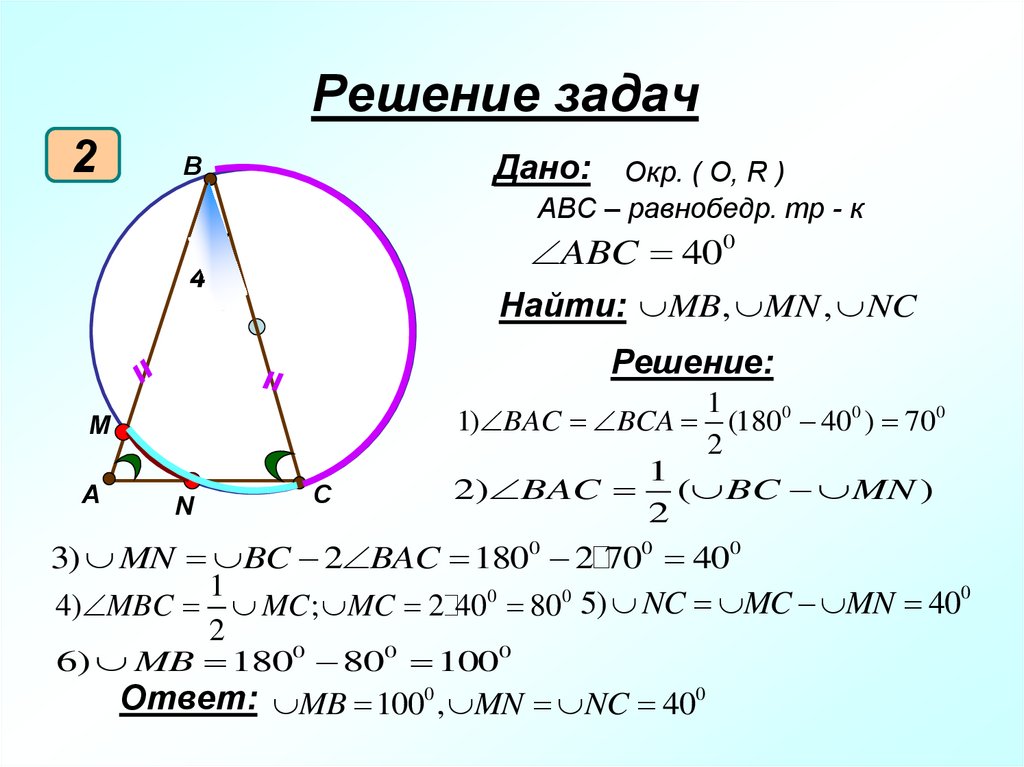
19. Решение задач
2Дано: Окр. ( О, R )
B
ABC – равнобедр. тр - к
ABC 400
Найти: MB, MN , NC
400
Решение:
M
1) BAC BCA
A
2) BAC
N
C
1
(1800 400 ) 700
2
1
( BC MN )
2
3) MN BC 2 BAC 1800 2 700 400
1
0
4) MBC MC ; MC 2 400 800 5) NC MC MN 40
2
6) MB 1800 800 1000
Ответ: MB 1000 , MN NC 400
20. Итог урока
Закончи фразу1) Угол между касательной и хордой, проходящей
через точку касания, измеряется …
2) Угол между двумя пересекающимися хордами
измеряется …
3) Угол между двумя секущими, проведенными из
одной точки, измеряется …
4) Угол между касательной и секущей,
проведенными из одной точки, измеряется …
5) Угол между двумя касательными, проведенными
из одной точки, равен …
21.
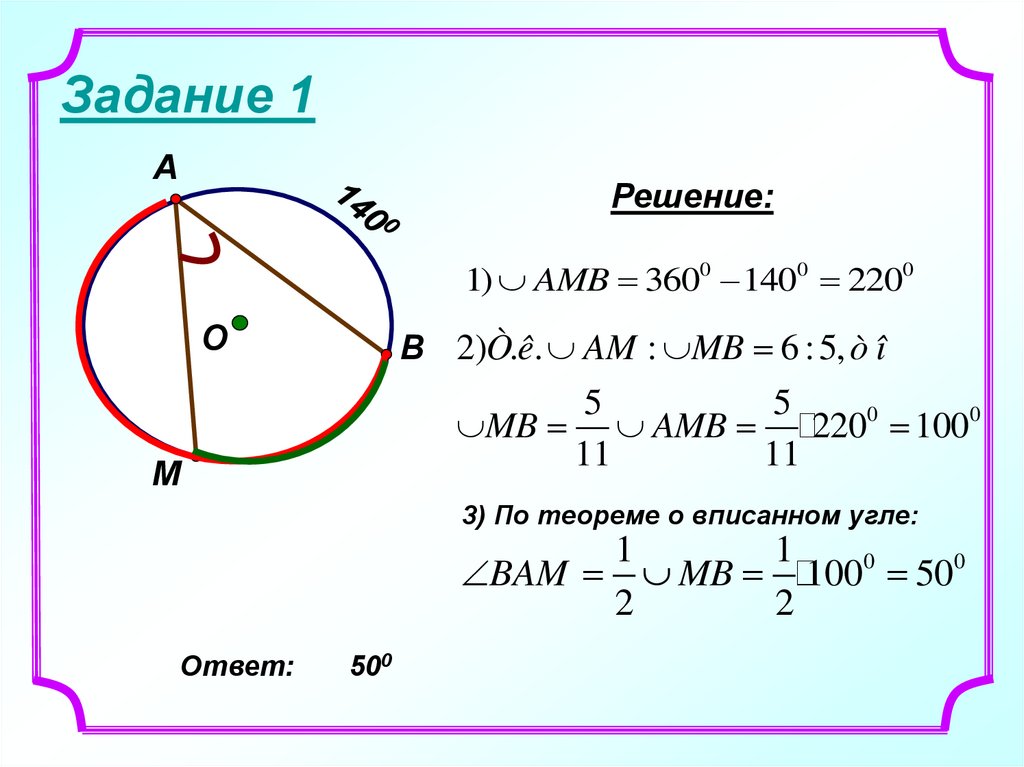
22. Задание 1
АРешение:
1) AMB 3600 1400 2200
О
В 2)Ò.ê. AM : MB 6 : 5, ò î
5
5
MB AMB
2200 1000
11
11
М
3) По теореме о вписанном угле:
1
1
BAM MB 1000 500
2
2
Ответ:
500
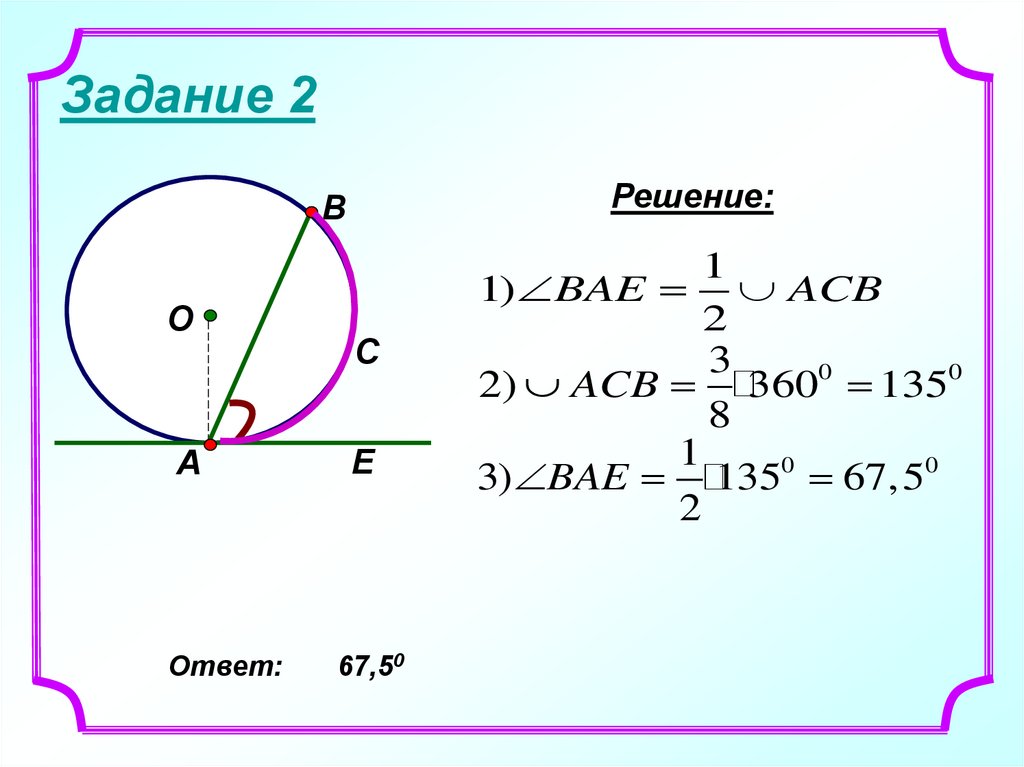
23. Задание 2
Решение:В
О
А
Ответ:
С
Е
67,50
1
1) BAE ACB
2
3
2) ACB 3600 1350
8
1
3) BAE 1350 67, 50
2
24. Задание 3
СА
M
Решение:
В
О
1
1) CMB BC AD
2
2) AD 2 CMB BC
AD 2 720 1100 340
D
3) BD ADB AD
BD 180 34 146
0
Ответ:
1460
0
0
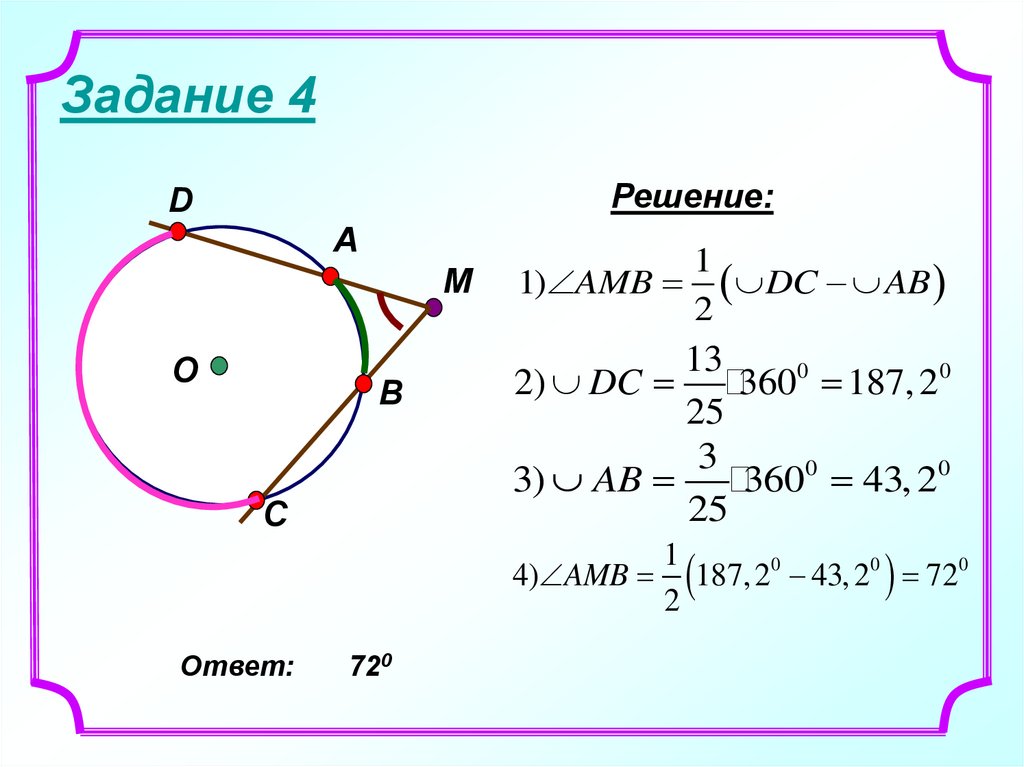
25. Задание 4
Решение:D
А
M
О
B
C
1
1) AMB DC AB
2
13
2) DC
3600 187, 20
25
3
3) AB
3600 43, 20
25
4) AMB
Ответ:
720
1
187, 20 43, 20 720
2
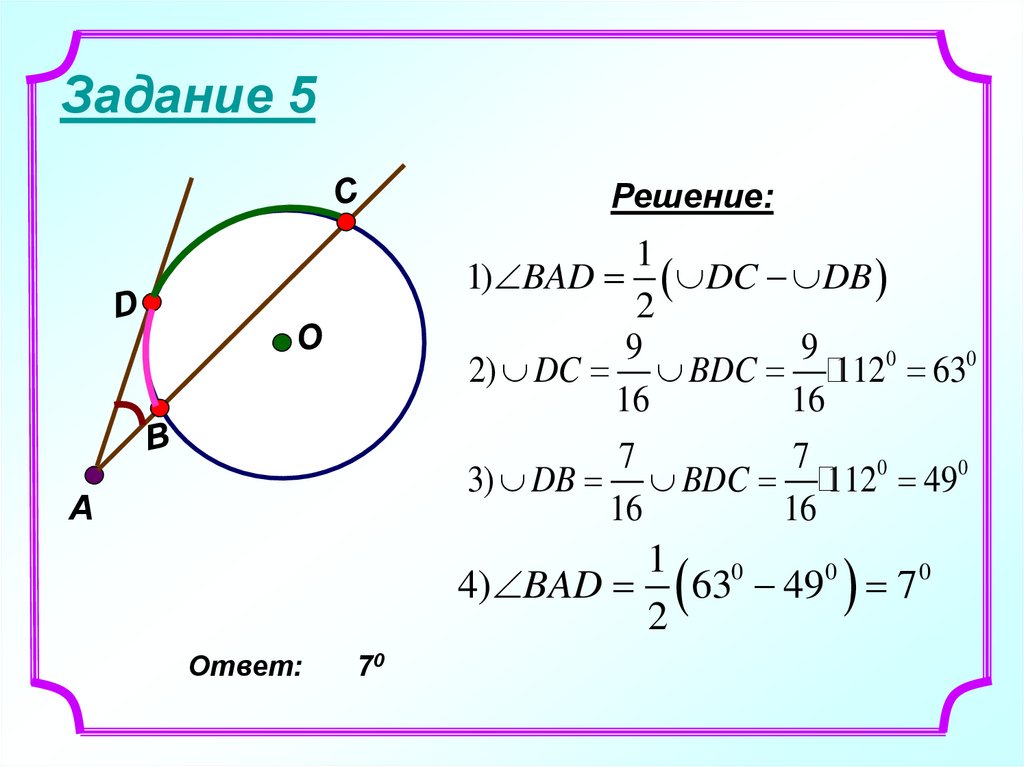
26. Задание 5
Решение:1
1) BAD DC DB
2
9
9
2) DC BDC 1120 630
16
16
7
7
3) DB BDC 1120 490
16
16
A
1
4) BAD 630 490 7 0
2
Ответ:
70















 mathematics
mathematics








