Similar presentations:
Углы, связанные с окружности. Окружность
1.
2.
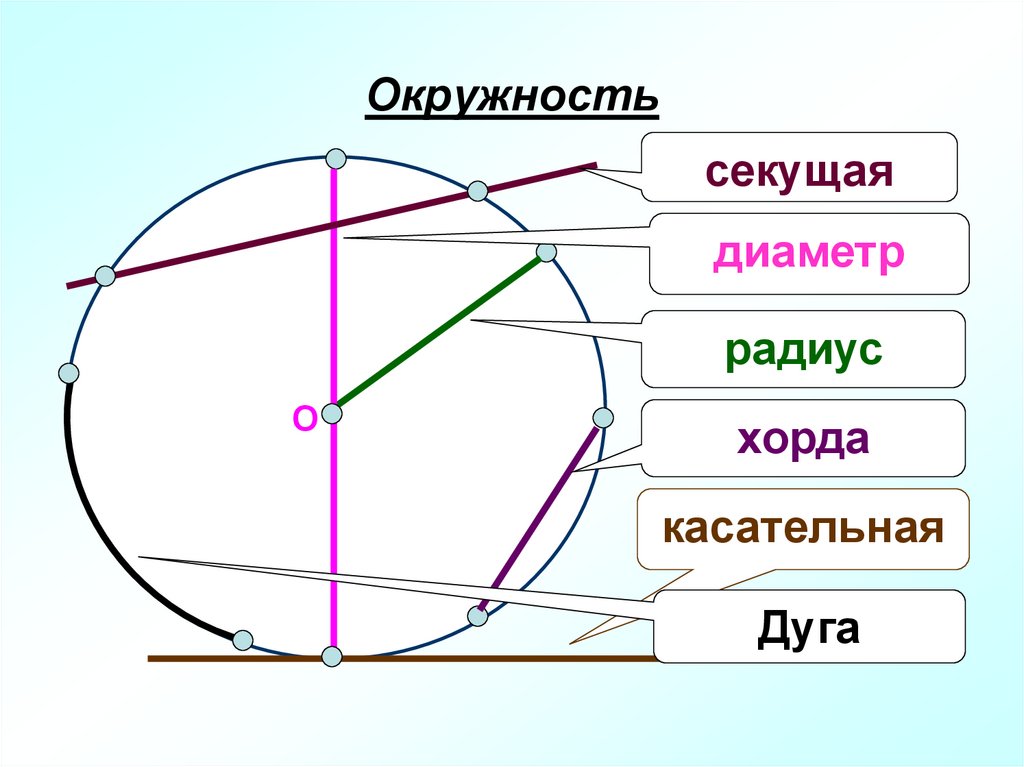
3. Окружность
секущаядиаметр
радиус
О
хорда
касательная
Дуга
4. Центральный угол
Оα
А
В
Угол с вершиной в центре
окружности называется
центральным углом
5. Вписанный угол
αУгол, вершина которого лежит на
окружности, а стороны пересекают
окружность, называется
вписанным углом
6. Теорема о центральном угле
ОА
В
Градусная мера
центрального угла
равна градусной мере
дуги , на которую он
опирается.
AOB AB
7. Теорема о вписанном угле
СВписанный угол
измеряется половиной
дуги, на которую он
опирается
О
А
В
1
ACB AB
2
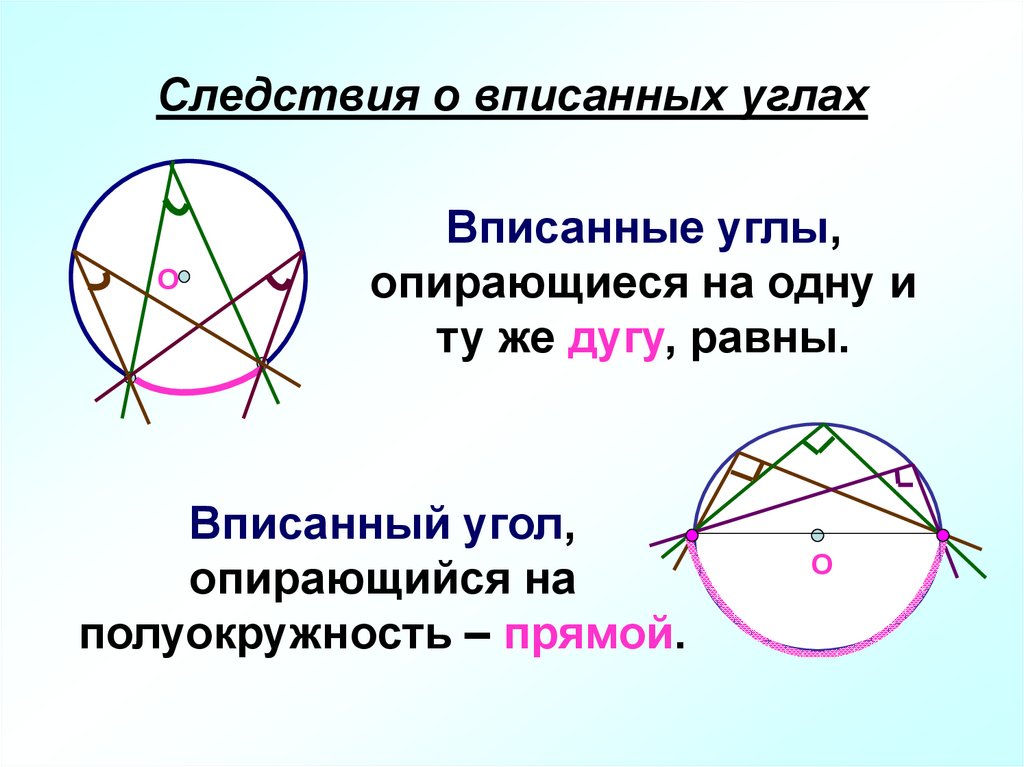
8. Следствия о вписанных углах
ОВписанные углы,
опирающиеся на одну и
ту же дугу, равны.
Вписанный угол,
опирающийся на
полуокружность – прямой.
О
9. Угол между касательной и хордой
ОВ
А
1
AB
2
α
Угол между касательной и хордой, проходящей
через точку касания, измеряется половиной
заключенной в нем дуги
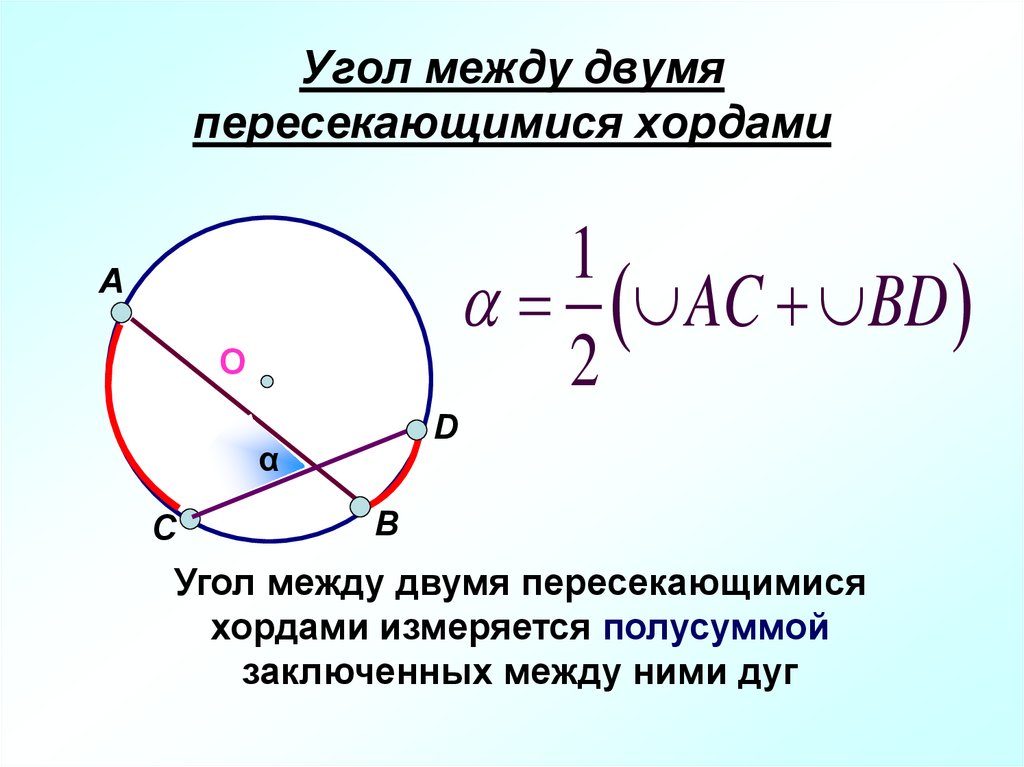
10. Угол между двумя пересекающимися хордами
1AC BD
2
А
О
D
α
С
В
Угол между двумя пересекающимися
хордами измеряется полусуммой
заключенных между ними дуг
11. Угол между двумя секущими, проведенными из одной точки
1CE BD
2
C
B
О
α
E
D
А
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
12. Угол между касательной и секущей, проведенными из одной точки
О1
B
BD BC
2
D
C
α
A
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
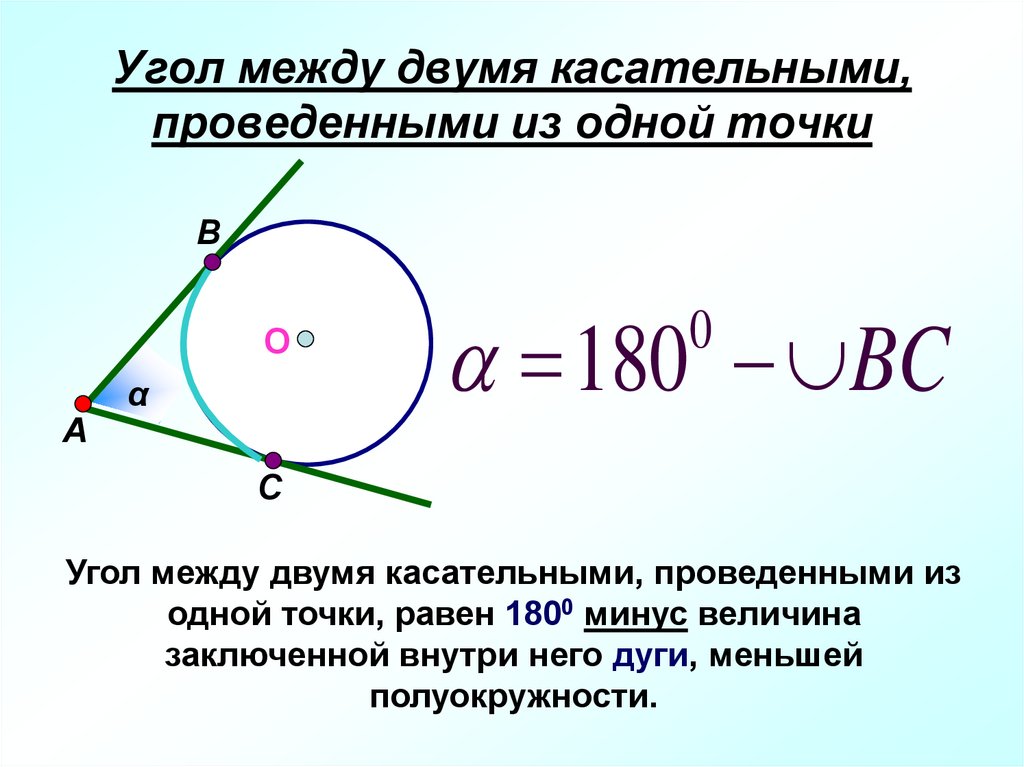
13. Угол между двумя касательными, проведенными из одной точки
BО
α
180 BC
0
A
C
Угол между двумя касательными, проведенными из
одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.









 mathematics
mathematics








