Similar presentations:
Центральные и вписанные углы
1. I «Центральные и вписанные углы». 8 класс.
I«Центральные и вписанные углы».
8 класс.
Давыдова Галина Анатольевна,
МКОУ «Кукуйская ООШ №25»
учитель математики
2. Цель работы:
• Совершенствование навыков решениязадач на применение теоремы о вписанном
угле и ее следствий.
Задачи:
• Систематизировать теоретический
материал по теме «Центральный и
вписанный углы»;
• Совершенствовать навыки решения задач
по данной теме.
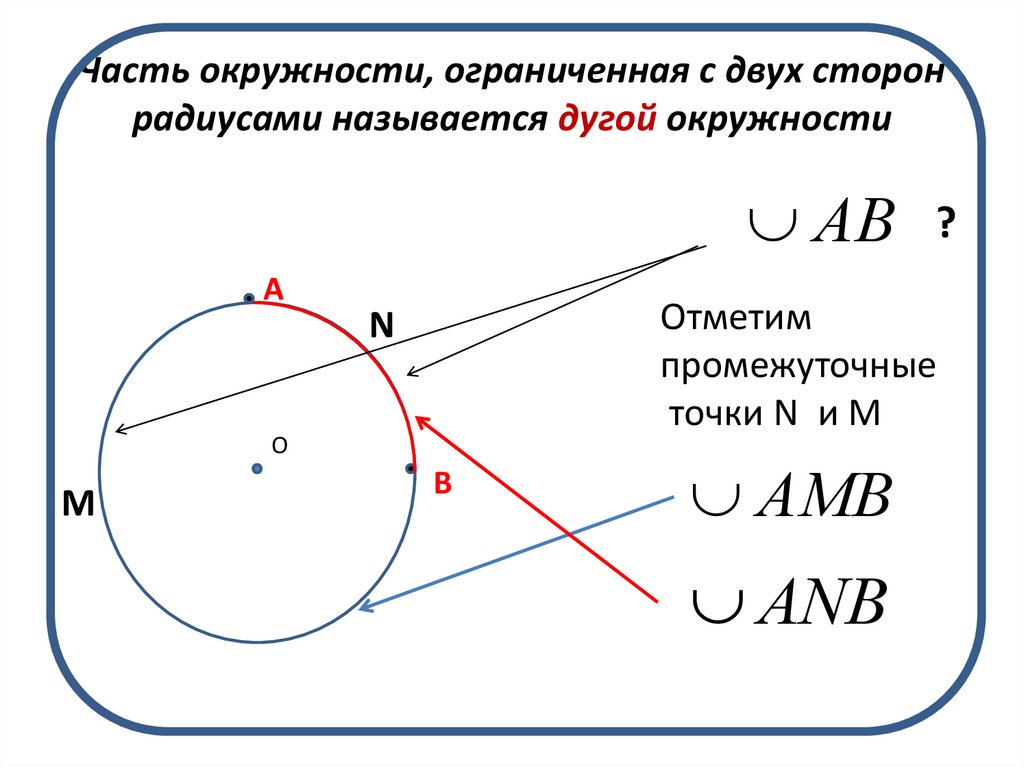
3. Часть окружности, ограниченная с двух сторон радиусами называется дугой окружности
АВА
Отметим
промежуточные
точки N и M
N
О
M
?
В
АМВ
АNВ
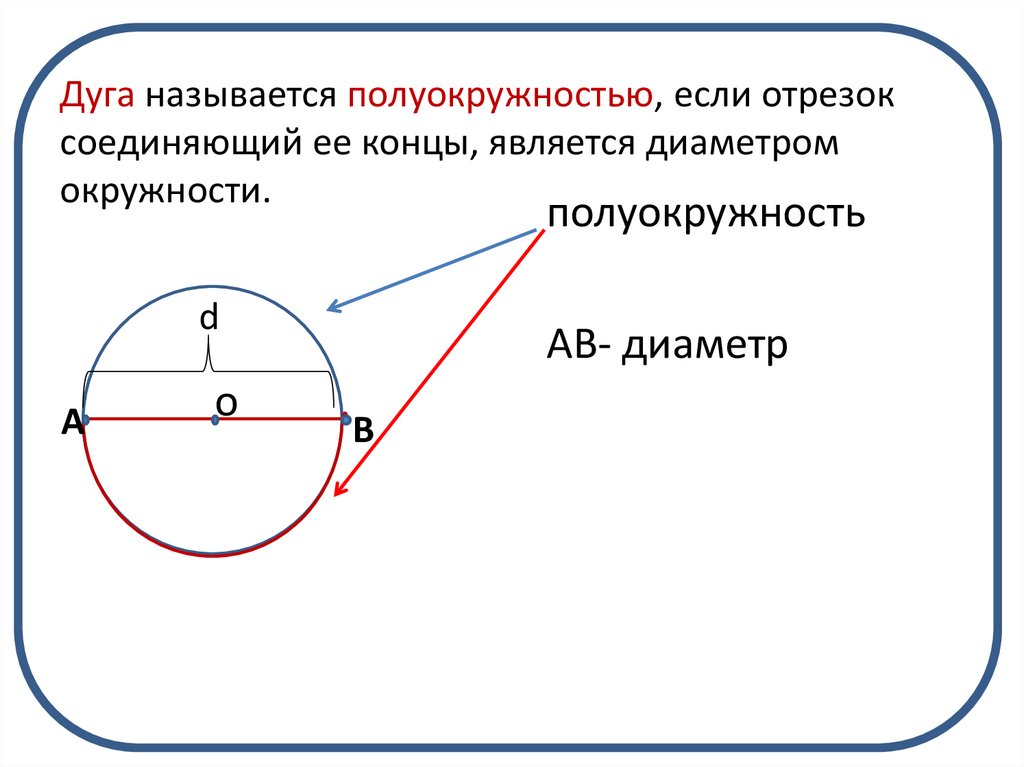
4. Дуга называется полуокружностью, если отрезок соединяющий ее концы, является диаметром окружности.
полуокружностьd
А
о
АВ- диаметр
В
5. Центральный угол
АО
АВ = < АОВ
В
• Угол с вершиной в
центре окружности
называется ее
центральным
углом.
• Градусная мера
дуги АВ равна
градусной мере
угла АОВ
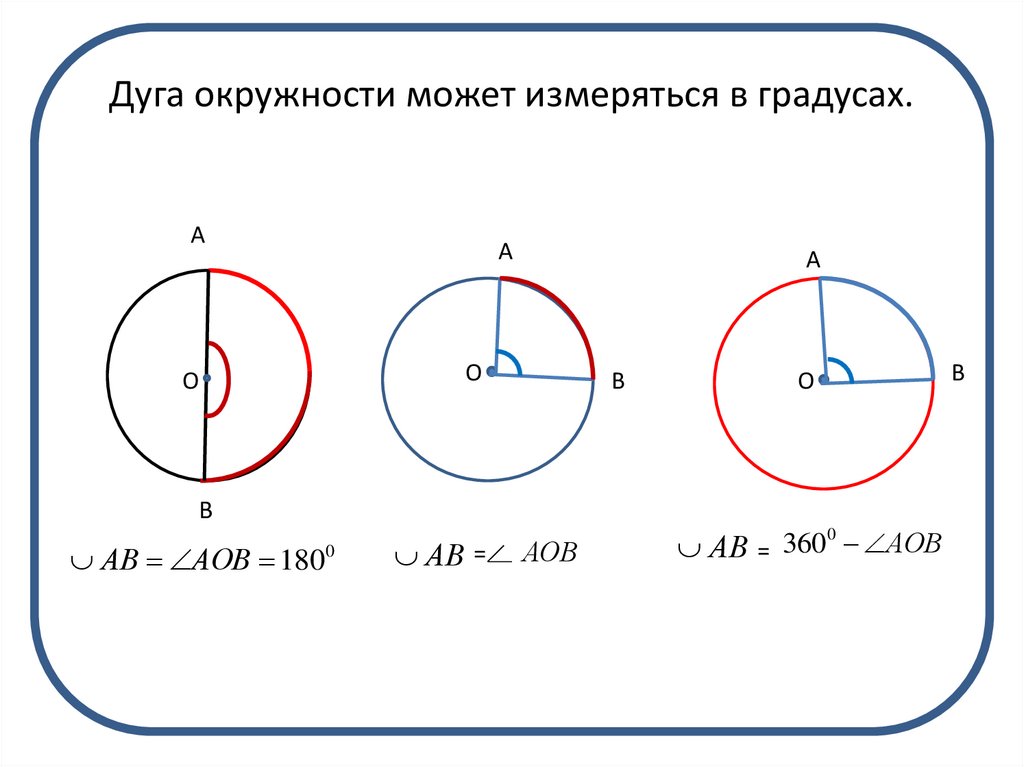
6. Дуга окружности может измеряться в градусах.
АА
А
О
О
В
В
АВ АОВ 180
0
АВ =
АОВ
О
0
АВ = 360 АОВ
В
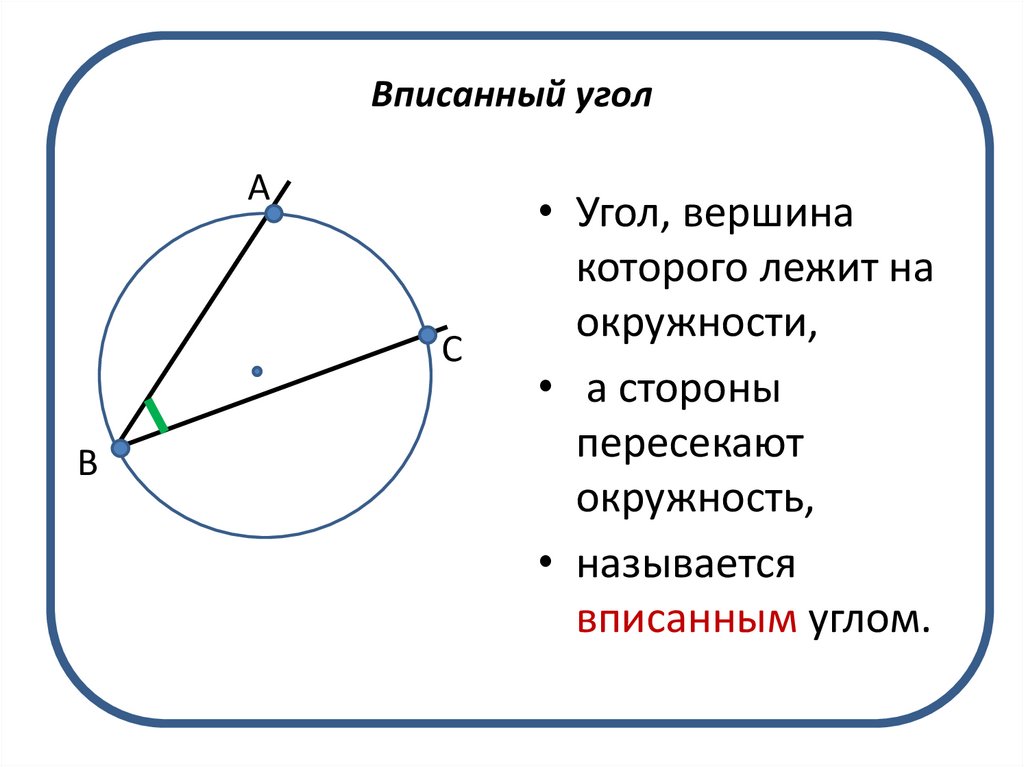
7. Вписанный угол
АС
В
• Угол, вершина
которого лежит на
окружности,
• а стороны
пересекают
окружность,
• называется
вписанным углом.
8.
АВАС- вписанный
ВМС- расположена
внутри этого угла.
С
О
Вписанный угол ВАС
опирается на дугу ВМС
В
М
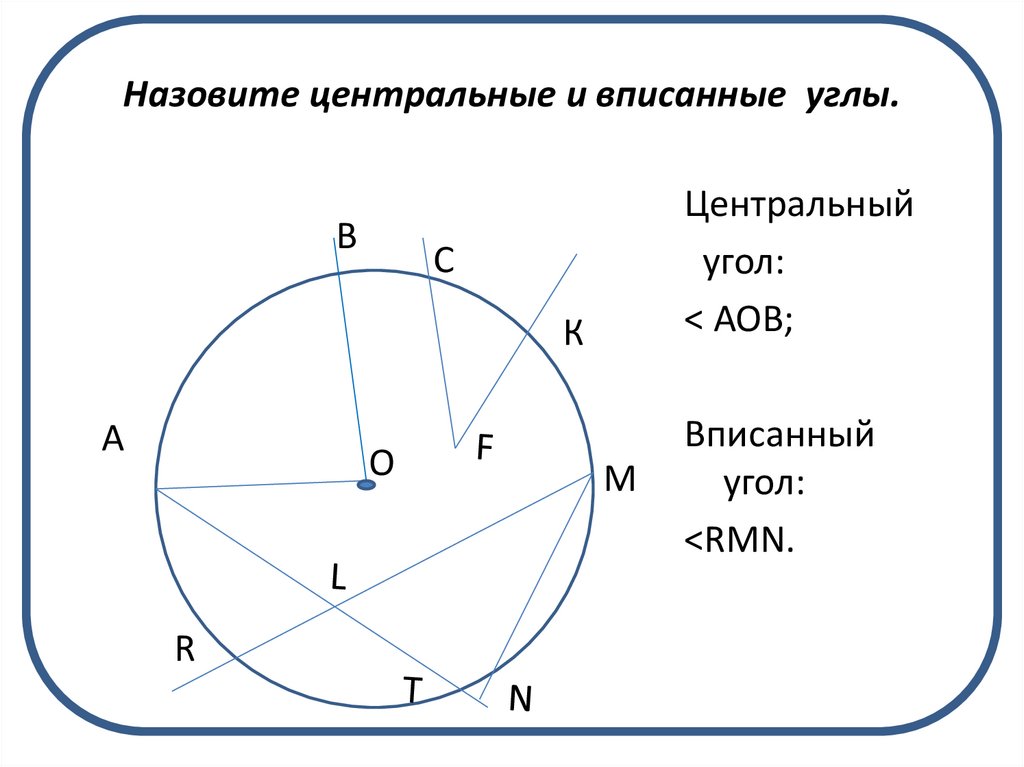
9. Назовите центральные и вписанные углы.
ВЦентральный
угол:
< АОВ;
С
К
А
О
R
М
Вписанный
угол:
<RMN.
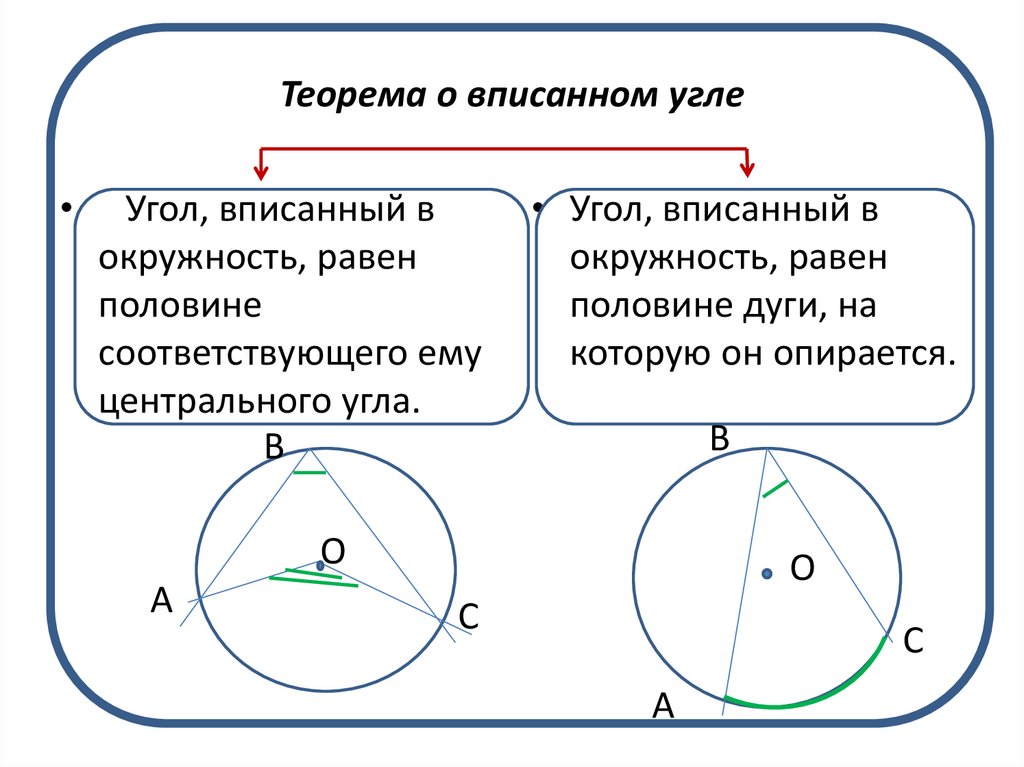
10. Теорема о вписанном угле
Угол, вписанный в
окружность, равен
половине
соответствующего ему
центрального угла.
В
• Угол, вписанный в
окружность, равен
половине дуги, на
которую он опирается.
В
О
А
О
С
С
А
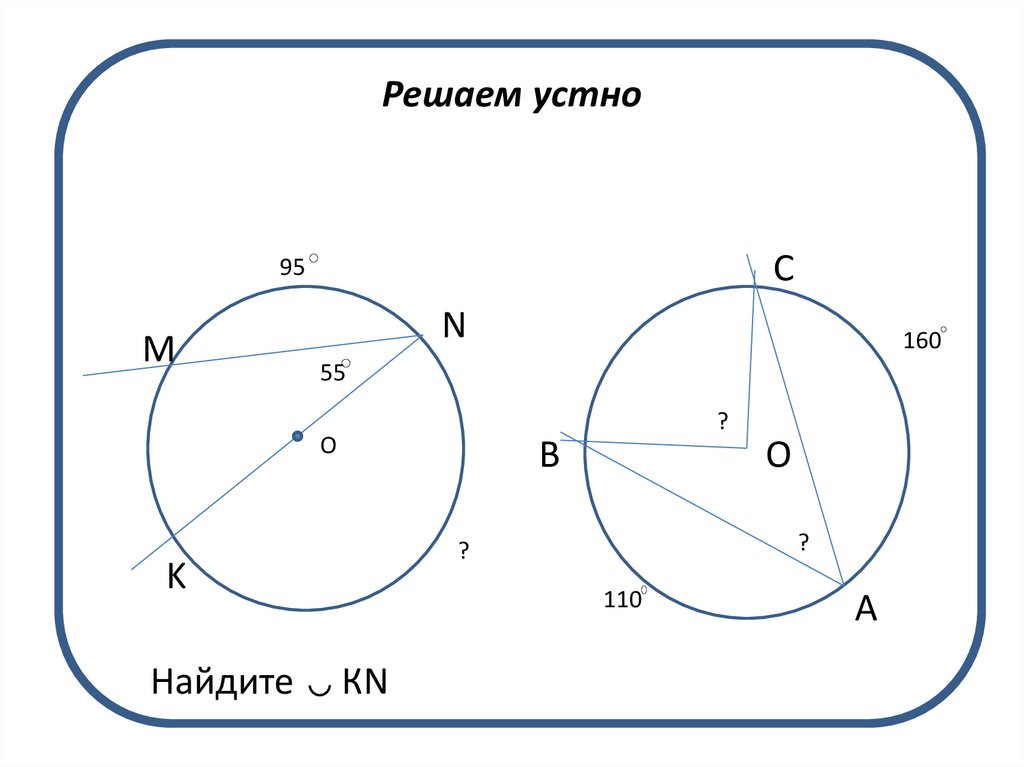
11. Решаем устно
С95
М
N
55
?
О
В
О
?
?
K
Найдите
160
110
КN
А
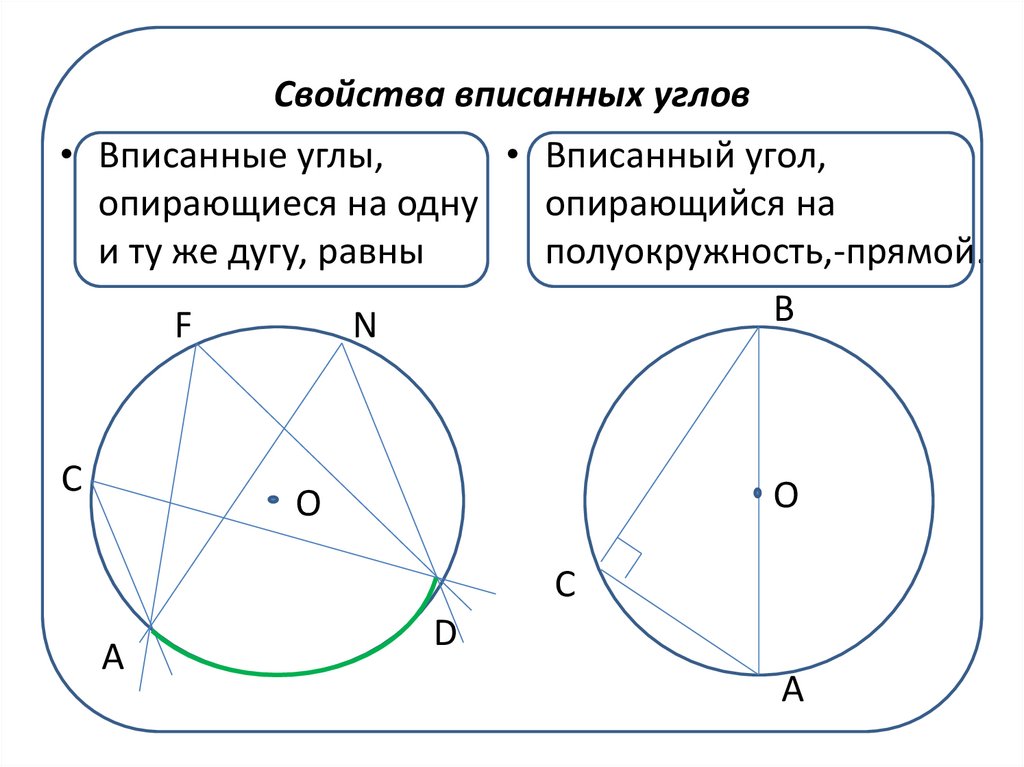
12. Свойства вписанных углов
• Вписанные углы,• Вписанный угол,
опирающиеся на одну
опирающийся на
и ту же дугу, равны
полуокружность,-прямой.
B
F
N
C
O
O
C
А
D
А
13. Решение задач
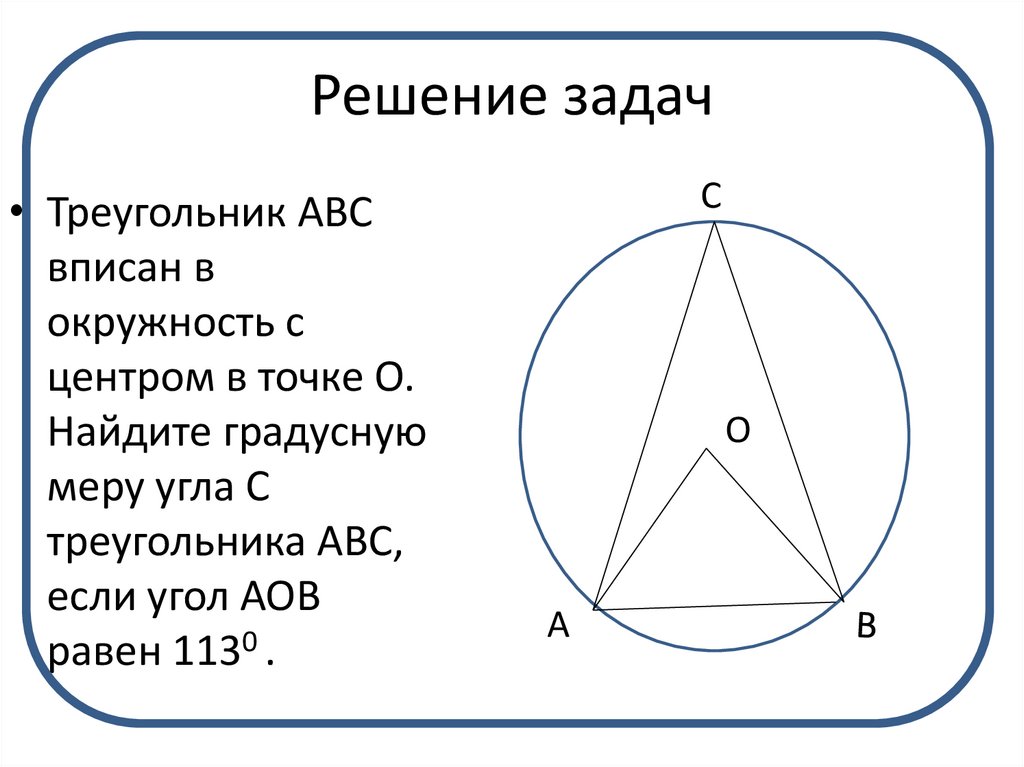
• Треугольник АВСвписан в
окружность с
центром в точке О.
Найдите градусную
меру угла С
треугольника АВС,
если угол АОВ
равен 1130 .
C
O
A
14. Решение задач
• В окружности с• АС и BD – диаметры
центром О, АС и ВD –
окружности с центром
диаметры.
О. Угол АСВ равен 790
Центральный угол АОD
Найдите угол АОD.
равен 1320 Найдите
Ответ дайте в
вписанный угол АСВ.
градусах.
Ответ дайте в
градусах.
15. Решение задач
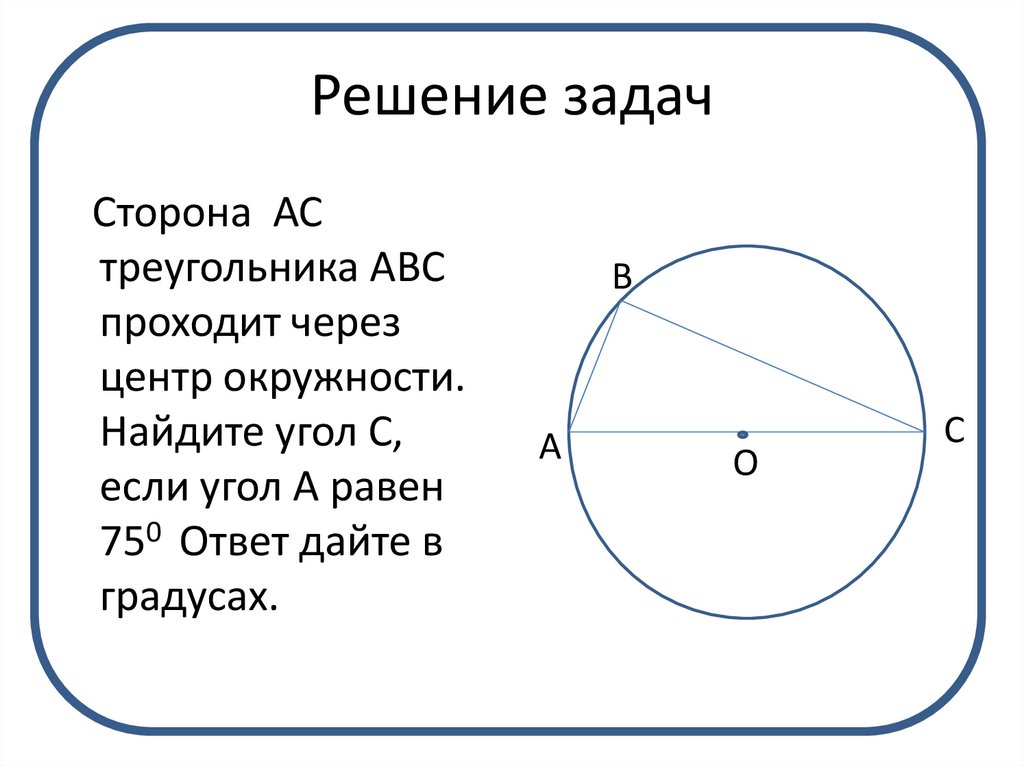
Сторона АСтреугольника АВС
проходит через
центр окружности.
Найдите угол С,
если угол А равен
750 Ответ дайте в
градусах.
В
А
О
С
16. Задание на дом
• Читать по учебнику п.70-71;• № 653(в,г); 654.
17. источники
• Геометрия 7-9 ,авторы: Л.С. Атанасян и др.,изд-во «Просвещение», 2013г.
• http://opengia.ru/subjects/mathematics9/topics/7
• "Презентация подготовлена на конкурс
"Радуга презентаций" для
международного сообщества педагогов "Я
- Учитель!""






 mathematics
mathematics








