Similar presentations:
Вписанные углы
1.
Тема урока:Вписанные углы
Ходина Н.В.
2. План урока:
1.2.
3.
4.
5.
6.
7.
8.
Повторение материала.
Знакомство с определением вписанного угла.
Доказательство теоремы, выражающей свойство
вписанного угла. (3 случая)
Формулировка двух следствий из теоремы.
Практическая работа.
Решение задач.
Итог урока.
Домашнее задание.
2
3.
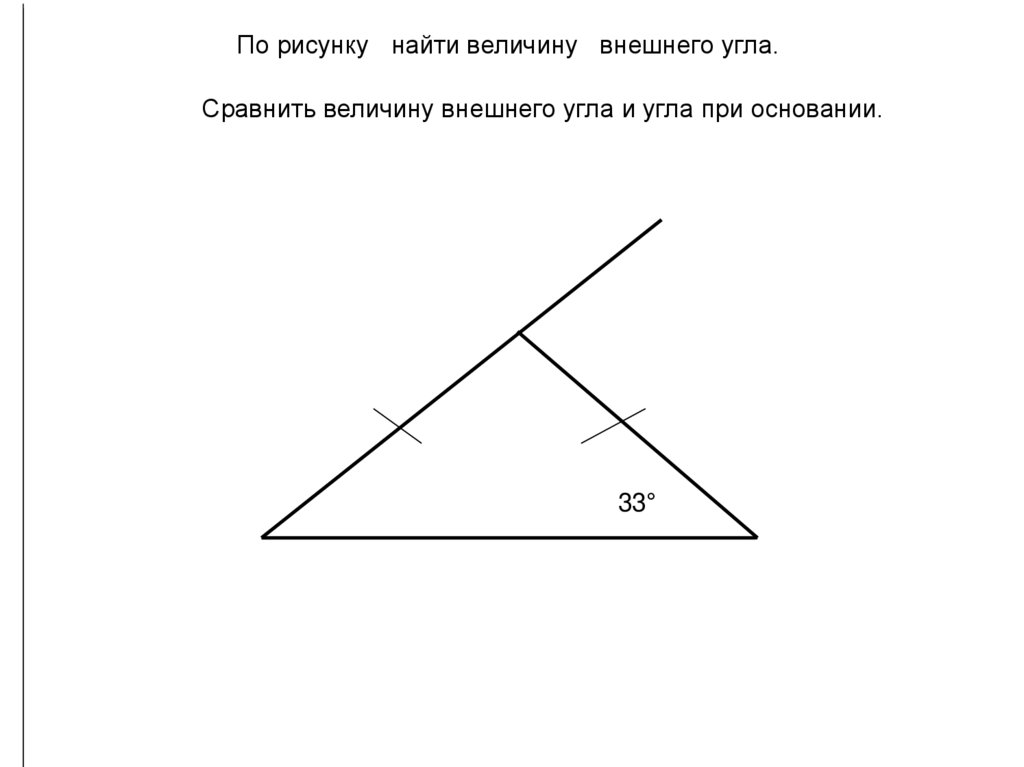
По рисунку найти величину внешнего угла.Сравнить величину внешнего угла и угла при основании.
33°
4. Угол, вершина которого совпадает с центром окружности называется ц е н р а л ь н ы м. Угол, вершина которого лежит на
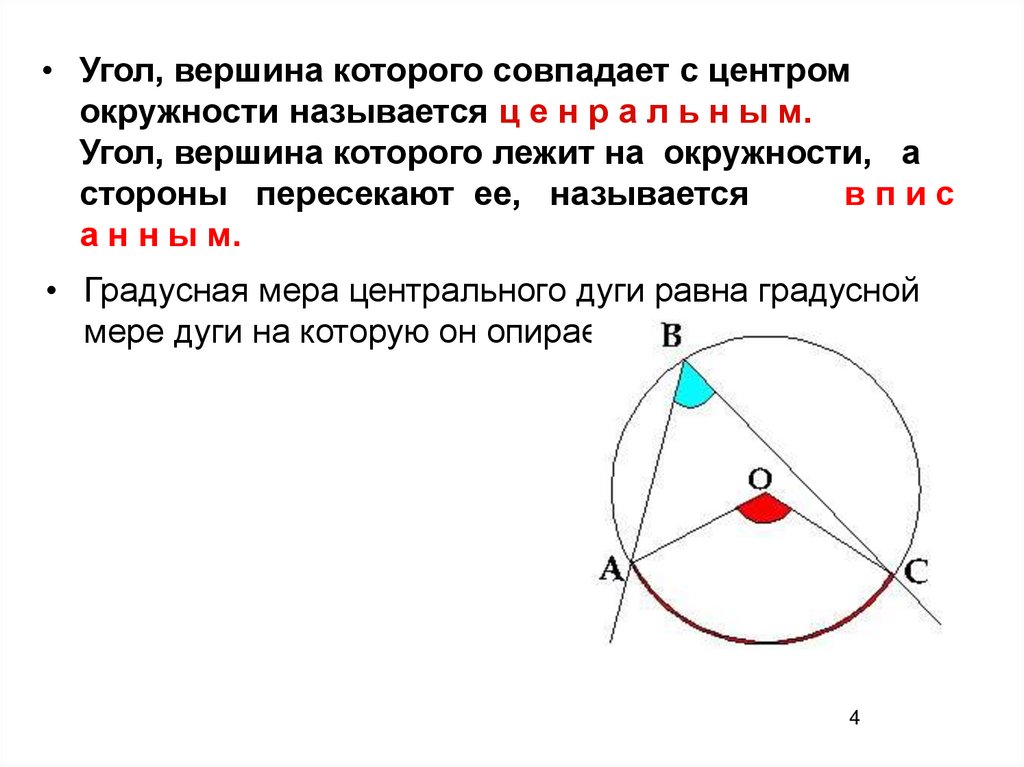
• Угол, вершина которого совпадает с центромокружности называется ц е н р а л ь н ы м.
Угол, вершина которого лежит на окружности, а
стороны пересекают ее, называется
впис
а н н ы м.
• Градусная мера центрального дуги равна градусной
мере дуги на которую он опирается .
4
5.
В чем разница между центральным ивписанным углами?
Угол, вершина которого совпадает с центром
окружности называется ценральным.
Угол, вершина которого лежит на окружности, а
стороны пересекают ее, называется
впис
а н н ы м.
6.
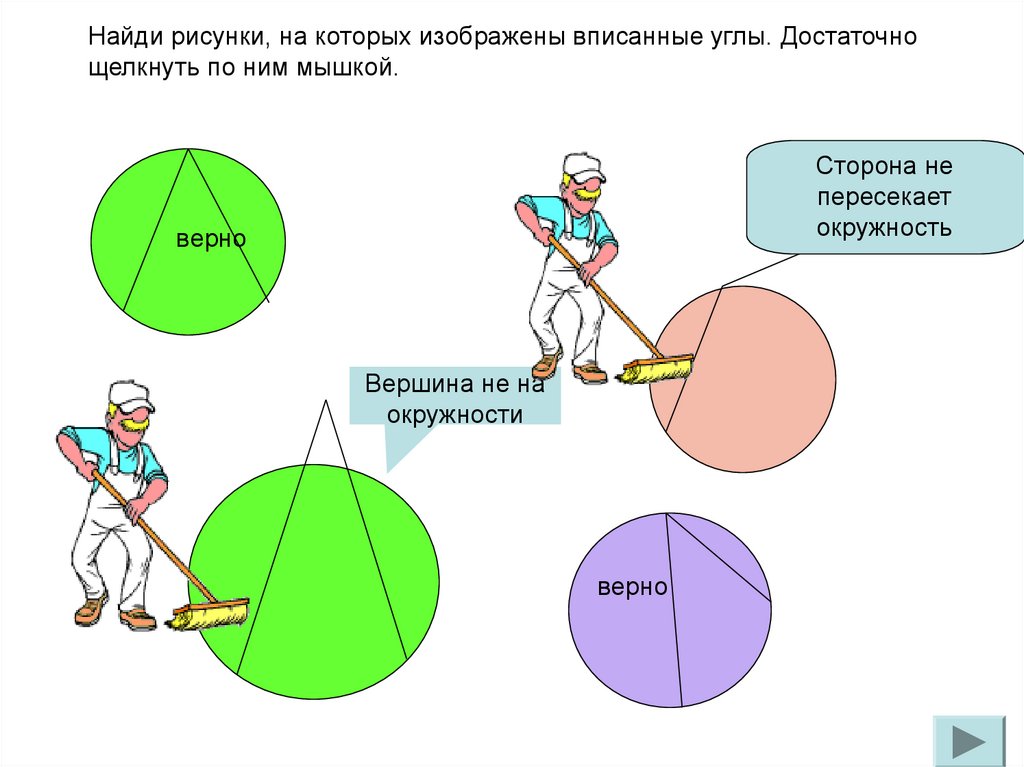
Найди рисунки, на которых изображены вписанные углы. Достаточнощелкнуть по ним мышкой.
Сторона не
пересекает
окружность
верно
Вершина не на
окружности
верно
7.
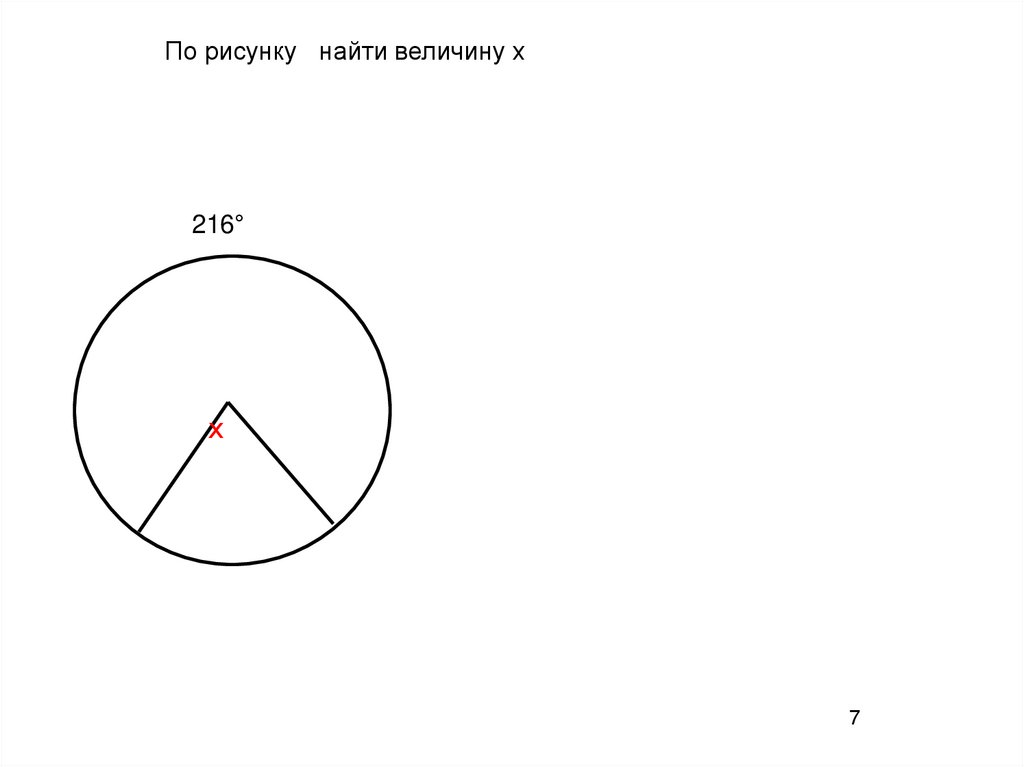
По рисунку найти величину х216°
х
7
8.
Задание:Выразить величину вписанного
угла,
зная, как выражается
величина центрального угла
через дугу, на которую он
опирается.
9.
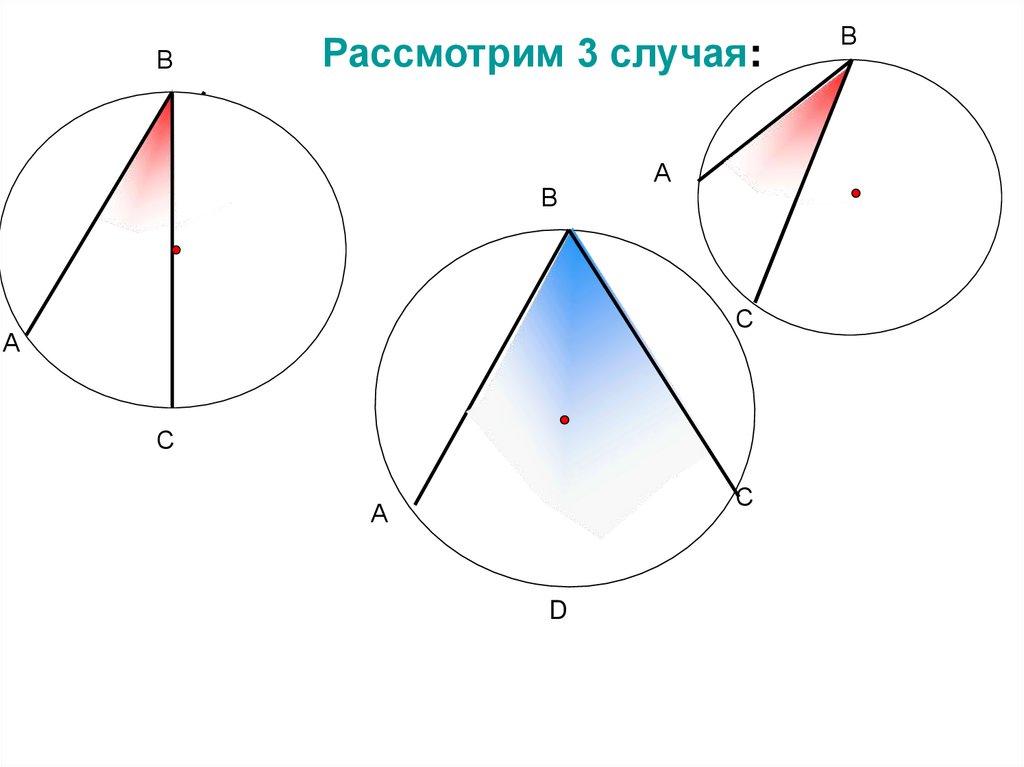
ВРассмотрим 3 случая:
В
А
С
А
С
С
А
D
В
10.
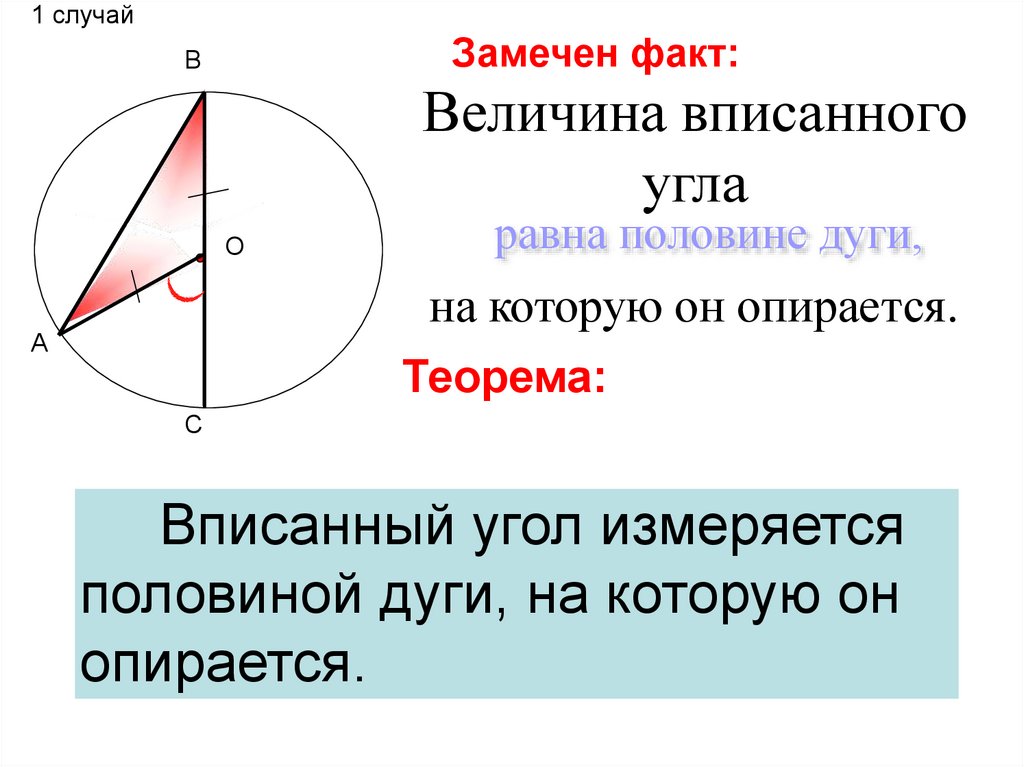
1 случайЗамечен факт:
В
Величина вписанного
угла
О
равна половине дуги,
на которую он опирается.
А
Теорема:
С
Вписанный угол измеряется
половиной дуги, на которую он
опирается.
11.
ВДано:
1
О
2
Док-ть:
Доказательство:
А
С
12.
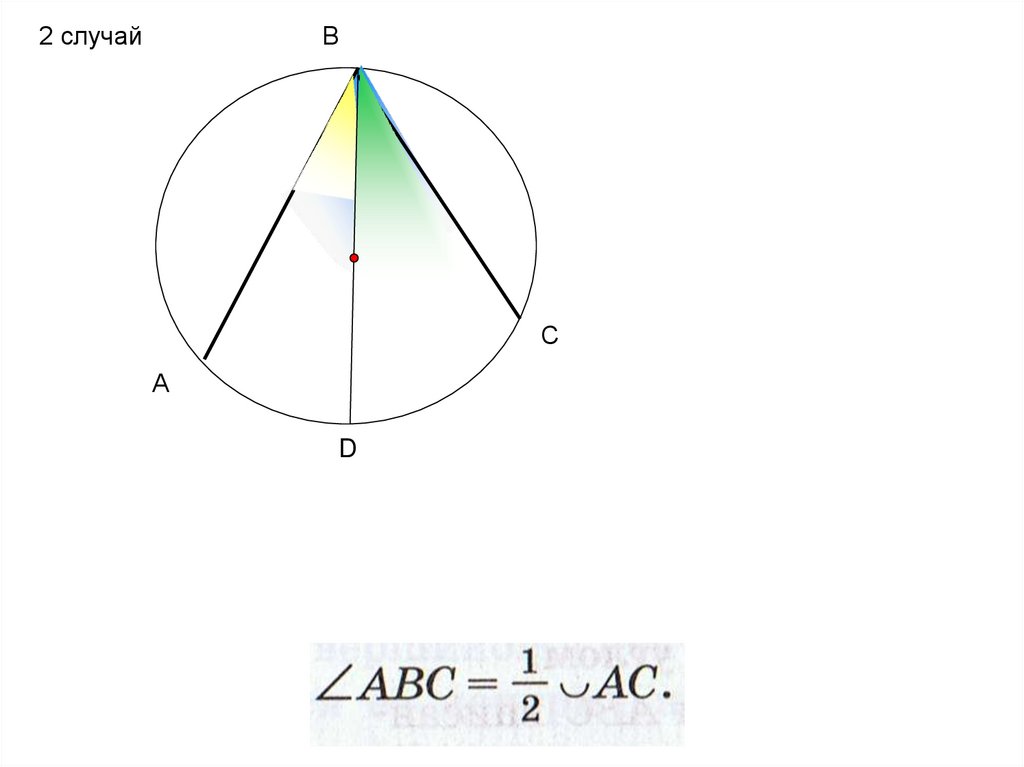
2 случайВ
С
А
D
13.
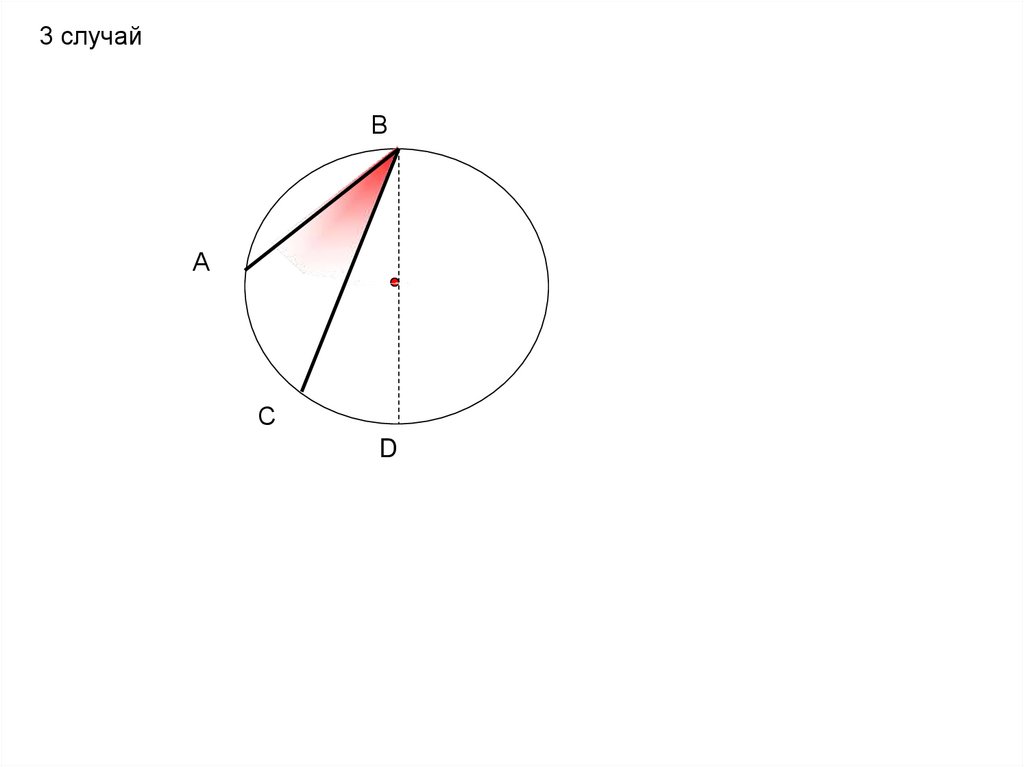
3 случайВ
А
С
D
14.
Проблема№
1:
Как быстро циркулем и
линейкой
построить сразу несколько углов
равных данному ?
15.
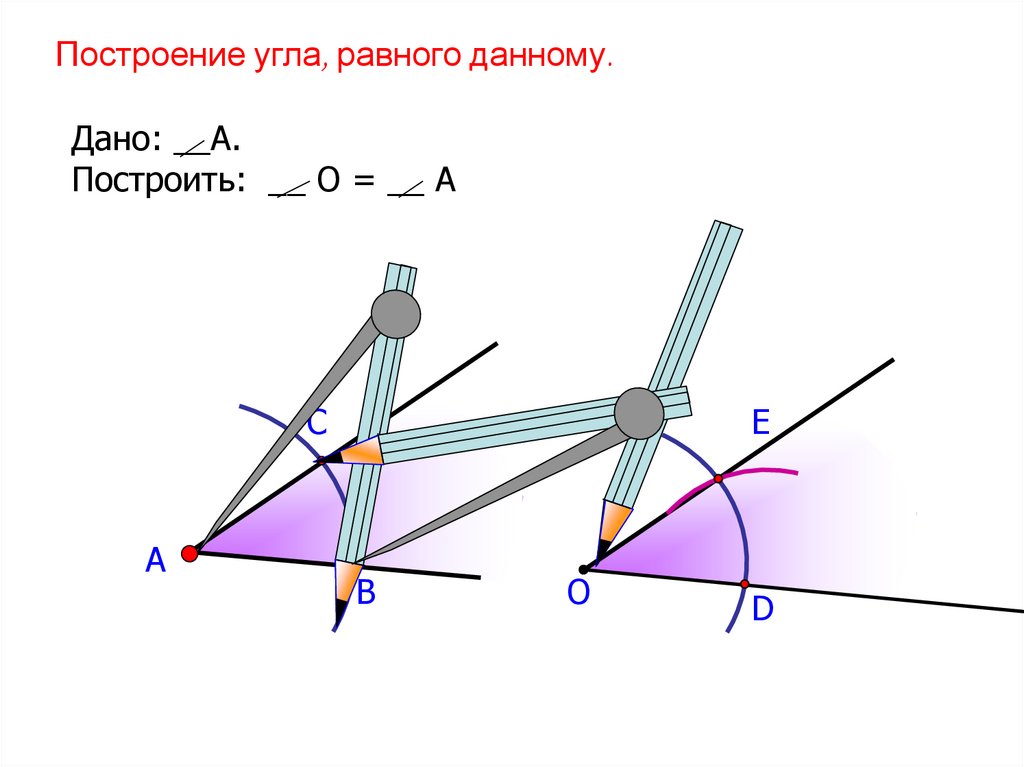
Построение угла, равного данному.Дано: __А.
Построить: __ О = __ А
С
А
E
В
О
D
16.
Проблема №1:
Быстро!
Сразу
Не
неско
решено!
лько!
17.
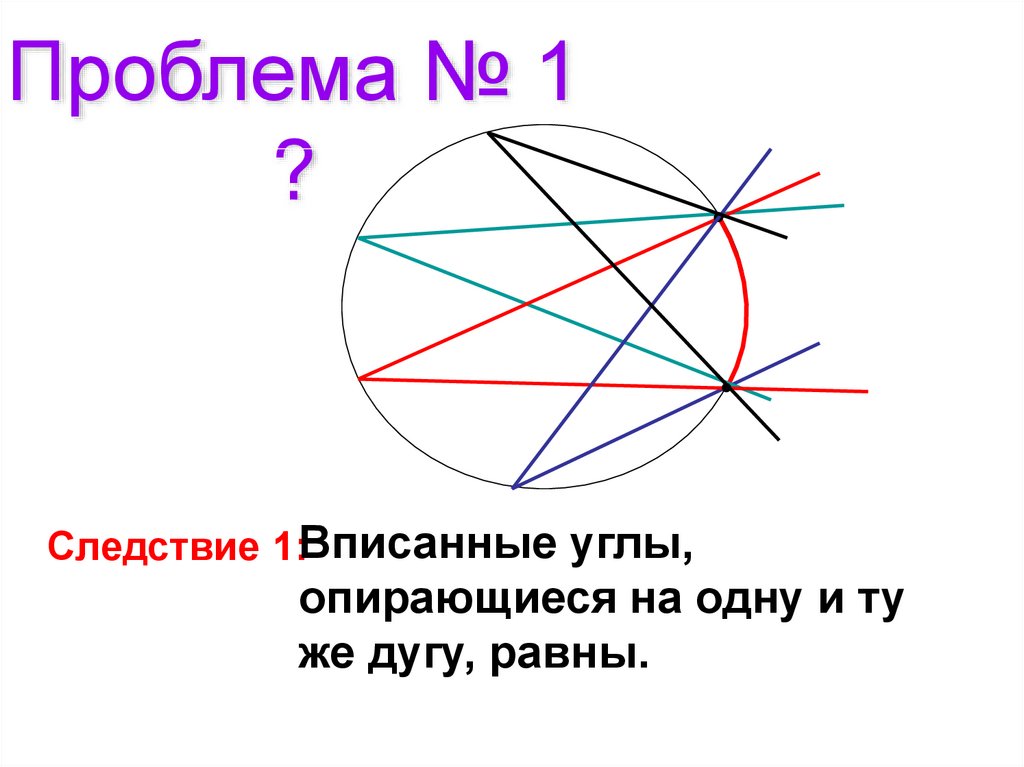
Проблема № 1?
Следствие 1:Вписанные углы,
опирающиеся на одну и ту
же дугу, равны.
18.
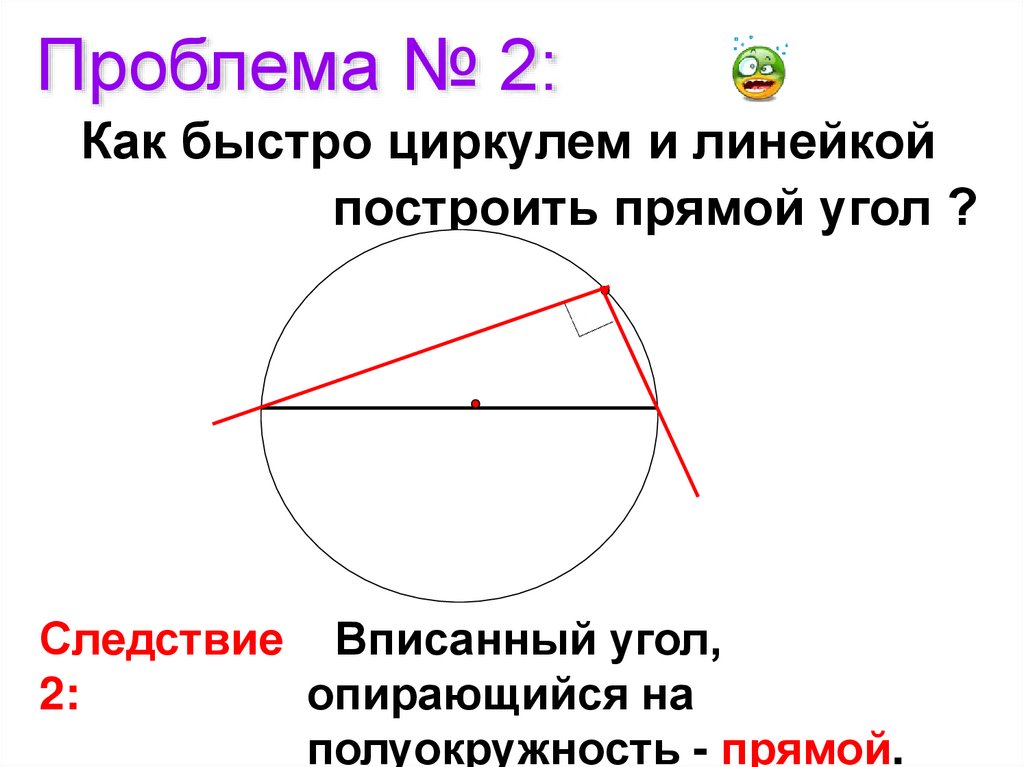
Проблема № 2:Как быстро циркулем и линейкой
построить прямой угол ?
19.
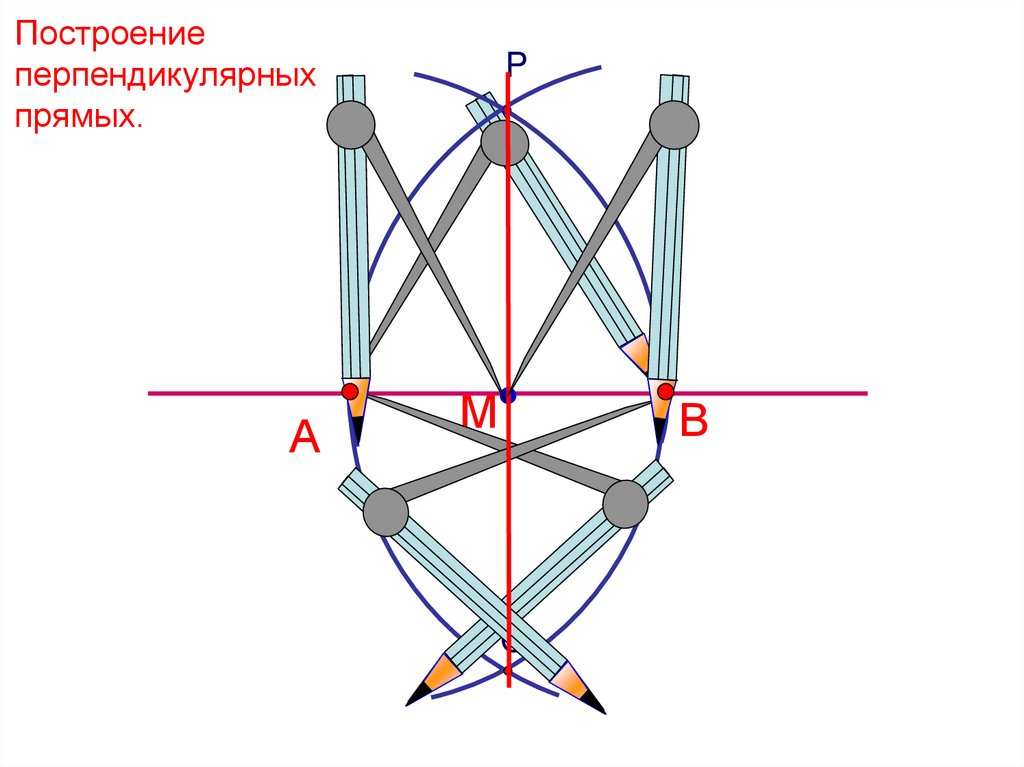
Построениеперпендикулярных
прямых.
А
P
М
В
Q
20.
Проблема № 2:Как быстро циркулем и линейкой
построить прямой угол ?
Следствие Вписанный угол,
2:
опирающийся на
полуокружность - прямой.
21.
Практическая работа22.
23.
24.
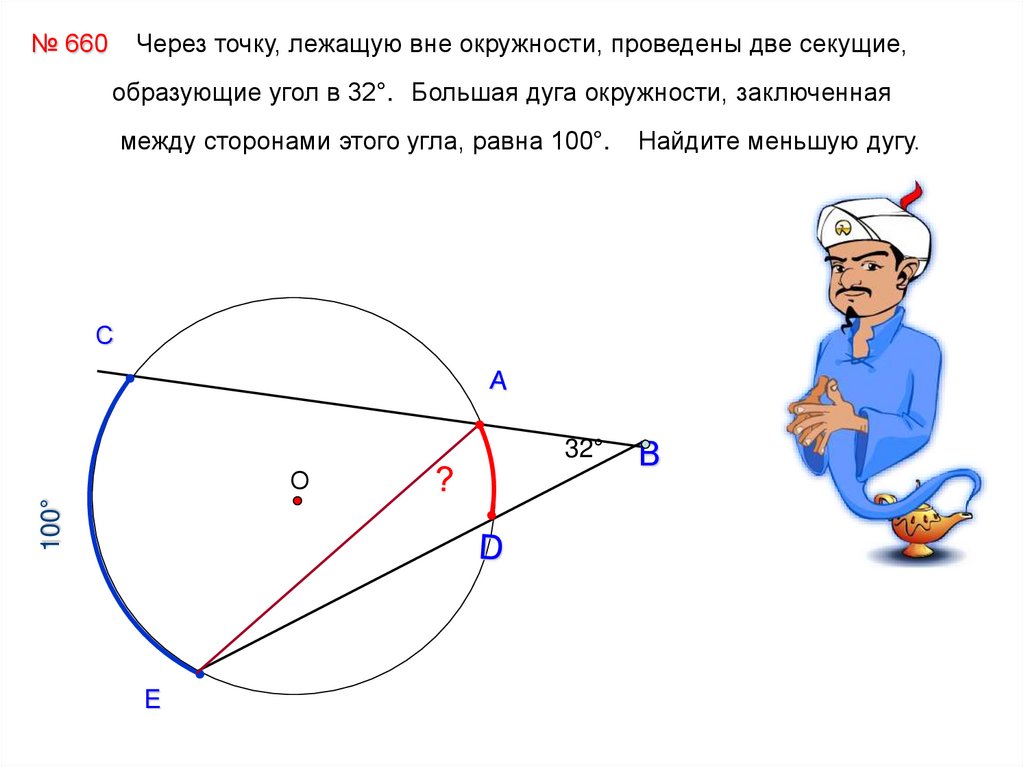
№ 660Через точку, лежащую вне окружности, проведены две секущие,
образующие угол в 32°. Большая дуга окружности, заключенная
между сторонами этого угла, равна 100°.
Найдите меньшую дугу.
С
32°
100°
О
E
В
25.
26.
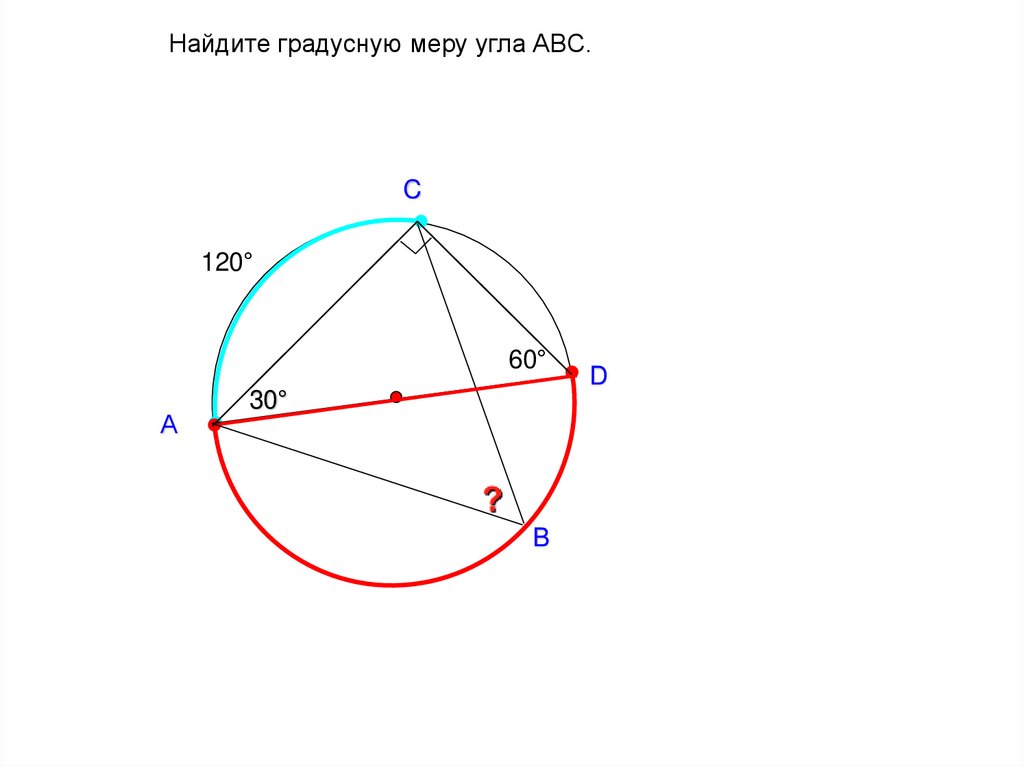
Найдите градусную меру угла ABC.C
120°
60°
А
30°
B
D
27.
28.
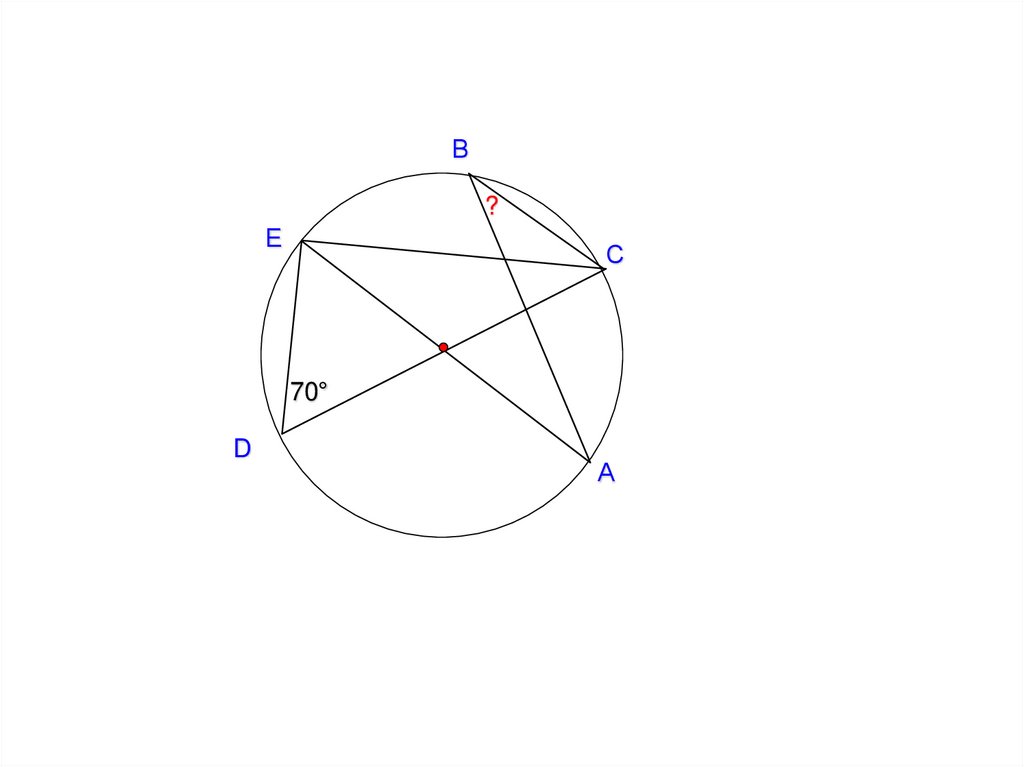
В?
Е
С
70°
D
А
29.
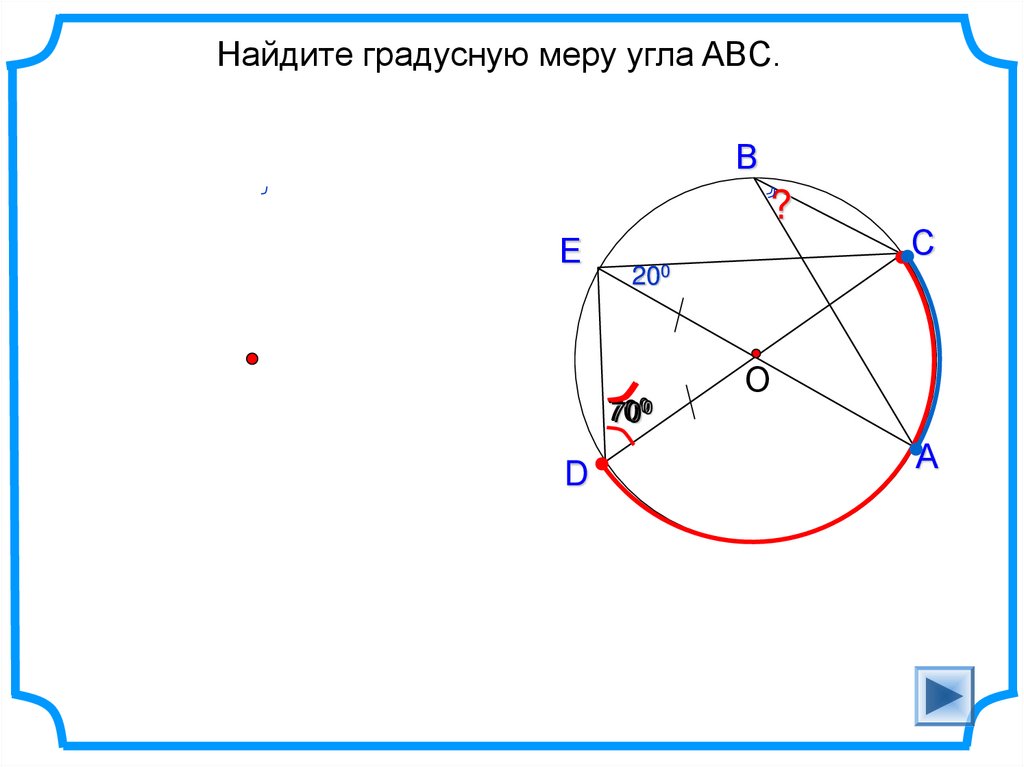
Найдите градусную меру угла ABC.В
?
Е
200
70
7000
D
С
О
А
30.
Итог урока:Найди ошибку в формулировках:
1. Вписанным называется угол,
вершина которого лежит на окружности.
2. Вписанный угол измеряется величиной
дуги, на которую он опирается.
Закончи фразу:
1. Вписанные углы равны, если…
2. Вписанный угол прямой, если…
31. Домашнее задание:
п.71, выучитьопределения центрального вписанного углов,
теорему о вписанном угле, (записать док-во 2
и 3 случаев и двух следствий из нее)
№657- выполнить письменно,
№654-устно














 mathematics
mathematics








