Структурные схемы, типовые соединения звеньев. Линейные системы

1.

Теория автоматического управления
СТРУКТУРНЫЕ СХЕМЫ, ТИПОВЫЕ
СОЕДИНЕНИЯ ЗВЕНЬЕВ
«Линейные
системы»
лекция 6,7

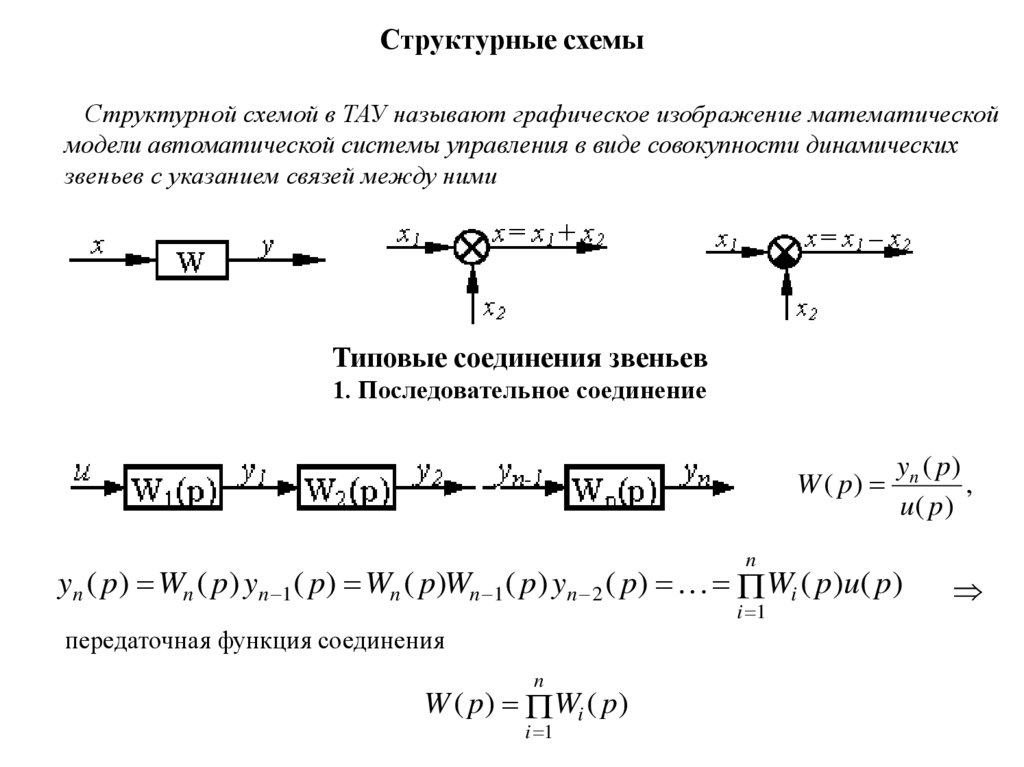
2. Структурные схемы

Структурной схемой в ТАУ называют графическое изображение математической
модели автоматической системы управления в виде совокупности динамических
звеньев с указанием связей между ними
Типовые соединения звеньев
1. Последовательное соединение
W ( p)
n
yn ( p )
,
u( p )
yn ( p) Wn ( p) yn 1 ( p) Wn ( p)Wn 1 ( p) yn 2 ( p) Wi ( p)u( p)
i 1
передаточная функция соединения
n
W ( p) Wi ( p)
i 1

3.

n
W ( j ) Wi ( j )
Комплексный коэффициент усиления соединения
i 1
n
A( )e j ( ) Ai ( )e j i ( )
i 1
n
АЧХ
A( ) Ai ( )
ФЧХ
( ) i ( )
i 1
n
i 1
ЛАЧХ
n
20 lg A( ) 20 lg Ai ( )
i 1
n
L( ) Li ( )
i 1
Правило. построения асимптотическую ЛАЧХ по передаточной функции
W ( p)
где
Ti , T j
k Ti p 1
i
j
Tj p 1
,
- положительные постоянные времени

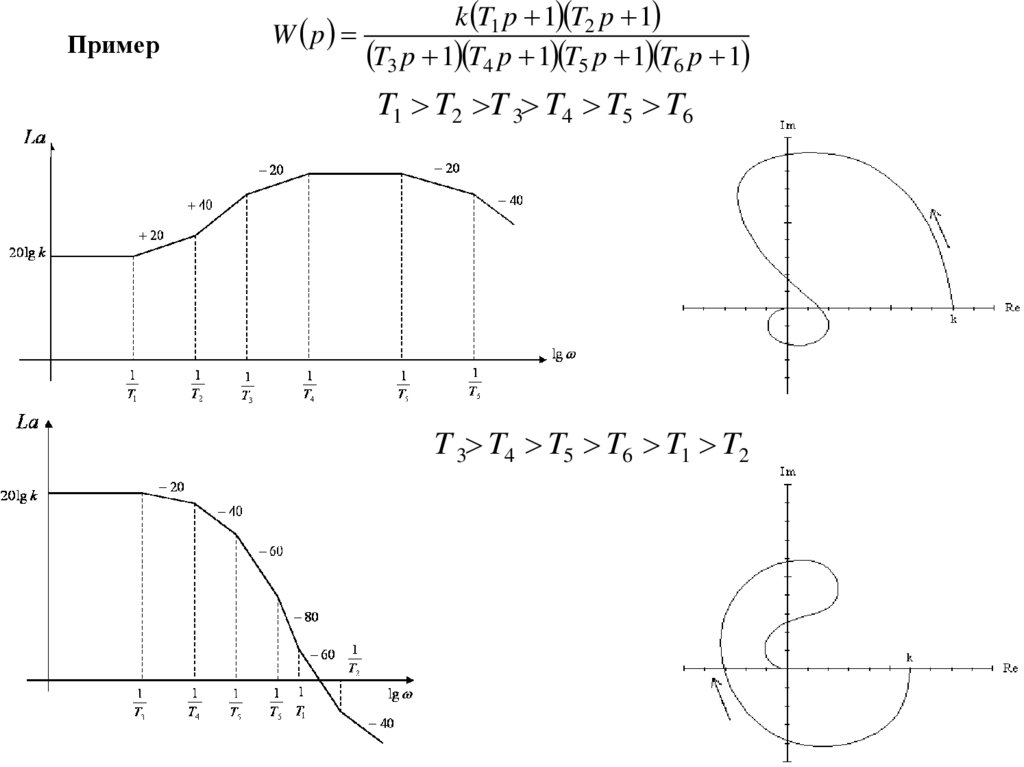
4.

Пример
W p
k T1 p 1 T2 p 1
T3 p 1 T4 p 1 T5 p 1 T6 p 1
T1 T2 T 3 T4 T5 T6
T 3 T4 T5 T6 T1 T2

5.

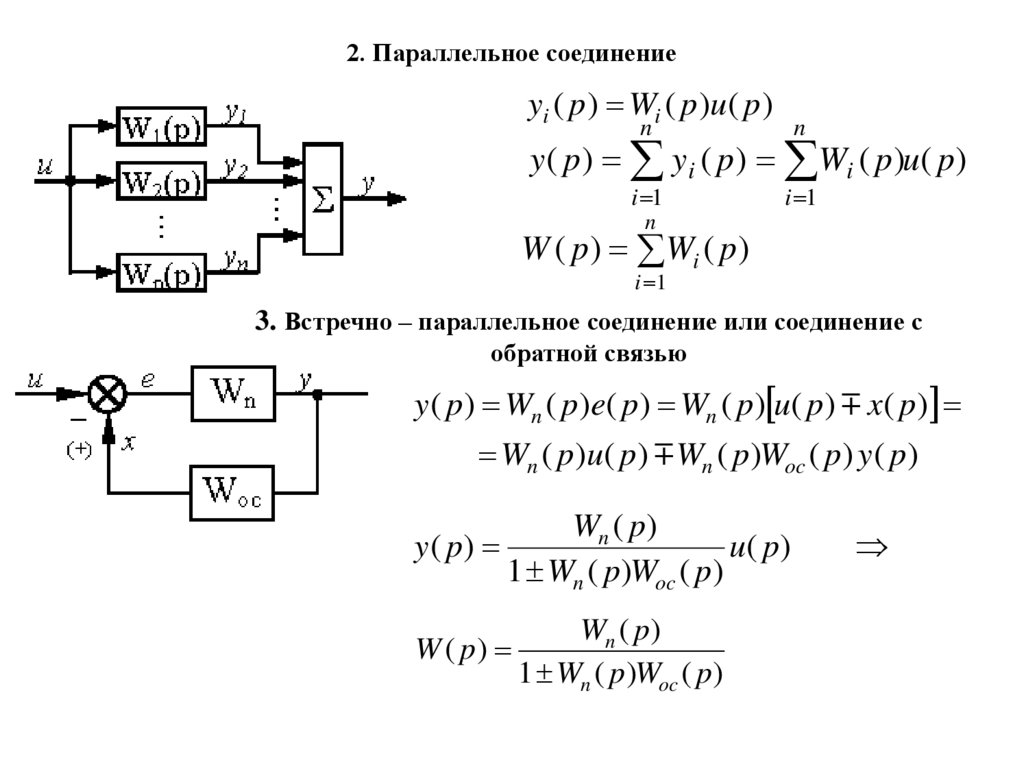
2. Параллельное соединение
yi ( p ) Wi ( p )u( p )
n
n
i 1
i 1
y ( p ) y i ( p ) Wi ( p )u( p )
n
W ( p ) Wi ( p )
i 1
3. Встречно – параллельное соединение или соединение с
обратной связью
y ( p) Wn ( p)e( p) Wn ( p) u( p) x( p)
Wn ( p)u( p) Wn ( p)Woc ( p) y ( p)
y( p)
Wn ( p )
u( p )
1 Wn ( p )Woc ( p )
W ( p)
Wn ( p )
1 Wn ( p )Woc ( p )

6.

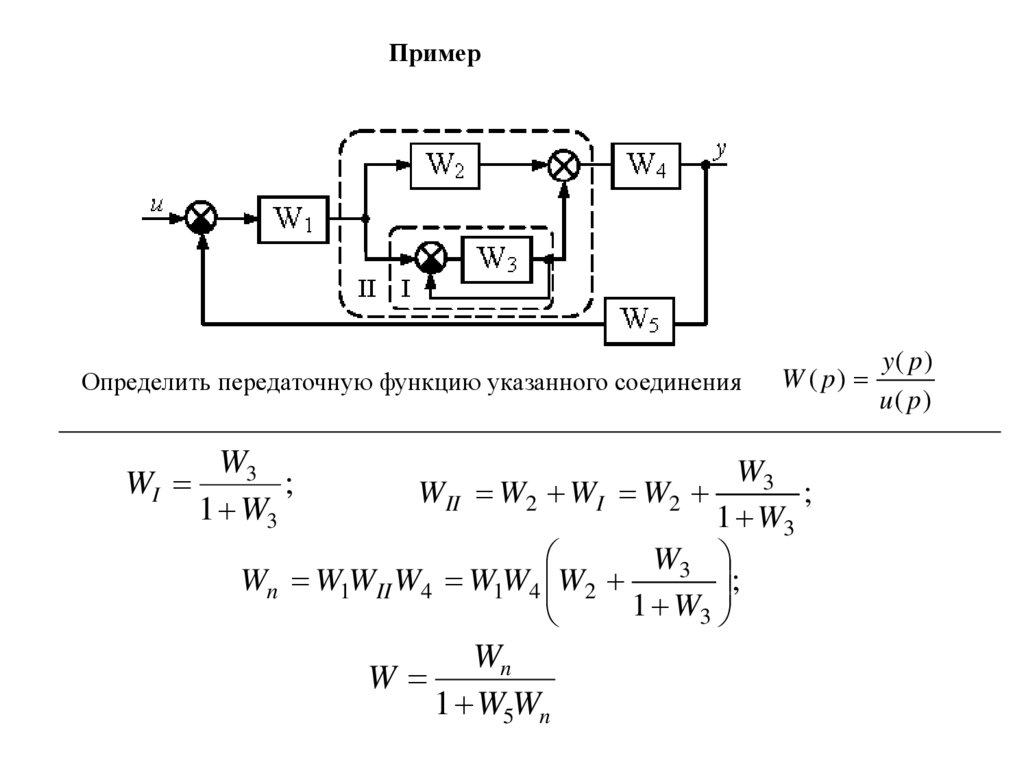
Пример
Определить передаточную функцию указанного соединения
WI
W3
;
1 W3
W ( p)
W3
WII W2 WI W2
;
1 W3
W3
;
Wn W1WII W4 W1W4 W2
1 W3
W
Wn
1 W5Wn
y( p)
u( p )

7.

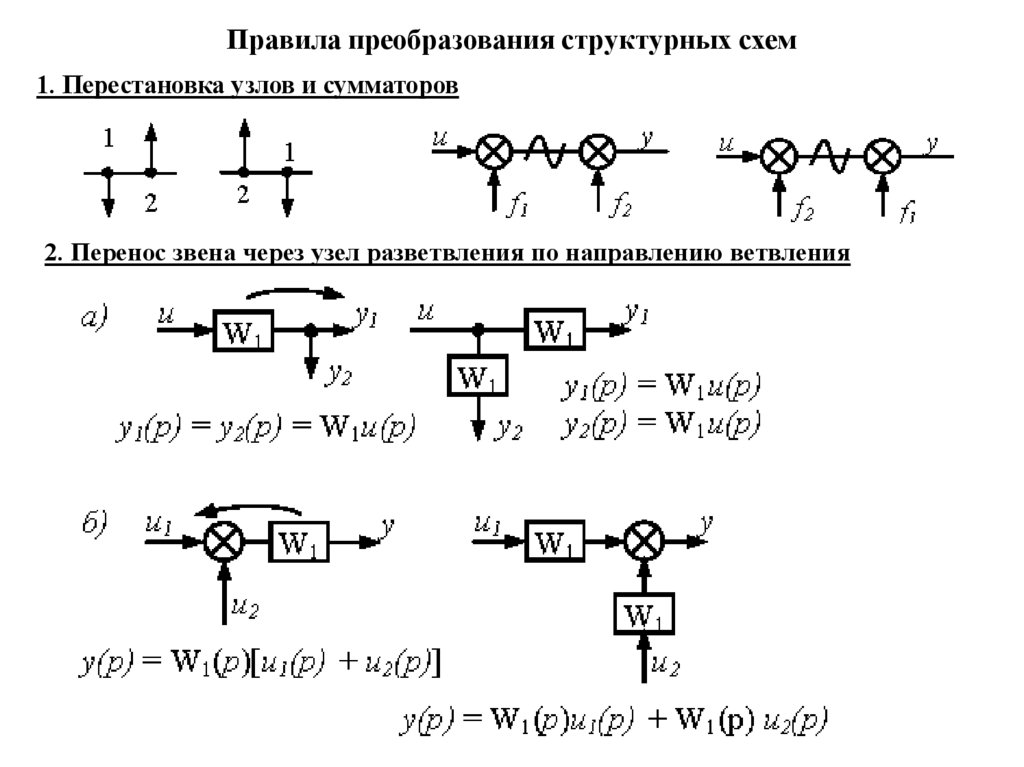
Правила преобразования структурных схем
1. Перестановка узлов и сумматоров
2. Перенос звена через узел разветвления по направлению ветвления

8.

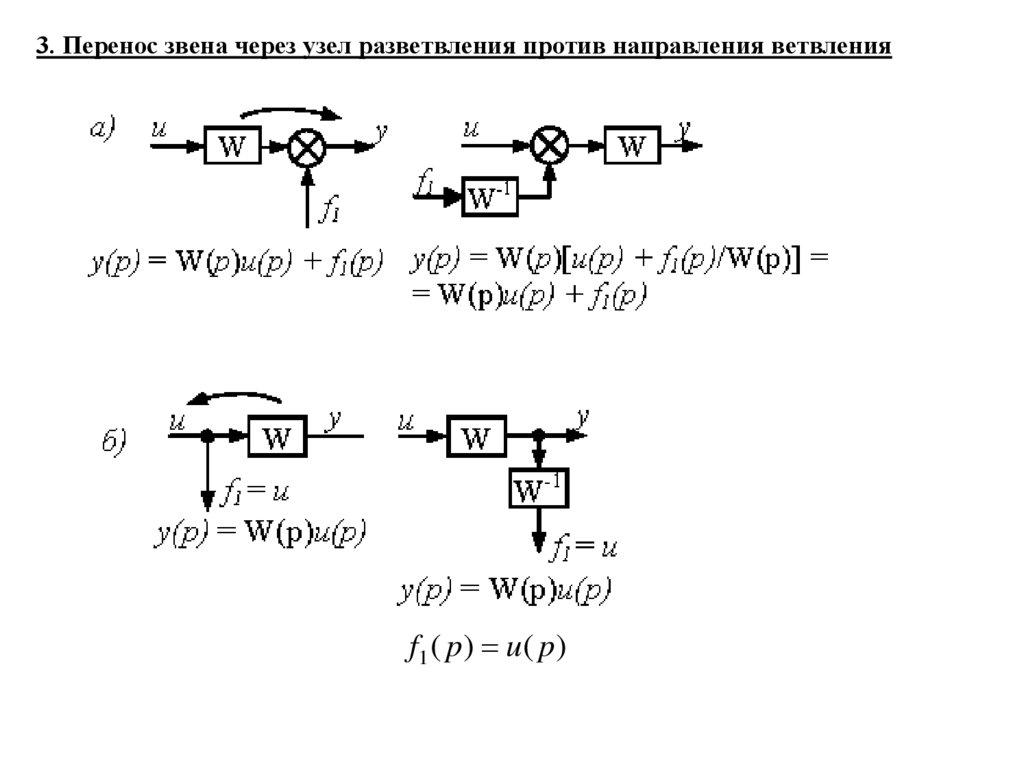
3. Перенос звена через узел разветвления против направления ветвления
f1 ( p ) u ( p )

9.

10.

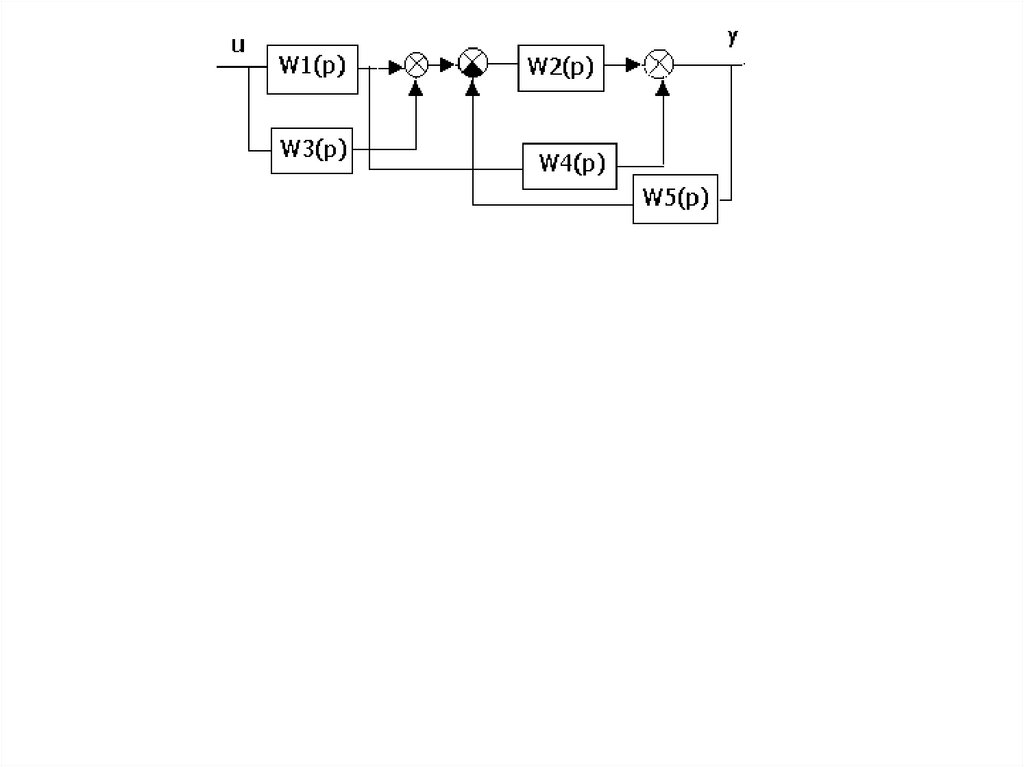
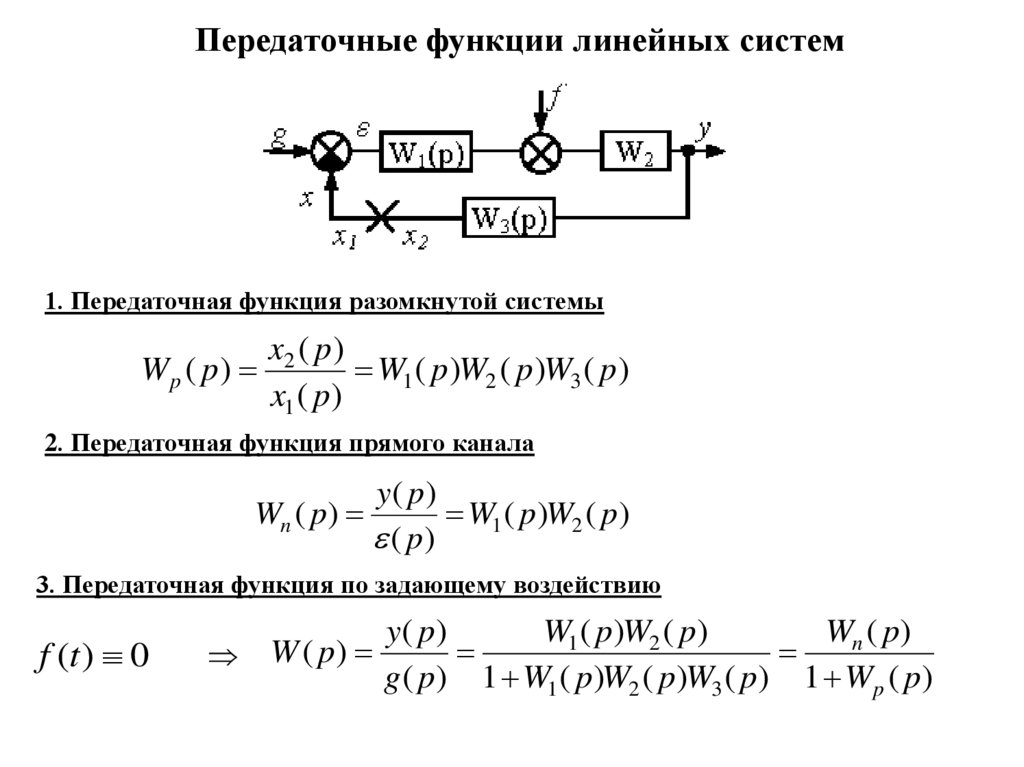
Передаточные функции линейных систем
1. Передаточная функция разомкнутой системы
Wp ( p)
x2 ( p )
W1 ( p )W2 ( p )W3 ( p )
x1 ( p )
2. Передаточная функция прямого канала
y ( p)
Wn ( p)
W1 ( p)W2 ( p)
( p)
3. Передаточная функция по задающему воздействию
f (t ) 0
y ( p)
W1 ( p)W2 ( p)
Wn ( p)
W ( p)
g ( p) 1 W1 ( p)W2 ( p)W3 ( p) 1 Wp ( p)

11.

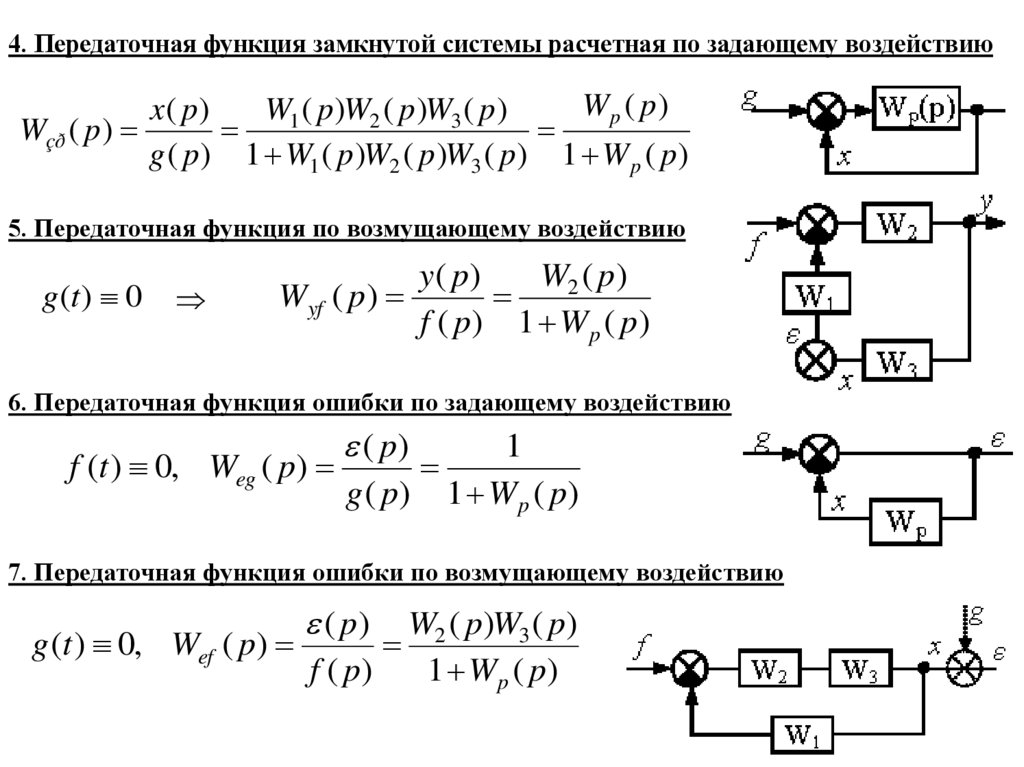
4. Передаточная функция замкнутой системы расчетная по задающему воздействию
Wp ( p)
x( p)
W1 ( p )W2 ( p )W3 ( p )
Wçð ( p )
g ( p ) 1 W1 ( p )W2 ( p )W3 ( p ) 1 W p ( p )
5. Передаточная функция по возмущающему воздействию
g (t ) 0
y ( p)
W2 ( p)
Wyf ( p)
f ( p) 1 Wp ( p)
6. Передаточная функция ошибки по задающему воздействию
f (t ) 0, Weg ( p)
( p)
g ( p)
1
1 Wp ( p)
7. Передаточная функция ошибки по возмущающему воздействию
g (t ) 0, Wef ( p)
( p)
f ( p)
W2 ( p)W3 ( p)
1 Wp ( p)

12.

Статические и астатические системы и их
характеристики
R p
Wp p v
,
p Q p
Z
Необходимо определить, чему равна ошибка в установившемся состоянии при подаче
на вход системы единичного ступенчатого воздействия:
ycm lim t ,
t
g (t ) 1(t )
Воспользуемся следствием из теоремы о производной функции :
p Weg p g p ,
1
L 1(t )
p
lim t lim p p
t
óñò
1
1
p Q p
lim pWeg p g p lim p
lim
,
p 0
p 0 1 W p p
p 0 p Q p R p
p
óñò
0,
const ,
0,
0
Если уст 0 , а равна постоянной величине , то система называется
статической, S – коэффициентом статизма.
g t 1 t
если
уст aS
Если же ошибка в установившемся состоянии при подаче на вход единичного
ступенчатого воздействия равна 0, то система называется астатической.
p 0

13.

Признаки астатизма
1.Если в разомкнутой системе имеется интегрирующее звено, то замкнутая система
будет астатической.
2. Если
lim Wçð p 1
, система астатическая
p 0
Wp
R p
,
p Q p
Wp p
x p
R p
Wçð p
g p 1 W p p p Q p R p
lim Wçð p lim
p 0
где
p 0
R p
1
p Q p R p
показатель или порядок астатизма

14.

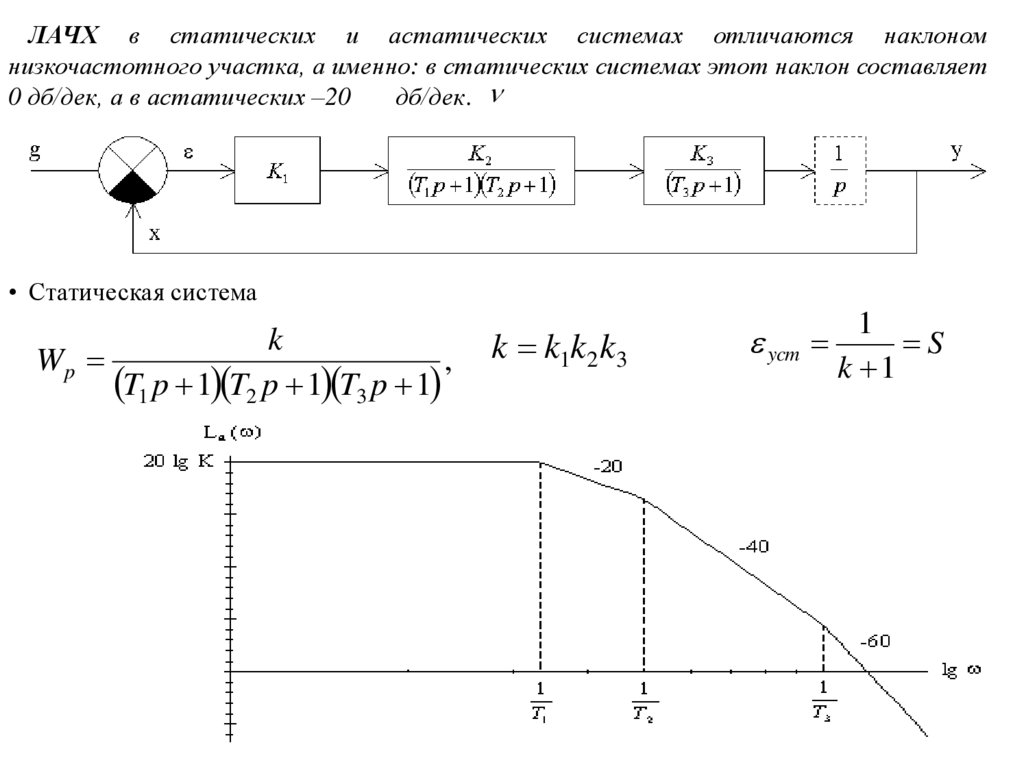
ЛАЧХ в статических и астатических системах отличаются наклоном
низкочастотного участка, а именно: в статических системах этот наклон составляет
0 дб/дек, а в астатических –20
дб/дек.
• Статическая система
k
Wp
,
T1 p 1 T2 p 1 T3 p 1
k k1k2 k3
ycm
1
S
k 1

15.

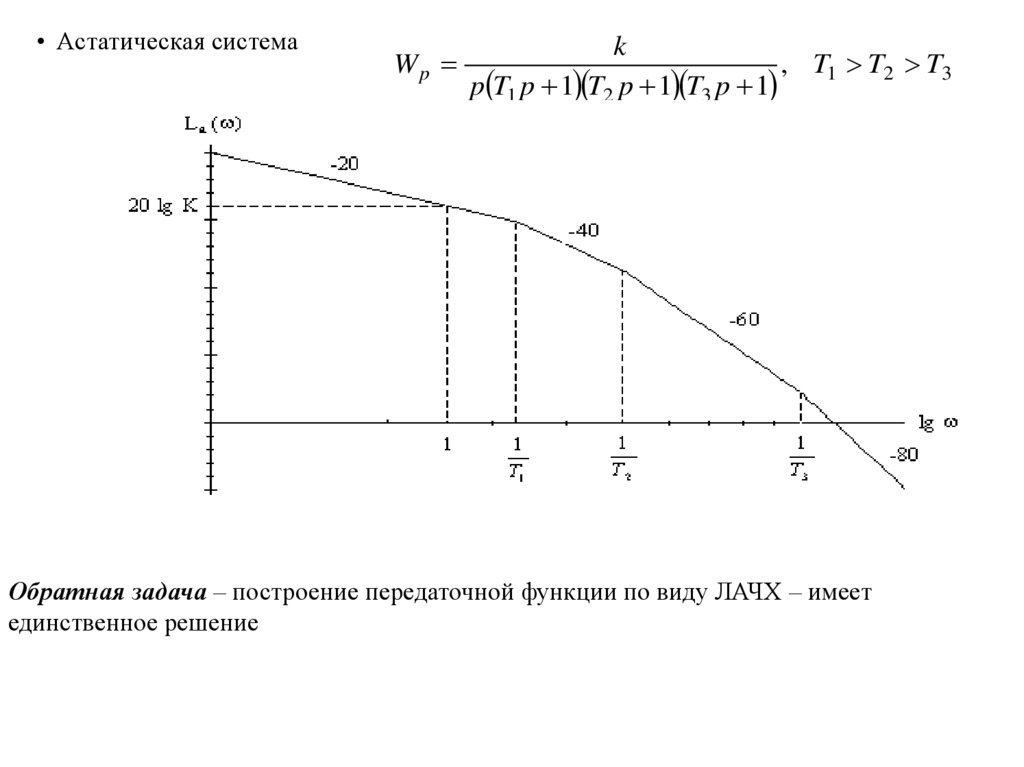
• Астатическая система
k
Wp
, T1 T2 T3
p T1 p 1 T2 p 1 T3 p 1
Обратная задача – построение передаточной функции по виду ЛАЧХ – имеет
единственное решение

16.

Годографы статических и астатических систем
Годограф статической системы всегда начинается с
точки k на вещественной оси
k
Wp
T1 p 1 T2 p 1 T3 p 1
В астатической системе присутствие интегрирующего
звена определяет начальный сдвиг фаз
W p
1,
0
2,
0
k
p v T1 p 1 T2 p 1 T3 p 1
2
3,
0
3
2